绿泥石片岩隧洞大变形特征及控制措施——以滇中引水工程香炉山隧洞为例

刘海明，成远登，吴永红，张雨霆，丁文云，王忠伟

(1.昆明理工大学 建筑工程学院，昆明 650500； 2.长江科学院 水利部岩土力学与工程重点实验室，武汉 430010； 3.中铁二院昆明勘察设计研究院有限责任公司，昆明 650500； 4.保(山)施(甸)高速公路投资开发责任公司，云南 保山 678200)

1 研究背景

滇中引水工程规模大、线路长、地质条件复杂，存在活动断层、高地应力、软岩大变形等重大工程地质问题，其工程规模和工程技术难度均居世界前列[1]。该工程隧洞中绿泥石片岩具有结构松散，节理发育，强度低等特点，属于典型的软岩[2]。如连城山隧道在穿越典型的绿泥石片岩地层时曾发生严重的大变形灾害[2-3]。隧道开挖初期支护施作后，受绿泥石片岩岩体状态的影响，围岩最大变形速率达到31.4 cm/d，累计变形340 cm，严重影响了隧道结构的安全性，需经常换拱处理控制大变形。此外，锦屏二级水电站1号、2号引水隧洞穿越绿泥石片岩段出现局部变形>1 m，隧洞开挖期间出现大规模塌方、围岩持续大变形、临时支护结构破坏等现象[4]，严重影响隧洞施工安全,并造成费用的剧增。

为了对穿越绿泥石片岩的隧道大变形进行有效控制，近年来一些学者已经开展一系列研究。解亚东等[5]对穿越绿泥石片岩的何家寨隧道进行了施工方案的比选工作，提出采用环形开挖预留核心土穿越绿泥石片岩段可有效控制隧道发生大变形；Zhou等[6]分析了绿泥石片岩的物理特性以及对隧洞稳定性的影响，提出绿泥石片岩隧洞发生大变形的原因主要受控于隧洞埋深、地应力及岩体本身性质的影响，并且水对绿泥石片岩强度的影响十分显著；Zhang等[7]根据绿泥石片岩隧洞挤压变形段围岩变形特征，建立了多种变形指标围岩稳定控制方法，以围岩变形量和变形速率为主要指标及时调控，避免了深埋软岩挤压变形问题；陈建勋等[2-3,8-9]针对跨度大、断面扁平、地基承载力不足的连城山隧道分析其变形机理、变形规律，并提出采用“三台阶留核心土+大预留、多层、分次支护+大管径长锁脚锚管+深仰拱”的措施控制大变形；Yang等[10-12]介绍了锦屏二级引水电站1号隧洞绿泥石片岩段围岩大变形情况，采用二次扩挖、超前支护、新增拱架、增设锚杆及细水泥灌浆等综合措施成功解决绿泥石片岩段围岩稳定问题。数值模拟凭借其重复性好、可视化程度高等显著优势在隧道工程得到广泛应用，Huo等[13]对成昆超大断面的白云岩隧道采用有限元分析软件分别探究了围岩、初期支护及二衬对隧道的控制效果分析；霍润科等[14]对富水黄土隧道建立了渗流-应力耦合数值模型，分别分析了降水加固与注浆加固对地层变形的影响规律；邵珠山等[15]利用有限差分软件FLAC3D研究了小净距隧道的合理错距，并分析了不同开挖方案对隧道变形及应力的影响规律。

以上研究对绿泥石片岩隧道大变形机理的认识和相应控制措施的采用提供有益参考。但目前有关绿泥石片岩隧洞大变形规律的研究相关报道较少，国内现有研究主要围绕锦屏二级水电站[4,6,9-12]和连城山隧道[2-3,8]。但由于地质条件、断面设计，隧洞使用的支护参数、开挖工法等大有不同，隧洞在设计施工时多凭借经验结合现场实际确定施工方法和支护条件。因此，为进一步探索更适用于绿泥石片岩隧洞大变形控制措施，本文以滇中引水工程香炉山隧洞绿泥石片岩段为背景，探讨软岩隧洞更适用的本构模型，并对3种开挖方式引起隧洞变形进行对比，研究成果可为大埋深、高地应力软岩隧洞大变形控制积累经验。

2 岩体应变软化模型

2.1 Hoek-Brown屈服准则

Hoek-Brown(H-B)强度准则最早用于预测岩石破裂的经验公式。1980年由Hoke和Brown[16]基于Griffith的脆性断裂理论提出，通过输入岩石基本力学参数预测岩石的峰值强度，为矿山开采和支护体系提供所需岩石强度指标，具体表达式为

(1)

式中：σ1和σ3分别为岩体破坏时的最大和最小主应力；σc为完整岩体的无侧限抗压强度；m、s均为岩体H-B常数。m取值范围介于0.007～25之间，s取值范围介于0～1之间。

2002年Hoek等[17]引入扰动因子D(取值范围0～1)来描述施工扰动对岩石强度的影响，并对H-B强度准则进行了修正，其表达式为

σ1=σ3+σc(mbσ3/σc+s)a。

(2)

式中：mb为完整岩块mi的折算值；a为岩体H-B常数。

(3)

式中GSI为地质强度指标。

2.2 Hoek-Brown屈服准则应变软化模型

在岩石塑性应变软化模型中，屈服准则与塑性势能方程不仅由应力张量σ表达，还包括软化系数η，其弹塑性屈服准则[18]表示为

f(σθ,σγ,η)=0 。

(4)

式中：σθ为岩体切向应力；σγ为岩体的径向应力。

应变软化应力-应变简化曲线如图1所示。当η=0时，岩体处于理想弹性体；0<η<η*(η*为岩体弹性变形达到峰值后的软化系数)时，岩体处于应变软化阶段；η>η*时，岩体处于残余变形阶段。

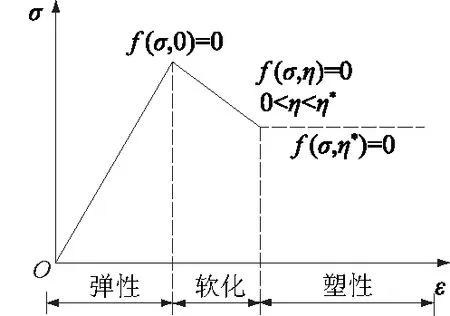
图1 应变软化曲线Fig.1 Strain softening curve

基于H-B屈服准则，岩体强度参数在峰后软化，假定强度是软化参数的双线性函数，其表达式为

(5)

式中：mp为峰值参数；mr为残余参数；m可代替H-B模型中的mb、s常数。

3 隧洞大变形特征

3.1 工程概况

滇中引水工程大理Ⅰ段施工3标地处滇西高原地区，位于云南省大理州鹤庆县松桂镇境内。工程主洞线路长约26.542 km，最大埋深1 450 m。隧洞钻爆段长度累计施工长度3.74 km，距鹤庆—洱源断裂带0.45 km，Ⅲ类围岩施工长度1 692 m，占45%；Ⅳ类围岩施工长度457 m，占12%；Ⅴ类围岩施工长度1 251 m，占34%；极端不良地质施工长度340 m，占9%。其中，研究区段DLⅠ7+478.6—459.6为绿帘石片岩与绿泥石片岩互层，隧洞岩层倾角近直立，拱顶发育缓倾角裂隙，如图2所示。隧洞断面设计如图3所示。支护形式包括超前支护与初期支护，具体支护参数设计见表1。

图2 隧洞掌子面节理Fig.2 Joints of the tunnel’s working face

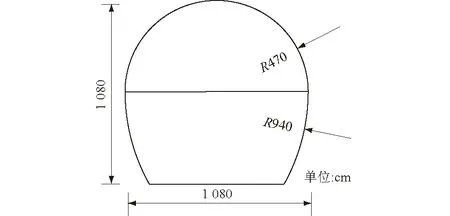
图3 隧洞断面设计Fig.3 Design of the tunnel’s cross-section

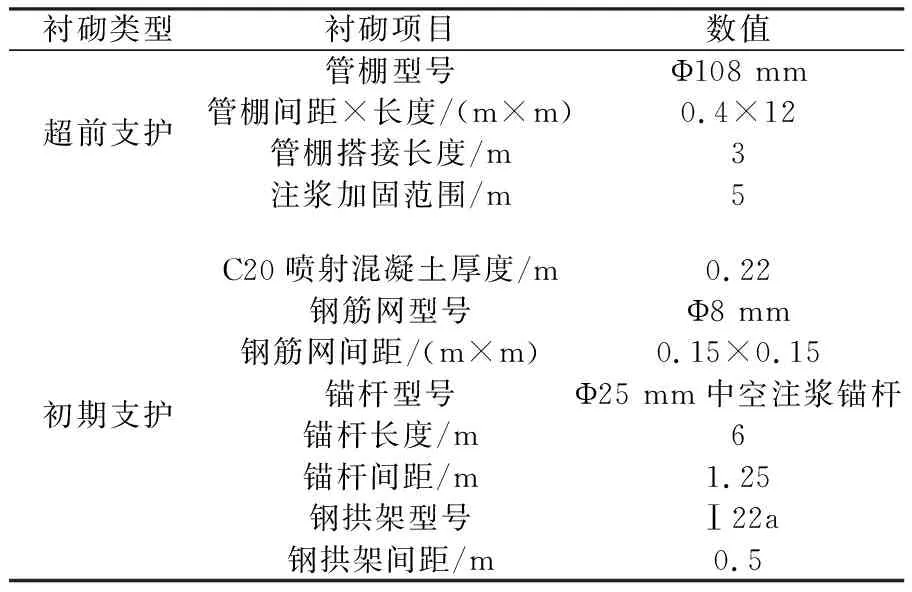
表1 隧道原始设计支护参数Table 1 Original design support parameters for the tunnel

3.2 围岩变形情况

该隧洞施工段变形破坏形式多样，如隧洞拱腰处钢拱架扭曲、局部拱顶坍塌、混凝土开裂、边墙挤压内鼓、底部隆起、拱顶下沉、钢筋网弯曲、钢拱架开裂等，具体变形如图4所示。

图4 隧洞施工段变形破坏形式Fig.4 Failure patterns of tunnel during construction

根据现场监测资料可知，围岩变形量大，且空间分布不均匀，水平收敛略大于拱顶沉降。隧洞DLⅠ 7+460断面拱顶沉降达到742 mm，拱腰处最大水平收敛位移达到768 mm。围岩初期变形速率达到40 mm/d，大变形段出现稳定收敛时间在20～30 d之间,表明香炉山隧洞具有变形量大、变形速率高、持续时间长的特点。

4 数值模拟分析

4.1 模型建立

本文依托工程实况建立地质模型，根据圣维南原理，为减少边界条件对模型的影响，模型左右侧及下侧取洞径3～5倍。模型顶部离隧洞拱顶40 m，数值模型由73 880个单元组成。模型尺寸为100 m(长)×24 m(宽)×90 m(高)，计算模型如图5所示。采用固定边界条件，模型底部施加法向约束，四周施加水平方向的约束。根据现场水压致裂法测得地应力资料，模型顶部施加初始地应力为12.5 MPa，侧压力系数λ为2。

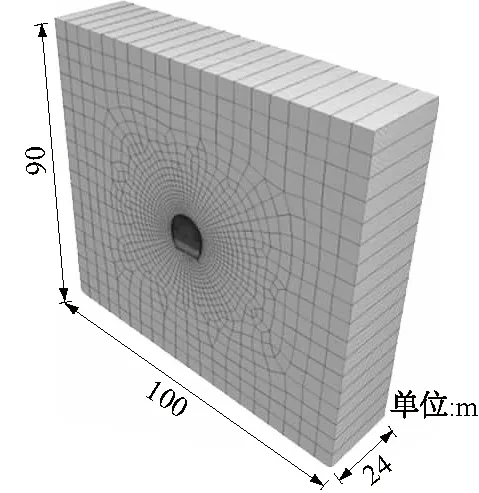
图5 模型整体示意Fig.5 Holistic view of the model tunnel

根据研究段实际施工情况模拟，该段尚未施作二次衬砌，模拟中不考虑二次衬砌作用。在数值模拟中，注浆加固区采用实体单元模拟；钢筋网+钢拱架+喷射混凝土的作用采用等效替代的原则来考虑，用shell单元进行模拟；锚杆采用cable单元模拟；超前管棚采用pile单元模拟。支护结构计算模型如图6所示。

三台阶预留核心土开挖过程：①初始地应力平衡；②上台阶开挖1.2 m，进行锚杆和初期支护施作；③上台阶开挖1.2 m后，上台阶和预留核心土同时开挖；④上台阶掘进3 m后，上台阶、预留核心土和中台阶同时开挖，并施作支护结构；⑤中台阶开挖3 m后，上台阶和预留核心土、中台阶和下台阶同时开挖，并施作衬砌。上台阶和预留核心土错开1.2 m，上、中、下台阶错开3 m，循环开挖进尺0.6 m。

4.2 参数选取

岩体和支护结构参数选取的真实可靠程度，直接影响数值模拟的准确性。考虑钢拱架和钢筋网的影响，本文通过抗弯刚度等效的原则提高喷射混凝土的弹性模量[19]。隧洞研究区段揭示出的地质岩性均为绿泥石片岩，节理发育、结构松散、岩石强度低。本次分析计算参数根据地勘资料和《公路隧道设计细则》(JTG/T D70—2010)进行修正，具体计算参数取值如表2所示。

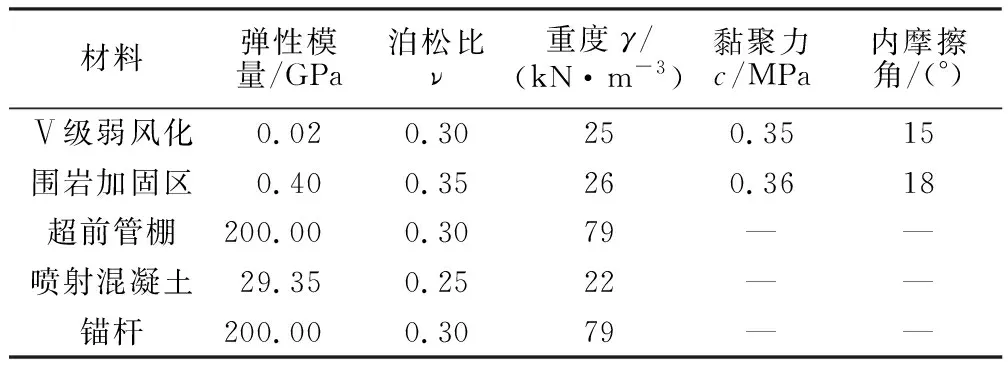
表2 模型材料计算参数Table 2 Calculated parameters of model materials

4.3 不同计算模型对比分析

为了避免边界条件的影响，选取模型中间断面进行分析。分别采用H-B应变软化模型和Mohr-Coulomb(M-C)理想弹塑性模型计算，得到隧洞拱顶沉降和应力随开挖循环步数与掌子面距监测断面距离的变化规律，如图7所示。

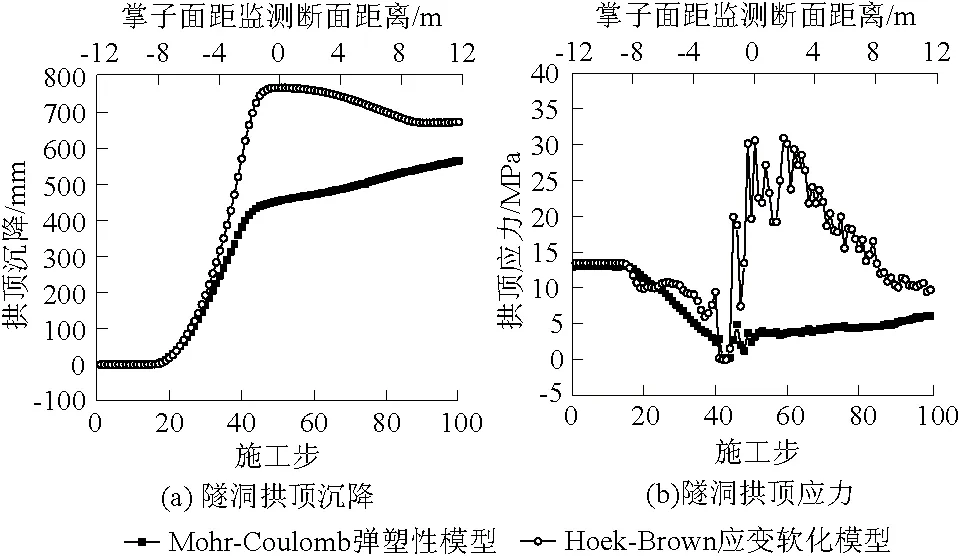
图7 隧洞拱顶沉降和拱顶应力随施工步变化曲线Fig.7 Variations of settlement and stress of tunnel’s arch top with construction steps

实际施工过程的变形最能反映隧洞的稳定状态，由图7(a)可知，采用应变软化本构模型隧洞拱顶最大沉降为766.7 mm，最终稳定时的沉降为672.3 mm，与实际变形相对误差为9.3%，说明本次数值模拟较为准确。然而理想弹塑性模型最大沉降量为565.2 mm，与实际监测数据对比相差了23.8%。由于H-B本构模型存在应变软化阶段，在模拟过程中导致隧洞拱顶沉降出现先增大后减小最后达到平衡状态；然而采用M-C本构模型并未考虑岩体应变软化过程，随着开挖步和掌子面距监测断面距离的增加，隧洞拱顶沉降缓慢增加。

由图7(b)可知，围岩初始应力为13.48 MPa，随着开挖步的进行，隧洞中间断面拱顶应力逐渐释放，沉降随之增加。施工步42—43时，应变软化模型和弹塑性模型应力值均达到最低。这是中间断面上台阶开挖导致监测点处围岩压力完全释放，降低为0 MPa。由于开挖完成后施作支护结构限制围岩持续变形，拱顶处围岩压力逐渐增加，直至围岩与支护结构达到新的平衡状态。围岩采用应变软化模型最终平衡状态应力为9.75 MPa，而使用弹塑性模型应力为6.09 MPa，并且随开挖步的进行,应力缓慢增加。在实际工程中，软岩隧洞具有明显的应变软化特性。因此，研究软岩数值模拟时，采用H-B应变软化本构模型更接近实际情况。

5 大变形控制效果分析

5.1 控制方案

在软岩隧洞施工过程中，选择合适的开挖工法对控制软岩隧洞大变形显得尤为重要。开挖工法的合理选择是控制大变形的前提，当开挖工法不适应隧洞所处地质环境条件时极有可能加剧大变形的发生，甚至导致重大灾害性事故发生。根据隧洞所处高应力绿泥石片岩的地质特点，结合隧洞埋深、长度、施工条件等特点，确定隧洞开挖工法的优选。由于隧洞处于Ⅲ—Ⅴ级软弱地层中，在高地应力软岩隧洞施工时，不适于全断面开挖；两台阶开挖法对工序要求高，若采用微台阶基本上是合为一个工作面进行同步掘进，与全断面开挖法基本相同，不适用于软岩隧洞开挖。故本次数值模拟采用分部开挖法，包括预留核心土台阶开挖法、单侧壁导坑开挖法和中隔壁开挖法进行变形控制比选(表3)。数值模拟中为减少循环开挖步和台阶长度对3种不同开挖工法的影响，三者循环开挖长度均取0.6 m，不同开挖部分间隔均取3 m。具体支护参数如表1所示。

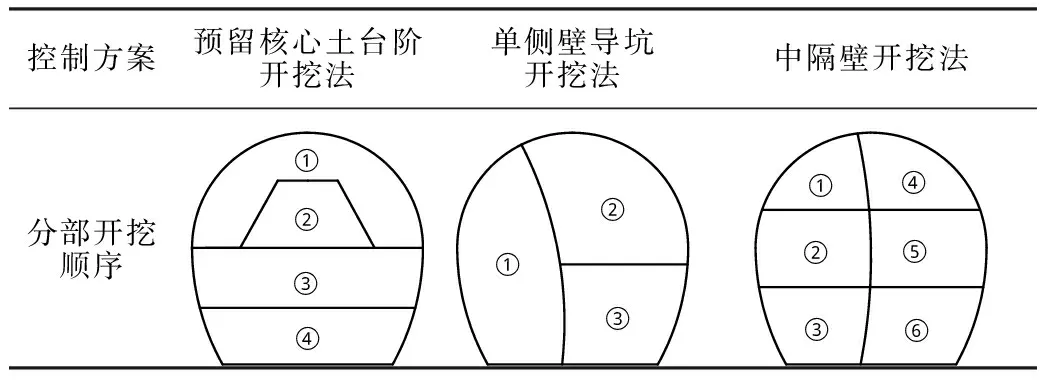
表3 控制方案Table 3 Control schemes

5.2 监测布置

数值模拟将监测断面设置在隧洞纵向12 m处，监测点布置都设置在隧洞拱肩、拱腰、拱墙处监测水平收敛，同时在拱顶设置一个监测点记录拱顶沉降量，监测布置如图8所示。

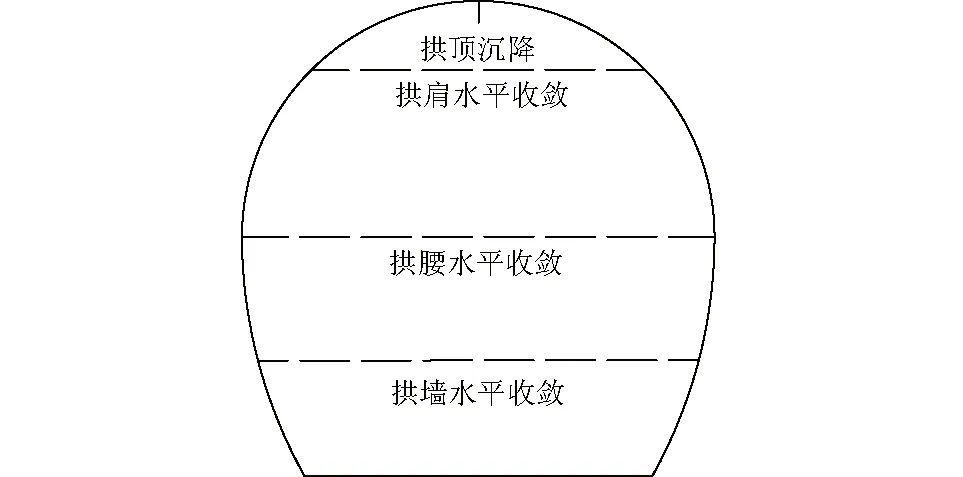
图8 监测布置Fig.8 Monitoring arrangement

5.3 结果分析

分别提取工况1—工况3数值模拟监测点位移结果，并绘制3种开挖工况下隧洞拱顶沉降和拱肩、拱腰以及拱墙水平收敛随施工步的变化曲线，如图9所示。

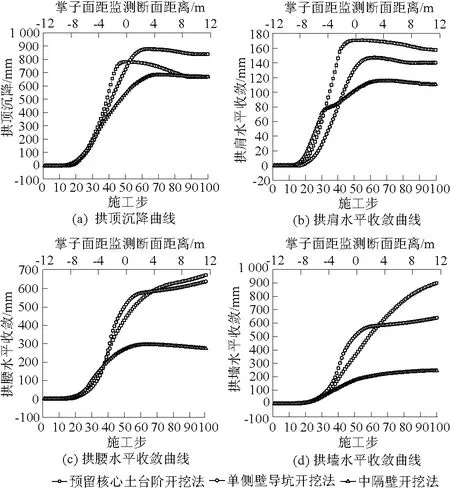
图9 不同开挖工况下隧洞拱顶沉降和拱肩、拱腰以及 拱墙水平收敛随施工步的变化曲线Fig.9 Variations of arch top settlement and horizontal convergence of arch shoulder, arch waist and arch wall under different excavation conditions

(1)由图9(a)可知，在施工步达到15步之前3种开挖工况对隧洞拱顶无扰动，随着距离监测断面距离的减少拱顶变形速率逐渐增大，隧洞施作衬砌后变形速率明显减少。并且随着开挖扰动的减少、衬砌作用使其沉降略有减少，当施工步为100时，拱顶变形最终基本稳定。数值模拟结果显示，工况2开挖导致拱顶沉降量最大，为878.1 mm，达到基本稳定时沉降量为839.2 mm；工况1拱顶沉降速率最大，其最大沉降766.7 mm，稳定时沉降672.3 mm；工况3开挖35步后沉降速率减缓，且相比其他两种开挖方法稳定时沉降量最小，当施工步为100时最终沉降量为669.2 mm。

对比3种开挖方法对拱顶沉降的影响，工况2完成侧壁导坑开挖时监测点处没有施作支护结构，导致拱顶处围岩应力松弛而发生大变形；工况1在上台阶开挖完成后可对拱顶及时施作初期支护，以及预留核心土可对掌子面施加一个反向推力，在支护力和反向推力作用下其沉降减少；工况3每开挖一部分施作中隔壁临时支护，避免出现由于拱顶围岩应力松弛而增大沉降的现象。

(2)由图9(b)可知，工况1和工况2对拱肩水平收敛的影响曲线变化趋势相同，然而工况3对拱肩收敛曲线的影响分两个阶段。第一阶段是开挖左上部分导致拱肩变形速率迅速增加，第二阶段是及时施作初期支护及临时中隔壁引起变形速率降低，最后趋于基本稳定。数值模拟结果显示，工况1引起拱肩最大水平收敛170.9 mm，基本稳定时收敛157.6 mm；工况2引起拱肩最大水平收敛147.1 mm，基本稳定时收敛140.2 mm；工况3引起拱肩最大水平收敛115.3 mm，基本稳定时收敛110.5 mm。

对比3种开挖方法对拱肩水平收敛的影响，工况1上台阶开挖后施作初期支护限制围岩产生水平位移，且左右拱肩处同时挖除导致变形速率较大。但工况2在左侧导坑开挖后拱肩处施作临时中隔壁以及右侧未开挖的岩体限制拱肩围岩的水平位移，因此，工况2开挖引起拱肩水平收敛较小于工况1。工况3开挖次数较多，拱肩处围岩更早受到开挖扰动的影响，但在初期支护和临时中隔壁的支护下所限制的变形量最大。

(3)由图9(c)可知，工况1和工况2随施工步的进行,其拱腰水平收敛持续增加，工况3在开挖任意一侧上中下台阶时分别施作临时中隔壁可限制拱腰水平收敛，因此拱腰变形值最小。数值模拟结果显示，在施工步为100时，工况1拱腰水平收敛674.3 mm；工况2收敛638.9 mm；而工况3在施作支护结构之前最大收敛295.1 mm，随支护结构的限制作用其最终收敛为273.5 mm。

对比3种开挖方法对拱腰水平收敛的影响，工况1和工况2在受到开挖扰动作用其变形速率相近。当施工步进行到监测断面时，工况2挖除左侧导坑导致其变形速率增加。工况1和工况2除初期支护作用力外无其他措施限制拱腰处围岩变形，导致随施工步进行其收敛持续增加。工况3在初期支护和中隔壁作用下使得拱腰变形大幅下降。

(4)由图9(d)可知，工况1随施工步的进行其拱墙水平收敛逐渐增大；工况2拱墙水平收敛曲线与其拱腰收敛曲线相近；而工况3拱墙水平收敛最小。数值模拟结果显示，当施工步为100时，工况1拱墙水平收敛最大，为898.7 mm；工况2最终收敛638.9 mm；工况3达到基本稳定收敛，为244.8 mm。

对比3种开挖方法对拱墙水平收敛的影响，工况1开挖到监测断面下台阶时拱墙变形持续增大，说明设计的初期支护参数无法限制拱墙发生大变形。工况2开挖左侧导坑导致拱墙变形速率急剧增加，待初期支护和临时中隔墙施作后其变形速率明显减少，但仍未完全限制拱墙持续变形。工况3分部开挖后临时中隔壁和初期支护封闭成环较好的限制拱墙变形，其变形相比于工况1和工况2更小。

提取3种开挖工况的数值模拟数据结果进行对比分析，结果如表4所示。

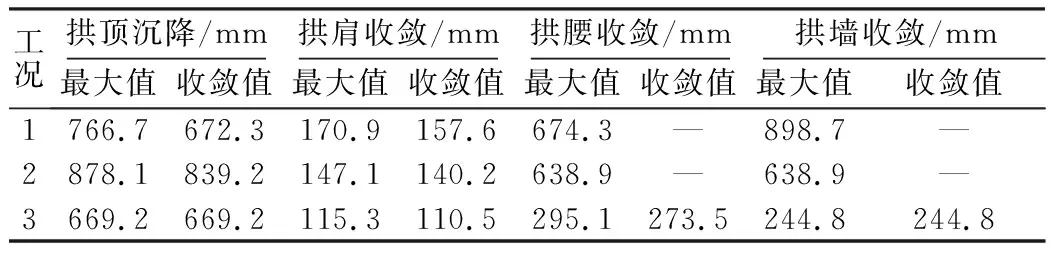
表4 不同工况的数值模拟结果对比分析Table 4 Comparative analysis of numerical simulated results under different excavation conditions

由表4可知：隧洞断面明显出现不均匀大变形，拱顶位置在超前支护及初期支护作用下可限制拱顶持续发生大变形，但其变形值仍然过大，应在原设计基础上增加支护参数。工况1和工况2在施工步内拱腰及拱墙变形不能趋于收敛，其原因是水平地应力较大，初期支护不能完全限制其变形。

工况2相比于工况1而言，拱肩收敛减少了11%，拱腰收敛减少5%，拱墙收敛减少了28%；然而工况2开挖对拱顶沉降不能起到良好的限制作用，相对于工况1和工况3拱顶沉降增加20%左右，不适于软岩隧洞的开挖。

工况3的开挖工法对比工况1和工况2增加了横向临时中隔壁，使隧洞整个断面的变形值都大幅降低。对于拱腰和拱墙收敛相对于实际工程中采用的预留核心土台阶开挖法分别降低了56%、72%。并比较3种开挖方法监测断面塑性区的分布，如图10所示。根据大变形控制效果及塑性区分布来看，采用工况3进行软岩隧洞开挖更有利于施工安全。

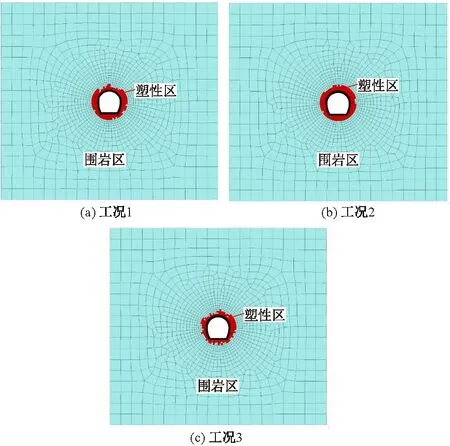
图10 不同工况下隧道开挖塑性区分布Fig.10 Plastic zone distribution under different excavation conditions

6 结 论

依托滇中引水工程香炉山隧洞，分析了隧洞大变形情况，确定了深埋绿泥石片岩隧洞在数值模拟中更为适用的本构模型，并采取不同开挖方式探究对大变形的控制效果，得到如下主要结论:

(1)香炉山隧洞埋深大、应力高，绿泥石片岩工程力学性质差，岩体破碎、节理发育、结构松散，自稳能力差，造成施工过程中围岩发生大变形甚至造成隧洞支护结构严重破坏。

(2)隧洞变形量大，实际拱顶累计沉降达到742 mm，由于水平地应力较大，拱腰最大水平收敛达到768 mm。隧洞拱腰和拱墙为大变形灾害主要部位，向内挤出变形现象严重，拱顶处向下沉降。

(3)分别采用应变软化本构模型和理想弹塑性模型对软岩隧洞进行模拟，模拟结果显示，应变软化本构模拟软岩隧洞其拱顶沉降与实际值误差为9.3%，验证了该本构模型适用于软岩隧洞的模拟。

(4)从隧洞大变形控制效果来看，工况3对隧洞拱顶沉降和拱肩收敛的控制效果相对于工况1和工况2减小了20%左右，但在横向临时中隔壁的作用下隧洞拱腰和拱墙的水平收敛减少了60%左右。因此，采用中隔壁开挖法可以有效解决绿泥石片岩隧洞关键部位大变形问题。