基于视觉系统的倾角仪自动化校准装置

陈浩 邹文哲 刘闯 / .上海市计量测试技术研究院； .上海大学机械工程与自动化学院

0 引言

倾角仪作为测量角度的常用设备，是一种用于测量一个平面（或圆柱面）相对于水平面的倾斜角及平面（或圆柱面）之间夹角的仪器，包括采用电子倾角传感器的电子数显倾角仪和机械倾角测量机构的光学倾斜仪[1-2]。市场上的数显角度测量设备外形、尺寸多种多样。目前，校准数显倾角仪常用的方法主要采用光学分度头手工测量，或正弦规搭配量块进行角度模拟来间接测量这两种方法。其中光学分度头因靠人工手动控制，操作较为繁琐，正弦规搭配量块受量块尺寸组合影响，只能对特定角度校准有较高的准确度[3-4]。本文设计了一套基于视觉系统的倾角仪自动化校准装置，来弥补传统测量方法的不足之处。

1 倾角仪自动校准装置

为解决现存正弦规加量块的组合校准方法以及光学分度头直接测量方法所存在的人为误差，以现有市场上的数显分度头为基础进行自动化设计。现有设备的传动装置体积较大，整体相对笨重且需要手动操作。

本项目改良了传统的传动装置，选用由电机驱动的传动装置控制圆光栅编码器的定位。鉴于倾角仪自动化校准装置分辨力高，一般的电机无法达到如此高精度的转动定位，所以仅以电机作为驱动，对仪器内部的传动机构（丝杆螺母、齿轮等）进行重新设计和定制，达到所需传动比并满足角度定位需求。此过程将减小装置内部结构的体积，使整套装置更加紧凑，实现装置的轻量化。重新设计后装置体积可减小约1/2[5]，整套装置传动如图1所示。

图1 传动示意图

倾角仪自动化校准装置选用步进电机进行驱动，减速齿轮机构将电机的转速降低，经齿轮传动后的转动量经传动装置传递到圆光栅编码器，实现角度定位。将编码器、夹具和倾角仪固定至同一根传动轴，从而消除编码器与倾角仪转动过程中的相对误差。选用绝对式编码器，其输出通常为二进制码。从代码数大小的变化可以判别正反方向和位移所处的位置，绝对零位代码还可以用于停电位置记忆。此类编码器的特点是可以直接读出角度坐标的绝对值，没有累积误差，电源切断后位置信息不会丢失[6-7]。

校准装置在转动过程中，其基准面和夹具形成了一个变化的力矩。为了平衡该力矩，选用的步进电机需要具有合适的阻尼，避免整个装置在转动过程中出现突然的加速度，造成被测样品的抖动或示值漂移。

2 基于CCD摄像头的视觉系统

本次自动化设计将使用自动读取示值装置代替人工，达到提高校准效率、降低劳动强度的目的，校准过程如图2所示。

图2 校准过程

自动读取示值通过CCD摄像头实现。实验室常见的送检样品，其分辨力为0.01° ～0.1°。在实际操作中，测量人员将样品固定在基准面上，调整摄像头完成对焦，待计算机端软件上能正确显示示值后，进行清零操作并开始校准。整个校准过程中，摄像头随被测样品一同转动，两者之间没有相对位移和偏差，因此，不需要操作者进行多次对焦和调整。

在控制系统中，通过计算机程序对转动参数进行设置，由运动控制卡对步进电机旋转角度和转动速度进行控制，同时圆光栅编码器的角度信号通过运动控制卡传输至计算机。CCD摄像头采集被测样品的示值图像并传输至计算机中，通过数字识别得到其示值数据并储存。

3 试验数据采集及不确定度分析

因分辨力为0.1°的数显倾角仪重复性数据几乎无变化，本装置将对分辨力0.01°数显倾角仪进行数据采集和不确定度分析。

3.1 测量过程

将分辨力0.01°数显倾角仪装夹在倾角仪校准装置上。对各校准角度进行读取，被测仪器的示值误差是以该点示值与倾角仪校准装置标准角度值之差。

3.2 测量模型

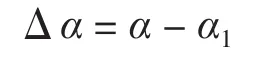
式中：Δα——数显倾角仪的示值误差；

α——数显倾角仪的示值；

α1——倾角仪校准装置的标准角度值

3.3 灵敏系数

依据测量模型，则灵敏系数为

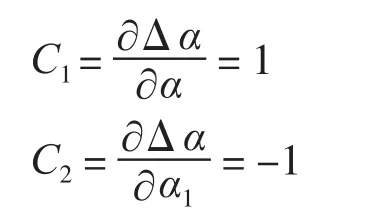
3.4 输入量的标准不确定度评定

输入量的标准不确定度主要来源为被测样品重复性引入的不确定度和数显角度仪校准装置引入的不确定度。

3.4.1 数显倾角仪重复性引入的标准不确定度u(α1)的评定

u(α1)采用A类方法进行评定。

对30°角度点在重复性条件下测量10次，得到数据见表1。

表1 数显倾角仪30°实测数据

由贝塞尔公式：

数显倾角仪分度值量化误差引入的标准不确定度为

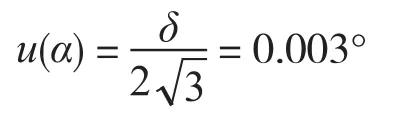
式中：δ——被测数显倾角仪的分度值

因分度值量化误差引入的不确定度大于重复性误差引入的不确定度，因此，对于分度值为0.01°的数显倾角仪 ：u(α1) = 0.003°[8]。

3.4.2 标准器引入的标准不确定度u(α2)的评定

标准器引入的不确定度u(α2)主要来源于倾角仪校准装置的示值误差和分辨力引入的标准不确定度

3.4.2.1 倾角仪校准装置的示值误差引入的标准不确定度u(α21)

倾角仪校准装置的示值误差为±4''，取其半宽区间4''，转化为角度0.001 1°。设在区间内服从均匀分布，倾角仪校准装置的示值误差引入的标准不确定度，所以

3.4.2.2 倾角仪校准装置的分辨力引入的标准不确定度u(α22)

倾角仪校准装置分辨力为1''，取其半宽区间0.000 14°。设在区间内服从均匀分布，则倾角仪校准装置分辨力引入的标准不确定度：

由以上两项得出由标准器倾角仪校准装置引入的标准不确定度：

3.4.3 专用夹具安装误差估算的不确定度分量u(α3)

数显倾角仪专用夹具在安装时，由操作误差引起测角误差，最大变化为0.002°，区间半宽度为0.001°。设其在区间内为矩形分布，因此，安装误差引入的不确定度[9-10]：

3.4.4 倾角仪安装误差

数显倾角仪由专用夹具固定而引起的测角误差u(α4)，最大变化为 0.003°，区间半宽度为 0.001 5°。设其在区间内为矩形分布，因此，安装误差引入的不确定度：

3.5 合成标准不确定度uc的评定

输入量均彼此独立不相关，所以得

3.6 扩展不确定度的评定

数显倾角仪的示值误差扩展不确定度评定：

因为分度值误差主要为均匀分布，取k值为2，数显倾角仪分度值0.01°时，

同理可得数显倾角仪分度值0.05°时，

同理可得数显倾角仪分度值0.1°时，

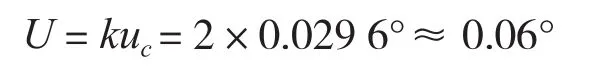
4 数显倾角仪不同方法示值误差测量结果比对

本次比对采用了三种不同设备对同一分辨力为0.01°的数显倾角仪进行比对测量。结果如表2所示。

表2 比对数据汇总

已知倾角仪校准装置对0.01°数显倾角仪示值误差测量结果不确定度为U1= 0.007°（k= 2）。根据JJF 1117-2010比对法要求，得出：

5 结语

本文设计了一种新的数显倾角仪校准装置来实现对倾角仪的示值误差校准。该校准方法主要是解决现存校准方法所存在的人为误差，同时提供一种操作简单、使用便利的自动化校准方法，减少了倾角仪校准误差，缩减了送检时间和送检成本。