基于蚁群算法的消防安全疏散路线仿真研究

唐 黎

（黄浦区消防救援支队，上海 200011）

随着城市规模不断扩大，城市内大型建筑越来越多。这些大型建筑用于商业或者用于住宅，都发挥了非常重要的作用。大型建筑面临的最大的安全隐患是突发火灾等恶性事故时的救援[1]。因此，如何为这些大型建筑设计合理的消防安全疏散路线，不仅关乎大型建筑总体设计的合理性问题，也关乎其投入使用后是否会具有足够的安全保障[2]。合理的消防安全疏散路线，可以快速疏散密集的人群，最大限度地挽回生命和财产损失。消防安全疏散路线的设计，可以采取经验法、常规布局分析法和智能模型分析法[3]。其中，智能模型分析法不仅可以得到更快速的设计结果，其合理性也更高。因此，该文选择蚁群算法进行大型建筑的疏散路线设计，以期更好地提升其消防安全水平。

1 基于蚁群算法的路径搜索

大型建筑一旦发生火灾会增加危险性，造成重大的生命和财产损失。出现该情况的原因有以下2点：1）大型建筑内部容纳的人员数量密集，一旦发生火灾会在短时间内形成拥堵，无法到达指定的安全出口逃生，从而导致大量的人员伤亡。2）大型建筑内部的建筑结构复杂，障碍物很多，如果叠加疏散路线不合理的情况，就会导致火灾发生后，人们无法及时发现逃生出口，从而导致大量伤亡。因此，大型建筑的消防安全问题的核心是疏散路线的优化。

大型建筑消防安全的路线规划的工作如下：首先，须对大型建筑内的障碍、可行道路灯信息进行建模描述，进而抽象成1张二维的平面地图。有了这张二维地图，就可以通过相应的方法对疏散路线进行选择和设计。基于常规的路线选择方法包括栅格法和几拓扑图法等。这些方法也可以作为进一步使用蚁群算法进行智能寻优的前提。首先根据栅格法对大型建筑物的内部环境进行建模。假设大型加筑物内部环境可以描述为n×n个栅格，其内的坐标关系如公式（1）所示。

式中：x为大型建筑二维地图中的横坐标；y为大型建筑二维地图中的纵坐标；W为大型建筑二维地图全部栅格的宽度；mod（）为取模处理函数。

蚁群算法是智能优化算法领域中开发比较成熟的一种方法，通过学习蚂蚁群体智能构建出的一种启发模式算法。蚂蚁个体经过1条路径后，会在关键点位留下信息素。如果多个蚂蚁个体都认为某一点为关键点，那么这个关键点上的信息素浓度就会越来越多。将这些关键点连接起来，就成了一条最合理的路径。

蚂蚁群体智能抽象出来的蚁群算法，假定在t时刻，第k只蚂蚁个体从标号为i的位置向标号为j的位置进行移动，这种情况发生的概率如公式（2）所示。

式中：ρij（t）为蚂蚁从i位置运动到j位置的信息素浓度；ηij（t）为蚂蚁从i位置运动到j位置启发权重为i与j的距离。

每个蚂蚁个体在行进过程中都会留下信息素。这样，一个位置经过的蚂蚁越多，这个信息素浓度就会越高。基于此，蚁群算法中信息素的更新处理如公式（3）~公式（5）所示。

式中：Q为信息素强度；Lk为蚂蚁一共k经过同一路径的长度。

蚁群算法通过多个蚂蚁个体的设置，有利于优化算法并行执行，因此优化效率高。但是，蚁群算法的搜索机制设定不合理时，算法的收敛速度会变慢。同时，复杂的优化问题容易造成蚂蚁个体落入局部最优陷阱，无法找到全局最优方案。为此，该文从搜索策略、信息素更新策略、路径优化策略3个方面进行改进，得到一种性能更好的蚁群算法。

2 蚁群算法的改进处理

2.1 搜索策略的改进

蚁群算法在结构化的地图中进行寻优时，搜索策略是比较单一的，即以1个单位的固定补偿进行搜索。对该文的栅格化地图图像，其搜索步长就是1个栅格长度。这样的处理不仅缺乏灵活性，也会降低搜索过程的效率，导致蚁群算法的收敛速度变慢。该文中对搜索策略的改进处理如下：如果蚂蚁个体所代表的波形轨迹点呈现同向变化，则搜索步长可以增加，即不固定设置为1个单位。多步长搜索策略如图1和图2所示。

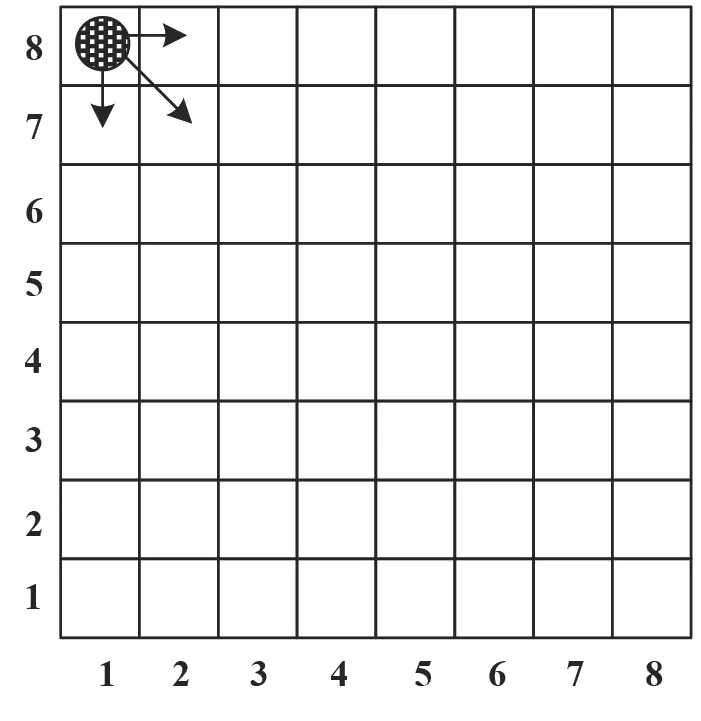
图1 单步长搜索策略

图2 多步长搜索策略

图1代表了传统蚁群算法的一步搜索步长设定，图2代表了该文改进后的搜索步长设定，这里是设置了一步搜索3个步长单位。从图1和图2可以看出，通过该文的改进处理，蚂蚁个体的搜索范围加大、搜索视野开阔、搜索效率提升。

2.2 信息素更新策略的改进

如果一个蚂蚁个体已经找到了最优路径，但其余蚂蚁个体并未经过此路径，那么这条路径上的点留下的整体信息素浓度就会很低。这条本应该正确的最优路径，也会因为信息素浓度不足而遭到淘汰。这不仅会导致算法无法找到最优路径，甚至可能陷入局部极小问题。为此，该文对一个蚂蚁个体可以确定的最优路径上的各点，给予额外的信息素浓度补偿机制，具体的处理如公式（6）和公式（7）所示。

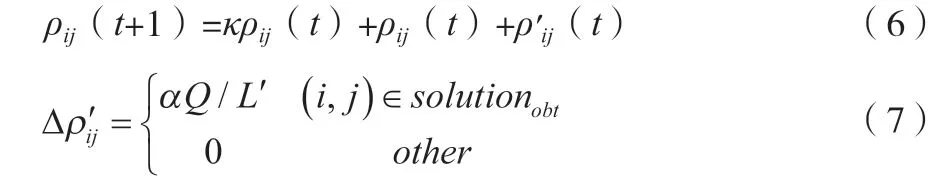
式中：Δρ'ij表示了额外的信息素浓度补偿；L'表示一个蚂蚁个体找到的最优路径长度；solutionobt表示整个算法找到的候选最优解的集合。

当蚁群算法陷入局部极小时，会反复在局部路径上进行行走，导致局部路径上信息素浓度不断升高，而蚂蚁个体却无法逃离此路径。为此，该文对此时的处理配置了信息素浓度递减机制。如果一个点位上的信息素浓度不断增加，这个点又确定不是最优路径上的点，那么这个点位上再有蚂蚁个体经过，信息素浓度不是增加而是减少。信息素浓度递减处理如公式（8）所示。

式中：λ为惩罚系数，λ的大小与蚂蚁个体经过某一点位的总次数成正比。

2.3 路径优化策略的改进

疏散路径中有时会出现路线上有尖峰的情况。考虑到该问题，在蚁群算法的路径优化过程中，对具有尖峰形态的路径段进行平滑处理。如果路径在某一局部的转弯处形成的角度极为尖锐，就可以认定为尖峰出现。对尖峰两侧的线段，在其夹角区域内选取一个中点，中点坐标的计算如公式（9）和公式（10）所示。

式中：（xold1，yold1）、（xold2，yold2）分别为尖峰附近两侧线段上的点，（xnew，ynew）代表了得到的新的中点。

将这3个点进行连线，则可以平滑掉原有的尖峰。

2.4 算法流程设计

为了优化基于蚁群算法的大型建筑消防安全疏散路线，设计的算法流程包括以下7个环节：第一个环节，将大型建筑的内部环境抽象为二维的平面地图，并且进行栅格化处理，同时对算法的初始状态进行配置，并且设定不能经过的障碍信息。第二个环节，将M只蚂蚁个体随机安放到大型建筑抽象出来的二维平面地图中，开始进行疏散路线优化。第三个环节，根据该文提出的多步长选择策略，以更高的效率搜索疏散路线，并不断更新可行节点和备选路线。第四个环节，如果某一个蚂蚁个体陷入了局部极小状态，按照该文的信息素递减机制成功退出该节点，避免算法进入死循环。第五个环节，根据该文提出的信息素额外增加机制，更合理地更新每个节点的信息素浓度。第六个环节，根据迭代误差是否达到极小，判断整个算法是否结束，如仍未结束继续前面的各个环节。第七个环节，当整个算法满足结束条件时，跳出迭代过程，并将此时的结果输出作为大型建筑消防安全的最佳疏散路线。

3 试验结果与分析

为了验证该文建立的蚁群算法对大型建筑消防安全疏散路线优化的有效性，进一步通过试验加以验证。在该试验过程中，大型建筑的真实环境被抽象成16×16栅格大小的二维地图。在该场景中，正常设定的入口位置在栅格标号为（1，16）的位置，正常设定的出口位置在栅格标号为（14，1）的位置。

消防安全疏散路线的验证试验中，蚁群算法的初始条件设定如下：参与搜索路径的蚂蚁总个数为20个，迭代过程规定不超过300次，启发系数α=1.0，启发系数β=5.0，信息素挥发因子λ=0.5，信息素浓度系数Q=100，路径不合理对应的惩罚系数κ=0.3。

在上述试验条件下，采用该文设定的蚁群算法进行大型建筑的消防安全疏散路线优化，得到的结果如图3所示。

图3中，上方圆点表示大型建筑正常的入口位置，下方圆点表示大型建筑正常的出口位置，白色网格表示人群可以正常通行的区域，黑砂网格表示障碍或者无法通行的区域。图中的粗实线是经过该文提出的算法规划出的人群可以较为便利、更宽敞的通行路径。根据改进蚁群算法得到的这个通行路径网络，算法设计了除进口以外的5个最佳逃生出口，以备发生火灾时进行人群疏散。这五个逃生出口全部用长方形黑色粗实线框标记，并根据位置不同配置了A、B、C、D、E5个标号。从图中的配置情况可以看出，5个逃生出口都在相对宽敞、人群容易疏散的位置，说明该文提出的改进蚁群算法对大型建筑消防安全人群疏散路径设计的合理性和有效性。为了进一步考察该文算法的性能，将该文算法和改进前的传统蚁群算法进行对比，结果见表1。

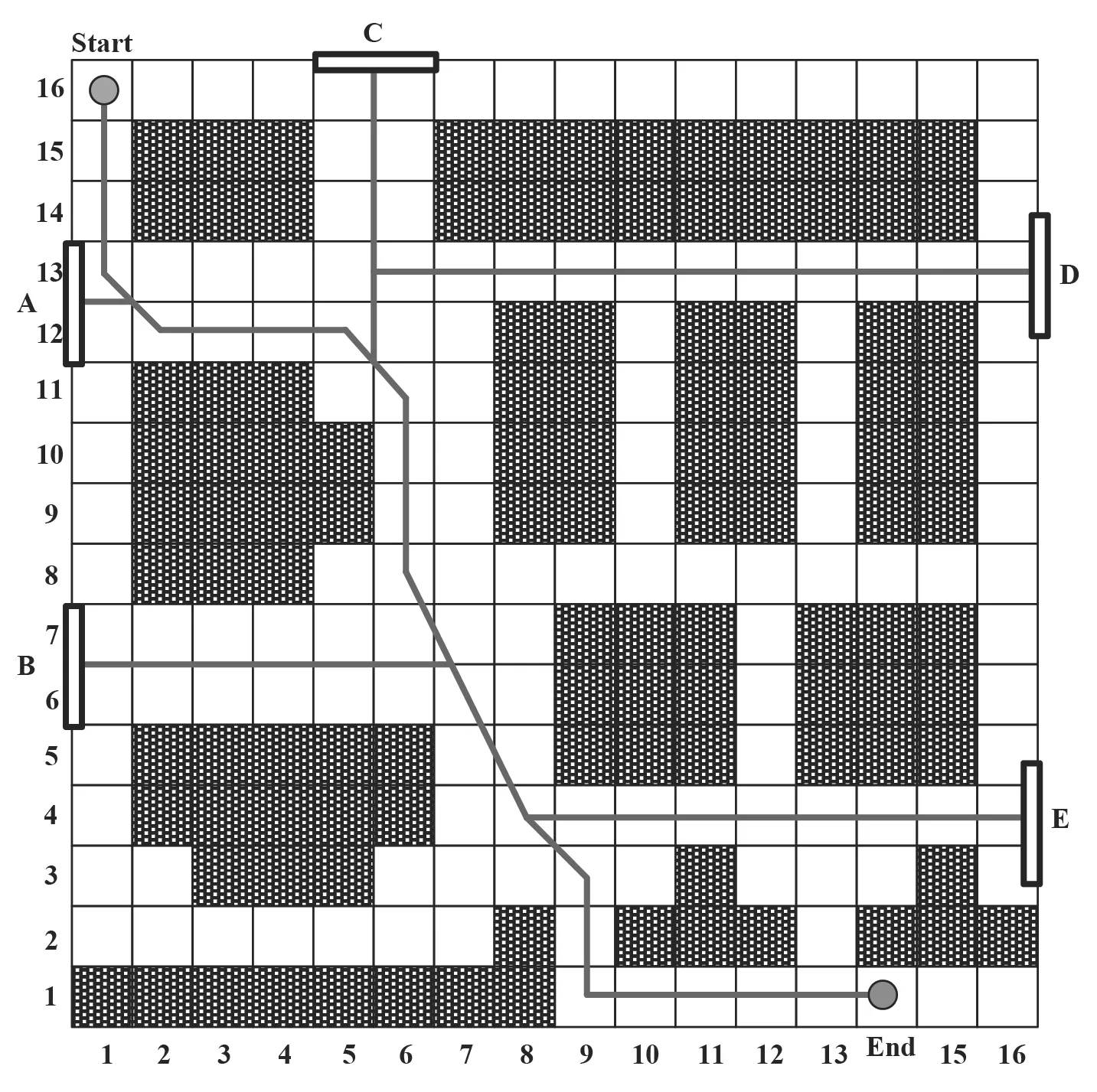
图3 大型建筑消防安全疏散路线的蚁群算法优化结果

从表1中的数据可以看出，与传统蚁群算法相比，该文改进处理后的算法对大型建筑消防安全疏散路线的搜索结果，在各项关键参数中全部体现了明显的优势，进一步提升大型建筑消防安全的可靠性。

表1 该文算法和传统蚁群算法的对比

4 结论

随着城市的快速发展，大型建筑不断出现，大型建筑的消防安全工作也成为消防工作的重要内容。为了给大型建筑设计更好的疏散路线，该文在蚁群算法的基础上改进，形成多步搜索策略、增加了信息素更新机制、设计了路线优化流程。针对大型建筑的二维地图疏散路线试验研究结果表明，该文方法可以得到更丰富、更合理的疏散路线和逃生出口。该文方法与传统蚁群算法相比，各项参数都有更明显的优势，更适用于大型建筑的消防安全工作。