PMMA墙体单侧受火状态下的温度特征分析

何 豪 汪圣华

（1.天津大学电气自动化与信息工程学院，天津 300072；2.中国计量大学质量与安全工程学院，浙江 杭州 310018；3.浙江省应急管理科学研究院，浙江 杭州 310020）

0 引言

PMMA是一种透明的有机高分子材料，其化学名为聚甲基丙烯酸甲酯，分子式为（C5O2H8）n。作为一种常见的聚合物材料，PMMA具有良好的力学性能和耐候性，因其透光性好，在仪器仪表、汽车车灯、光学镜片以及建筑透明管道等方面具有广阔的应用前景。

作为一种典型的有机高分子材料，PMMA同样存在易燃、发烟量大且毒性强等问题，其火灾安全性也受到人们的普遍关注。如罗圣峰等人建立固相传热和熔融相变模型，通过数值模拟方法考察了PMMA板材逆流火蔓延过程[1]。王康等人采用锥形量热仪研究了不同热辐射通量对PMMA燃烧特性的影响[2]。周小二等人以氧指数和垂直燃烧方法对PMMA材料添加三种磷系阻燃剂的燃烧及物理性能进行了表征，比较了不同阻燃剂对复合材料阻燃效率、增塑作用、拉伸强度以及光学性能的影响[3]。上述研究为PMMA的广泛应用提供了一定参考依据。

实际火灾场景中，PMMA墙体可能会受到火焰热辐射作用，带来热解及燃烧，进而对其结构造成破坏。PMMA的熔融、热解甚至燃烧都与其温度特征密切相关。因此，研究其在火场尤其是单侧受火状态下的温度特征，对评估其火灾危险性具有明确的现实意义。

1 模型建立及物性参数

采用传热模型考察PMMA墙体的温度变化，建立如图1所示的火灾模拟场景。其中，一定厚度的PMMA置于水体和火场之间，左侧为质量无限大的水体，由于水的比热及传热速率都较大，而亚克力板的热传导速率较小，右侧火焰透过板材传导的热量十分有限，故在模拟过程可假定水体温度恒定。右侧受到来自火焰的辐射热流，假定该辐射热流密度不随PMMA厚度及表面温度的变化而变化。

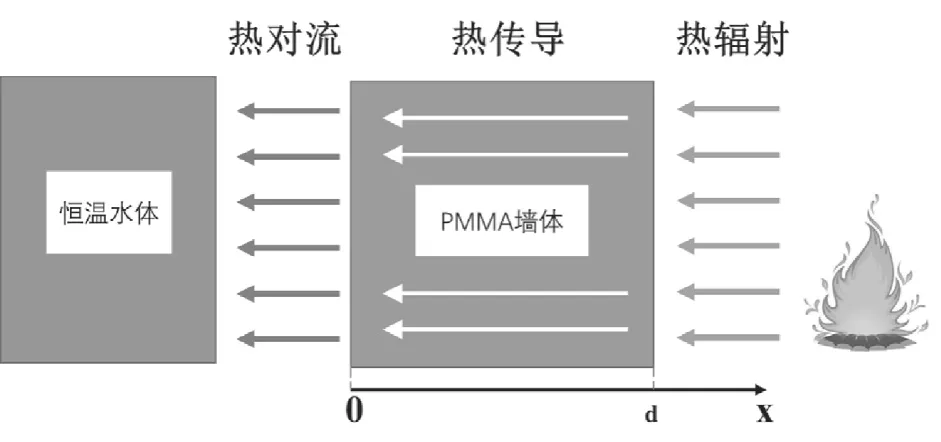
图1 传热模型示意

由于火焰对PMMA的热辐射作用在相当大的表面上，且热流密度均匀分布，故在板材内部，仅有垂直于板材表面方向的热传导，而不考虑在平行于板材表面方向上的热传导，即采用一维模型来近似。因此该传热问题看作是一维非稳态热传导问题，基本的传热方程如公式（1）所示。

式中：T为温度；t为受热时间；d为PMMA墙体厚度；x为板材内部节点距离板左边界外表面的距离（0＜x＜d）；α为热扩散系数。

初始条件，即0时刻，左边界温度T（x=0）=Tw，右边界温度T（x=d）=T∞，内部温度成线性分布。

式中：Tw为水体温度；qw为表面吸收的辐射热流密度；T∞为环境温度；k为热导率；h为对流换热系数。上述方程中，为温度项在x方向的二阶梯度为温度项在x方向的一阶梯度为温度项随时间变化的一阶梯度。

传热模拟重点关注PMMA在一定热流密度下的厚度变化。如果某部分温度超过热解温度，由于热解作用造成该部分的质量损失，后续不适合继续参与传热计算，因此在进行传热模拟时，当某部分温度超过稳定热解温度时，即认为该部分材料不存在，后续计算将舍弃该部分，即在模拟过程中材料厚度不断减小。

根据龚俊辉等人的研究结果，在热流密度为20 kW/m2、40 kW/m2、60 kW/m2时，照射到PMMA表面被吸收用于加热和热解的热量占总入射热流密度的比例为60%左右[4]，其他均已对流和辐射的形式通过表面散失到环境中。由热辐射理论可知，如果表面温度升高热辐射作用就会增强，也就是说被吸收用于加热和热解的热量占比将有所下降。

上述传热模型涉及的物性参数见表1。例如密度、热导率、软化温度以及热导率等，并且将PMMA的热扩散系数与其他常见物质进行比较，见表2。

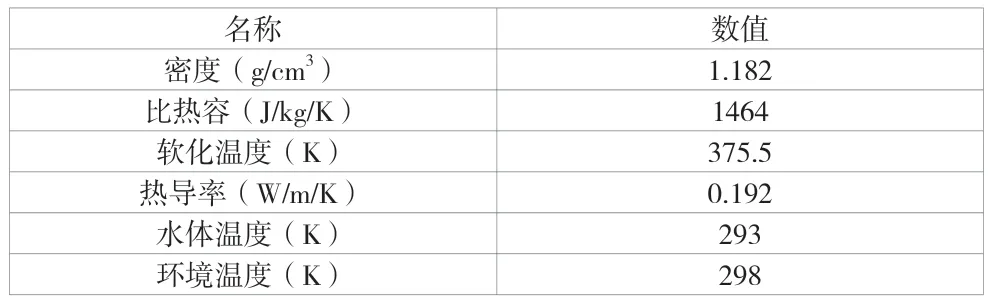
表1 基本物性参数

表2 常见物质的热扩散系数

2 代数方程离散化

通常情况下，使用代数方法求解传热模型得到其解析解存在很多困难，可采用数值方法进行求解。数值解法的基本思想是用传热问题所涉及的空间和时间区域内有限个离散点（又称为节点）的温度近似值来代替物体内实际连续的温度分布，将连续温度分布函数的求解问题转化为各节点温度值的求解问题，将传热微分方程的求解问题转化为节点温度代数方程的求解问题。因此，求解区域的离散化、节点温度代数方程组的建立与求解是数值解法的主要内容。

利用控制容积法对求解区域——即厚度为d的PMMA进行网格划分。采用均匀网格，取总的节点数量为N+1，其中边界节点（编号0、N）为半节点，内部节点用数字1-N-1来表示，第i节点即代表第i个子区域，该节点的温度就是该节点区域的温度。

采用全隐式格式进行偏微分方程的离散。那么，对内部节点（i=1-N-1），公式（1）的传热方程可转化如公式（4）所示。

式中：Δx为空间步长，且为时间步长。以上N+1个等式共同构成了一个N+1元代数方程组，通过对该代数方程组进行求解即可得到传热模型的数值解。

3 传热结果分析

通过传热模型计算，得到PMMA墙体受到不同强度热辐射、不同受热时长的软化厚度、热解厚度以及板材中间位置达到软化温度时的温度分布。其中，软化厚度、热解厚度分别指的是在右侧热辐射作用下，达到甚至超过软化温度、稳态热解温度的部分沿厚度方向上的长度。

从图2（左）可以看出，PMMA墙体软化厚度与受热时间成良好的线性关系，即随时间增长软化深度呈线性增长；斜率与热流密度成负相关，即热流密度越大达到相同软化深度所需要的时间越短。相应的拟合曲线表达式见表3，其中曲线的斜率即为软化速率。

图2 PMMA墙体软化厚度（左）、热解厚度（右）与受热时长的关系曲线

表3 PMMA墙体在单侧受火状态下软化深度与受热时间的拟合关系

同样的，热解厚度与受热时长也呈现良好的线性关系。从图2（右）可以看出，随着受热时间增加，热解厚度呈线性增长。直线的斜率与图2（左）上的曲线斜率保持一致。也就是说，在相同的辐射热流作用下，内部节点达到软化温度、热解温度的过程中温度变化趋势保持不变。

图3为PMMA墙体中间厚度处达到软化温度（375.5 K）时沿厚度方向上的温度分布情况。此时在软化温度至热解温度之间的厚度从40mm左右变为10mm左右，而且该区域内的温度梯度随着辐射强度的增加而增大。这也符合材料自身热扩散系数低的特性（表2），PMMA的热扩散系数与空气、水、铁以及玻璃等常见材料相比低1个~2个数量级。此外，PMMA墙体在受到40 kW/m2或60 kW/m2热辐射作用下，由于表面迅速发生燃烧，其内部温度梯度与20kW/m2热辐射作用时相比明显增大，软化向热解转化区明显减小，表明在表面发生燃烧的情况下，PMMA墙体内部温度的提升速率明显增加。

图3 PMMA墙体厚度中点达到软化温度时的内部节点温度分布

在锥形量热仪下开展PMMA墙体单侧受火试验，考察PMMA墙体以验证上述简化后的一维传热模型。采用热电偶测温方法记录表面温度变化情况。图4为20kW/m2、40kW/m2、60kW/m2时PMMA表面升温过程，左图为理论计算结果，右图为试验结果。从图4样品表面升温过程的对比来看，理论计算结果与试验结果呈现相同的变化趋势，在关键时间点的温度值也十分接近，表明理论计算值与试验值的符合性较好。理论计算结果较为准确，相关数值计算模型及方法较为可靠。

图4 样品表面温度的模型计算结果（左）与试验结果（右）对比

4 结论

该文通过建立一维非稳态传热模型，考察了PMMA墙体在单侧受火状态下的温度变化，获取了PMMA墙体软化厚度、热解厚度与受热时长的关系曲线，并且与锥量试验下PMMA样品表面温度进行对比，数值模拟结果与试验结果的基本吻合。