基于地震背景噪声监测山东临沂地区地下水位变化
顾悦 裴烁瑾 梁姗姗 樊春燕 周元泽
1)中国科学院大学,地球与行星科学学院,北京 100049
2)中国地震台网中心,北京 100045
0 引言
大型含水层系统中的地下水常被作为水源,是水循环中的重要组成部分(Kim et al,2019)。地下水质量和水位变化监测主要基于钻孔等定点直接测量(张磊等,2021; 门北方,2018),其成本相对较高,因而可靠的低成本间接手段越来越受到研究人员和生产部门的关注。目前,基于合成孔径雷达(InSAR)、全球定位系统(GPS)或大地测量等方法观测到的变形模式或重力异常调整,可以在区域尺度监测地下水的赋存和水位变化等(Amelung et al,1999;Argus et al,2014;Kim et al,2019; 李嘉等,2020),但是对于科学研究和生产实践,区域性地下水水位变化监测在空间尺度上仍然偏大。
地震波对于地下介质结构的变化比较敏感(Huang et al,2010;Mordret et al,2010;Yeh et al,2013)。降水、河流补给及地下水抽采等对区域地下水调整的影响可以在地震波速结构变化中有较好的反映(Mainsant et al,2012)。固定地震台站连续观测记录可以持续记录非地震的地震动,即背景噪声。连续观测的地震背景噪声互相关函数可用于持续监测地下速度结构的变化(Shapiro et al,2004;Gerstoft et al,2008;Lin et al,2008;Zheng et al,2008;Hadziioannou et al,2011;Brenguier et al,2014; 温扬茂等,2019)。
地震背景噪声测量已经被引入到监测地下水位调整引起的地下速度结构变化中(Kim et al,2019)。目前,国内应用地震背景噪声监测水库水位相关的波速变化情况取得了一定的成果。例如,陈蒙等(2013)运用背景噪声技术对云南省大银甸水库周围波速变化进行研究,发现水位变化与波速变化存在明显的相关性,并认为这种相关性是由水库水体的卸载作用造成的; 安艳茹等(2015)研究了紫坪铺水库区域在蓄水与泄水过程中库区介质的变化特征,表明地下介质的相对波速变化与水位变化存在较为明显的相关性,且在时间上有一定延迟,认为其可能与水的渗透作用有关。
本文基于相对圈闭的临沂地区国家测震台网JUX与JUN台站记录的连续波形数据,利用背景噪声互相关技术研究地下介质波速变化,并结合临沂地区地下水水位和降水等观测数据,分析降水和地下水抽取等诸多因素影响下的地下水位变化与地震波速变化的关系。
1 研究区域及资料选取
山东省临沂地区位于鲁中南低山丘陵区东南部和鲁东丘陵南部,地势西北高、东南低,自北向南有沂山、蒙山、尼山等3条主要山脉,呈NE-SW向延伸,发育沂河与沭河(图1)。区域水系相对圈闭(李致家等,2005),地下水位变化主要由于天然降水和工、农业使用。
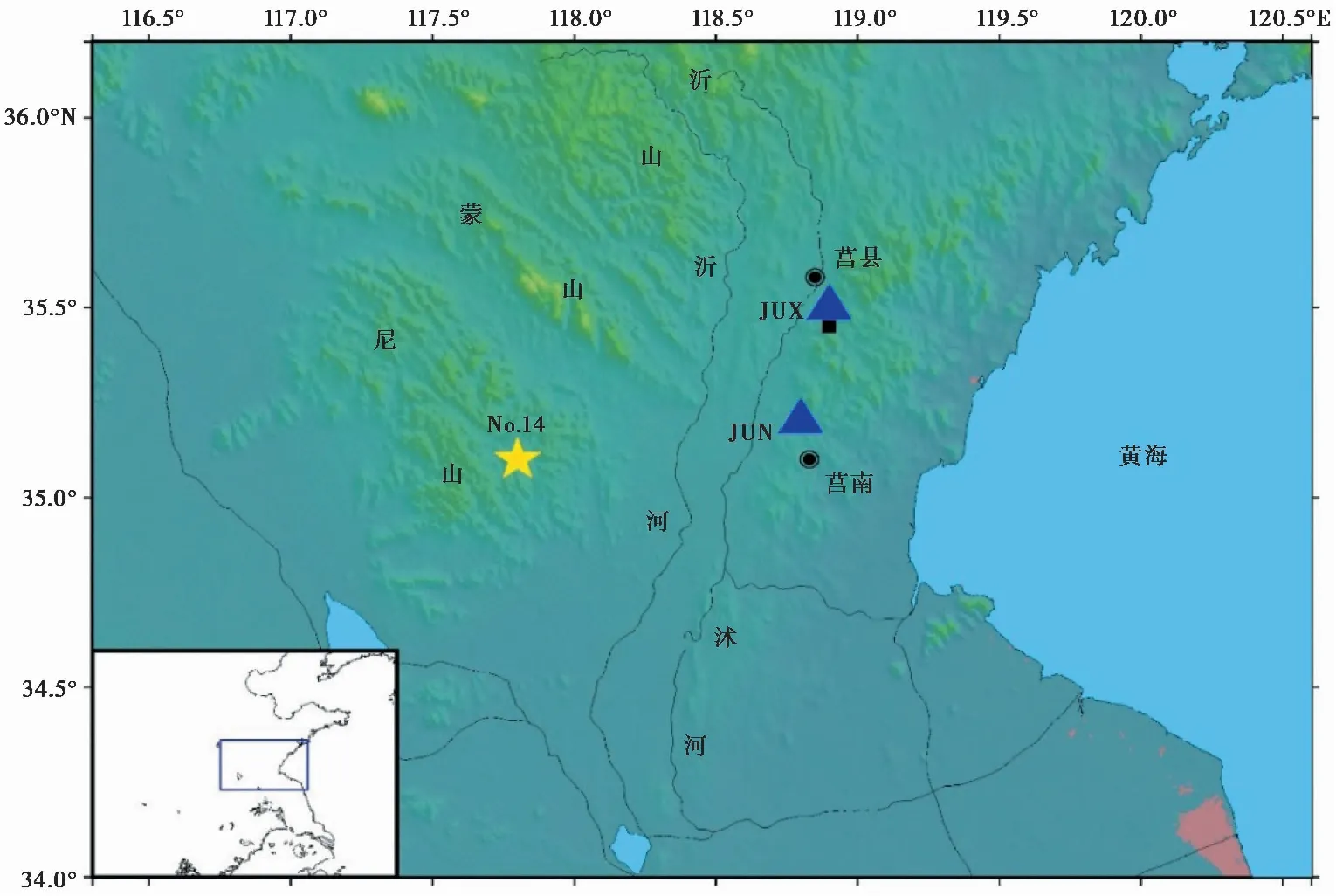
图1 研究区域概况
本地区有国家数字测震台网的多个宽频带地震台、中国地震局地下水位动态监测台莒南鲁14号井以及中国气象局的莒县气象观测站等。本文收集并使用了如下3种类型的数据资料:
(1)地震波形资料为2009年1月1日—2011年1月1日山东省临沂市莒南县的JUN台与日照市莒县的JUX台的连续记录,2个地震台站间距为34.5km。数据资料来自于国家数字测震台网数据备份中心(郑秀芬等,2009),2个台站数据在2009、2010年分别有19天和13天出现缺失或损坏,可用数据的天数总计698天。
(2)地下水水位连续数据来自莒南鲁14号井,该井为研究区内距离最近的与地震监测相关的水井。
(3)日降水数据由莒县气象观测站(编号54936)所记录,数据来自国家气象科学数据中心。
2 地震数据处理
本文使用NoisePy软件(Jiang et al,2020)处理数据,并计算相对速度变化。
2.1 连续记录数据预处理
数据预处理(Bensen et al,2007)主要包括均值和趋势变化去除、波形尖灭、仪器响应去除、带通滤波、时间域归一化及谱白化处理等。具体如下:
(1)为了使数据标准化,进行除均值来去除波形数据本身具有的非零均值。通常波形数据会存在一个长周期的线性趋势,从而影响数据的分析,故需进行去趋势处理。
(2)在对数据进行谱域操作(如FFT、滤波等)时,若数据的两端不为零,则会出现谱域假象,因而实际数据经常需要做尖灭处理,使得数据两端在短时间窗内逐渐变成零值。
(3)为了消除仪器本身的影响,还原真实的地面运动,进行了仪器响应去除。
(4)本文研究的是浅层介质波速的变化,关注相对高频的信息,故选取滤波参数范围为0.1~2Hz。
(5)时间域归一化是数据预处理中最重要的步骤,为了减少地震事件和台站附近非平稳噪声源相互关系的影响,采用一位归一化方法(Derode et al,1999)进行处理,采样频率为10Hz。
(6)谱白化即为频率域归一化,可以拓宽背景噪声在互相关计算中的频带,也可以减小微震信号对计算结果的干扰。
2.2 背景噪声数据的互相关及时间叠加
对2个台站经过预处理的数据进行逐日互相关计算,获得相应的日互相关函数。选择合适长度天数的日互相关函数叠加作为当前互相关函数(CCF),其可表征一段时间的地下介质状态; 叠加整个研究时间范围内所有的日互相关函数,将其作为参考互相关函数(REF),其可表征地下介质的背景状态。
本文背景噪声互相关处理分为如下几个步骤:
(1)将每日波形数据截取为48段,每段30min,每段有50%重叠;
(2)在频率域对2个台站的每段数据进行互相关运算,叠加48段互相关函数作为日互相关函数;
(3)叠加8天日互相关函数作为CCF(图2);
(4)叠加2年所有日互相关函数作为REF(图3)。
由不同叠加天数的互相关函数形态(图2)可以看出,随着叠加天数增加,CCF波形趋于稳定; 而且对比图3,CCF波形趋势变化也更趋近于REF。本文选取8天的日互相关叠加作为CCF,用于后续解算。
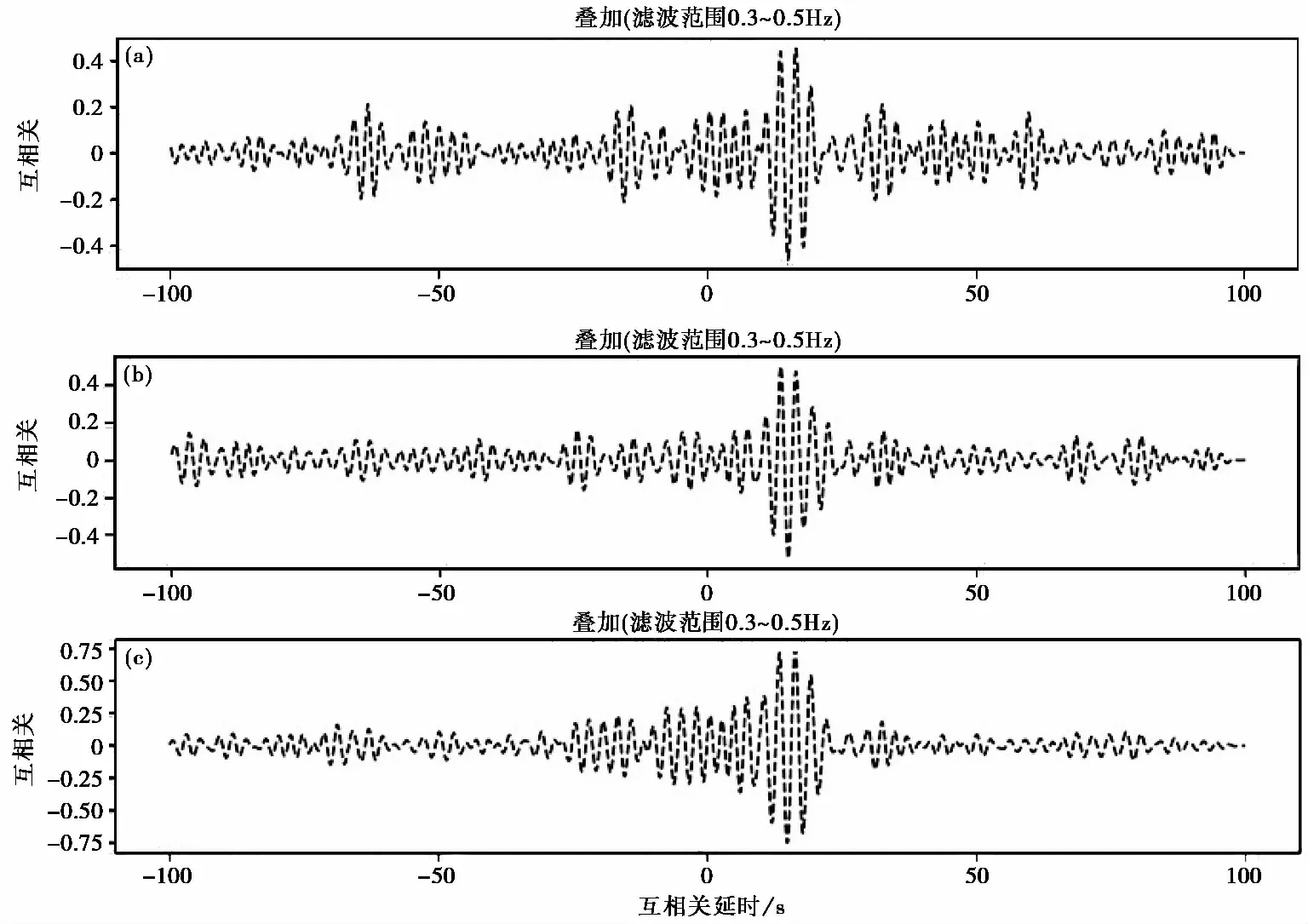
图2 JUN与JUX台叠加不同天数的日互相关函数所得当前互相关函数CCF
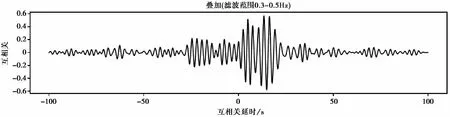
图3 2009年1月1日—2011年1月1日JUN与JUX台参考互相关函数REF
图4给出了2009年1月1—8日,共8天长度的互相关叠加函数CCF与所有天数的REF对比,从中可以看出,两者波形具有较好的相似度。2个互相关波形对称性较弱,正时间段的振幅较高,负时间段的振幅较低,应与噪声源方位性分布有关(Chen et al,2010); 短时间段CCF的噪声源方位性效应更明显。
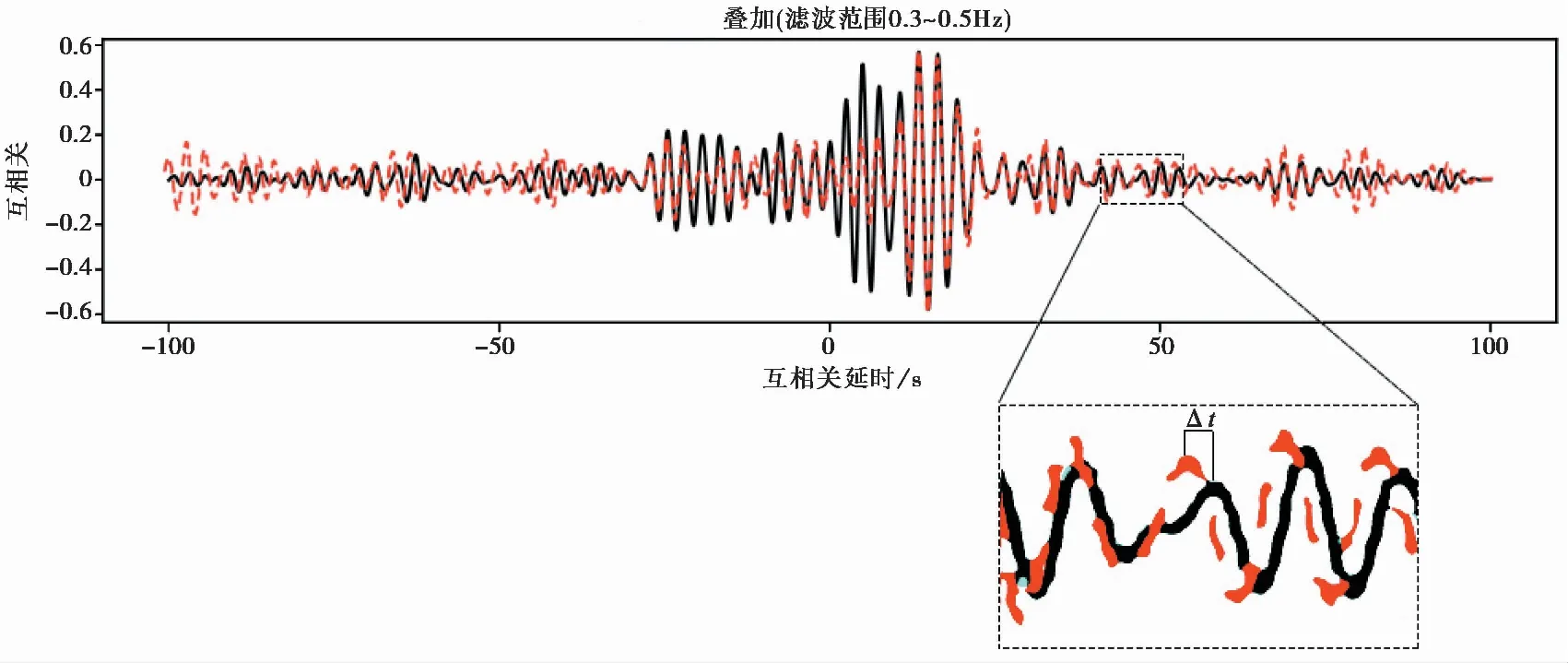
图4 8天与全部698天的日互相关函数叠加所得CCF对比
2.3 到时差提取与相对速度变化计算
由图4 可见,每对CCF与REF波形曲线在不同的时间t上有不同的走时延迟Δt。实际延时提取更多使用谱域方法进行,可以明确相关函数中相关信号的带宽(Poupinet et al,1984),且能够有效提升计算效率。该方法最早被用于研究地震对地下介质影响所引起的相对速度变化。
本文相对速度变化计算使用的是移动窗互谱法(MWCS,Moving Window Cross Spectral)。Clarke等(2011)详细阐述了MWCS方法的原理及步骤,为利用背景噪声研究地下介质状态变化打下坚实基础,本文不再赘述。
2.3.1 计算走时延迟变化
MWCS方法第一步为计算CCF与REF的走时延迟Δt。将每个互相关函数划分为不同重叠的窗口N,进行去平均及尖灭处理,并对CCF与REF分别进行傅立叶变换,则互谱X(f)表示为
(1)
式中,Fref(f)与Fcur(f)分别表示REF与CCF的傅立叶变换,f为频率,*表示复共轭。
走时延迟Δt在互谱中出现于相位谱上,因此将互谱X(f)进一步写为振幅谱|X(f)|与相位谱φ(f)相乘的形式,即
X(f)=|X(f)|eiφ(f)
(2)
式(2)中相位谱φ(f)在离散情况下可以写为
φj=mfj
(3)
m=2πΔti
(4)
其中, Δti(i表示第i个窗口)即为2个波形信号特定时刻t的走时延迟;j=l,…,h。可基于最小二乘加权线性回归法获得的斜率估计m(Clarke et al,2011),有
(5)
其次,计算相关误差em
(6)
(7)
其中,ωj为加权系数,有
(8)
其中,Cj为相关函数振幅谱的归一化相干函数离散值,Xj为互谱离散值。
2.3.2 计算相对速度变化
在一阶近似下,区域内地震速度扰动Δv/v是均匀的,并且表现为CCF相对于REF的拉伸Δt/t(Clarke et al,2011)。这种拉伸在数值上与速度扰动相反(Poupinet et al,1984),即
Δt/t=-Δv/v
(9)
综合考虑台站间距、波的速度、信号的能量强弱等因素,本文选择加载移动窗长为25s,对应于互相关10~35s部分,此部分包含面波及尾波。
3 结果与讨论
3.1 2009—2010年地下介质相对速度变化
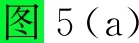
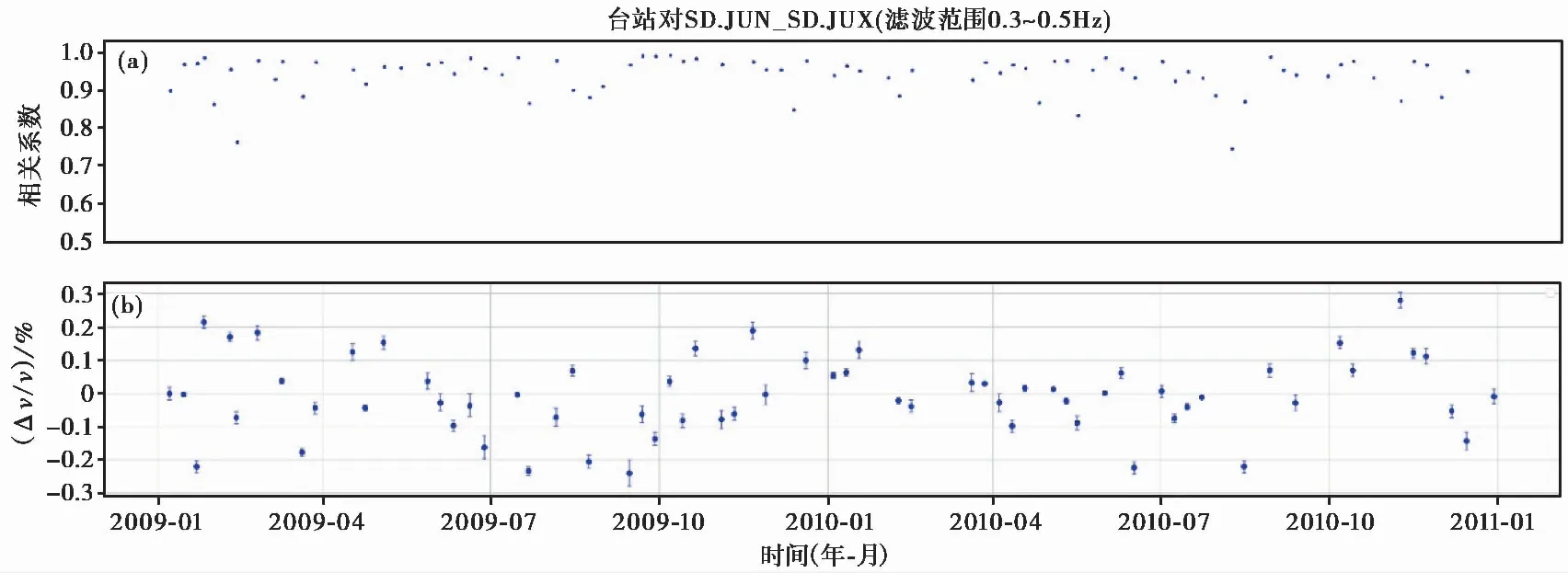
图5 相关系数与相对速度变化
3.2 临近地下水位变化
地下水位数据来自于莒南鲁14号井,按每分钟水位测定记录了2009年1月1日—2011年1月1日的水位值。分别选择每天0点与12点的数据成图,得到地下水水位变化,如图6、图7 所示。
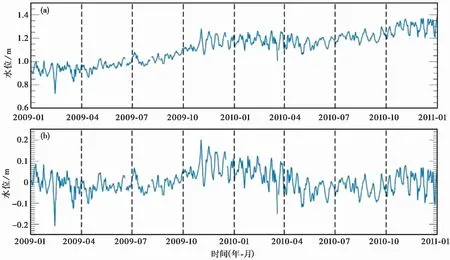
图6 2009年1月1日—2011年1月1日莒南鲁14井水位变化(0点水位值)
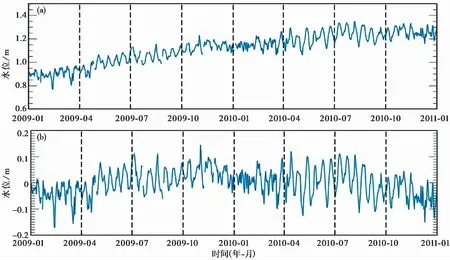
图7 2009年1月1日—2011年1月1日莒南鲁14井水位变化(12点水位值)
由图6(a)可见,水位呈整体上升趋势,但有季节性变化。为了更清晰地看到变化规律,采用最小二乘法对数据进行了去趋势处理。由图6(b)可见地下水水位呈明显季节性变化,2009年4—10月、2010年6—10月地下水水位较低,随时间呈上升趋势; 2009年11月—2010年 5月水位值较高,呈下降趋势。前人对不同地区水位研究也得到呈季节性变化的相似结论,如 Argus等(2014)利用GPS观测方法推断出加利福尼亚总蓄水量随季节变化。
图7可见整体水位仍呈上升趋势,但去趋势后水位季节性变化不如0点明显,认为白天水位变化受人为影响较大,夜间水位较为稳定,误差较小。
为了理解地下水位季节性的变化,统计了莒县日降水量变化。由图7(a)可见,2009年4—10月、2010年4—10月降水量大,其余时间降水量较小; 夏季降水量远高于冬季。与图6(b)对比,认为降水对地下水的影响有一定的滞后性。这里需要指出的是,由于地下水观测点距离地震台站的位置相对较远,降水对地下水位的影响仅具参考意义。
3.3 相对速度变化与地下水水位变化对比
将相对速度变化、地下水水位变化与日降水量变化进行对比,如图8 所示,从中可以发现,三者变化均呈明显的季节性特征。相对速度变化与水位变化呈负相关的趋势,但存在一定的时间上的延迟量,意味着地下水的影响不是即时的。例如,2009年10月—2010年4月水位呈下降趋势,同时间段内速度变化则先上升、后下降。
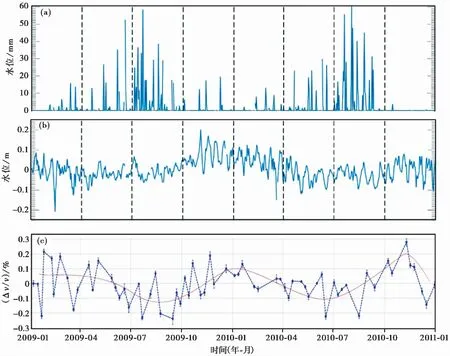
图8 降水变化、地下水水位变化及相对速度变化对比
3.4 其他因素对地下介质速度变化的影响
地下介质速度变化不仅受到地下水位调整的影响,地震孕育过程、地球自转和潮汐效应等均会对其有一定的影响。
一般地震活动相关的介质速度变化更多地体现在地震发生前后(刘志坤等,2010)。临沂地区地震活动性不强,且本文获得的地下介质速度变化体现出季节性特征。
地下水潮汐效应对地下水位变化会产生影响,但是目前的研究表明其周期为6天左右(王学静等,2013),这种短周期效应需要更密集的台网观测才能够给出。
另外,地球自转可以引起地下介质速度变化,但地球自转带来的季节性变化主要来源于太阳辐射光在南、北半球表面上的分布不平衡(宋贯一,2011),这种影响很弱,不足以解释地下水位季节性变化的现象。
4 结论
本文基于2009—2010年的地震背景噪声数据,利用移动窗互谱法计算得到相对速度变化,结合降水和地下水水位监测数据,研究了山东省临沂地区地下介质速度变化与地下水水位变化的相关性。研究结果表明,地下介质速度变化呈季节性,夏季相对速度变化降低,冬季相对速度变化升高; 地下水水位变化亦呈季节性,夏季水位值较低,随后逐渐增加,冬季水位值较高,随后逐渐减少,受莒县降水量季节性变化的影响; 介质速度变化与地下水水位变化呈现此消彼长的趋势。介质速度变化与地下水水位的明确相关性表明,可以基于地震背景噪声对区域水位变化进行监控,从而服务于水资源利用及可能的地质灾害预测。

