基于数据驱动的泥岩速度变化规律研究

刘 振

(中海石油(中国)有限公司深圳分公司,广东深圳518000)

地震岩石物理研究主要关注不同岩性储层的岩石物理模型及相关的储层物性反演问题,如砂岩、碳酸盐岩、缝洞储层、油页岩等。各种岩石物理模型中,WYLLIE等[1-3]基于层状模型假设针对碎屑岩储层提出的时间平均方程受到普遍认可,在油气勘探开发中应用广泛。然而决定地震反射特征的地层除了各种类型储层之外还有以泥岩为代表的非储层,而我们对非储层地震岩石物理的认识有限。对于泥岩速度与泥质含量之间的关系,1992年MARION等[4]基于人工砂泥混合岩石进行了实验研究,结果显示岩石纵波速度在泥质含量达到40%的时候最大,随着泥质含量继续增加逐渐减小。根据该认识,实验条件下泥岩速度随泥质含量增大而减小,但是否符合地下埋藏状态下泥岩的实际情况未见有讨论。基于测井数据的统计结果发现,研究区浅层砂质泥岩速度高于泥岩,深层砂质泥岩速度小于泥岩,与上述认识存在差异,说明在地下埋藏状态下的泥岩速度变化规律更复杂,需进一步讨论。

近年来数据科学发展迅速,代表性的技术有数据挖掘、大数据分析等[5-6],它主张从数据出发,通过数字之间的相关性指导解决实际问题,被认为是继实验观测、理论推演、计算仿真之后的第4类科学研究范式[7]。数据科学在油气勘探开发中得到广泛应用,文献[8-10]将数据驱动或数据挖掘算法应用于油层分类、靶区优选、页岩气勘探等问题的研究中,取得了较好效果;文献[11-12]探讨了油气勘探开发中大数据分析的模式;文献[13-18]对大数据在油气勘探开发中的应用前景进行了思考和讨论。在以往油气勘探开发研究中,“数据科学”方法的应用主要是讨论如何利用数据规律替代理论认识,而对于如何促进理论研究涉及较少。本文将以泥岩速度变化规律问题为例介绍一种利用数据促进理论研究的方法——通过分析初始模型与数据差异的影响因素改进数学模型,使之更符合地质规律,并进一步结合地质认识加深泥岩速度变化规律的机理认识。另外,需要补充说明的是,本文速度指纵波速度,泥岩指泥质含量大于50%的碎屑岩。

1 测井数据驱动的泥岩速度规律研究

油气田勘探开发过程中形成了大量的观测数据,而这些观测数据是复杂多样油藏地质规律以及测量规则的集中体现,在数据量足够的情况下,数据之间的关联性以及差异性可以用于解剖隐藏的地质规律。基于此观点,提出一种数据驱动数学模型进化的研究方法,即在现有认识或假设的基础上,利用数据的相关性逐步优化初始数学模型,将优化后的数学模型与所研究的问题相结合,获得新认识。

针对如何利用数据解剖泥岩速度随泥质含量变化关系,设计了如图1所示的研究流程,主要包括4部分:①根据泥岩的岩石物理假设建立初始数学模型,并根据模型尽量全面地收集或计算与对应地质问题有关的数据并进行规则化;②基于规则化的数据采用相关性算法进行数据关联分析,将其与数学模型对比,获得差异数据;③结合地质认识,将差异数据转化为数学模型的一部分,改进数学模型;④将改进后的模型与地质概念相联系,使之能够表达地质规律,完成模型优化。

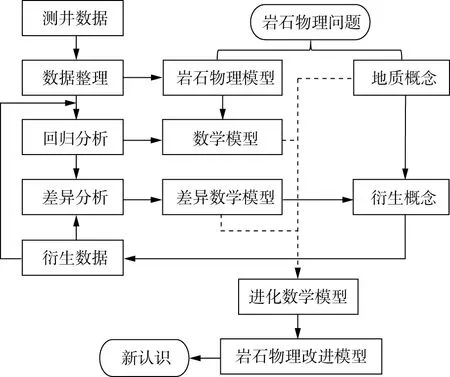
图1 基于测井数据挖掘的泥岩速度变化规律研究流程

1.1 初始数学模型

储层岩石物理研究中已形成了一系列岩石物理模型,被广泛认可和应用的是层状模型,基于该模型进行数学假设,即将泥岩视为砂质和泥质两种成分混合后经过压实和固结的岩石,砂质颗粒和泥质之间相互耦合,遵循时间平均方程:

(1)

式中:v为泥岩速度;vs砂质颗粒速度;vc为泥质速度;φs为砂质含量;φc为泥质含量;φs+φc=1。时间平均方程虽然是针对砂岩储层速度关系提出的一种简单假设,但其对两种成分混合的岩石速度表征是比较准确的,这里以一组简单的数值模型进行补充说明。

1)针对泥岩中砂质和泥质成分按一定比例随机混合的特征,设计网格点为100×100×100的三维数组,数组元素按比例随机赋值为0和1,分别代表泥质和砂质成分。

2)调整0和1数值的比例获得不同泥质含量的岩石模型(图2)。图2a、图2b和图2c分别展示了泥质含量为90%,80%,60%的砂、泥质混合模型,图中黑色样点代表砂质颗粒,白色部分代表泥质。

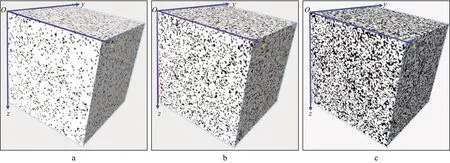
图2 砂泥混合岩石三维数值模型

3)按照泥质含量50%～95%的变化建立一系列砂、泥质混合模型,对0和1分别赋值为泥质和砂质速度获得表征泥岩速度分布的数值模型。

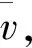
(2)

式中:vi,j,k为模型中x,y,z方向上第i,j,k个网格点的速度;Lz为z方向的宽度;dz为z方向的网格宽度;nx,ny和nz分别为x,y,z方向上的网格点数。

5)同一区域相似沉积背景下砂质颗粒速度比较稳定,而泥质速度受压实作用影响较大,本文取砂质颗粒速度为5 500 m/s,泥质速度为1 600～4 000 m/s,然后分别利用时间平均方程和数值模型计算不同泥质含量、泥质速度相应泥岩的平均速度。

由时间平均方程和数值模拟得到的泥岩速度与泥质含量之间的关系基本一致,如图3a所示,图中圆点表示利用时间平均方程计算得到的结果,叉形点表示利用部分模型计算得到的结果,两者视觉上重合,数值差异小于0.30%(图3b),满足研究精度需求。因此,本文认为时间平均方程用于表征泥质、砂质以及泥岩速度之间的关系是可靠的,并选定为初始数学模型。

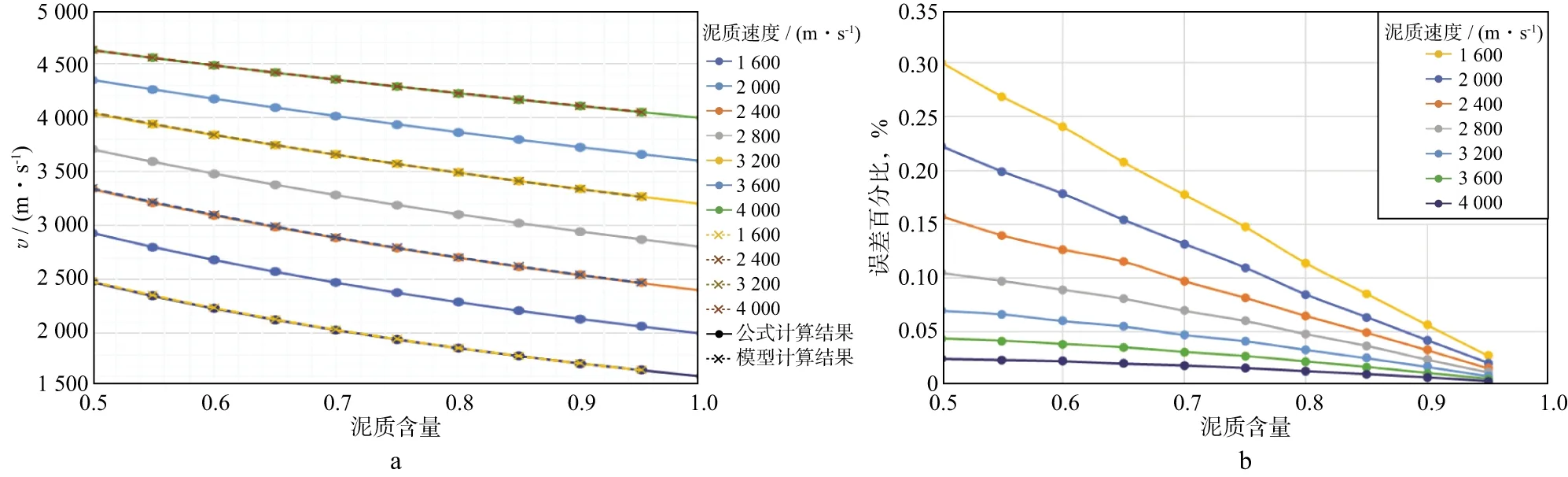
图3 (砂质)泥岩速度随泥质含量变化关系理论计算与数值模拟对比

1.2 数据驱动下的模型优化

根据初始数学模型(时间平均方程)所涉及到的地质参数,选取相关的测井数据作为研究对象,即声波曲线和泥质含量解释曲线,并进行规则化处理和筛选,包括4个方面:①部分钻井声波曲线和解释曲线的采样率不同,基于插值算法将两类数据重采样并对齐到相同深度样点处;②声波曲线一般对应声波时差,将其换算为声波速度;③剔除砂岩、灰岩等其它岩性数据,保留泥质含量大于50%的数据;④为降低埋深对泥岩速度统计结果的影响,同时保证足够的数据量,根据给定深度提取小段(约50 m)数据进行分析。

首先观测相同深度段实测数据特征,选取南海东部HZ,PY,LH,LF等不同油区的探井,提取1 000～1 050 m内的数据进行交会分析,如图4a所示,可见不同钻井之间速度存在差异,但单井速度点均围绕随泥质含量增加而减小的趋势分布,该趋势反映了变量(速度)与自变量(泥质含量)之间的关联特征,即泥岩速度随泥质含量增加而减小,与初始数学模型预测结果一致。

针对单井不同深度区间对应的小段数据,统计分析实际数据与数学模型的差异,结果显示实际数据浅层变化趋势较模型预测更缓,深层与模型预测趋势相反(见图4b)。

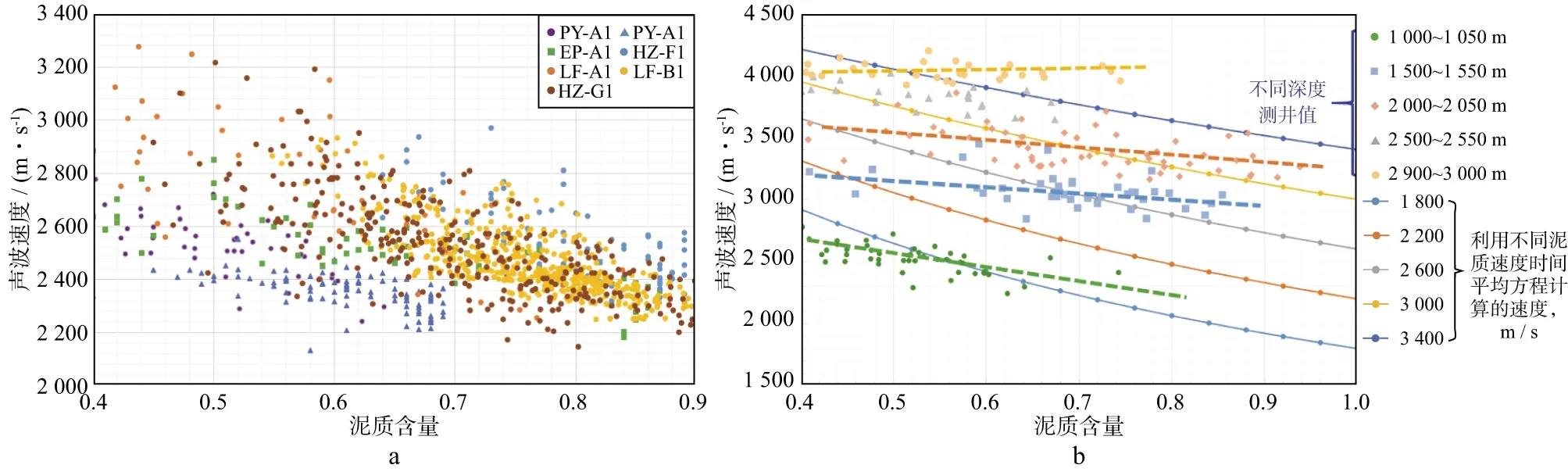
图4 小段钻井数据声波速度随泥质含量变化关系统计

实际数据与数学模型差异的趋势反映了初始模型中未体现的速度变化规律,利用这种趋势指导数学模型优化,有两种思路:①调整基础模型中的部分参数进行重新拟合得到经验公式,该思路在限定区域可解决量化认识的问题;②引入与问题相关的变量,根据差异特征寻找其它影响因素,该思路有助于加深地质认识。本文选用第②种思路,砂质颗粒速度相对稳定,而泥质易于压实、速度变化范围大,故将泥质速度作为数学模型优化的对象,利用时间平均方程将测井声波速度转化为泥质速度。

(3)

继续通过相关性分析解剖泥质速度与泥质含量之间的关系,如图5a所示,可见泥质速度随泥质含量增加而线性增大,线性拟合关系表示为:

vc,z=Kz·φc+X

(4)

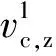
(5)

代入(4)式,得到:

(6)

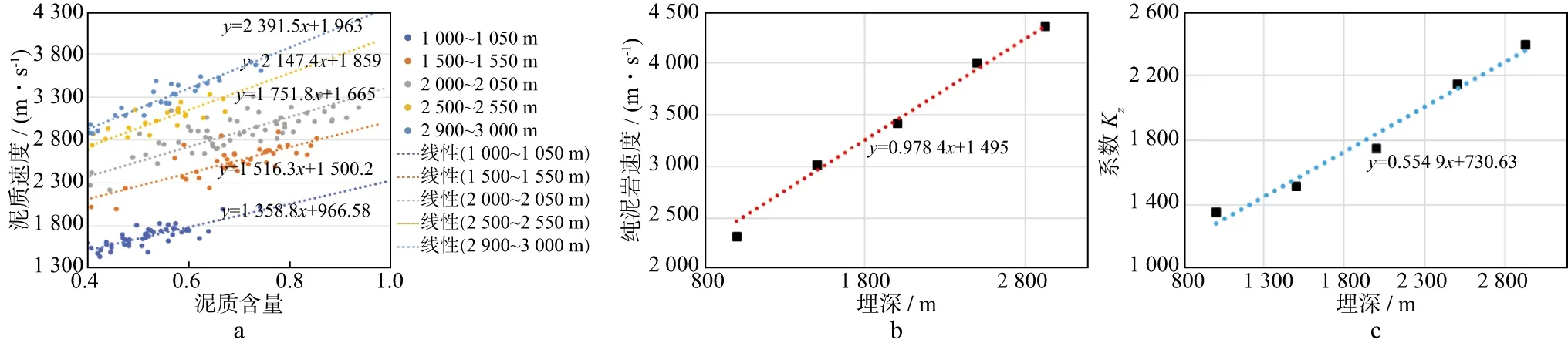
图5 PY-A1井泥质速度规律统计

(7a)

(7b)

(7c)

Kz=C·z+D

(7d)

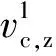
南海东部各区域钻井数据拟合特征基本一致,仅系数A,B,C和D有所差异,如HZ区域的HZ-F1井和EP区域的EP-A1井(图6和图7),可见公式(7)在南海东部具有一定代表性。

图6 HZ-F1井泥质速度规律统计

图7 EP-A1井泥质速度规律统计

1.3 泥岩速度规律认识

进一步收集南海东部HZ,XJ,PY,LH,EP等不同区域共10口钻井的数据进行研究分析,得到一系列泥岩速度、影响系数以及深度数据点,汇总后如图8 所示,拟合得到A,B,C,D的经验值,分别为0.930 8,1 495.2,0.502 9,758.93(注:埋深、速度量纲分别为m和m/s)。该组数值可认为是研究区的平均值,能够反映经验性的规律变化,当涉及到研究区内具体位置时,选用该位置附近井点重新拟合A,B,C,D后对应认识会更准确。

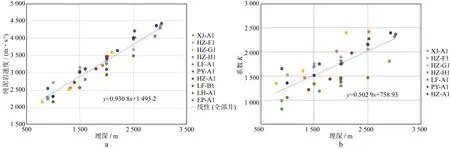
图8 南海东部纯泥岩速度和系数Kz随埋深变化经验关系

结合上述经验值,根据公式(7)可得到研究区泥质速度、泥岩速度随深度和泥质含量变化规律的经验图版,如图9所示,可见对于研究区,①相同埋深下泥质速度变化较大,差异最大可达1 500 m/s;②泥岩速度与泥质含量之间是非线性、非单调性的复杂关系,大致以埋深2 500 m为界,在浅层,砂质泥岩速度大于泥岩,在深层,存在砂质泥岩速度小于泥岩的现象。

图9 南海东部泥岩速度分布经验认识

2 泥岩速度差异压实模型

上述数学模型描述了同一埋深下泥质速度随泥质含量的变化而变化的现象,且最大速度差异在1 000 m/s以上,由于泥质速度反映其压实程度,说明泥质含量不同时,泥质成分压实程度差异较大。本文认为,泥质压实程度的变化并非由泥质本身引起的,而是砂质颗粒,表现在公式(7b)的1-φc,即砂质含量φs。将公式(7)改写为:

(8a)

(8b)

(8c)

Kz=C·z+D

(8d)

式中变量含义与公式(7)相同,公式(8b)中φs系数为负,反映泥岩中砂质含量增加时泥质速度减小。本文认为该现象是一种差异压实作用,即砂质颗粒在压实过程中起到了“支撑”作用,砂质含量增加时颗粒间可压实空间减小,泥质压实程度降低,速度减小,反之亦然,图10为对应的示意图,相同上覆地层压力F作用情况下,随着泥岩中砂质颗粒逐渐减少,岩石截面积逐渐减小、压实程度逐渐增大。

图10 同一埋深下砂质含量不同时泥岩差异压实示意

基于上述认识,认为公式(8)数学模型是研究区泥岩差异压实模型,具体描述如下:①泥岩速度与泥质、砂质颗粒速度之间服从时间平均方程;②砂质颗粒受埋深影响较小,速度相对稳定;③泥质含量为1的泥岩速度(纯泥岩速度)与埋深线性正相关;④砂质含量增大时泥质压实程度减弱,其速度与砂质含量线性负相关,其系数Kz与地层埋深线性正相关。该模型是地质知识化的进化数学模型,有利于加深对研究区有关泥岩速度变化的规律性认识。

3 认识和结论

本文提出了数据驱动数学模型进化的方法,从数据出发对南海东部泥岩速度与泥质含量之间的关系进行了量化研究,探索如何从数据中获取新的油藏地质认识,形成了以下认识和结论。

1)泥岩速度差异压实模型反映了砂质含量对泥岩速度的复杂影响,该模型有利于加深研究区泥岩纵波速度规律的认识。

2)本文方法应用中,引起数据和初始模型差异的因素确定,是改进后数学模型是否能够形成新知识的关键,应充分结合现有理论认识。

3)文中数据的整理和分析主要依赖人工操作,涉及到的数据量有限,结论和认识还存在一定的改进空间。