薛定谔方程在Berestycki-Lions条件下正解的存在性
薛艳昉, 韩建新
(信阳师范学院 数学与统计学院, 河南 信阳 464000)
0 引言
考虑如下薛定谔方程:
-Δu+V(x)u=g(u),x∈Rn,
(1)
其中V:Rn→R是位势函数,g(u):R→R是非线性项。大量的文献在不同的位势下考虑方程(1)解的存在性和多重性。现有文献中,非线性项一般满足经典的(AR)条件、单调性条件或非二次条件等,而这些条件是证明山路结构和(PS)序列有界性的关键。
1983年,BERESTYCKI和LIONS在经典文献[1]中讨论方程:
-Δu=g(u),
(2)
其中非线性项g(s)∈C(R,R)且满足如下条件:
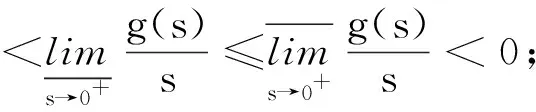
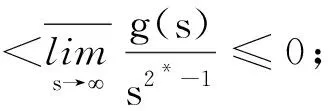
(g3) 存在ζ0>0,使得

上述条件(g1)~(g3)被认为是目前为止,使得方程(2)有解的几乎最弱的条件(以下简称(BL)条件)。该条件引起了诸多学者的兴趣,被众多知名学者从各个方面进行了推广和应用(见文献[2-4])。其中,AZZOLLINI[2]将文献[1]中的自治情形推广到了非自治的情况,即考虑方程(1)解的存在性和非存在性,其位势V满足下面的假设:
(V1)V∈C1(Rn,R)。对任意x∈Rn,有V(x)≥0,且在某个正测集上严格大于号成立;
(V2) ‖(∇V(x),x)+‖n/2<2S,其中S是Sobolev嵌入D1,2(Rn)→L2*(Rn)的最佳常数, 即
(V3)V(x) 径向对称, 即V(|x|)=V(x);

在文献 [2] 中,V(x) 满足 (V1)~(V4) 条件,g(s)满足(g1)~(g3)条件,该文献得到方程(1)解的存在性。受文献[2]的启发,本文也考虑薛定谔方程(1)解的存在性,推广了文献[2]中的相关结果。
1 预备知识
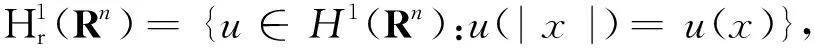
引理2(山路引理) 设E是实的Banach空间,S是E的闭子集,并且将E分成E1、E2两个不同的连通分支。如果I∈C1(E,R)满足下面的山路几何结构:
(i) 0∈E1并且存在ρ>0,α>0,使得I|S≥α>0;
(ii) 存在e∈E2,‖e‖>ρ,使得I(e)<0,
那么存在序列{un}⊂E满足:
I(un)→c≥α,I′(un)→0,
(3)
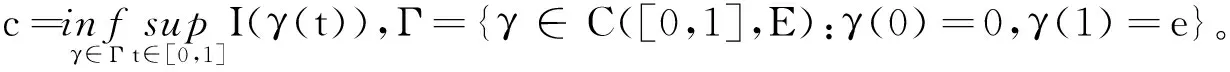
2 主要结果及证明
定理1 若g(s)∈C(R,R)且满足(g1)和(g2),V(x)满足条件(V1)~(V3)以及
(Vg) 存在ζ>0,使得
则方程(1)存在正解。
证明分五步来完成定理1的证明。
第一步,修正非线性项g(s)。
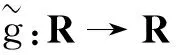
(4)
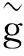
当s≥0时,令
g1(s)=(g(s)+ms)+,
g2(s)=g1(s)-g(s)。
当s<0时,g1(s)=g2(s)=0,则g1≥0,g2≥0且
(5)
(6)
g2(s)≥ms,∀s≥0。
(7)
(8)
根据式(5)~式(8)知,对任意δ>0,存在Cδ>0使得
g1(s)≤Cδ|s|2*-1+δg2(s),
(9)
(10)
(11)

第二步,证明泛函I满足山路几何结构(i)。
根据式(10)、式(11)和Sobolev不等式知,
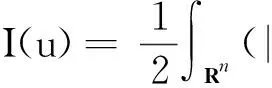


其中0<δ<1。由上述不等式知,存在足够小的ρ>0,当‖u‖≤ρ,u≠0时,有I(u)≥c>0,从而得到泛函I满足山路几何结构(i)。
第三步,证明泛函I满足山路几何结构(ii)。

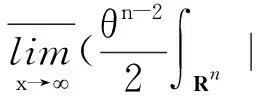

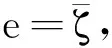
第四步,证明I的每个(PS)序列有界。

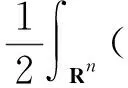
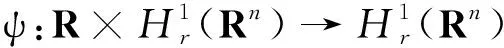
ψ(θ,u)(x)=u(e-θx),
则复合函数I∘ψ为
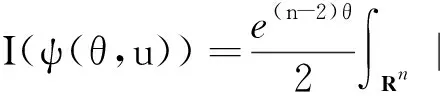
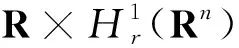
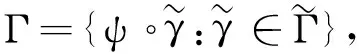

(I∘ψ)′(θn,un)[e,u]=
I′(ψ(θn,un))[ψ(θn,u)]+
J(ψ(θn,un))e。
令vn=ψ(θn,un),则类似文献[6-7]可得,
I(vn)→c,I′(vn)→0,J(vn)→0,
即{vn}是I在临界水平c处的Pohozaev型(PS)序列,也就是

c+on(1),
(12)
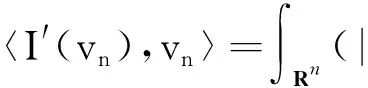
(13)
并且

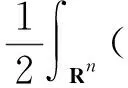
(14)
由Hölder不等式、(V2)和Sobolev不等式得
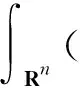
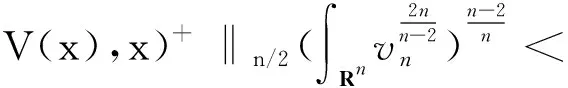
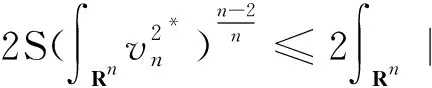
故存在较小的常数β>0,使得
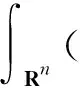
(15)
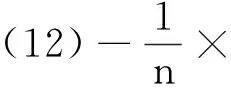
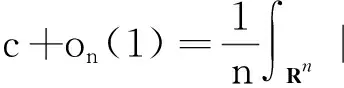


故存在常数C1>0使得
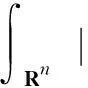
(16)
再由Sobolev嵌入知,存在常数C2>0使得
由式(13)得
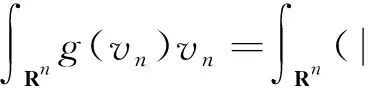
由上式再结合式(9)得
从而有
CδC2。
再由式(7)得
(17)

第五步,证明方程(1)有一个非平凡解。

注记1 与文献[2]比较,文中位势函数和非线性项满足的条件不同。文献[2]中,在径向对称的条件下,通过文献[8]中的单调技巧,得到(PS)序列的有界性,由Strauss引理得到紧性,从而得到正解。此处,借助Pohozaev恒等式,利用山路引理和对称临界原理,得到正解的存在性。
注记2 由文献[5](第2.2部分)知,此处所给的关于g的条件是使得问题(1)有解的几乎最弱的条件。
3 结束语
关于Berestycki-Lions条件下的薛定谔方程的可解性还有很多值得思考的问题,例如:在其他的位势下,如强制位势、周期位势等,是否也能考虑该问题?本文针对的是次临界增长的(BL)条件,对临界增长的情形,是否有类似结论?此外,是否可以类似文献[9-11],针对拟线性薛定谔方程考虑(BL)条件?这些都值得我们进一步地思考。

