功率输入模式对浆果微波加热均匀性的影响

郑先哲，高 明，张雨涵，高 峰，薛亮亮

功率输入模式对浆果微波加热均匀性的影响

郑先哲，高 明，张雨涵，高 峰，薛亮亮

（东北农业大学工程学院，哈尔滨 150030）

提高干燥均匀性是微波技术在食品、农产品热加工研究的重要问题。为分析微波功率输入模式对浆状食品物料的温度及水分均匀性影响，以浆果果浆为高水分、高黏度、富含热敏性成分代表性物料，引入温度离散值、水分离散值、热区分布值、温度对比值指标表征加热均匀性，解析连续和间歇变功率输入模式对浆果微波加热均匀性影响的原因。结果表明：在微波输入功率为800 W的微波加热过程中，果浆中依次出现缓慢升温（I）、温度稳定（II）和快速升温（III）3个阶段，其中温度离散值与热区分布值在升温区增加、在温度稳定区降低；水分离散值持续上升，温度对比值增大至温度稳定区、在快速升温区减小；在浆果微波干燥后期，果浆料层内冷、热点间温度差引起不均匀性减弱。微波在浆果物料边角产生过热效应是引起加热不均匀性主要原因。间歇变功率微波加热工艺可以改善均匀性，随功率转换点的减小，果浆温度离散值、水分离散值、和热区分布值的均匀度改善率增大；微波功率比的减小可提高加热均匀度，但当微波功率比低于0.5时会导致加热效率低；间歇时间的增大可以进一步提高果浆均匀度改善率，但间歇时间超过8 min后对果浆均匀度的改善程度减缓；选用微波功率转换点为第Ⅱ、Ⅲ阶段交界、微波功率比0.5、间歇时间8 min更利于提高加热均匀性与加热效率。研究结果为浆果类物料微波加热均匀性的评价提供数学模型，优化得到的变功率输入参数为提高浆果果浆的微波干燥均匀性提供技术参考。

微波；加热；蓝莓；均匀性；缓苏；变功率

0 引 言

浆果中含有丰富营养物质，尤其是抗氧化能力强的花青素含量高[1]，是典型高水分、高黏度、富含热敏性成分的食品物料[2-3]。微波加热有效率高、可控性强等优点，在浆果的干燥、萃取、膨化、浓缩等热加工过程[4]有较高适用性。但微波加热会使物料内的温度分布差别迅速加剧，导致物料加热不均匀。微波加热不均匀性影响加工效果、能量利用率和产品品质，同时也是解释微波加热机理和优化微波加热工艺关键依据[5]。忽视微波加热不均匀性引起的产品加工品质不稳定和优化工艺适应性差等问题，制约了微波加热技术在食品及农产品加工中广泛应用[6]。

定量表征物料的微波加热均匀性[7]是微波加热条件下解释机理和优化工艺的重要前提。农产品及食品微波加热均匀性的研究热点是机理揭示和工艺优化。微波加热不均匀的本质原因是电磁波在微波腔内壁上反射形成的驻波与入射波产生电场叠加造成强度不同电场分布，分布不均微波进入到微波腔中物料内部，其强度以指数式衰减、且受物料的热特性、介电特性等影响，使得微波加热具有明显的冷、热区分布[8]；通过优化微波强度和料层表观的气流速度等关键参数，获得高均匀度、高品质的浆果果浆微波干燥工艺[9-10]，可提高微波干燥技术适用性[11]。研究微波加热参数与介电物料的交互作用对干燥均匀性的影响，有助于提高干燥品质和能量利用率。选择合适均匀性表征指标是分析微波加热时物料内温度和水分分布的基础和依据。目前通常采用数据点（温度或含水率）间偏差与平均值的比值作为表达均匀性程度的模型[12]，通过计算机模拟、近红外温度检测及图像识别等手段[13]，解析微波加热不均匀性产生原因、建立微波加热参数（模式和工艺等）与物料加热均匀性（微波能吸收、温度分布等）理论模型[14]，从热传递机理上控制温度分布[15]与微波加热过程[16-17]。这些模型计算效率高，可解释性强，但有一定的局限性。偏差与平均值之比只表征三维数据点（位置与温度或含水率）集合中单维度（温度或含水率）上的离散程度，不均匀程度中位置信息没有被纳入模型，这导致模型的信息利用率低，表征方向单一。石欣等[18]基于最大熵原理建立的包含位置信息的模型，提高了信息的利用率，但基于最大熵原理的数学模型对由微波驻波导致的菱角效应和冷热点分布对均匀性影响的表征能力较弱。

微波加热浆果类高水分物料时有明显温度和水分分布不均匀的特征[9]，料层上温度、水分随时间和位置而变化，现有数学模型难以全面反映微波加热物料均匀性的分布与变化。为了解析微波功率输入模式这个关键工艺参数对浆果果浆加热均匀性影响的原因，采用微波功率恒定输入和变量输入对比的研究方法，根据不同功率输入方式下的微波与浆果物料作用及传递特性，确定微波加热均匀性的表征指标，提出浆果类物料的微波加热均匀性评价模型及合理工艺，以期满足微波均匀加热的实践需要。

1 材料与方法

1.1 样品制备

新鲜蓝莓样品由东北农业大学园艺试验站提供，样品均保存在（–20±1）℃的冰箱内。在试验前，将冷冻的物料取出置于室温（25±2）℃下直至接近环境温度，选取成熟饱满、色泽均匀的树莓放置于高速破壁机中（JYL-Y5型，九阳股份有限公司），破碎处理2 min，然后进行搅拌（JJ-1型增力电动搅拌器，江苏省金坛市医疗仪器厂）。制备果浆粒度不大于0.2 mm，初始含水率为88.25%（湿基）。

1.2 试验方法

1.2.1 恒功率微波加热试验

称取（ARRW60型电子天平，美国奥豪斯公司，精度0.0001 g）制备的果浆样品，平铺在矩形微波专用玻璃容器（180 mm×108 mm×72 mm）中，置于微波工作站（MWS，加拿大FISO公司）转盘中心位置，选择微波强度3.5 W/g[10]，即800 W的微波功率下干燥，当果浆含水率低于12%（湿基）时停止干燥，共干燥18 min。干燥过程中每隔2 min，取出试验样品，使用红外热像仪（FLIR E95型，美国FLIR公司）测量料层温度分布，根据烘箱法确定干后样品不同位置采样点的含水率。每组试验重复3次，试验结果用平均值±标准偏差表示。

试验过程中设备及物料的几何尺寸和含水率取样点如图1所示，料层厚度为10 mm。

1.2.2 变功率间歇微波加热试验

通过比较恒功率和变功率两种微波输入模式下果浆加热均匀性的变化规律，解析微波能与物料的作用和体积热在果浆内传递过程，进行与恒功率输入对比的变功率微波输入试验，参数取值选择为表1中带“*”的量。但在微波加热浆果果浆过程中，存在缓慢升温（预热）阶段（I）、温度稳定（起泡）阶段（II）与快速升温阶段（III）；在第III阶段，果浆温度在短时间内急剧升高[19]，易出现焦糊现象，严重时产生热失控[20]。为改善果浆微波加热过程中因第III阶段热失控现象导致的温度水分不均匀现象，在第III阶段中引入间歇变功率工艺，并采用单因素试验方法确定各因素对加热均匀性的影响，因素取值如表1所示。

每次试验开始时称取制备好的果浆样品225 g，按试验条件进行变功率间歇干燥试验，当果浆质量达到含水率12%（湿基）对应的值时，停止干燥。每组试验重复3次，试验结果用平均值±标准偏差表示。

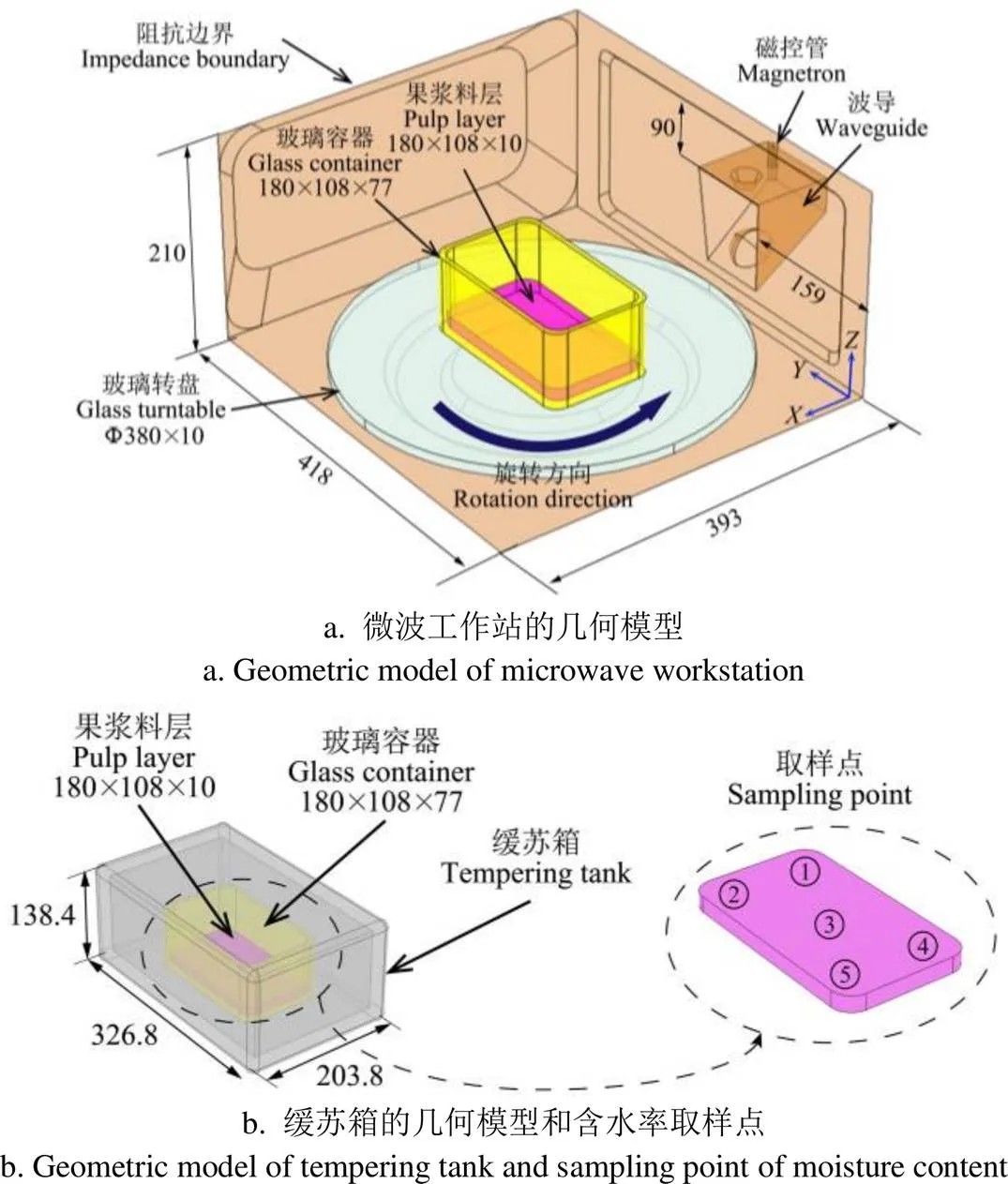
注：尺寸单位为mm。

表1 试验影响因素取值

注：影响因素中“功率转换点”为加入间歇变功率工艺的时间节点，0表示在第Ⅲ阶段中的起始位置加入间歇变功率工艺，40%表示在第Ⅲ阶段中的40%位置加入间歇变功率工艺；影响因素中“微波功率比”为间歇变功率工艺中的微波功率与原功率（800 W）的比值；表中标记*的取值为对其中一个因素进行试验时, 其他2个因素的取值水平,下同。

Note: For the selected factors, the ‘power conversion point’ refers to the time of joining the intermittent variable power process, where 0 indicates the intermittent power conversion process added at the time of the starting stage of III, and 40% indicates the intermittent power conversion added at the time of the 40% of III. The ‘microwave power ratio’ refers to the ratio of microwave power to initial power (800 W) in intermittent variable power process. The value marked * in the table is taken value of the rest factors when one of the factors is tested. The same below.

1.3 水分分布与变化的确定

含水率的测量采用GB5009.3-2010中的直接干燥法。样品的湿基含水率与干基含水率用公式（1）、（2）进行计算[21]:

式中M为湿基含水率，%；M为干基含水率，%；1为干燥前待测样品质量，g；2为干燥后待测样品质量，g。

干燥过程中干燥速率[22]用公式（3）计算:

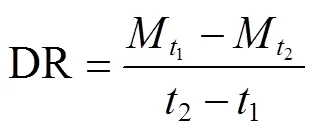
式中DR为干燥速率（干基），%/min；t1为1时刻下的含水率（干基），%；t2为2时刻下的含水率（干基），%；2–1为1时刻至2时刻的干燥时间，min。

为了直接表达物料干后的水分分布，可以通过各取样点的含水率拟合出整个料层的含水率分布图；采用自然邻点插值法[23]，对取样点位置和实测含水率值进行插值，插值点处的数值由公式（4）进行计算：

式中()为插值点处含水率的插值结果，%；f为参与插值的样本点处的含水率值，%；w()为样本点关于处的权重，可以通过公式（5）进行求解:

式中a为参与插值样本点所处泰森多边形的面积，mm2；()为待插点所处泰森多边形的面积，mm2。

1.4 果浆微波加热均匀性评价模型的建立

为全面评价微波加热条件下的不均匀性，从水分数值离散程度、温度数值离散程度、温度局部差异性和热区分布均匀性角度，建立基于微波加热特征的多角度定量均匀性评价模型。

1.4.1 温度离散值(V)和水分离散值(V)

引入“离散值”作为比较各个取样点上数值离散程度的指标。通过对数据进行无量纲的归一化处理，避免不同样本的均值差别引起的误差。对于料层上的温度和含水率值，离散值越大，表明其分布的不均匀程度越高；果浆料层厚度为10 mm，低于微波（频率为2.45 GHz）在常见食品、农产品物料内的临界渗透深度250 mm[24]，因此不考虑微波在料层厚度方向上的衰减及分布，忽略厚度方向上的温度水分差异；物料表面的温度数据通过热成像仪内置软件获取，料层表面不同位置上的温度数值可以使用温度矩阵表达，如式（6）所示。

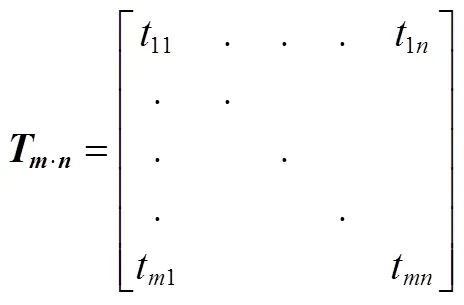
式中T·n为果浆料层表面的温度矩阵；·为红外图像中物料区域中的像素个数，即采集温度数据的取样点个数。t为不同位置上的温度值，℃。

温度离散值（V）通过公式（7）计算[25]:

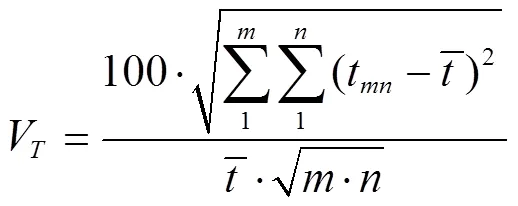
含水率数据通过试验获得，取样点分布如图2所示。水分离散值（V）通过公式（8）计算[26]：

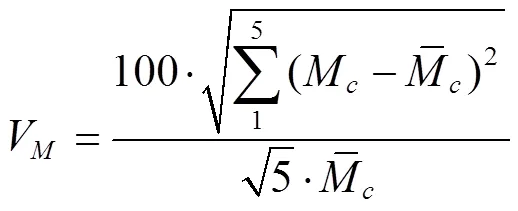
1.4.2 温度对比度值 (CON)

微波加热时，因微波传播特性和热传递规律等影响，引起物料内热点、冷点间的温度差增大，表明温度分布不均匀性加剧。为了评价微波加热过程中产生的局部热点对温度分布均匀性的影响，引入温度对比度（CON）表征局部区域内温度突变程度。

对于级数为的温度矩阵T·n，从最高温度max到最低温度min等分为段，T·n中各元素映射到1到级得到新温度矩阵1m·n。温度共生矩阵TC·L的元素可以表达为式（9）：

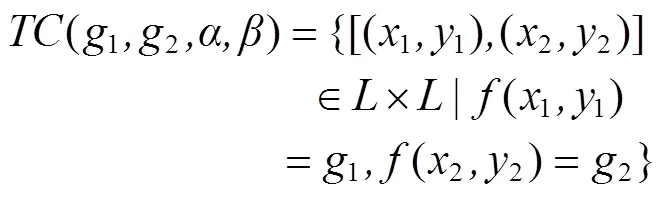
式中(1,2,,)为温度矩阵TC·L中温度等级为1和2元素对的个数；(1,1)为起始点；(2,2)为偏移点；(1,1)为起始点的温度等级；(2,2)为偏移点的温度等级；为偏移点对起始点的偏移量；为偏移点对起始点的偏移角度。

温度对比度值通过公式（10）进行计算：

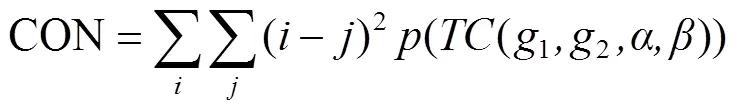
式中((1,2,,))为温度等级为1和2元素对在温度共生矩阵TC·L中出现的概率；为温度等级为1和2元素对在温度共生矩阵TC·L中的行数；为温度等级为1和2元素对在温度共生矩阵TC·L中的列数。

温度共生矩阵的CON值越大，矩阵中元素离主对角线的距离越远，且元素值也越大，表明温度分布中局部热点越明显，温度分布均匀性越差。

1.4.3 热区分布值(HTD)

在微波加热过程中，物料边、角处因微波在不同介质间折射引起电场集中，造成局部的温度过高，产生明显边角效应。采用聚类与热区分布分析相结合的方法，定量分析边角效应对温度分布均匀性的影响。通过对温度的聚类分析确定温度聚焦区，对物料区域分成等面积的个区域（取=10），分别计算聚焦区在个区域中的面积与区域面积的比值，得到聚焦区分布曲线，进而确定热区分布值（HTD）。

1）温度聚焦区的确定

采用K-means聚类法[27]计算温度聚焦区域，对温度矩阵T·n中各元素的温度数值样本集{1,2,3,... ,t*n}，确定最佳聚类数K，任选K个聚类初始中心{1,2,3,... ,a}；对样本集中每一样本t找到距离最近的聚类中心a，并将其分配到该簇中。将分配后各簇平均值作为下一次聚类中心，计算目标函数，重复上述步骤，直至目标函数收敛，输出聚类结果，其中目标函数由式（11）计算得出：

最佳聚类数[27]K由公式（12）得出:

式中为温度矩阵T*n中的行数；为温度矩阵T*n中的列数；为聚类数；avgBWP()为聚类数的评价分数，通过公式（13）、（14）进行计算：

式中BWP(,)表示第类，第个样本的聚类评价分数；和表示类标；(c)表示第类第个样本；(j)表示第类第个样本；(j)表示第类第个样本；n表示第类中的样本个数；n表示第类中的样本个数；||2表示平方欧式距离的计算。

2）温度分布曲线方差的计算

将物料区域等面积分为个区域，温度聚焦区在各个区域内数量与温度聚焦区总元素个数之比为1,2,... ,p。热区分布值HTD由式（15）计算：

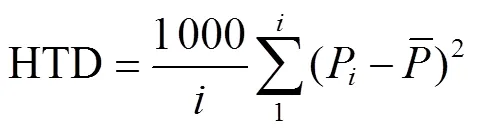
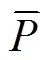
对微波加热浆果料层中的V、V、CON和HTD的均匀性评价指标，根据上述的各自含义和计算过程，确定V(V)是对料层的总体上评价温度（水分）分布均匀程度，反映温度冷点和热点（水分高低区域）分布及变化；CON是评价料层局部区域内温度突变的程度，反映料层内微波体加热引起的热点形成对温度均匀性的影响；HTD反映微波加热时料层边界处温度对整个料层温度均匀性影响。

2 结果与分析

2.1 功率输入模式对果浆微波加热的温度和水分分布的影响

在微波加热过程中，恒功率和变功率输入模式下的果浆料层上的温度分布与水分分布如图2和图3所示。在图2a的温度分布中，随着微波加热过程，果浆料层边缘的温度首先升高，温度聚焦区逐渐向中心区域发展；料层内存在两个温度差别显著的区域：中心区域温度低，其余部分温度高。在图3b的水分分布图中，料层内的水分分布呈现中心高、沿着矩形容器长度方向降低的趋势。对比温度分布图与水分分布图，料层上温度升高与水分降低的区域有较高一致性。

a. 温度分布a. Temperature distributionb. 水分分布b. Moisture distribution

a. 温度分布a. Temperature distributionb. 水分分布b. Moisture distribution

在变功率微波输入模式(功率转换点为40%，微波功率比为0.5和间歇时间为6 min)下，果浆料层上的温度与水分分布如图3所示，由于采用从高到低的变功率输入模式，果浆干燥到含水率低于12%所需时间明显延长，但温度和水分的分布、变化趋势与恒功率的相近，物料的边角温度明显高于中心温度，且这种现象随着时间的增加该现象更加明显，这是由于微波在料层表面的反射、透射以及驻波在微波腔中的传输方式，导致电场在边角区域出现叠加[10]，电场与微波能吸收在料层中呈不均匀分布。在间歇阶段，由于物料温度较高，物料内水分仍在蒸发，这时水分蒸发消耗引起物料降温，且高温位置降温幅度比低温位置降的大，料层中最高温度与最低温度差异逐渐减小。

试验所用微波工作站的矩形腔体（微波波导输入端口在右侧壁）如图1所示。由Fresnel’s定律可知微波传播方向分为横电波（TE）和横磁波（TM）模式。腔体内TE波与料层表面平行的电场，是引起微波热效应的主要波形；而TM波中磁场与料层表面平行，根据Ampere-Maxwell方程（式（16）），磁场引起料层内产生电流，进而在料层内产生热效应。

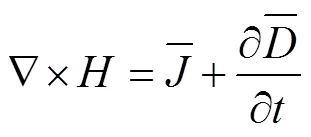
微波腔内TE波的电场和TM波的磁场以与电磁波传递相垂直的方向（方向）从料层边缘侧立面（、面）入射，由低密度介质（空气）进入高密度（果浆）介质，会产生明显反射、散射和非谐振现象[28]，引起果浆料层边缘处产生体积热强度高、而向内剧烈衰减的现象，这是矩形浆果料层边缘处温度先升高的本质原因。阻抗值可以反映入射到物料内电场与磁场转化的程度，与物料的介电常数有关，阻抗值越低表明微波能在物料内转化为热量的程度越高[28]。TE波和TM波入射到果浆内的阻抗值和对比值如式（17）、（18）、（19）所示。

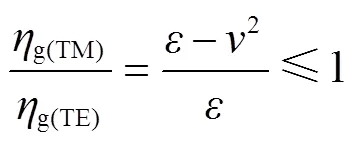
式中g为阻抗，Ω；0为微波在自由空间中传播的阻抗，Ω；为果浆介电常数；为标准化波长。

根据式（19）的结果，微波加热时浆果料层上TM波阻抗值低于TE波的值，表明腔内TM波对浆果料层微波加热起主导作用，因而料层边缘向内部分区域温度高、中心区域温度低。

2.2 功率输入模式对微波加热浆果果浆加热特性分析

浆果果浆类物料在微波加热过程中经历3个阶段[9]，分别为缓慢升温阶段（I）、温度稳定阶段（II）与快速升温阶段（III）。恒功率输入模式的果浆干燥特性曲线如图4所示，在I阶段，果浆平均温度快速上升至70～75℃，平均含水率略微下降，干燥速率小，果浆吸收微波能主要用于温度上升；在II阶段，温度在70～85℃间缓慢上升，平均含水率快速下降，干燥速率快速增大，果浆吸收的微波能主要用于水分蒸发；在III阶段，微波加热试验中果浆平均温度快速上升至155℃附近，平均含水率较快下降，干燥速率逐渐减小。

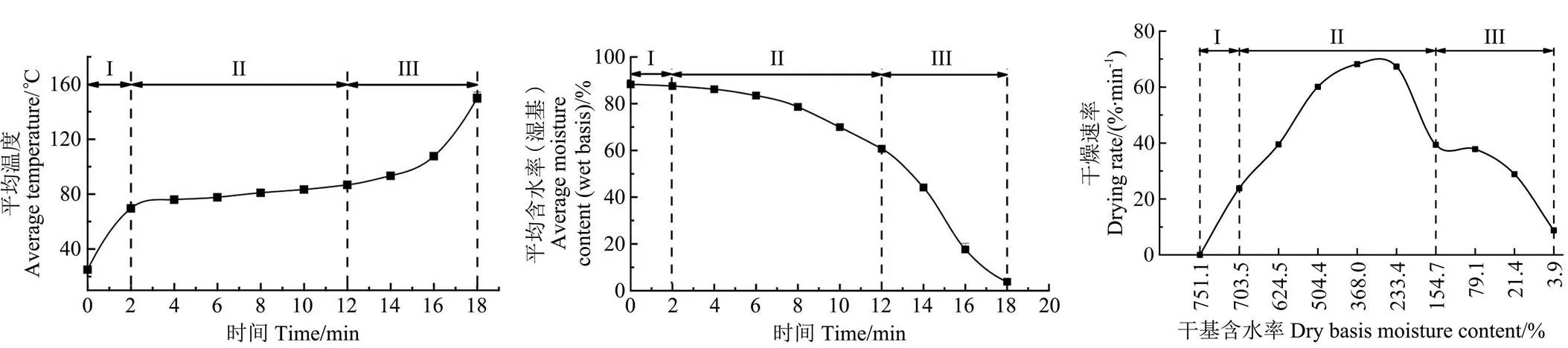
a. 平均温度曲线a. Curve of average temperatureb. 平均含水率曲线（湿基）b. Curve of average moisture content (wet basis)c. 干燥速率曲线c. Drying rate curve

注：I表示缓慢升温阶段，II表示温度稳定阶段，III表示快速升温阶段，下同。

Note:I represents the slow heating phase, II represents the temperature stabilization phase, and III represents the rapid heating phase，the same below.

图4 在恒功率微波输入模式下果浆的平均温度、平均含水率和干燥特性曲线

Fig.4 The average temperature, average moisture content and drying characteristic curve of berry puree under microwave power with constant input mode

微波加热过程中，果浆内部热量产生和传递的规律如式（20）所示[29]：

式中为物料的密度，kg/m3；C为物料比热容，J/(kg·k)；为温度，K；K是物料导热系数，W/(m·k)；是汽化潜热，J/kg；为时间，s；evap为水分蒸发速率，mol/(m3·s)；为微波体积热，W/m3，计算公式如式（21）所示[30]：

式中是微波频率，2.45 GHz；0是空气介电常数；″是物料介电损耗因子；是料层上电场强度，V/m。

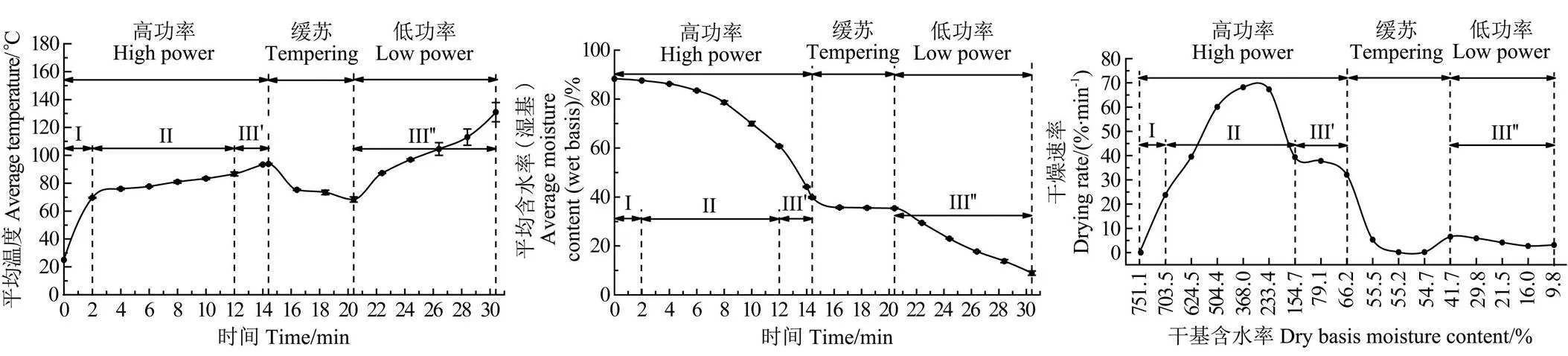
在变功率输入模式下的果浆微波干燥特性曲线如图5所示，由公式（20）、（21）可知，低功率下果浆料层吸收微波能产生的体积热小，温度上升和去水幅度相对缓慢，因此低功率阶段中温度、含水率和干燥速率的变化幅度小于高功率阶段；缓苏阶段中，物料不再吸收微波能，但物料中水分的蒸发耗能仍在进行，因此温度与含水率缓慢下降，干燥速率大幅度减小。在缓苏阶段初期（14～16 min），物料温度较高，水分蒸发速率较大，温度与含水率下降速度较快。而缓苏阶段后期（16～ 20 min），物料温度相对较低，蒸发速率小，温度与含水率下降速度变缓。

在恒功率输入模式下，由式（20）可知，微波传递到物料内部产生体积热，消耗于物料的升温、传热和水分蒸发[11]。在第I阶段，由2.1节所分析的微波与物料接触的入射、衰减、反射作用规律可知，从果浆边缘向其内部呈现由高到低电场强度分布。由式（21）可知，电场强度强度越高产生的微波体积热越多，料层内温度升高程度与电场强度有明显正相关；在微波加热初始阶段，料层内热积累量少，水分缓慢蒸发。随着微波加热过程进行，微波产生的体积热在物料内部积累增加、温度升高，内能增加为料层内果浆中水分蒸发所需的活化能提供更多能量；由于浆果中含有较多的糖分和果胶等成分对水分有较强束缚作用，提高水分蒸发的活化能，果浆内水分蒸发需克服分子间引力及组分束缚力而消耗能量；微波产生体积热使果浆内能积累，当局部果浆内能积累速率与其中水分蒸发能消耗速率平衡时，该区域浆果的温度处于稳定状态。本研究在微波输入功率 800 W、果浆初始质量225 g条件下进行的，物料温度上升至70℃左右，就达到浆果果浆内自由水蒸发的温度条件，果浆内微波热产生量和水分蒸发消耗量形成动态平衡。浆果果浆置于矩形玻璃容器中，在微波加热时，TE表面波被果浆吸收、沿着传递方向衰减[28]，如式（22）、（23）所示，产生体积热逐步减少。

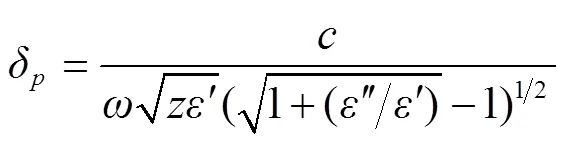
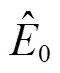
a. 平均温度曲线a. Curve of average temperatureb. 平均含水率曲线（湿基）b. Curve of average moisture content (wet basis)c. 干燥速率曲线c. Drying rate curve

注：III'表示在高微波功率下果浆状态处于第III阶段，III''表示在低微波功率下果浆状态处于第III阶段，下同。

Note:III' represents the pulp in III phase at high microwave power, III'' represents the pulp in III phase at low microwave power, the same below.

图5 在变功率微波输入模式下的平均温度、平均含水率和干燥特性曲线

Fig.5 Average temperature, average moisture content and drying characteristic curve of berry puree under microwave power with variable input mode

在浆果料层内因微波体积热引起内能升高达到水分蒸发所需能量，这部分料层温度维持在某一水平，直到果浆中自由水和部分解脱束缚水全部蒸发，果浆料层的温度再沿着微波传递方向升高；因此果浆料层上存在一个温度稳定的区域沿着传播方向向内移动，直到如图3所示的加热时间8 min，由此可以推断温度稳定区域的存在是由微波强度和物料介电和热特性指标决定的；由于果浆边角位置吸收的微波能大，中心吸收的微波能小，导致物料边缘位置达到微波能和蒸发消耗的热量间的动态平衡的时间低于在中心位置的值，且边角动态平衡温度高于中心温度。随着料层温度稳定区域内水分蒸发，料层内出现气泡（有空气）导致介电特性指标下降，TE波在该区域内衰减程度降低，沿着传播方向传递距离增加，料层中心部分温度升高，如图3中加热时间10～ 18 min所示。微波加热过程中，微波能在物料内吸收直接决定物料温度、水分均匀性[11]。

2.3 不同功率输入模式下加热过程中果浆均匀性指标的变化规律

在恒功率输入模式下果浆加热过程中各阶段对应的温度聚焦区域分布如图6a所示。在第I阶段（0～2 min），果浆边角温度上升，水分因蒸发量少、均匀性较高；在第II阶段（2～12 min），果浆温度稳定区域出现，边角与中心温度差逐渐缩小引起聚焦区分布向物料中心方向扩散，水分不均匀性增加；第III阶段（12～18 min），果浆温度整体快速上升，边角位置吸收微波能高于中心位置，与中心温度差逐渐增大，聚焦区分布向边角退化，因水分蒸发与温度成正比，边角水分快速蒸发，果浆料层整体的水分均匀性下降。

根据图2a、2b和6a所示的果浆料层微波加热过程中的温度和水分变化，其微波加热性指标如图6b～6e所示。V值与HTD值在加热过程中先上升（I阶段）至14.5和5.2附近，随后下降并在11.5和0.9左右趋于稳定（II阶段），最后上升（III阶段）至22.4和5.6左右。这是由温度与聚焦区域分布规律决定的；在整个加热过程中，边角位置水分含量的下降速度持续增大，中心位置水分含量的下降速度缓慢增大，中心与边角间的水分含量之差持续增大，V值在3个阶段（I、II、III）持续增长，最终V值为87.8；果浆料层中蒸发现象在I、II阶段逐渐加剧，电磁波在蒸汽气泡内聚焦产生的局部热点数量增加、温度升高，导致CON值快速上升，达到最大值75.2。在第III阶段起泡现象消失，局部热点通过热传导向周围低温区传导热量，局部区域内温度的突变程度减缓，CON值下降至26.4。

变功率输入模式下加热过程中的温度聚焦区分布和均匀性指标如图7所示。变功率间歇微波干燥结束时的V、V、CON与HTD值分别为18.2、71.1、17.4和5.1，与恒功率微波干燥试验的4个均匀性指标（22.4、87.8、26.4、5.6）相比，均匀性分别提高了18.7%、19.0%、34.0%、8.9%。在缓苏阶段，由于物料内部的热传导、水分扩散和蒸发，盛装矩形玻璃容器内的果浆边角温度降低，局部热点逐渐消失，表现为CON值快速下降（下降幅度15.4），同时V值缓慢下降（下降幅度2.4）。边角与中心水分蒸发速率差减小，显著缓解水分分布不均匀性的发展趋势，V值仅上升1.9。由于局部热点的逐渐消失导致聚焦区分布向边缘退化，HTD值在该阶段上升（上升幅度1.9）；在低功率阶段，V、V与HTD值在总体上呈上升趋势，CON值呈下降趋势，这与恒功率微波加热中第III阶段的均匀性指标的变化趋势一致，但变化幅度减小，这是由于低功率下物料吸收微波能低，体积产生热较少，传热、传质相对较慢，温度与水分的变化小而引起的。

注：VT为温度离散值的改善率，VM为水分离散值的改善率，CON为温度对比度值的改善率，HTD为热区分布值的改善率。

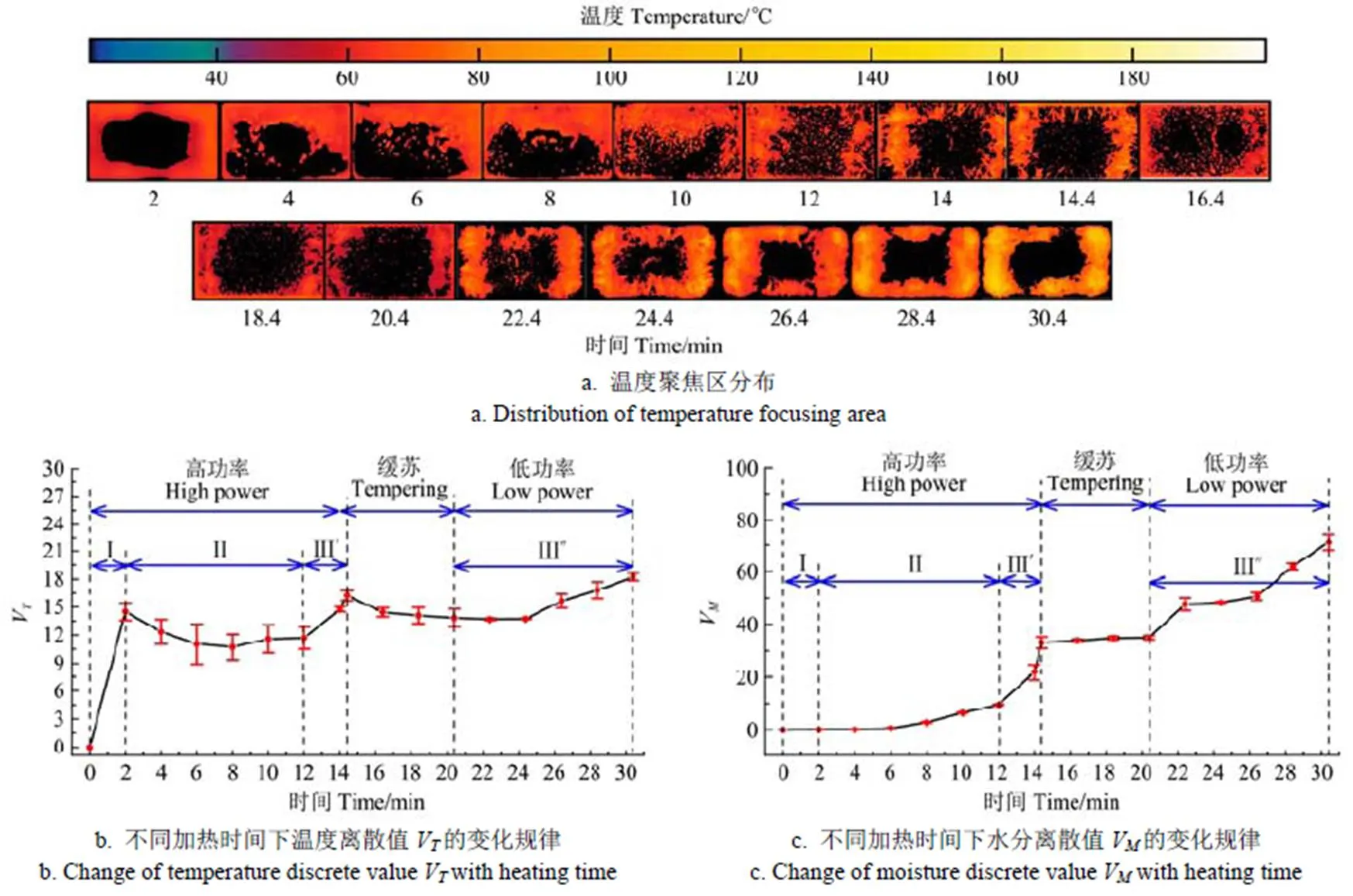
在恒功率输入模式下果浆加热过程中各阶段对最终不均匀性的贡献率如表2所示，第I阶段对最终不均匀性的贡献率均为正值，这是由于微波能迅速在物料中积累引起温度快速升温至平衡温度、导致不均匀性加剧；第II阶段与第III阶段对局部区域内温度的突变程度（CON）的贡献率最大，这与微波加热果浆内的蒸汽气泡的生成、膨胀和消失有关。因此，在微波加热过程中，除了在第II阶段的温度离散值、热区分布值与III阶段的温度对比度值减小外，各阶段中4个指标值均增大。这些结果表明微波在浆果物料边角产生过热效应是引起加热不均匀性主要原因，而果浆内冷、热点温度差对干燥后期的加热均匀性影响减弱。

表2 恒功率加热条件下各阶段对最终不均匀性的影响

2.4 变功率输入模式对果浆微波加热均匀性的影响

间歇变功率工艺中各影响因素对干后果浆的均匀度的改善率如图8所示，均匀度改善率由式（24）计算：

式中UIR为均匀性改善率，%；UIX0为恒功率微波加热条件下的干后均匀性指标；UIX为加入间歇变功率工艺时的干后均匀性指标。

由图8可知，间歇变功率工艺显著降低局部热点引起的温度突变（CON值）。相比恒功率输入的微波加热，间歇变功率工艺可以有效降低整体物料温度，由公式（25）可知[32]，果浆在低温度下蒸发速率下降，整个料层水分蒸发起泡程度相对较弱，微波在蒸汽气泡内聚焦产生的局部热点引起温度突变显著改善。

式中A是指前因子，s-1；T是温度，K；Ea是活化能，J/mol；R是理想气体常数，8.314 J(/mol·k)；cn当前是水分浓度，mol/m3；ceq为平衡水分浓度，mol/m3。

由图6b～6e可知，第Ⅲ阶段中加热时间越长，CON值越小，V、V与HTD值越大。在图8a中，随功率转换点的增加，物料在高功率下的加热时间增长，导致物料在高功率加热阶段终点（缓苏阶段起点）的CON值逐渐减小，而V、V与HTD值逐渐增大。在间歇时间和微波功率比相同的情况下，最终物料的CON值随功率转换点的增大而减小，而V、V与HTD值随功率转换点的增大而增大。即CON值的均匀度改善率随功率转换点的增大而增大、其他指标的均匀度改善率随功率转换点的增大而减小。功率转换点选用第Ⅲ阶段起始位置可使除CON指标外其他指标的均匀度改善率达到最大。随微波功率比的减小，各指标均匀度改善率均变大。这是由于低功率下物料吸收的微波能减少，微波加热引起料层内高、低点温度差缩小，边角与中心位置的温度、水分蒸发速率差异低，由微波在蒸汽气泡内聚焦产生的局部热点引起的温度突变减缓，温度水分分布均匀性增大。表1中微波功率比下的总干燥时间分别为6、7、10、40、80 min，虽然越小的微波功率比对均匀度改善越大，但微波功率比小于0.5，会导致总干燥时间过长、干燥效率低。间歇时间的增大可以提高各指标的均匀度改善率，但间歇时间超过8 min时，改善各均匀度指标率程度减弱。由公式（20）可知，温度梯度与温度随时间的变化率呈正比。在间歇后期，料层内温度梯度小，单位时间内温度变化低，对均匀性的改善程度降低。

对浆果果浆类物料，采用变功率间歇加热的微波加热，如选用0的功率转换点（Ⅱ、Ⅲ阶段交界）、0.5的微波功率比与8 min的间歇时间，既可以提高均匀度，又可以兼顾加热效率。

3 结 论

1）在恒功率条件下的加热过程中，由于电磁波在低密度介质（空气）进入高密度（果浆）介质时产生的反射、散射和非谐振以及热质传递过程中蒸汽气泡的生成、消失，果浆中依次出现缓慢升温、温度稳定和快速升温3个阶段，影响果浆料层的温度分布、水分分布和均匀性指标。其中由电场在料层边角处集中、过热引起的矩形浆果果浆料层内的水分分布非均匀性持续增加；由于果浆内气泡生成与消失，热点温度突变引起不均匀性先增加后减小；温度稳定阶段中物料内微波热产生与蒸发耗能形成动态平衡，边角与中心位置温差减小，温度聚焦区向中心扩散，温度数值均匀性与热区分布均匀性增加。

2）间歇变功率条件下的加热过程中，对温度对比度值均匀度的改善主要在缓苏阶段中进行。但由于物料内部的热传导，中心位置处的热点逐渐消失，导致温度聚焦区的中心区域逐渐消散，热区分布值的均匀性会有所降低。低功率阶段各均匀性指标的变化趋势与恒功率条件下一致，但由于微波能的吸收小，升温与去水速度下降，各均匀性指标的变化幅度低于恒功率条件下均匀性指标的变化幅度。相对于恒功率微波加热，间歇变功率加热中的温度数值均匀性、水分数值均匀性分别提高了18.7%和19.0%。温度对比度值均匀性提高了34.0%，聚焦区在料层中的分布均匀性提高了8.9%。

3）间歇变功率微波加热工艺显著降低果浆中局部热点引起的加热不均匀性。功率转变点越大，温度对比度值的均匀度改善率越大，而其他指标的均匀度改善率越小；随微波功率比的减小，各指标的均匀度改善率增大，但微波功率比小于0.5会导致总干燥时间过大；各指标的均匀度改善率随间歇时间增大持续上升。选择功率转换点为第Ⅲ阶段的起始点，微波功率比为0.5，间歇时间为8 min的间歇变功率工艺参数可以在保证加热效率的前提下最大程度改善加热均匀性。

[1] 刘莹，高涵，王丽霞，等. 红树莓花青素的微波辅助提取研究[J]. 中国农学通报，2018，34(12)：125-131.

Liu Ying, Gao Han, Wang Lixia, et al. Microwave-assisted extraction of red raspberry[J]. Chinese Agricultural Science Bulletin, 2018, 34(12): 125-131. (in Chinese with English abstract)

[2] 郑先哲，刘成海，周贺，等. 黑加仑果浆微波辅助泡沫干燥特性[J]. 农业工程学报，2009，25(8)：288-293.

Zheng Xianzhe, Liu Chenghai, Zhou He, et al. Drying characteristics of blackcurrant pulp by microwave assisted foam matdrying[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2009, 25(8): 288-293.(in Chinese with English abstract)

[3] 姜爱丽，高红豆，胡文忠，等. 高浓度CO2气调对浆果生理及超微结构影响的研究进展[J]. 包装工程，2018，39(9)：96-101.

Jiang Aili, Gao Hongdou, Hu Wenzhong, et al. Research progress of effects of high-concentration CO2modified atmosphere on the physiological metabolism and ultrastructure of berry[J]. Packaging Engineering, 2018, 39(9): 96-101. (in Chinese with English abstract)

[4] 张鹏，颜碧，李江阔，等. 果蔬微波联合干燥技术研究进展[J]. 包装工程，2019，40(19)：16-23.

Zhang Peng, Yan Bi, Li Jiangkuo, et al. Research progress on microwave combined drying technology of fruits and vegetables[J]. Packaging Engineering, 2019, 40(19): 16-23. (in Chinese with English abstract)

[5] 李建硕. 微波加热过程热点与热均匀性控制与优化研究[D]. 重庆：重庆大学，2016.

Li Jianshuo. Research on Hot Spots and Thermal Uniformity Control and Optimization of Microwave Heating Process[D]. Chongqing: Chongqing University, 2016(in Chinese with English abstract)

[6] Zhang R J, Wang Y F, Wang X C, et al. Study of heating characteristics for a continuous 915 MHz pilot scale microwave thawing system[J]. Food Control, 2019, 104: 105-114.

[7] Palazoğlu T K, Miran W. Computational investigation of the effect of orientation and rotation of shell egg on radio frequency heating rate and uniformity[J]. Innovative Food Science &Emerging Technologies, 2019, 58, 102-238

[8] 周明长，李少甫. 基于数值仿真的多馈微波加热温度控制系统[J]. 微波学报，2019，35(5)：92-96.

Zhou Mingchang, Li Shaofu. Multi-feed microwave heating temperature control system based on numerical simulation[J]. Journal of Microwaves, 2019, 35(5): 92-96. (in Chinese with English abstract)

[9] 郑先哲，秦庆雨，王磊，等. 气流改善泡沫树莓果浆微波加热均匀性提高能量利用率[J]. 农业工程学报，2019，35(14)：280-290.

Zheng Xianzhe, Qin Qingyu, Wang Lei, et al. Airflow improves the microwave drying uniformity of foamed raspberry pulp and increases energy utilization rate[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2019, 35(14): 280-290. (in Chinese with English abstract)

[10] 秦庆雨. 树莓果浆连续式微波泡沫干燥工艺研究[D]. 哈尔滨：东北农业大学，2020.

Qin Qingyu. Research on Continuous Microwave Foam Drying Process of Raspberry Pulp[D]. Harbin: Northeast Agricultural University, 2020. (in Chinese with English abstract)

[11] 王磊，沈柳杨，刘成海，等. 微波加热浆果过程中料层电场分布影响能量利用分析[J]. 农业工程学报，2021，37(4)：1-10.

Wang Lei,Shen Liuyang,Liu Chenghai, et al. Analysis of the influence of electric field distribution of material layer on energy utilization during microwave drying of berries[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(4): 1-10. (in Chinese with English abstract)

[12] 步晨. 微波炉仿真与性能提升研究[D]. 成都：电子科技大学，2018.

Bu Chen. Research on Microwave Oven Simulation and Performance Improvement[D]. Chengdu: University of Electronic Science and Technology of China, 2018. (in Chinese with English abstract)

[13] Shi X, Li J N, Xiong Q Y, et al. Research of uniformity evaluation model based on entropy clustering in the microwave heating processes[J]. Neurocomputing, 2016, 173:562-572.

[14] Shen L Y, Zhu Y, Liu C H, et al. Modelling of moving drying process and analysis of drying characteristics for germinated brown rice under continuous microwave drying[J]. Biosystems Engineering, 2020, 195(5): 64-88.

[15] Jain D, Tang J M, Liu F, et al. Computational evaluation of food carrier designs to improve heating uniformity in microwave assisted thermal pasteurization[J]. Innovative Food Science &Emerging Technologies, 2018, 48: 274-286.

[16] Luan D, Wang Y, Tang J, et al. Frequency distribution in domestic microwave ovens and its influence on heating pattern[J]. Journal of Food Science, 2016, 82(1/2/3): 429-436.

[17] Zhang S, Ramaswamy H, Wang S J. Computer simulation modelling, evaluation and optimization of radio frequency (RF) heating uniformity for peanut pasteurisation process[J]. Biosystems Engineering, 2019, 184: 101-110

[18] 石欣，李剑南，熊庆宇，等. 微波加热均匀性评价模型研究[J]. 仪器仪表学报，2014，35(9)：1938-1945.

Shi Xin, Li Jiannan, Xiong Qingyu, et al. Research on the evaluation model of microwave heating uniformity[J]. Chinese Journal of Scientific Instrument, 2014, 35(9): 1938-1945. (in Chinese with English abstract)

[19] 孙宇. 浆果微波泡沫干燥机理与工艺研究[D]. 哈尔滨：东北农业大学，2018.

Sun Yu. Research on the Mechanism and Technology of Berry Microwave Foam Drying[D]. Harbin:Northeast Agricultural University, 2018. (in Chinese with English abstract)

[20] 张志勇，李元强，刘成海，等. 基于“热失控”规律的香菇微波加热工艺优化[J]. 食品科学，2020，41(10)：230-237.

Zhang Zhiyong, Li Yuanqiang, Liu Chenghai, et al. Optimization of mushroom microwave drying process based on the rule of "heat runaway"[J]. Food Science, 2020, 41(10): 230-237. (in Chinese with English abstract)

[21] Zhao Y, Zhang Y, Zhu Y, et al. Optimization of processing technology for blue honeysuckle berry snack: From microwave vacuum concentration to freeze‐drying[J]. Journal of Food Processing and Preservation, 2020, 45(2): e15151.

[22] 朱德泉，马锦，蒋锐，等. 山核桃坚果分段变功率微波加热工艺参数优化[J]. 农业工程学报，2016，32(15)：268-274.

Zhu Dequan, Ma Jin, Jiang Rui, et al. Optimization of process parameters for pecan nut stepwise variable power microwave drying[J]. Transactions of the Chinese Society of Agricultural Engineering, 2016, 32(15): 268-274. (in Chinese with English abstract)

[23] 苑希民，薛文宇，冯国娜，等. 基于自然邻点插值计算的溃堤洪水二维模型[J]. 南水北调与水利科技，2016，14(4)：14-20.

Yuan Ximin, Xue Wenyu, Feng Guona, et al. Two-dimensional flood model of dyke break based on natural neighbor interpolation calculation[J]. South-to-North Water Diversion and Water Conservancy Science and Technology, 2016, 14(4): 14-20. (in Chinese with English abstract)

[24] Ayappa K G, Davis H T, Crapiste G, et al. Microwave heating: An evaluation of power formulations[J]. Pergamon, 1991, 46(4): 1005-1016.

[25] 宋月. 微波泡沫干燥浆果果浆均匀性研究[D]. 哈尔滨：东北农业大学，2018.

Song Yue. Research on The Uniformity of Berry Pulp in Microwave Foam Drying[D]. Harbin: Northeast Agricultural University, 2018. (in Chinese with English abstract)

[26] 秦庆雨，郑先哲，王磊，等. 树莓果浆微波泡沫干燥过程能量吸收与利用[J]. 食品科学，2020，41(15)：124-133.

Qin Qingyu, Zheng Xianzhe, Wang Lei, et al. Energy absorption and utilization during microwave foam drying of raspberry pulp[J]. Food Science, 2020, 41(15): 124-133. (in Chinese with English abstract)

[27] 周世兵，徐振源，唐旭清. K-means算法最佳聚类数确定方法[J]. 计算机应用，2010，30(8)：1995-1998.

Zhou Shibing, Xu Zhenyuan, Tang Xuqing. K-means algorithm optimal clustering number determination method[J]. Computer Applications, 2010, 30(8): 1995-1998. (in Chinese with English abstract)

[28] Erle U, Pesheck P S, Lorence M. Development of Packaging and Products for Use in Microwave Ovens[M]. Duxford: Elsevier Ltd, 2020.

[29] Buttress A, Jones A, Kingman S. Microwave processing of cement and concrete materials–towards an industrial reality[J]. Cement and Concrete Research, 2015, 68: 112-123.

[30] Ye J, Lan J, Xia Y, et al. An approach for simulating the microwave heating process with a slow- rotating sample and a fast-rotating mode stirrer[J]. International Journal of Heat and Mass Transfer, 2019, 140: 440-452.

[31] Sun Y, Xue H, Liu C H, et al. Comparison of microwave assisted extraction with hot reflux extraction in acquirement and degradation of anthocyanin from powdered blueberry[J]. International Journal of Agricultural and Biological Engineering, 2016, 9(6): 186-199.

[32] Law M C, Liew E L, Chang S L, et al. Modelling microwave heating of discrete samples of oil palm kernels[J]. Applied Thermal Engineering, 2016, 98: 702-726.

Effects of input power mode on the uniformity of berry pulp in microwave heating

Zheng Xianzhe, Gao Ming, Zhang Yuhan, Gao Feng, Xue Liangliang

(150030)

Microwave heating has been one of the most popular heating methods for foods and agricultural products. Hence, the core of the material can be heated up rapidly during microwave heating, and then the heat can flow outwards from the core to the surface. Among them, the uniform distribution of heat energy can greatly contribute to the thermal processing of commercial foods in microwave heating. Therefore, this study aims to determine the generation and change mechanism of temperature and moisture distribution in the pulpy food materials under microwave heating. A berry pulp was also introduced as a representative material with high moisture, high viscosity, and rich in heat-sensitive components. Four evaluation indexes were then selected to characterize the even heat distribution of the pulp, including the temperature dispersion (V), moisture dispersion (V), hot zone distribution (HTD), and temperature contrast value (CON). An attempt was also made to clarify the effects of the input power (constant and intermittent variable) modes on the heat distribution inside the berry pulp under microwave heating. The results show that the reflection, scattering, and non-resonance of microwave waves caused the non-uniformity of microwave heating, due to the interference of the low-density medium (air) propagating into the high-density medium (fruit pulp). The microwave volumetric heating inside the berry pulp also resulted in the generation and disappearance of vapor bubbles, indicating a dominated process of the heat and mass transfer. There were three successive stages inside the fruit pulp under microwave heating, including slow heating, stable temperature, and rapid heating. Such variations were then attributed to the uniformity index of the temperature and moisture distribution of the fruit pulp layer. Specifically, the non-uniformity of the moisture distribution inside the berry puree increased significantly, owing to the concentration and overheating of the electric field at the corners of the material layer during microwave heating. By contrast, the rapid change of temperature in hot sites was utilized to weaken the non-uniformity with increasing the temperature and hot zones, due to the formation and disappearance of bubbles inside the berry pulp under microwave heating. These uniformity indexes were used to assess the microwave heating in the berry pulp, where theVand HTD increased in the heating zone, and then decreased in the temperature stability zone, whereas, theVcontinued to rise, while the CON increased in the temperature stability zone, and then decreased in the rapid heating zone. These indicate that the overheating at the corners of berry pulp caused the non-uniformity of microwave heating, whereas, the reduction of temperature difference among cold and hot spots was used to enhance the heating uniformity in the later stage of drying. More importantly, the input power with an intermittent variable mode was used to significantly improve the uniformity of microwave heating inside the berry pulp. Furthermore, the uniformity improvement rate of the pulp,theV,Vand HTD indicators increased, whereas, the CON increased to the stable temperature region (II), and then decreased in the rapid heating region (III), with the increase of the power transition point. Consequently, the heating uniformity was achieved, when reducing the microwave power ratio and the intermittent time higher than 8 min. But, the high-low microwave power ratio below 0.5 was led to the low heating efficiency. Specifically, an optimally variable power input of microwave heating was obtained for the higher heating uniformity and efficiency, where the power conversion point of 0, the power ratio of 0.5, and the intermittent time of 8 min. The findings can provide a potential mathematical model to evaluate the microwave heating uniformity of berry materials.

microwave; heating; blueberry; uniformity; tempering; variable power

10.11975/j.issn.1002-6819.2021.21.035

TS210.4

A

1002-6819(2021)-21-0303-12

郑先哲，高明，张雨涵，等. 功率输入模式对浆果微波加热均匀性的影响[J]. 农业工程学报，2021，37(21)：303-314.doi：10.11975/j.issn.1002-6819.2021.21.035 http://www.tcsae.org

Zheng Xianzhe, Gao Ming, Zhang Yuhan, et al. Effects of input power mode on the uniformity of berry pulp in microwave heating[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2021, 37(21): 303-314. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2021.21.035 http://www.tcsae.org

2021-07-24

2021-09-01

国家自然科学基金项目（32072352）

郑先哲，教授，博士生导师，研究方向为农产品加工与贮藏工程。Email：zhengxz@neau.edu.cn