改进遗传算法求解文化旅游线路规划问题
张瑞姣 陈崇成 黄正睿 方荟




摘 要:针对旅游线路规划问题的非确定性多项式难题(nondeterministic polynomially problem,NP)特性,顾及文化旅游景点文化内涵的多样性,提出了一种可有效保持种群多样性的遗传算法以求解旅游线路规划问题。为了解决传统遗传算法的局部最优问题,改进的算法利用Jaccard系数产生初始种群以提升种群质量;在交叉算子后采用多种变异算子产生多个子代,保留子代与父代中较优个体组成新种群,从而保持种群在进化过程中的多样性。实验结果表明所提算法能够更有效求解旅游线路规划问题。
关键词:文化旅游线路规划;遗传算法;Jaccard系数;变异算子;种群多样性
中图分类号:TP18;K909
文献标志码:A
“自由”旅行方式因其能快速推荐旅游行程,辅助游客决策而广受欢迎。旅游线路规划是旅游推荐领域研究的热点,而旅游线路规划问题(tourist trip design problem,TTDP)则是针对有兴趣访问多个兴趣点(point of interest,POI)的游客的旅行计划问题,需要顾及游客偏好,使其满意度最大化,其本质上是带利益的旅行商问题或者车辆路径问题[1],即非确定性多项式难题(nondeterministic polynomially problem,NP)。定向运动问题(orienteering problem,OP)是TTDP的一个简化模型,是指在限定时间内访问具有相关利润的多个地点,且每个地点只能访问一次,使得推荐的旅行线路具有最大的总利润。针对OP的研究,根据不同的限制条件发展了多种变体,如考虑景点开放时间作为限制条件的带时间窗口的OP问题(OP with time windows,OPTW)[2]等,从而使规划的线路更加符合实际。现有的OP研究大多是面向热门旅游景点,且仅考虑POI的单个属性特征作为景点的利益(如评分最大、距离最小、花费最小等)来构建目标函数,但这并不适用于文化旅游领域。文化旅游中的POI具有许多重要特征(例如文化背景、历史相关性等),这些重要特征是文化旅游的核心竞争力。因此,需要将每个特征的分数范围都与该POI相关联,利用OP建模,为每个POI建模多个分数[3],从而综合衡量POI。
目前,TTDP的求解方法主要包括精确算法、启发式算法和智能化元启发式算法。其中,精确算法虽然能得到精确的解,但其搜索能力较差,只能适用于小规模的POI规划[4]。启发式算法能够在短时间内得到可行解,但解的质量并不高[5]。智能化元启发式算法成为解决该问题的主流算法。元启发式算法包括遗传算法[6]、粒子群算法[7]、蚁群算法[8]、模拟退火算法(simulated annealing algorithm,SAA)[9]等。SAA是一种源于固体退火原理的启发式优化算法,可以较大概率获得全局优化結果,广泛应用于优化问题、旅行商问题等。遗传算法(genetic algorithm,GA)源于达尔文提出的自然进化论的思想,遵循竞争的自然法则和优胜劣汰的生存法则[4],因其搜索速度快、随机性强、过程简单、灵活性强的特点而广泛应用于各个领域,例如组合优化、生产调度等。但GA也存在固有的弊端,种群会在进化过程中因多样性的减少而造成过早收敛问题,也称局部最优问题[10]。因此,保证种群多样性以避免算法陷入局部最优。国内外学者对于上述GA问题的解决研究可大致分为两类:一是提高初始种群质量;二是保持进化中种群多样性等。LI等[11]提出了基于信息熵与博弈论的混合GA(hybrid genetic algorithm,HGA),利用信息熵生成初始种群以提升其多样性,避免算法陷入局部最优解。谭文安等[12]利用混沌理论在GA初始种群获得更优秀的初始群体, 从而提高算法效率。SUN等[13]提出了利用余弦相似性理论对相邻种群间的多样性和相似性进行限定,通过对交叉和变异概率的自适应调整,保持进化过程中的种群多样性,提高算法的收敛和全局最优解。WANG等[14]提出了基于多子代的GA(multi-offspring genetic algorithm,MO-GA),利用多个交叉算子产生多个子代种群以提高种群子代的多样性,解决旅行商问题,使得可行解更加接近最优解。王福林等[15]利用两点交叉算子产生多子代保持种群遗传进化中的生物多样性,提高遗传算法的收敛速度。XIN等[16]利用多子代战略,在传统遗传算法之后增加多域倒位遗传算子,解决旅行商问题,显著提高种群多样性,提升算法收敛和鲁棒性。
本文在上述研究的基础上,提出了改进的GA以求解文化旅游线路规划问题。首先,根据景点的文化属性构建旅游线路规划模型;其次,利用Jaccard系数和多变异算子提升GA的初始种群和进化中种群的多样性,避免算法的早收敛问题;再次,以长征景点中遵义会议为例,对比提出算法与GA求解模型,证明了所提算法的优越性。
1 文化旅游线路规划模型
本文借鉴OPTW,即在OP的基础上考虑POI的到达时间要在景点的时间窗之内,公式如下:
Topentime≤Tarrivetime≤Tclosetime (1)
若Tarrivetime=Tclosetime,则游客不能充分游览景点造成旅游体验差。因此,本文将到达时间与游览时间相加得到游览完景点的时间点,使其不得超过景点关闭时间,并以最大化综合线路评分为目标函数。
1.1 问题描述
由于景点文本中干扰信息多,涉及文化信息的较少,常用的文本挖掘方法会造成挖掘结果精度不准的问题。为此,本文采用正则表达式来精确表征一组字符串[17],并以具有重要意义的长征文化为例,通过红色旅游构成要素[18]及长征文化特点,确定待挖掘景点的文化特征,包括人物、事件和类型(如红军亭、红军桥等)。利用HanLP工具对文本进行分词,然后预定义文化特征,利用正则表达式将景点与特征精确匹配。
模型顾及多种限制因素,包括游客需求和景点属性,其中,游客需求包括游客偏好、起始位置、旅行天数;后者则包括景点的经纬度、文化特征、开放时间、评分、游览时间。为了便于数学模型构建,对模型涉及的问题进行描述,模型涉及到的符号及其含义见表1。
定义1 景点信息。对于每一个景点SiS,Si={tt,l,to,tc,w,r} ,其中r为景点标签集合,r={rp,re,rl},便于游客选择感兴趣文化主题或景点文化类型。
定义2 POI集合s。s是指游客选择了感兴趣的r后产生的POI集合,s={s1,s2,…,sn},其中n表示集合中POI的数量。
定义3 交通时间ttr。ttr为两部分,分别是ttru和ttrs。对于线路c={s1,s2,…,sk},k=1,2,…,n,k≤n,则
ttru(ps,si)=D(ps,si)v(2)
ttrs(si,sj)=D(si,sj)v(3)
ttr(ps,si)=ttru(ps,si)+∑k-1i=0ttrs(si,si+1)(4)
定义4 景点到达时间ta。ta对于不同时段的景点有不同的数学表达式。对于多日旅程,旅行第一天选定的第一景点的到达时间如式(5)所示,其余旅行新一天中第一个景点的到达时间如式(6)所示,其余ta则参照式(7)。
ta(si)=ts+ttru(ps,si)(5)
ta(si)=ts+ttrs(si,sj)(6)
ta(sj)=ta(si)+ttrs(si,sj)+tt(si)(7)
定义5 游客总旅行时间T。T由游客的交通时间和景点游览时间组成,对于线路c={s1,s2,…,sk},k=1,2,…,n,k≤n,则
T=ttr(ps,si)+∑ki=1tt(si)(8)
定义6 景点综合评分sw。sw由两部分组成,即景点评分和景点文化特征,分别对两者进行归一化处理即可得到景点综合评分,其中景点文化特征需要每个特征按归一化过程处理。
sw(si)=w(si)-wminwmax-wmin+rp(si)-rpminrpmax-rpmin+
re(si)-reminremax-remin+rl(si)-rlminrlmax-rlmin(9)
式中:wmin、rpmin、remin、rlmin分别表示Si中评分、人物、事件和文化类型的最小值;wmax、rpmax、remax、rlmax分别对应上述最大值。
定义7 线路综合评分Z。Z即线路包含的景点的综合评分之和。若对于c={s1,s2,…,sk},k=1,2,…,n,k≤n,则c的线路综合评分为
Z=∑ki=1sw(si)(10)
1.2 OPTW模型
OPTW模型以综合线路评分为目标,充分考虑游客偏好、旅游时间等因素,从而求解更为合理的旅游线路。OPTW数学模型可以表示为
Max Z=∑ki=1sw(si) (11)
s.t.T<d×t(12)
h(si)=1, si游客已游览
h(si)=0, si游客未游览 (13)
to(si)≤ta(si)
ta(si)+tt(si)≤tc(si) (14)
ttru(ps,si)<C,C为常数(15)
D(ps,sj)=D(si,ps)
D(si,sj)=D(sj,si) (16)
其中:式(11)表示模型的目标函数;式(12)表示T要满足游客的旅行总时间要求;式(13)表示对景点是否游览标注;式(14)表示更为严格的时间窗控制;式(15)表示游客从起始位置到首个景点的交通时间应在某个时间段;式(16)表示一个假设条件,即景点间的往返距离一致。
2 遗传算法改进
2.1 进化策略
2.1.1 初始化种群产生方式的改进
Jaccard相似系数可用于比较有限样本集之间的相似性和差异[19]。本文引入Jaccard相似系数产生初始种群,利用Jaccard相似度得到个体间的相似性,然后通过Jaccard距离计算个体间的差异。Jaccard相似系数为
J(pi,pi+1)=|pi∩pi+1||pi∪pi+1|,(1≤i≤M-1)(17)
Jaccard距离为
D(pi,pi+1)=1-J(pi,pi+1)
=|pi∩pi+1||pi∪pi+1|,(1≤i≤M-1)(18)
式中:pi、pi+1分别为初始种群中的个体;M为种群规模。个体间的Jaccard距离与Jaccard相似度相反:J(pi,pi+1)越大表明个体间基因的重疊率越高,个体越相似,反之则差异越大;而D(pi,pi+1)越大,表明个体间差异越大。
2.1.2 多子代策略
根据WANG等[14]提出的多子代策略,在交叉算子后增加多个变异算子产生多个子代个体,从父代与子代个体中选择适应度最好的个体组成新种群。突变算子是一种维持从一个种群到下一个种群的遗传多样性的操作[20],则多个突变算子可以增加种群多样性。本文选择常用的3种变异算子:倒位变异、多次交换变异和插入变异。其中,倒位变异是指两变异位置之间的基因倒序排列得到子代的过程;多次交换变异就是多次进行交换变异操作,以p1=[1,2,3,4,5,6]两次交换变异为例,第一次交换2、4,则得到p2=[1,4,3,2,5,6],第二次交换1、6,则得到最终变异p3=[6,4,3,2,5,1];插入变异是将第2个变异位置的基因插入第1个变异位置基因之后。
2.2 算法流程
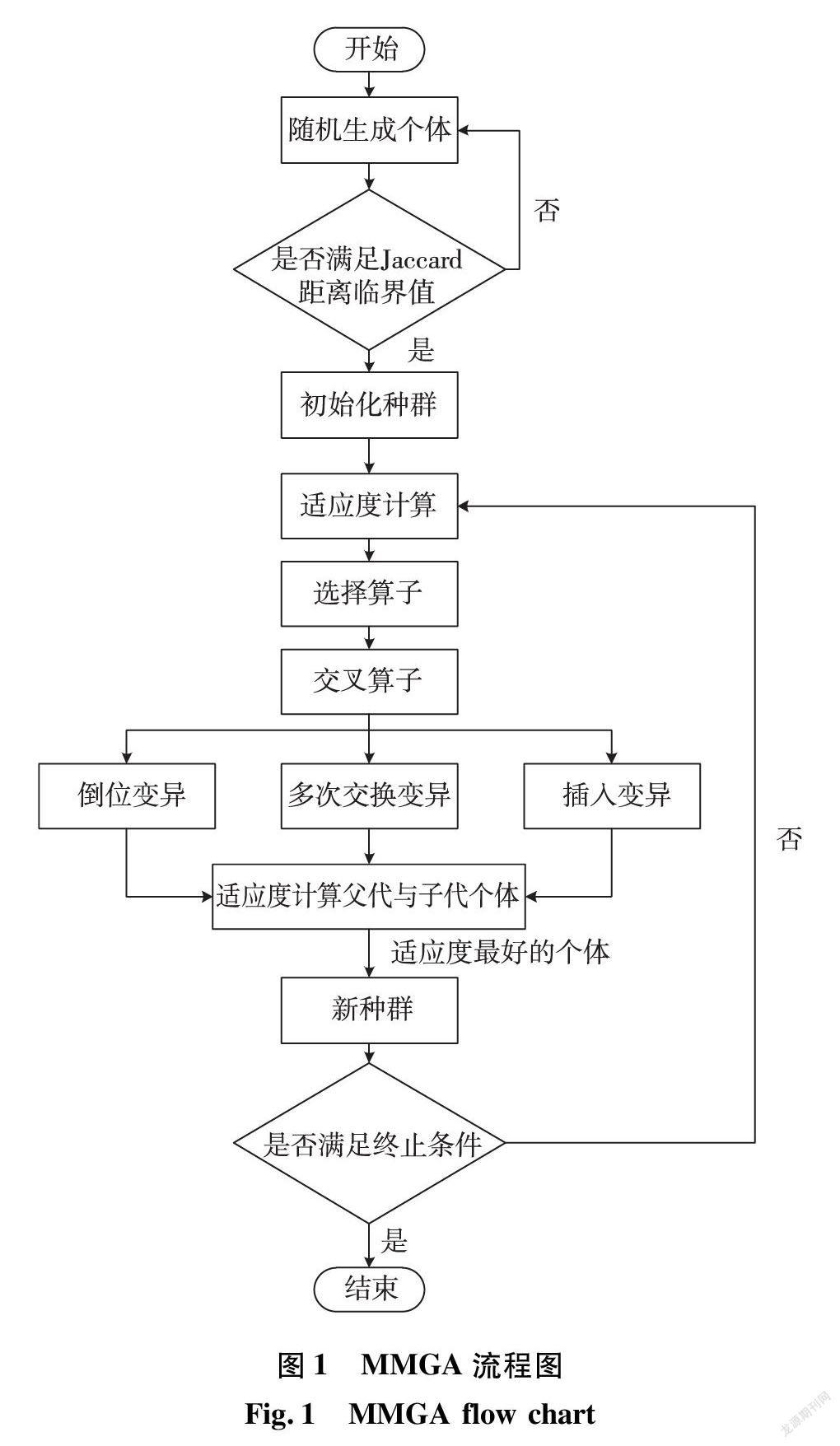
综上所述,本文提出了多变异算子的遗传算法(Multi-Mution GA,MMGA),算法的流程图如下:
MMGA的具体步骤如下:
步骤1 初始化种群生成。利用Jaccard产生初始种群,产生过程如下:
1)设定临界距离H0。
2)使用随机方法产生第1个个体。
3)用同样的方法生成之后的个体,同时计算新产生的染色体与种群已有个体的Jaccard 距离H。如果满足H>H0,则该个体添加到新种群;否则,重新生成新的个体,直至满足H>H0。
4)重复步骤3,达到设定的种群规模M即可得到初始种群。
步骤2 适应度评价。适应度评价是根据目标函数式(11)和各种限制条件,计算个体中满足约束条件的POI,求解适应度。
步骤3 采用赌盘选择法选取M(种群规模)个个体组成种群进行之后的交叉操作。
步骤4 采用类似于顺序交叉的方式,随机产生2个交叉点,将一个体基因的第3部分作为开始,将另一个体去除重复的基因依次插入之后产生一个子代个体,同样的方式产生另一子代个体。
步骤5 采用倒位变异、多次交换变异和插入变异对父代个体进行变异操作,产生3个子代个体。
步骤6 计算步骤5产生的子代个体和父代个体的适应度,并选择其中适应度最大的个体组成新的种群。
步骤7 判断是否满足遗传进化终止条件。本文将最大进化代数设为终止条件,若进化代数小于进化代数最大值,则返回步骤2继续执行;否则,算法结束,输出适应度最好的个体(即可行解)。
3 实验设计与结果分析
3.1 数据介绍与案例说明
3.1.1 数据介绍
长征是1934—1936年中国共产党领导的中国工农红军第一、二、四方面军和红二十五军分别从各根据地向陕甘地区进行的战略大转移,其铸就的长征精神和文化是我国优秀文化和爱国精神的重要组成部分。长征跨越地域范围广,沿途旅游资源较为分散。
长征旅游景点数据以田竞等[21-25]的《重走长征路》系列图书为数据源收集景点数据,辅以望路者旅游网站、百度百科、文献等的景点文化信息,共得到376个景点数据。对长征旅游景点等级状况进行统计,其中,国家4A级和5A级景点的数量分别为26个和4个,国家级文物保护单位70个。长征景点简介信息是由景点的位置、基本情况及涉及的长征人物、时间等组成的文化文本,以福缘桥景点为例,如图2所示。线路规划时需要考虑景点的相关属性信息,则景点所含信息见表2。
3.1.2 案例说明
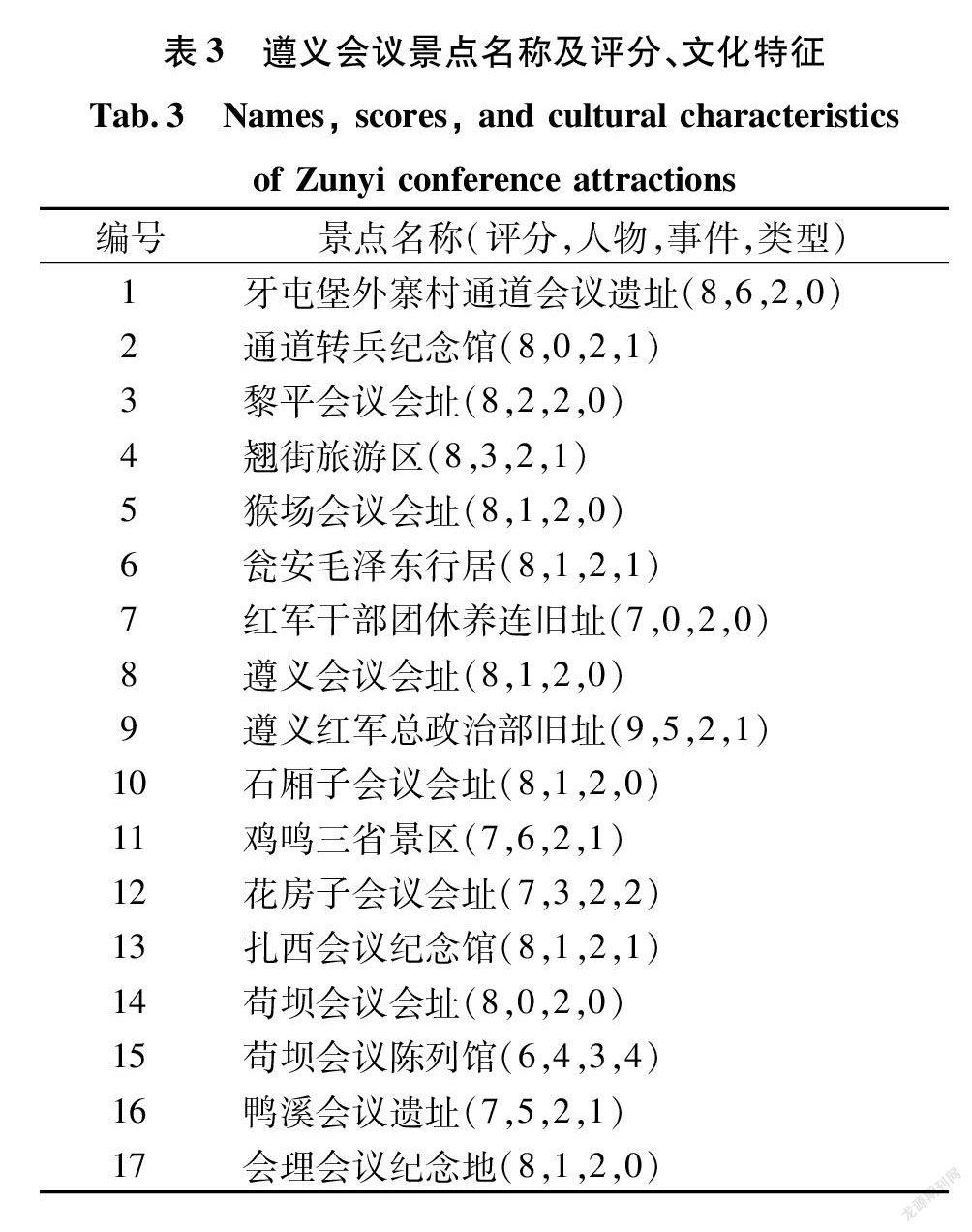
以游客偏好为遵义会议的事件文化特征为例,与之相关的景点不只是遵义会址、红军总政治部。遵义会议是个历史过程,其前后会议如通道会议、黎平会议、会理会议等可看作遵义会议的系列会议[26],因此,这些会议也是遵义会议事件标签的组成部分。此标签集中分布在云贵川的交界区域,地理跨度较小,共包含17个景点,景点名称及对应评分、人物、事件、类型见表3。
3.2 实验与结果分析
3.2.1 实验环境与参数
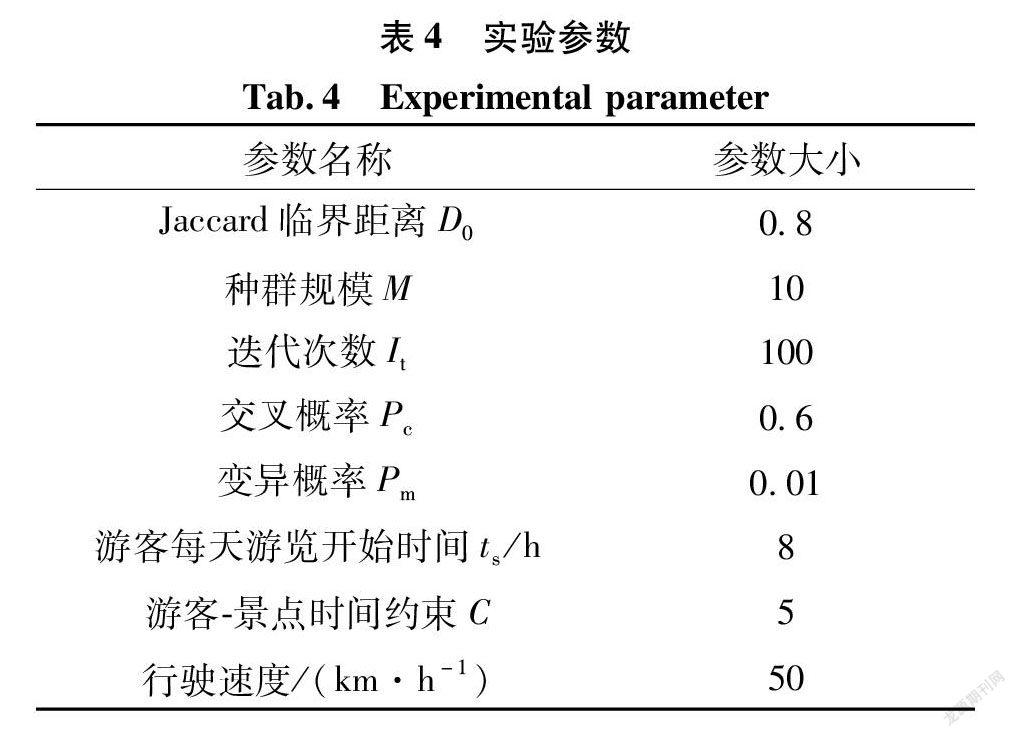
实验是在CPU为Intel(R)Core(TM) i7-4700 3.40 GHz、内存为32 GB、操作系统为 Windows 7旗舰版的 PC 机上进行。算法基于Eclipse软件平台,Java的版本为1.7的环境实现,使用到的工具包包括HanLP等。实验参数见表4。
3.2.2 实验结果与分析
为了验证MMGA的优越性,将MMGA与传统GA以及SAA进行比较,以线路的综合评分为评价指标。实验分为两部分:一是相同旅行天数不同时间约束对比,二是相同时间约束不同旅行天数对比。每次算法得到的线路综合评分略有不同,因此每组实验运行100次,取平均值得到每组线路的综合评分。其中,游客的起始位置设为遵义会议火车站。
1)相同旅行天数不同时间约束对比
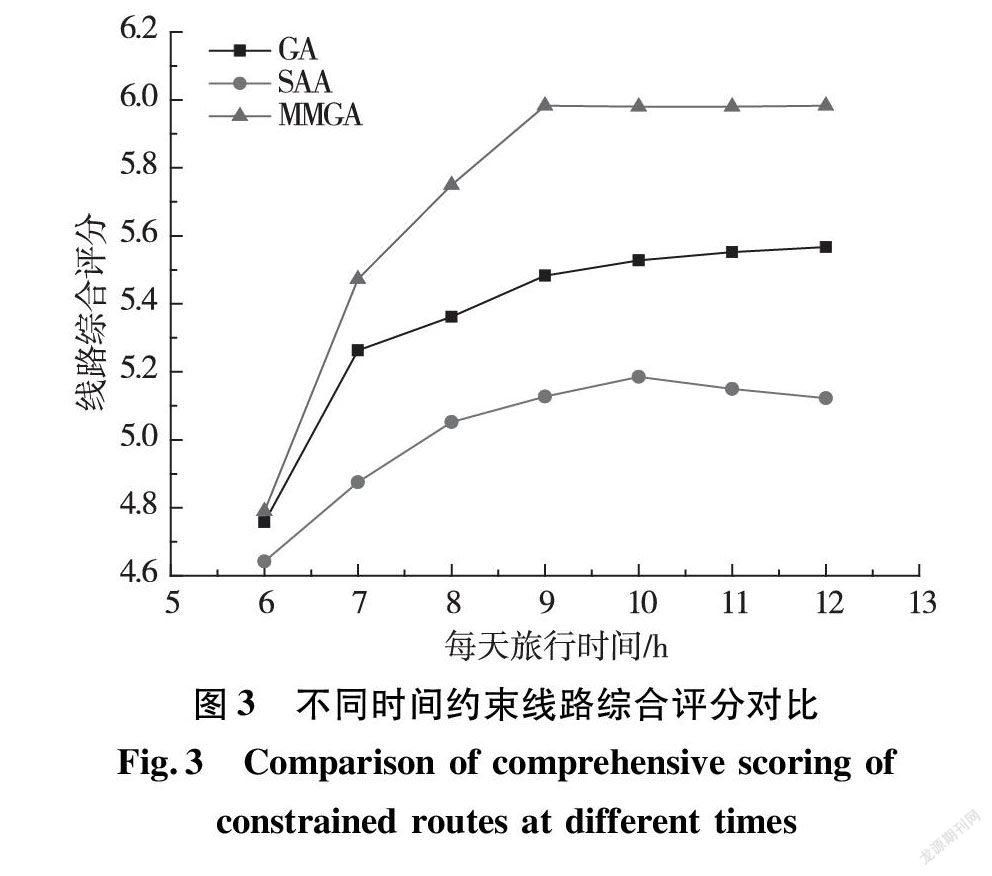
以旅行天数为2天为例,每天的旅行时间约束分别为6、7、8、9、10、11、12 h,得到不同时间约束下算法的对比,如图3所示。由图3可知,时间约束为9 h之前,3种算法的线路综合评分随着每天旅行时间的增加逐渐增加;时间约束为9 h之后,MMGA线路综合评分趋于平稳,SAA先增后降,GA则略有增长;与GA、SAA相比,MMGA线路综合评分最高,可以获取更高综合评分的线路。
2)相同时间约束不同旅行天数对比
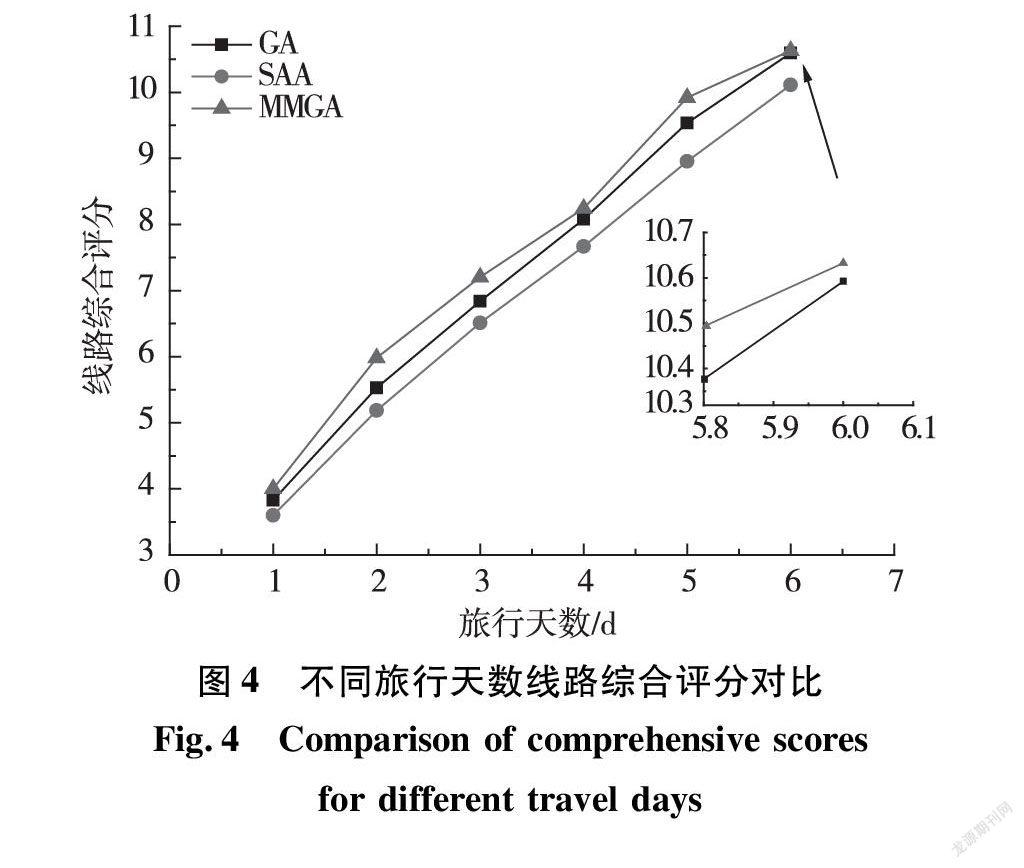
通常每天的旅行时间ts为8 h,依据景点的关闭时间,将每天的时间约束设置为10 h。以天数分别为1、2、3、4、5、6 d的旅游天数为例,进行6组实验,生成遵义会议的一日至六日游的旅游路线,如图4所示。由图4可知,不同旅行天数限制下线路综合评分的对比,MMGA可以获得更高的线路综合评分。
由于MMGA初始化种群产生方式的改进和多子代策略,算法中种群个体更为多样,后续参与遗传进化的种群个体有更高的适应度,使得算法可以快速获取优质可行解,有效避免了GA早收敛导致的局部最优问题,提升了算法的全局寻优能力。因此,MMGA在线路规划方面的结果要优于传统GA和SAA,能够推荐综合评分更高的線路,在满足景点热度的同时满足游客的文化需求,让游客可以充分游览景点,获得更好的旅游体验。但是,由于景点间的评分及文化特征差异较小(表2),导致不同算法推荐线路的综合评分差异不显著。
4 结论与展望
本文基于OPTW构建文化旅行线路规划模型,该模型综合考虑了游客的起始位置、文化偏好、旅行天数、景点开放时间等多种约束因素,并根据景点的文化特征综合评价景点,设置线路利益目标函数。为了有效求解上述模型,提出了MMGA,利用Jaccard提高初始种群质量,通过多变异算子保持算法进化过程种群多样性,提升了算法全局寻优能力。实验结果表明,MMGA相较于传统GA和SAA能够规划出更为合理的旅游线路。但改进的算法相较于原算法更为复杂,算法运行时间会增加,此外,线路规划没有考虑环境因素,例如游览当天的天气状况、交通状况等;因此,今后工作中可以考虑算法运行时间的优化及多种现实条件下的线路规划,使路线能更贴近实际。
参考文献:
[1]GAVALAS D, KONSTANTOPOULOS C, MASTAKAS K, et al. A survey on algorithmic approaches for solving tourist trip design problems[J]. Journal of Heuristics, 2014, 20(3): 291-328.
[2] GAVALAS D, KONSTANTOPOULOS C, MASTAKAS K, et al. Efficient metaheuristics for the mixed team orienteering problem with time windows[J]. Algorithms, 2016, 9(1):1-21.
[3] SYLEJMANI K, DORN J, MUSLIU N. Planning the trip itinerary for tourist groups[J]. Information Technology & Tourism, 2017, 17(3): 275-314.
[4] HUANG T, GONG Y J, ZHANG Y H, et al. Automatic planning of multiple itineraries: a niching genetic evolution approach[J]. IEEE Transactions on Intelligent Transportation Systems, 2020, 21(10): 4225-4240.
[5] 崔琪, 吴秀丽, 余建军. 变邻域改进遗传算法求解混合流水车间调度问题[J]. 计算机集成制造系统, 2017, 23(9): 1917-1927.
[6] ZHANG Y M, JIAO L J, YU Z J, et al. A tourism route-planning approach based on comprehensive attractiveness[J]. IEEE Access, 2020, 8: 39536-39547.
[7] MALIK S, KIM D. Optimal travel route recommendation mechanism based on neural networks and particle swarm optimization for efficient tourism using tourist vehicular data[J]. Sustainability, 2019, 11(12): 1-26.
[8] QIAN X H, ZHONG X P. Optimal individualized multimedia tourism route planning based on ant colony algorithms and large data hidden mining[J]. Multimedia Tools and Applications, 2019, 78(15): 22099-22108.
[9] LIN S W, YU V F. A simulated annealing heuristic for the team orienteering problem with time windows[J]. European Journal of Operational Research, 2012, 217(1): 94-107.
[10]UMBARKAR A J, JOSHI M S, HONG W C. Comparative study of diversity based parallel dual population genetic algorithm for unconstrained function optimisations[J]. International Journal of Bio-Inspired Computation, 2016, 8(4): 248-263.
[11]LI J C , LI L. A hybrid genetic algorithm based on information entropy and game theory[J]. IEEE Access, 2020, 8: 36602-36611.
[12]譚文安, 赵尧. 基于混沌遗传算法的Web服务组合[J]. 计算机集成制造系统, 2018, 24(7): 1822-1829.
[13]SUN N, LU Y. A self-adaptive genetic algorithm with improved mutation mode based on measurement of population diversity[J]. Neural Computing and Applications, 2018, 31(5): 1435-1443.
[14]WANG J, ERSOY O K, HE M Y, et al. Multi-offspring genetic algorithm and its application to the traveling salesman problem[J]. Applied Soft Computing, 2016, 43: 415-423.
[15]王福林, 付晓明, 朱会霞, 等. 基于两点交叉多子代遗传算法[J]. 东北农业大学学报, 2016, 47(3): 72-79.
[16]XIN J F, ZHONG J B, YANG F R, et al. An improved genetic algorithm for path-planning of unmanned surface vehicle[J]. Sensors, 2019, 19(11): 2640.
[17]付哲, 李軍. 高性能正则表达式匹配算法综述[J]. 计算机工程与应用, 2018, 54(20): 1-13.
[18]黄细嘉, 宋丽娟. 红色旅游资源构成要素与开发因素分析[J]. 南昌大学学报(人文社会科学版), 2013, 44(5): 53-59.
[19]ZHANG D H, YOU X M, LIU S, et al. Multi-colony ant colony optimization based on generalized jaccard similarity recommendation strategy[J]. IEEE Access, 2019, 7: 157303-157317.
[20]KATOCH S, CHAUHAN S S, KUMAR V. A review on genetic algorithm: past, present, and future[J]. Multimedia Tools and Applications, 2021, 80(5): 8091-8126.
[21]田竞, 王向东, 苏北, 等. 重走长征路: 红一方面军: 上[M]. 北京:华文出版社, 2016.
[22]田竞, 王向东, 苏北, 等. 重走长征路: 红一方面军: 下[M]. 北京:华文出版社, 2016.
[23]杜丽英. 重走长征路: 红二方面军[M]. 北京: 华文出版社, 2016.
[24]田晓虹, 田毅, 田竞, 等. 重走长征路: 红四方面军[M]. 北京: 华文出版社, 2016.
[25]田竞, 苏北. 重走长征路: 红二十五军[M]. 北京: 华文出版社, 2016.
[26]赵福超. 遵义会议前后六次政治局会议的内在历史联系[J]. 吉首大学学报(社会科学版), 2019, 40(增刊1): 145-148.
(责任编辑:周晓南)
Improved Genetic Algorithm to Solve the Problem of
Cultural Tourism Route Planning
ZHANG Ruijiao1, CHEN Chongcheng*1, HUAGN Zhengrui1, FANG Hui1,2
(1.Academy of Digital China(Fujian) Key Laboratory of Spatial Data Mining and Information Sharing of Ministry of Education, Fuzhou University, Fuzhou 350116, China; 2.Fujian Provincial Key Laborabory of Information Processing and Intelligent Control, Minjiang University, Fuzhou 350108, China)
Abstract:
Aiming at the nondeterministic polynomially problem(NP) characteristics of the tourist route planning problem and taking into account the diversity of cultural connotations of cultural tourist attractions, a genetic algorithm that can effectively maintain the diversity of the population is proposed to solve the tourist route planning problem. In order to solve the local optimization problem of the traditional genetic algorithms, the improved algorithm uses the Jaccard coefficient to generate the initial population and thus improves the population quality; After crossover operation, the multiple mutation operators are used to generate multiple offsprings, and the superior individuals of the offsprings and parents are retained, thus generating a new population and maintaining the diversity of the population in the evolutionary process. The experimental results show that the proposed algorithm can solve the tourism route planning problem more effectively.
Key words:
cultural tourism route planning; genetic algorithm; Jaccard coefficient; mutation operator; population diversity

