Selective Laser Melting under Variable Ambient Pressure:A Mesoscopic Model and Transport Phenomena

Renzhi Hu,Mnleln Luo,Anguo Hung,Jimin Wu,Qingsong Wei,Shifeng Wen,Liho Zhng,Yusheng Shi,Dmitry Trushnikov,V.Y.Belenkiy,I.Yu.Letygin,K.P.Krunkrn,Shengyong Png,*

a State Key Laboratory of Materials Processing and Die and Mould Technology,Huazhong University of Science and Technology,Wuhan 430074,China

b Department of Welding Production,Metrology,and Technology of Materials,Perm National Research Polytechnic University,Perm 614990,Russia

c Department of Mechanical Engineering,Indian Institute of Technology Bombay,Mumbai 400076,India

ABSTRACT Recent reports on the selective laser melting(SLM)process under a vacuum or low ambient pressure have shown fewer defects and better surface quality of the as-printed products.Although the physical process of SLM in a vacuum has been investigated by high-speed imaging,the underlying mechanisms governing the heat transfer and molten flow are still not well understood.Herein,we first developed a mesoscopic model of SLM under variable ambient pressure based on our recent laser-welding studies.We simulated the transport phenomena of SLM 316L stainless steel powders under atmospheric and 100 Pa ambient pressure.For typical process parameters(laser power:200 W;scanning speed:2 m·s-1;powder diameter:27μm),the average surface temperature of the cavity approached 2800 K under atmospheric pressure,while it came close to 2300 K under 100 Pa pressure.More vigorous fluid flow(average speed:4 m·s-1)was observed under 100 Pa ambient pressure,because the pressure difference between the evaporation-induced surface pressure and the ambient pressure was relatively larger and drives the flow under lower pressure.It was also shown that there are periodical ripple flows(period:14μs)affecting the surface roughness of the as-printed track.Moreover,the molten flow was shown to be laminar because the Reynolds number is less than 400 and is far below the critical value of turbulence;thus,the viscous dissipation is significant.It was demonstrated that under a vacuum or lower ambient pressure,the ripple flow can be dissipated more easily by the viscous effect because the trajectory length of the ripple is longer;thus,the surface quality of the tracks is improved.To summarize,our model elucidates the physical mechanisms of the interesting transport phenomena that have been observed in independent experimental studies of the SLM process under variable ambient pressure,which could be a powerful tool for optimizing the SLM process in the future.

Keywords:Selective laser melting Mesoscopic model Ambient pressure Transport phenomena

1.Introduction

Tremendous developments have occurred in the selective laser melting(SLM)of metals under atmospheric pressure over the past 20 years[1–5].Recently,SLM under a vacuum or lower ambient pressure environment was proposed as an alternative way to produce high-quality metallic products.The advantages of vacuum SLM are obvious,as compared with the traditional SLM process.Due to the extremely clean environment,the micro-oxidation defect is prevented in the vacuum SLM process[6].A smoother surface of the as-printed product(roughnessRa＜1μm)can be obtained during the SLM of titanium(Ti)under a vacuum environment[7].Although some phenomena have been partially understood viain situobservations[8–10],the complex molten pool behaviors that occur on very short time scales(10-6–10-3s)have been inadequately observed.At present,the thermodynamic and hydrodynamic behaviors of the molten pool during the SLM process under lower ambient pressure are not well understood.

Efficient modeling has exhibited great potential in making it possible to understand the physical behaviors that occur during the SLM process,because it greatly reduces the need for expensive and time-consuming trial-and-error experiments[11].Over the past decades,tremendous progress has been made in the mesoscopic modeling of SLM molten pool dynamics[12–21].Key physical factors such as laser irradiation,Marangoni force,surface tension,and recoil pressure have been taken into consideration in modeling.Körner et al.[12]employed the lattice Boltzmann method(LBM)to study the successive consolidation process in powder layers.Khairallah et al.[13]developed a mesoscopic model to investigate the formation mechanism of pores,spatter,and denudation using the Eulerian–Lagrangian method.However,existing models rarely consider the effects of variable ambient pressure.Furthermore,it should be noted that it is very timeconsuming to solve current mesoscopic models of SLM,because the printing process includes different spatial and temporal scales.To overcome this problem,efforts have been made to reduce the computational cost.Boley et al.[14]introduced highperformance computing technology into SLM modeling.Lee and Zhang[15]used non-uniform grids to simulate a typical SLM printing process on a personal computer,and showed that only 40 h are needed to resolve the detailed heat transfer,fluid flow,and free surface evolutions of a 0.6 mm-long track for typical process parameters.In short,the computational time is huge for the current mesoscopic models of the SLM process.Therefore,more efficient simulation methods need to be developed.

In this study,we first developed a mesoscopic phenomenal model of SLM under variable ambient pressure based on our recent similar studies on laser welding[22,23].Physical effects,such as surface tension,Marangoni force,recoil pressure,and ambient pressure are rigorously considered in this model by using an efficient octree-based adaptive mesh refinement(AMR)method.A surface pressure model is introduced to consider the influence of variable ambient pressure on the molten pool,according to our previous studies on laser welding[22,23].We used our numerical model to investigate the heat transfer and fluid flow behaviors of SLM 316L stainless steel powders under atmospheric pressure and low ambient pressure(100 Pa).We then analyzed our simulation results by comparing them with current available experimental data of the SLM of steel powders under variable ambient pressure.

2.Materials and methods

Fig.1 shows a schematic diagram of the SLM process.The mathematical model considers both the mesoscopic conduction and the convective heat transfer;phase transformations such as melting,solidification,and evaporation are also mathematically treated.The mesoscopic fluid flow of the molten pool is mainly considered to be influenced by ambient pressure,recoil pressure due to evaporation,surface tension,hydrostatic pressure,hydrodynamics pressure,and Marangoni shear stress.Transient free surface evolutions of the molten pool surface are also accounted for with the volume of fluid(VOF)method.The mixture model is used to treat the solid–liquid phase transformations during the SLM process[19–21].To make this complicated problem mathematically tractable,the powder of 316L stainless steel is assumed to be closely packed in a regular way.However,we noted that this simplification can be restrained because our model can input the real packing patterns of powders when the packing strategy is experimentally determined.

Fig.1.Schematic description of the computational domain.

The governing equations of mass continuity,momentum conservation,and energy conservation of the SLM powders are given as follows[22]:

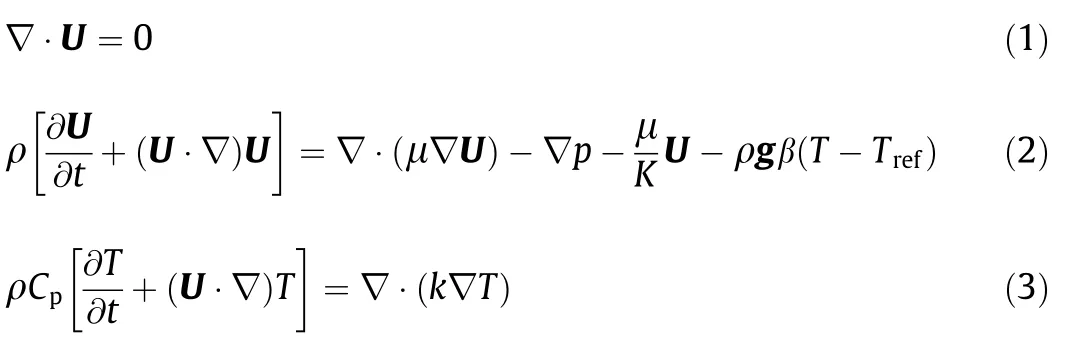
where ∇andtrespectively represent Hamiltonian operator and time.U,ρ,p,μ,g,T,Tref,β,Cp,andkrespectively represent the threedimensional(3D)velocity vector,density,pressure,viscosity,gravity vector,molten pool temperature,reference temperature,coefficient of thermal expansion,heat capacity,and thermal conductivity.Kis the Carman–Kozeny coefficient[24].The liquid/solid characteristics were accounted for with the field of liquid fractionfl.The liquid fraction is assumed to vary linearly with temperature[24]:

whereTlandTsrepresent the liquidus and solidus temperatures of the melt liquid,respectively.The interface between liquid and solid is determined when the liquid fraction is greater than 0 and less than 1.During the solidus/liquidus transformation process,a robust temperature compensation method[25]is used to treat the corresponding latent heat.

The VOF method is used to track the position and shape of a free surface.It solves a scalar transport equation for the volume fraction of metal in a cell(F)as follows[26]:

When the free surface is known,the absorbed energy densityqon the surface is calculated by a ray-tracing method[25].To reduce the computational cost,the multiple reflections of the rays are not considered[13],because this effect is negligible in the SLM process(note that the melting depth per track is usually small).The absorbed energy densityqon the metal surface can be expressed as follows[25,27]:

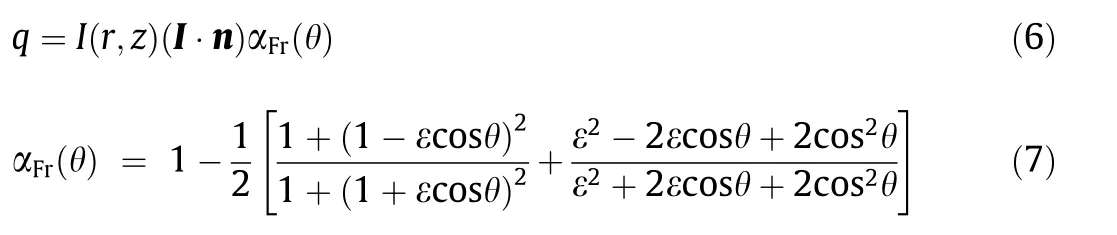
whereI(r,z)is the beam energy density distribution,randzrespectively represent the positions along the radius and theZaxis,I is the unit vector of the incident beams,n is the unit normal vector of the point on the metal surface,θ is the angle between the incident beam and the normal vector,αFris the Fresnel absorption coefficient,and ε is a coefficient related to the type of laser.I(r,z)is modeled as a Gaussian function[25]:

whereRis the effective beam radius andPis the laser power.

To treat the physical factors of the Marangoni force,recoil pressure,and surface tension action on the free surface,we adopt a balanced-force continuum surface force(CSF)algorithm to treat the boundary conditions[23,28].It is notable that this algorithm has been shown to be similar to the sharp interface method,which can also overcome the parasitic current problems in the simulation of capillary dominant fluid flows,such as fusion welding and 3D printing.The effect of these factors can be expressed as follows[23,28]:

where δsis a Dirac delta function.Fs,σ,κ,σT,and ∇‖respectively represent the normal stress of the interface,surface tension coefficient,interface curvature,thermal capillary force coefficient,and interface tangential gradient operator.To consider the influence of ambient pressure on the mesoscopic behaviors in the SLM process,we calculate the surface pressureps,which is related to the recoil pressure and the ambient pressure,in Eq.(8).We also adopt a surface pressure model to calculate the surface pressure[29].The surface pressure model is expressed as follows[29]:

wherepambis the ambient pressure,kBis the Boltzmann constant,βRis the condensation coefficient,Tvis the boiling point,P0is the atmospheric pressure,ΔHv=mLvrepresents the enthalpy of phase transition during vaporization(mis the mass per atom andLvis the latent heat of vaporization),Tfsis the surface temperature,andTLandTRare the temperatures of the two tangent points between the smooth curvepc(Tfs)with the ambient line and the recoil pressure curve.The derivation of the model is as follows.From previous studies[22,29],the classical formula of recoil pressure does not consider the effect of ambient pressure and is appropriate under the circumstances of a vacuum environment.To consider the effect of ambient pressure,three circumstances need to be respectively dealt with.First,when the temperature is quite high,the recoil pressure is larger than the ambient pressure by a considerable amount and the ambient pressure is negligible.The surface pressure is directly calculated by the classical formSecond,when the temperature is low enough,evaporation barely occurs,and the recoil pressure is therefore negligible.The surface pressure is considered to be equal to the ambient pressure.Third,to avoid discontinuity,a smooth curvepc(Tfs)is constructed to link the ambient line and the recoil pressure curve.More details can be found in Ref.[27].In the present work,a cubic polynomial is used to describe the smooth curve,which is expressed as follows:

where the coefficientsa,b,c,anddand the temperatures of the intersection points(TL,TR)are all shown in Table 1 for 316L stainless steel under 100 Pa and atmospheric ambient pressure.

After the coupled mathematical model is determined,we adopt an AMR method to solve the set of equations.Here,we use an octree-based AMR method in which a multiresolution algorithm is used to control the dynamic mesh refinement,following our previous studies[27,28].The key point of this method is to determine the difference between the original values of the physical fields and the reconstructed ones.In the present work,we set the mesh adaption to the free surface curvature and local temperature.Detailed strategies for AMR can be found in our previous study[27].

In the present work,to investigate the influence of ambient pressure on the transport phenomena,we simulated the SLM processes under atmospheric pressure and 100 Pa ambient pressure,respectively,using our model.We performed the process simulations in a 3D domain with the dimensions of 620μm(length),350μm(width),and 300μm(height),as shown in Fig.1.The domain includes a 54μm-thick layer of powder particles laid on a 200μm-thick substrate.The minimum size of the grid is set to 2.5μm to ensure accuracy.The powder particle diameter is 27μm.The particles are arranged simply and regularly.However,a better choice would be to use random distribution of the powder particles,which will be implemented in the near future.The laser power is 200 W,the scanning speed is 2 m·s-1,and the beam radius is about 27μm.To avoid reducing the accuracy of the simulation,the temperature-dependent thermal parameters of 316L stainless steel powder are used in the present work,according to Refs.[11,13],as shown in Table 2.The parameter values at any temperature can be obtained by interpolation or extrapolation.

Table 1 Parameters of the surface pressure model of 316L stainless steel under variable ambient pressure.

Table 2 Physical parameters used in the simulations[11,13].

3.Results and discussion

3.1.Temperature field and as-printed track morphology under variable ambient pressure

Figs.2(a)–(d)show the simulated evolutions of the temperature field and the free surface morphology during the SLM printing of 316L stainless steel powder under atmospheric pressure.When the laser scans from left to right,both the temperature field and the molten pool profiles gradually reach a quasi-steady state within approximately 100μs.In the quasi-steady state,it can be found that the temperature distribution is quite uneven.The maximum temperature exceeds the boiling point of steel(3083 K)in the region directly irradiated by the laser.The molten pool is exothermic and a large part of the temperature of the molten pool surface is around 2800 K.The width of the molten pool is about 73μm.The largest temperature gradient is estimated to be larger than 4.2×107K·m-1.(The difference between the highest temperature and the solidus temperature is about 1500 K,and the distance from the molten pool center to the edge is about 35μm.)Since the powders are assumed to be regularly packed in our model,the as-printed track is regular.Nevertheless,there are some small ripples(height:around 1μm;interval spacing:around 25μm)on the as-printed track surface because of the fluid dynamics of the molten pool.The ripple will be enhanced and may significantly influence the surface roughness of the as-printed products in a typical SLM process,because there are usually tens of thousands or even millions of tracks deposited in a layer-by-layer manner.Moreover,there are two distinct regions on the free surface of the molten pool(Fig.2(d)):The first is a cavity region in the front part,and the second is a relatively flat region located in the rear part.The diameter and depth of the cavity are around 50 and 20μm,respectively.Previous studies have shown that according to the laser power density and scanning speed,two regimes ofmelting modes(i.e.,the conduction mode and keyhole mode)will occur in an SLM process,such as laser welding[29].Since the temperature of the cavity region approaches the boiling point,intense evaporation will occur.Therefore,it can be concluded that in this process,keyhole-mode melting starts to occur,and the cavity region is produced by the displacement effect of the recoil pressure.Nevertheless,as the cavity is very shallow,the keyhole phenomenon is not obvious under the current process parameters.

Figs.2(e)–(h)show the simulated evolutions of the temperature field and the free surface morphology during the SLM printing of 316L stainless steel powder under 100 Pa ambient pressure.It can be seen that very similar physical behaviors occur under low ambient pressure,compared with those under atmospheric pressure.Nevertheless,several distinct characteristics are observable under lower ambient pressure.First,the temperature of the molten pool significantly decreases,as shown in Fig.2.The peak and average temperatures of the cavity region are only around 2600 and 2300 K,respectively,under 100 Pa ambient pressure,which are much lower than the corresponding temperatures(3100 and 2800 K)under atmospheric pressure.Furthermore,the heat transfer behavior is significantly different,which leads to different temperature distributions in the high-temperature regions of the molten pool under variable ambient pressure.In the cavity region of the molten pool,a higher temperature region occurs on the lateral sides of the molten pool in the cross-section direction,and a lower temperature region is in the center,as illustrated in Fig.2(h).However,under atmospheric pressure,the temperature is always high in the central part of the molten pool under the current process parameters.It is obvious that conduction heat transfer cannot be used to explain this phenomenon,because the energy distribution of the laser is Gaussian and the peak density is in the center.Therefore,only convective heat transfer can lead to such an unexpected phenomenon.A comparison of Figs.2(d)and(h)reveals that the convective heat transfer effect is enhanced in SLM under lower ambient pressure.In Section 3.2,we will show that there are more vigorous fluid flows in the lateral sides of the molten pool during SLM under lower ambient pressure than under atmospheric pressure.Moreover,the dimensions of the molten pool vary significantly when the ambient pressure changes from atmospheric pressure to 100 Pa.A much larger molten pool(width:80μm;depth:84μm)is found under lower ambient pressure than under atmospheric pressure(width:73μm;depth:28μm),as shown in Fig.3,and a smaller molten pool is observed under atmospheric pressure than under lower pressure,as illustrated in Fig.2(d)and Fig.2(h).Furthermore,it is interesting to note that under lower ambient pressure,the ripple of the molten pool is smaller and the as-printed track is smoother than under atmospheric pressure.

In order to verify the proposed model,we carried out simulations with randomly distributed powders.The process parameters remained the same.To randomly arrange the powders,the raindrop method was adopted[12].Compared with the uniform powder bed,an uneven deposit can easily be obtained,as shown in Fig.4(b).We compare the simulated molten pool profiles with independent literature results[11]for the SLM printing of the same material under atmospheric pressure in Fig.4 and Table 3.Both the melt width and depth are consistent with the independent experimental data.The maximum deviation is less than 6μm.Since the control data of the molten pool profile under lower or vacuum ambient pressure is not available,we compared the simulated varying trend of the physical behaviors with the literature reports.Our simulation results indicated that there are smaller ripples,and suggested that a smoother surface of the printed products would be obtained during SLM under lower ambient pressure.This result completely corresponds with all the previous experimental findings,which indicate better surface quality under a vacuum[6–10].Furthermore,our simulations of the temperature difference between the lower pressure case and the atmospheric are consistent with previous theoretical studies of laser welding[22,29,30].

Table 3 Comparison of the melt characteristics between the experimental results from Ref.[11]and the present simulation.

Fig.2.Evolutions of the temperature field and surface morphology.Under atmosphere pressure:(a)5μs;(b)80μs;(c)150μs;(d)220μs.Under 100 Pa pressure:(e)5μs;(f)80μs;(g)150μs;(h)220μs.

Fig.3.Calculated molten pool profiles at 220μs during SLM under variable ambient pressure.(a)Under atmospheric pressure;(b)under 100 Pa pressure.

In keyhole-mode laser welding,when the ambient pressure changes from a vacuum to atmospheric pressure,the weld width increases by some degree[22,29,30],which is different from the present simulation results of the SLM process.This difference can be explained as follows.In the present SLM process under atmospheric pressure,the melting mode can be largely considered to be the conduction mode,because the melting depth is very shallow,as shown in the present simulation and in previous independent literature reports[11,15,21].When the ambient pressure decreases to 100 Pa,the melting depth increases remarkably,and the melting mode starts to shift from the conduction mode to the keyhole mode,as shown in Fig.3.The convective heat transfer is enhanced because of the evaporation-induced recoil pressure;therefore,an increase of the melting width is observed based on the present predications.This phenomenon is consistent with the widely accepted phenomena of laser welding in which there are more vigorous fluid flows in the keyhole-mode welding process than in the conduction-mode process.

3.2.Fluid dynamics of molten pool under variable ambient pressure

Fig.5 shows the predicted evolutions of the flow field of the molten pool under atmospheric pressure.The velocity is plotted as arrows,and its magnitude is represented by the color of the arrow.There are two distinct flow regions(the cavity region and other parts)in the weld pool.In the cavity,the fluid is violent(up to 5 m·s-1),and mainly flows from the center to the peripheral regions of the cavity(Figs.5(b)–(e)).Since the temperature in the center of the cavity is higher than in other places and around the boiling point,this violent flow is induced by the Marangoni shear stress and recoil pressure.In the rear part of the molten pool,the fluid flows backward relative to the laser-scanning direction,and its magnitude is around 2 m·s-1in the quasi-steady state(Fig.5(d)).Moreover,the fluid flow in the weld pool exhibits periodic oscillations with a period of 14μs according to the simulated results.This flow mainly originates from the displacement effect of the recoil pressure on the front part of the cavity irradiated by a Gaussian laser beam.Its mechanism during keyhole-mode laser welding has already been well studied[22,25,29].The oscillation of the fluid flow produces ripples with a height of around 1μm on the as-printed tracks,under the current parameters.

Fig.6 shows the predicted fluid flow field of the molten pool under low ambient pressure at 150μs.This time ensures that the keyhole reaches a quasi-steady state.Similar flow patterns exist under low ambient pressure,as can be seen in comparison with Fig.5(e).This suggests that the mechanisms of the fluid mechanics of the molten pool under both ambient pressures are the same.Nevertheless,there are also distinct fluid flows in the molten pool,as shown in Fig.6.First,there are more violent flows in the lateral side of the molten pool under lower ambient pressure.The average magnitude of these flows is up to 4 m·s-1,as shown in Fig.6(b),compared with 2 m·s-1under atmospheric pressure.Second,keyhole-mode SLM also occurs in the lower ambient pressure environment;in this case,the printing process is more inclined to the keyhole mode because evaporation is easier under lower ambient pressure.The effect of the evaporation-induced recoil pressure will produce vigorous lateral sideway flows during laser interaction with materials.(Note that this mechanism was proposed nearly 20 years ago in laser welding[31].)Recently,the recoil pressure term was calculated as surface pressure by assuming that the evaporated atoms cannot flow freely until the temperature approaches the boiling point during the laser–material interaction[22,29,30].Under atmospheric pressure,the surface pressure only works when the material temperature is close to the boiling point(3086 K)[22].Under 100 Pa ambient pressure,the surface pressure starts to play an important role when the material temperature is much lower(around 2000 K for stainless steel),according to the Clapeyron–Clausius equation[22].This means that the pressure difference of the surface pressure and the ambient pressure—the major driving force of the fluid dynamics of the molten pool—is relatively larger under 100 Pa ambient pressure than under atmospheric pressure.This suggests that the boiling point will be significantly reduced under lower ambient pressure.It can easily be estimated that the boiling point will decrease by about 1000 K when the ambient pressure changes from atmospheric pressure to a vacuum for 316L stainless steel.Thus,intense evaporation occurs and a large surface pressure will be produced under 100 Pa ambient pressure when the material temperature is far from 3086 K.Therefore,in this case,the keyhole-mode SLM printing process is more likely to occur and more vigorous flows will exist in the lateral sides of the molten pool.

Fig.4.Validation of the model.(a)Randomly distributed powders;(b)predicted surface morphology at 250μs;(c)experimental results;(d)calculated molten pool profiles.(c)Reproduced from Ref.[11]with permission of Elsevier B.V.,©2014.

Fig.7 shows the predicted fluid flow inside the molten pool under different pressures.It can be seen that the flow patterns are similar,while the magnitudes are different.From the flow pattern,there is a vortex flow in the rear part of the molten pool.Part of the flow near the front surface of the molten pool is downward along the surface.The vortex flow results from the backward fluid flow,driven by the Marangoni shear stress and recoil pressure,encountering the solidified part.This kind of flow pattern is common in the laser-welding process[22].From the velocity magnitude,a larger local flow(up to 7 m·s-1)is found under 100 Pa pressure due to the aforementioned larger surface pressure effect.In addition,the magnitude of the backward flow decreases rapidly along the molten pool surface in the rear part under 100 Pa pressure.This indicates that the viscous dissipation is significant when the fluid flows along the surface of the deep cavity.From above,this demonstrates that the ambient pressure has a significant influence on the magnitude of the fluid flow.

3.3.Relationship between transport phenomena and printing quality improvement under lower ambient pressure

Previous independent experiments have shown that the asprinted quality of the SLM process can be improved(i.e.,with a smoother surface and fewer defects)when the SLM process is carried out in a vacuum or in a lower ambient pressure environment[6–10].Based on our mesoscopic mathematical model,we have directly reproduced the effect of lower ambient pressure to improve printing,as shown in Figs.3 and 8:The melting track width is larger,the track depth is deeper,and better surface roughness is simulated under lower ambient pressure.Below,we use fluid mechanics theory to explain these phenomena.

Fig.5.Predicted fluid flow under atmospheric pressure.The arrows denote the fluid velocity of the molten pool,and the arrow color indicates the velocity(vel)magnitude.(a)5μs;(b)15μs;(c)80μs;(d)150μs;(e)the local enlarged view of the fluid flow at 150μs and the free surface are transparently visualized to illustrate the 3D flow field.

Fig.6.Predicted velocity field under 100 Pa pressure at 150μs.(a)Top view;(b)local enlarged view of the fluid flow,in which the free surface is transparently visualized to capture the 3D fluid dynamics.

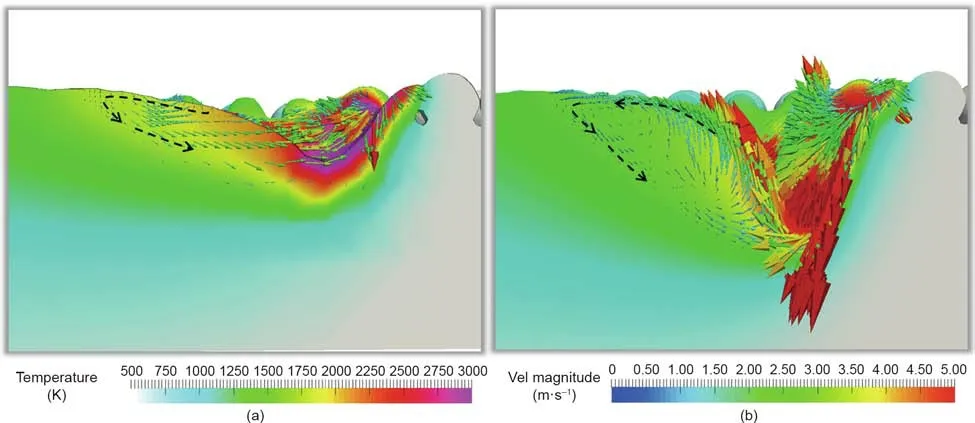
Fig.7.Predicted fluid flow inside the molten pool at 220μs.(a)Under atmospheric pressure;(b)under 100 Pa pressure.

Fig.8.Comparison of the simulated surface appearance under variable ambient pressure.(a)Atmospheric pressure;(b)100 Pa ambient pressure.

Our theoretical simulations showed that more vigorous fluid flows exist under lower ambient pressure(100 Pa)than under atmospheric pressure.It is known that the melting ability of powders during SLM is dominated by the heat transfer from the positions irradiated by the laser beam to other places.The Peclet number(Pe=UL/α,whereUis the average flow velocity(2 m·s-1under ambient pressure,4 m·s-1under 100 Pa pressure),Lis the characteristic length of fluid(the width of the molten pool,73μm under ambient pressure,80μm under 100 Pa pressure),and α is the thermal diffusivity(5×10-6m2·s-1)),which represents the degree of convective heat transfer(the dominant effect on the melting ability in the SLM process),is increased from 32 to 80.Therefore,the melting ability of the powders is remarkably enhanced under lower ambient pressure.Of course,lack of powder fusion,especially among adjacent paths,can be significantly improved.Moreover,due to enhancement of the convective heat transfer,both the melting width and depth are increased.Thus,the curvature of the molten pool is remarkably reduced under lower ambient pressure.This result also aligns with a previous experimental report,in lower ambient pressure prevent balling of powders in the SLM process[6].

Furthermore,our results showed that few ripples are produced under 100 Pa ambient pressure.The ripple flow,which originates from the front cavity wall,is transported from the bottom of the cavity surface to the rear part of the molten pool.The dimensionless Reynolds number of the molten flow(Re=ρUL/μ,ρ=7200 kg·m-3,U=2–4 m·s-1,L=7.3×10-5–8.0×10-5m,μ=5.9×10-3kg·m-2·s-1)can be estimated to be 170–390,which is far below the critical value of turbulent flow(Re＞2000)that indicates that the fluid flow is laminar in the SLM process.This means that the viscous effect plays a significant role in the fluid flow of the molten pool.Under 100 Pa ambient pressure,a deeper cavity is produced,which means that the trajectory length of the ripples(which originate from the front wall of the cavity)is longer.Of course,the ripple flow experiences more serious viscous dissipation under lower ambient pressure than under atmospheric pressure.Therefore,it can be understood that under a vacuum or lower ambient pressure,the ripple flow—a major cause of surface roughness—can be dissipated more easily by the viscous effect of the molten fluid,and the surface quality of the as-printed tracks can be remarkably improved,as shown in Fig.8.

4.Conclusions

A mesoscopic model of the SLM process under variable ambient pressure was first developed,and the transport phenomena under atmospheric pressure and under 100 Pa ambient pressure were then investigated.The main conclusions are as follows:

(1)The 3D heat transfer and fluid flow behaviors of the molten pool,as well as the as-printed morphology under variable ambient pressure,can be simulated by the model.The predicted molten pool dimensions are consistent with the independent literature results.

(2)The cavity produced by evaporation-induced recoil pressure forms more easily at the front part of the mesoscopic molten pool under lower ambient pressure.The average surface temperature of the cavity approaches 2800 K under atmospheric pressure,while it reaches 2300 K only under 100 Pa ambient pressure.This is primarily because the boiling point of stainless steel is much lower under low ambient pressure,and the material evaporates more easily in the lower pressure environment.

(3)Keyhole-mode SLM printing process is more likely to occur and more vigorous flows exist in the lateral sides of the molten pool under lower ambient pressure,because the difference between the evaporation-induced surface pressure and the ambient pressure—an important driving force of the melt flow—is relatively larger under 100 Pa ambient pressure than under atmospheric pressure.

(4)The relationship between transport phenomena and printing quality improvement under lower ambient pressure is revealed:Lack of powder fusion can be significantly improved,because the melting ability of the powders is remarkably enhanced by promoting convective heat transfer;and a smoother surface of the as-printed tracks can be obtained,because the ripple flow,which is a major cause of surface roughness,can be dissipated more easily by the viscous effect of the molten fluid under lower ambient pressure.

Acknowledgements

This research was supported by the National Science Fund for Excellent Young Scholars(52022033)and the National Key Research and Development Program of China(2017YFE0100100 and 2018YFB1105300),and was partially supported by the Government of Perm Krai(S-26/794)and the Russian Foundation for Basic Research(16-48-590208).

Compliance with ethics guidelines

Renzhi Hu,Manlelan Luo,Anguo Huang,Jiamin Wu,Qingsong Wei,Shifeng Wen,Lichao Zhang,Yusheng Shi,Dmitry Trushnikov,V.Ya.Belenkiy,I.Yu.Letyagin,K.P.Karunakaran,and Shengyong Pang declare that they have no conflict of interest or financial conflicts to disclose.