Atomic Force Microscopy Measurement in the Lignosulfonate/Inorganic Silica System:From Dispersion Mechanism Study to Product Design

Jingyu Wng,Yong Qin,*,Yijie Zhou,Dongjie Yng,Xueqing Qiu,b,*

a School of Chemistry and Chemical Engineering,South China University of Technology,Guangzhou 510641,China

b State Key Laboratory of Pulp and Paper Engineering,South China University of Technology,Guangzhou 510640,China

ABSTRACT Designing and preparing high-performance lignin-based dispersants are crucial steps in realizing the value-added utilization of lignin on an industrial scale.Such process depends heavily on an understanding of the dispersion mechanism of lignin-based dispersants.Here,atomic force microscopy(AFM)is employed to quantitatively investigate the dispersion mechanism of a lignosulfonate/silica(LS/SiO2)system under different pH conditions.The results show that the repulsive force between SiO2 particles in LS solution is stronger than it is in water,resulting in better dispersion stability.The Derjaguin–Landau–Verwey–Overbeek(DLVO)formula as well as the DLVO formula combined with steric repulsion is utilized for the fitting of the AFM force/distance(F/D)curves between the SiO2 probe and substrate in water and in LS solution.Based on these fitting results,electrostatic and steric repulsive forces are respectively calculated,yielding further evidence that LS provides strong steric repulsion between SiO2 particles.Further studies indicate that the adsorbance of LS on SiO2(Q),the normalized interaction constant(A),and the characteristic length(L)are the three critical factors affecting steric repulsion in the LS/SiO2 system.Based on the above conclusions,a novel quaternized grafted-sulfonation lignin(QAGSL)dispersant is designed and prepared.The QAGSL dispersant exhibits good dispersing performance for SiO2 and real cement particles.This work provides a fundamental and quantitative understanding of the dispersion mechanism in the LS/inorganic particle system and provides important guidance for the development of high-performance lignin-based dispersants.

Keywords:Lignin Silica Atomic force microscopy Dispersion mechanism Product design

1.Introduction

Due to the limited reserves of fossil fuels and the serious environment problems caused by their combustion,the utilization of biomass resources is attracting an increasing amount of attention.Lignin,the second most abundant component in plants,accounts for 15%–30% by weight of lignocellulose biomass[1].Industrially,(40–50)million tonnes of lignin are produced every year as byproducts from the pulp and papermaking industry and bioethanol fermentation[2].However,as-received lignin is mostly discarded or simply burned in order to generate basic thermal energy[3].Its hydrophobic aromatic skeleton and hydrophilic functional groups(e.g.,sulfonate,carboxyl,and hydroxyl groups)endow lignin and its derivatives with great potential for use in areas such as construction,agriculture,and energy[4–6].More specifically,a macromolecular dispersant is one of the most important lignin-based products used on an industrial scale.For example,lignin-based superplasticizers are widely used in the construction of buildings,bridges,and hydropower stations to effectively improve the performance of cement materials in terms of fluidity,hydration time,and durability[7–9].Lignin-based dispersants are usually characterized by their low cost,abundance,and sustainability,compared with other types of dispersants.However,high-performance polycarboxylate dispersant synthesized from petrochemicals has become increasingly competitive due to the low price of oil,especially in construction areas[10].In order to develop lignin-based dispersants with improved performance,it is imperative to gain a better fundamental understanding of the dispersion mechanism of lignin-based products.

Lignosulfonate(LS),a type of industrial lignin that is the byproduct of acidic sulfite pulping,is the most widely used lignin-based dispersant.Usually,LS is employed to disperse various inorganic oxide particles,such as cement,ceramic,and silica.In addition,LS and silica can be applied as precursors to produce advanced composite materials[11–15].For example,Klapiszewski et al.[13],Konował et al.[14],and Modrzejewska-Sikorska et al.[15]used LS as both reducing and stabilizing agents for gold/silver and selenium nanoparticles,which were further deposited on silica.Many efforts have been made to investigate the dispersion mechanism and to improve the dispersion performance of LS in inorganic oxide systems.Nevertheless,most of these analyses and results are based on indirect characterizations such as the rheological properties,zeta potential,and viscosity[16–18].Thus,direct and quantitative knowledge of the dispersion mechanism in LS/inorganic oxides systems is still missing yet necessary.

Atomic force microscopy(AFM)is widely employed to investigate molecular and interfacial forces in proteins,materials,and ligand–receptor systems;it enables researchers to obtain quantitative force mapping of physical,chemical,and biological interactions[19–25].Such quantitative understandings of interactions in different systems provide guidance for effectively designing high-performance materials[26–29].Zeng et al.[28]systematically measured the interactions between mussel foot proteins.Inspired by the results,they created engineered mussel adhesive proteins with very high dopamine content,which exhibited superior surface adhesion and water resistance[29].Qin et al.[30]investigated the interactions among different components in the cellulose hydrolysis process and found a strong attraction between lignin and cellulase.Their results showed that this attractive force was dominated by hydrophobic interaction.In order to avoid this binding and reduce the attraction between lignin and cellulase,a zwitterionic surfactant was designed and used in the cellulose hydrolysis process[31].This surfactant improved the enzymatic digestibility from 27.9%and 35.1%to 72.6%and 89.7%,respectively,in two different pretreatment systems.

In the current work,the interactions between SiO2particles and the substrate were quantitatively analyzed by AFM in both water and LS aqueous solution.The force/distance(F/D)curves were fitted using the Derjaguin–Landau–Verwey–Overbeek(DLVO)formula,as well as the DLVO combined with steric repulsion,and the electrostatic and steric repulsive forces were individually calculated.The characteristic parameters of the electrostatic and steric repulsive forces were calculated and compared in order to further demonstrate the dispersion mechanism of LS.Based on these results,an optimized LS-based dispersant—namely,quaternized grafted-sulfonation lignin(QAGSL)—was designed and prepared,and exhibited improved dispersion performance for SiO2and real cement particles.

2.Experimental methods

2.1.Materials

LS was produced from the sulfite pulping of poplar wood by Yanbian Shixian Bailu Papermaking Co.,Ltd.(China).It was separated into four fractions by an ultrafiltration apparatus(UF201,Saipu(Wuxi)Membrane Science and Technology Corp.,China).The fraction with a molecular weight(MW)of 10 000–50 000 was used in this work,and was composed of compact particles with no obvious pore structure(Figs.S1 and S2 in Appendix A).The morphology of the LS was observed using a highresolution scanning electron microscope(SEM;SU8220,Hitachi,Japan).The LS was milled carefully to obtain a fine powder;next,it was attached to conductive tape for SEM measurement.The specific surface area and the adsorption–desorption isotherm of the LS were measured using the Brunauer–Emmett–Teller(BET)method with an automated surface area and pore size analyzer(model TriStar II 3020,Micromeritics Instrument Corporation,USA).

SiO2standard particles with a diameter of 23μm were purchased from Suzhou NanoMicro Technology Co.,Ltd.(China).The SiO2substrate was purchased from Hefei Kejing Materials Technology Co.,Ltd.(China).Deionized water(resistivity ≥18 MΩ·cm-1)was obtained from a Millipore water purification system.The quaternization reagent 3-chloro-2-hydroxypropyl trimethyl ammonium chloride(CHPTAC)was purchased from Shanghai Macklin Biochemical Co.,Ltd.(China).Other reagents and solvents were purchased commercially as analytical grade products and were used as received without further purification.

2.2.Modification of the AFM probe and substrate

An AFM tipless probe(NP-O10,Bruker Inc.,Germany)with a nominal cantilever spring constant(0.12 N·m-1)was used in this experiment.Using a hot-melt adhesive,a SiO2particle was attached to the tipless AFM cantilever,as shown in Fig.1.

The LS was modified on the SiO2wafer to obtain LS-coated substrate.Prior to the experiments,the SiO2wafer was ultrasonically cleaned in 95%(volume percent)anhydrous ethanol solution.Next,the wafer was repeatedly rinsed with deionized water and dried using high-purity nitrogen.To obtain more–Si–OH groups and negative charges on the surface,the SiO2wafer was treated with plasma technology(30 min).Then,0.02 mmol·L-1of poly(dimethyl diallyl ammonium)chloride(PDAC)aqueous solution and 1 g·L-1of LS aqueous solution were successively coated onto the SiO2wafer by spin coating.The wafer was rinsed with deionized water to remove unstable LS.By means of the electrostatic force,positively charged PDAC was attached onto the negatively charged SiO2wafer surface.Moreover,the negatively charged LS was attached onto the PDAC polycation molecules;thus,the LScoated substrate was obtained.

2.3.AFM force measurement

Commercial atomic force microscope(XE-100,Park Systems,Republic of Korea)was used for all AFM force measurements.The force measurements were performed in a plastic dish filled with deionized water or 1 g·L-1LS aqueous solution at room temperature.Prior to the force measurements,the spring constant and deflection sensitivity of each cantilever were determined using the thermal method[21].In this work,the spring constant was(0.12±0.04)N·m-1and the deflection sensitivity was(47.8±2.3)V·μm-1.A limited force of 20.0 nN,a set point of 5.0 nN,a force distance of 1.0μm,and a vertical speed of 0.1μm·s-1were used for all AFM force measurements.The AFM force measurement included the approach and separation processes.In the approach process,the SiO2probe approached the SiO2substrate gradually.In the separation process,the probe and substrate were separated from each other.The AFM force measurement is sensitive,with a measured force in the nano-newton scale.Moreover,it was difficult to ensure that the substrate was the same in each location.Hence,a single measurement may contain a larger error.In order to eliminate the error as much as possible,the AFM force measurement was carried out 150 times at different locations of the substrate.There was a 300 s break between each of the 150 repeated measurements,which provided enough time for the rearrangement of the LS on the SiO2probe.

Fig.1.SEM image of a SiO2-coated AFM probe.The diameter of the SiO2 sphere is 23μm.

The adhesion force between the LS and SiO2was measured using a SiO2probe and an LS-coated substrate.The parameters and methods used were the same as those used in the measurement between the SiO2probe and SiO2substrate.

2.4.Fitting of the AFM F/D curve

The DLVO force between the tip and substrate for different geometries has been summarized by Israelachvili[32].In this work,a sphere–plate model was used for the interacting objects.The total DLVO force between the SiO2sphere probe and the SiO2substrate as a function of distance(D)is expressed as shown in Eq.(1):

whereDrepresents the distance between the SiO2probe and the substrate.In pure water,the zero point ofDwas defined as the contact point between the SiO2probe and the substrate.In the LS solution,due to the physical adsorption mode,the LS around the topmost point of the contact surface between the SiO2probe and the substrate was highly compressed and moved to the side.Therefore,the small area around the top-most point of the contact surface was almost bare,and the zero point ofDwas defined there.F(D)DLVOrepresents the DLVO force,F(D)VDWrepresents the van der Waals attraction force,andF(D)EDLrepresents the electrostatic doublelayer repulsive force.TheF(D)VDWcan be calculated as follows:

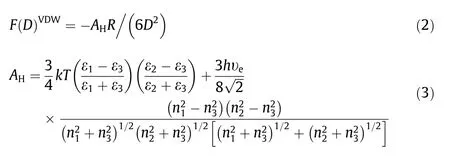
whereAHrepresents the Hamaker constant;Rrepresents the radius of the SiO2sphere(R=11.5μm);ε1,ε2,and ε3represent the static dielectric constants of the three media,respectively(i.e.,the SiO2probe,SiO2substrate,and water);n1,n2,andn3represent the refractive index of the three media at the wavelength of visible light,respectively;υerepresents the main electronic absorption frequency in the ultraviolet(UV)region,which is typically around 3×1015S–1;hrepresents the Planck constant,which is 6.63×10–34m2·kg·s-1;krepresents the Boltzmann constant,which is 1.38×10–23m2·kg·s-2·K-1;andTrepresents temperature.By substituting all the appropriate variables into Eq.(3),theAHbetween the SiO2probe and the SiO2substrate in water was estimated to be 6.3×10–21J.

TheF(D)EDLcan be calculated as follows:

where κ–1represents the Debye constant,Zrepresents the interaction constant of the electrostatic repulsive force,zrepresents the electrolyte valency,ψ0represents the surface potential,ε0represents the vacuum permittivity,and ε represents the relative permittivity of water.

The DLVO theory was employed to fit the experimentalF/Dcurves.According to Eqs.(1)–(5),the van der Waals force was negligible when the distance was large.Therefore,the DLVO force decayed nearly exponentially with distance.By applying exponential transformation,the transformed DLVO force decayed linearly with distance.Based on a linear fitting,the Debye constant(κ–1)and the interaction constant of the electrostatic repulsive force(Z)were calculated.The DLVO fitting curve was obtained by introducing the specific values of κ–1andZinto Eqs.(1)–(5).

For DLVO combined with steric repulsion fitting,theF/Dcurve at a large distance(D＞30 nm)was first fitted with the DLVO formula,because steric repulsion has no effect at such a distance.Next,the DLVO portion of the total force was subtracted,and the extracted data was used for the fitting of the steric repulsion.Finally,the DLVO fitting curve and the steric repulsion fitting curve were added to obtain the DLVO combined with the steric repulsion fitting curve.

2.5.Quartz crystal microbalance with dissipation monitoring measurement

A quartz crystal microbalance with dissipation monitoring(QCM-D;Q-Sense E1 instrument,Biolin Scientific,Sweden)was used to measure the adsorbance of the LS onto the SiO2substrate under different pH conditions.Deionized water(or an HCl solution at pH=3 and 5,or a NaOH solution at pH=9 and 11)was injected into the QCM-D flow module at a flow rate of 0.15 mL·min-1at 20°C.After baseline stabilization,the solution of 1 g·L–1LS aqueous solution was injected.The value of adsorbance can be calculated as follows:

wheremrepresents the adsorption capacity;Crepresents the mass sensitivity constant,which is 17.7 ng·cm-2·Hz-1;frepresents the resonance frequency;andnrepresents the overtone number.In this work,we choose the 3rd overtone number.

2.6.Dispersion stability measurement

The aqueous SiO2suspension was placed into cylindrical glass tubes and characterized by means of a Turbiscan LAB stability analyzer(Formulaction Co.,France).To scan the entire height(40 mm)of the aqueous SiO2suspension(20 mL)for 3 h,the two sensors of the optical analyzer received the transmitted and backscattered light.The stability analysis of the suspension was carried out by measuring the Turbiscan stability index(TSI)value.The TSI is a parameter that was specifically developed to rapidly compare and characterize the stability of various samples.Any destabilization phenomenon happening in a sample would be reflected by changes in the backscattering and/or transmission signal intensities.The sample with the highest intensity variation is the one that changed most significantly and is thus the least stable.The TSI calculation summed up the evolution of the transmission or backscattering light at all measured positions(p),based on the difference between one scan(i)and last time scan(i-1),over the total sample height(H):

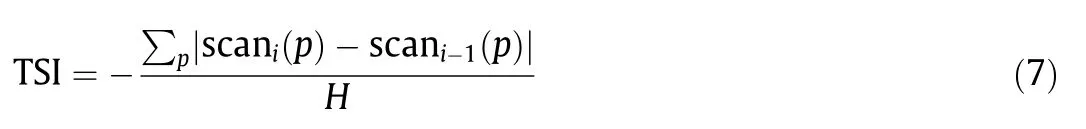
2.7.Rheometry

The viscosities of cement particles in three LS aqueous solutions were investigated at 25°C by means of a HAAKE MARS III rotational rheometer(Thermo Scientific,Germany).In this measurement,the mass ratio of water to cement was 0.35,and the mass ratio of LS to cement was 0.002.

2.8.Fluidity of the cement paste

The fluidity of the cement paste in three LS aqueous solutions was measured by pouring the cement into a plastic dish and recording the size of the cement cake.In this measurement,the mass ratio of water to cement was 0.35,and the mass ratio of LS to cement was 0.002.

2.9.Preparation and characterization of graft-sulfonated lignin and QAGSL

The graft-sulfonated lignin(GSL)was prepared using the following procedures.Sodium sulfite and acetone were first reacted at 45°C for 30 min.The lignin powders were then added into the reactor.The temperature was increased to 55°C and maintained for an additional 60 min.A 37%(weight percent)formaldehyde aqueous solution was then added into the reactor.During the feeding,the temperature of the solution increased automatically and was controlled to below 75°C.The details of this reaction can be found in our previous work[33].

The QAGSL was prepared by reacting the GSL with the quaternization reagent CHPTAC.A total of 70.0 g of GSL was dissolved in deionized water to prepare a 20%(weight percent)solution,and the pH was adjusted to 12 with NaOH.The temperature of the water bath was set to 85°C.When the temperature rose to 80°C,20.1 g of 65%(weight percent)CHPTAC solution was added into the flask at a rate of 3 mL·min-1.After 5 min,7.5 g of 20%(weight percent)NaOH solution was added as well,in order to keep the solution in an alkaline condition.The mixture was left to react for 4 h at 85°C.The solution was then purified by dialysis,using a dialysis bag to remove unreacted small molecules and inorganic salts.

The reaction scheme of GSL and QAGSL is shown in Fig.S3 in Appendix A.The Fourier-transform infrared(FTIR)spectra of LS,GSL,and QAGSL in the range of 4000–1000 cm-1were recorded by an FTIR spectrometer(Vector 33,Bruker,Germany).As shown in Fig.S4 in Appendix A,the signal at 1643 cm-1is the stretching vibration of C=O,and the signal at 1473 cm-1is the characteristic peak of the quaternary ammonium group.

The elemental compositions of LS,GSL,and QAGSL were measured using an elemental analyzer(vario EL III,Elementar,Germany).As shown in Table S1 in Appendix A,the increase of the sulfur element in GSL and QAGSL can be attributed to the additional introduction of the sulfonic acid group.The increase of the nitrogen element in QAGSL is the result of the introduction of the quaternary ammonium group.

3.Results and discussion

3.1.Repulsive force and dispersion stability of SiO2 in water and in LS solution

The scheme of the AFM force measurement process and a typicalF/Dcurve between the SiO2probe and the SiO2substrate in water is shown in Fig.2(a).The AFMF/Dcurve includes the approach and separation curves.In the approach process,the repulsive force increases gradually and reaches the maximum repulsive value just before hard-wall contact.This maximum value is recorded as the maximum repulsive force between the SiO2probe and the SiO2substrate.The maximum repulsive forces in water and those in LS aqueous solution were recorded from 150 repeated measurements at different locations of the substrate.As shown in the frequency distribution histograms(Fig.2(b)),the average value of the maximum repulsive force in water is(0.23±0.07)mN·m-1,while this value increases to(0.33±0.09)mN·m-1in LS aqueous solution.The specific values of the 150 repeated measurements are shown in Fig.S5 in Appendix A.There is no obvious increasing or decreasing trend over time,which demonstrates that the condition was stable throughout the AFM measurement process.The dispersion stability of the SiO2particles was compared in both water and LS aqueous solution.Here,a higher TSI value represents a lower dispersion stability.As shown in Fig.2(c),the TSI of the SiO2particles in the LS aqueous solution is smaller than that in water at pH=7.Moreover,the maximum repulsive forces and the TSI values of SiO2in water and in LS aqueous solution under different pH conditions are compared(Fig.2(d);see Figs.S6 and S7 in Appendix A for raw data).For all of the pH values considered in this study(pH=3–11),larger maximum repulsive forces and smaller TSI values are observed for the SiO2particles dispersed in LS solution than when they are dispersed in water.The results demonstrate that the larger repulsive force between SiO2in the LS solution contributes to the better stability and dispersibility of the SiO2particles.It is notable that such differences in the maximum repulsive forces and the TSI values in water and LS solution decrease with increasing pH,which indicates that LS improves the dispersion stability of SiO2more effectively under acidic conditions.Moreover,the fitting curve in Fig.2(e)shows that there is a positive correlation between the TSI values and the maximum repulsive forces,which suggests that the maximum repulsive force between SiO2particles plays a dominant role in its dispersion stability.

3.2.DLVO and DLVO combined with steric repulsion fitting in the LS/SiO2 system

In order to gain a better understanding of the dispersion mechanism of LS,the AFMF/Dcurves between SiO2in water and in LS solution were fitted using DLVO theory.The aggregation and dispersion behaviors of charged particles,including SiO2in water,can be explained by DLVO theory,which combines the effects of the van der Waals attraction and the electrostatic double-layer repulsion.The DLVO force can be expressed as shown in Eq.(1).The specific calculation formula of the DLVO force depends on the geometries of the interacting objects.In this work,a sphere–plate model was used for the interacting objects.The corresponding formula of this model has been described by Israelachvili[32].The van der Waals attraction force depends on the nature of the two interacting objects and does not significantly change with its surrounding conditions(Eqs.(2)and(3)).The electrostatic repulsive force can be calculated using Eq.(4).

DLVO theory was employed to fit the experimentalF/Dcurves between the SiO2probe and substrate in water and in LS solution.As shown in Fig.3(a),theF/Dcurve is consistent with DLVO theory in water.In contrast,theF/Dcurve is only consistent with DLVO theory at a large distance in the LS solution and differs from the DLVO fitting curve when the distance between the SiO2probe and substrate decreases to around 20 nm(Fig.3(b)).The DLVO force only contains electrostatic repulsion and the van der Waals force.However,steric repulsion also plays an important role in the presence of a polymeric dispersant such like LS.The steric repulsive force is induced when the adsorption layers of the polymeric dispersant overlap with each other.Although the origin of steric force is still controversial,most researchers consider that steric force comes from the entropy effect.In an LS/SiO2system,only the steric repulsion and electrostatic repulsion have an obvious effect when the distance between SiO2probe and substrate is relatively large,while other interactions such as repulsive hydration interaction and hydrogen bond interaction are short-range interactions.Hence,the difference between the experimentalF/Dcurve and the DLVO fitting curve in the LS/SiO2system can be mainly attributed to steric repulsion.

Fig.2.(a)Typical AFM F/D curve between the SiO2 sphere and SiO2 substrate;(b)histogram of the repulsive force between the SiO2 sphere and SiO2 substrate in water and LS aqueous solution at pH=7;(c)TSI of the SiO2 system in water and in LS aqueous solution at pH=7;(d)average maximum repulsive forces and TSI values(at 3 h)of the SiO2 system in water and in LS aqueous solution under different pH conditions;(e)correlation between the TSI values and maximum repulsive forces.

Fig.3.(a)AFM F/D curve and DLVO fitting curve between the SiO2 sphere and SiO2 substrate in water at pH=7;(b)AFM F/D curve,DLVO fitting curve,and DLVO combined with steric repulsion fitting curve between the SiO2 sphere and SiO2 substrate in LS aqueous solution at pH=7;(c)proportion of electrostatic repulsive force(Fe)and steric repulsive force(Fs)between the SiO2 sphere and substrate in LS aqueous solution at pH=7.

The electrostatic repulsive force and steric repulsive force are additive because there is no overlapping part between these two forces[34–36].Hence,to facilitate an individual analysis of the steric repulsion,the DLVO portion of the total force should be subtracted.As shown in Fig.S8 in Appendix A,the steric repulsive force decays exponentially with distance.The steric repulsive force can be influenced by many factors including the adsorption mode,adsorption density,solvent property,and so on[32].To the best of our knowledge,there is no unified formula to express steric force.In order to effectively compare the steric force supplied by LS under different pH conditions,all influencing factors were included in a factor defined asZs.Therefore,the steric repulsive force can be expressed as follows:

whereF(D)Srepresents the steric repulsive force,Zsrepresents the interaction constant of steric repulsion,andLrepresents the characteristic length of the steric repulsion.The total force,including both the DLVO part and the steric repulsion part,is expressed as follows:

As shown in Fig.3(b),theF/Dcurve measured in LS aqueous solution agrees with the DLVO combined with steric repulsion fitting curve.

Based on the above fitting results,the electrostatic and steric repulsive forces in an LS/SiO2system can be distinguished and analyzed separately.As shown in Fig.3(c),electrostatic repulsive force is a long-distance force,while the force range of steric repulsive force is relatively short.However,steric repulsive force increases faster than electrostatic repulsive force as the distance decreases.The proportions of the electrostatic and steric repulsive forces in the repulsive force are calculated and shown as dashed lines in Fig.3(c).The electrostatic repulsive force dominates the interaction between the SiO2probe and the SiO2substrate at a long distance in the LS solution,while the steric repulsive force dominates at a short distance.The fitting curves in water and LS solution under different pH conditions are further compared in Fig.S9 in Appendix A.The electrostatic repulsive forces between the SiO2probe and SiO2substrate increase with increasing pH in both the water and LS solution.However,the electrostatic force in LS is smaller than that in water,which demonstrates that although LS reduces the electrostatic repulsion between the SiO2probe and the substrate,it provides strong steric repulsion.The increase of the steric repulsive force is greater than the reduction of the electrostatic force,especially under low pH conditions.Hence,the repulsive force between the SiO2probe and substrate in LS aqueous solution is greater than that in water.

3.3.The characteristic parameters of electrostatic and steric repulsive forces in the LS/SiO2 system

The characteristic parameters of the electrostatic and steric repulsive forces were obtained from the fitting curves.In terms of electrostatic repulsion,a greater value of the Debye length(1/κ)represents a longer interacting distance,while a greater value of the interaction constant(Ze)represents a stronger interaction,which is due to the higher surface potential.Table S2 in Appendix A shows 1/κ andZeunder different pH conditions in both the water and LS solution.First,the theoretical values of the Debye length are compared with the experimental values to ensure the accuracy of the experimental results.The theoretical values in a 1:1 electrolyte solution,such as a solution of HCl or NaOH,can be calculated by Eq.(10):

whereMrepresents the molar concentration of the 1:1 electrolyte.The solution at pH=11 was prepared using NaOH,where 1 mmol·L-1Na+and OH–exist.The theoretical value of the Debye length in such a solution should be 9.6 nm,while the experimental value is 9.0 nm.The cation ionized from–Si–O–has similar properties to the electrolyte ion in the solution[37].Hence,this slight difference comes from the cations ionized from–Si–O–,which increase the electrolyte concentration in the solution.Upon comparing the difference between the theoretical and experimental Debye lengths,it was found that there were about 0.1 mmol·L-1of ionized cations.At pH 5–9,the ions in the water were mostly cations ionized from–Si–O–.If the concentration of the cations ionized from–Si–O–was still 0.1 mmol·L-1,the theoretical value of the Debye length should be 30.4 nm.But at a lower pH,the degree of ionization of–Si–O–decreases slightly.Hence,it is reasonable for the experimental values for the Debye length to be about 35 nm.At pH=3,the SiO2was almost nonionized.Therefore,the surface potential was too low to generate a measurable electrostatic double-layer repulsive force.All the experimental values of the Debye lengths in this work are consistent with the theoretical values.Moreover,theZebetween the SiO2particles in water increases as the pH changes from 3 to 11,because a more ionized–Si–O–increases the negative charges on the surface of the SiO2probe and SiO2substrate[38].In comparison,the 1/κ andZevalues in the LS solution are relatively smaller than those in water.For example,1/κ decreases from 35.7 nm in water to 25.0 nm in LS solution,andZedecreases from 1.07×10–11N in water to 4.0×10–12N in LS solution at pH=7.The ionized groups of the LS,including sulfonate,carboxyl,and phenolic hydroxyl,provide electrostatic repulsion when LS is adsorbed onto the surface of the SiO2.However,the counterions,such as the Na+ionized from LS,compress the double electric layer and weaken the electrostatic repulsion.Overall,LS is unfavorable for increasing the electrostatic repulsion between SiO2particles.

In terms of steric repulsion,the interaction constant(Zs)and the characteristic length(L)were considered.As shown in Eq.(8),Zsincludes many factors,such as the adsorbance of LS on SiO2(Q).The adsorption behavior of LS on SiO2under different pH conditions was investigated using a quartz crystal microbalance(QCM)and AFM.As shown in Fig.4(a),LS gradually adsorbs onto SiO2,and it takes 50–100 s for the adsorption to reach equilibrium.The adsorbance decreases from 3.89 to 0.59 mg·cm-2as the pH increases from 3 to 11.The adhesion forces between the LS and SiO2decrease from(0.65±0.14)mN·m-1at pH=3 to(0.20±0.09)mN·m-1at pH=11(Fig.4(b)).The interaction between LS and SiO2consists of both attractive forces,such as van der Waals forces and hydrogen bonding,and repulsive forces,such as electrostatic repulsive force.When the pH of the solution decreases,the degree of ionization of LS and SiO2decreases,thereby decreasing the electrostatic repulsive force;meanwhile,the attractive force does not change significantly.Therefore,the adhesion between LS and SiO2is enhanced,resulting in greater adsorbance and stronger steric repulsive force,which is confirmed by the steric repulsion constantZsdecreasing from 3.96 mN·m-1at pH=3 to 0.69 mN·m-1at pH=11,as shown in Table S3 in Appendix A.

Other effective parameters that affect the strength of the steric repulsive force in an LS aqueous solution are included in the normalized interaction constant(A),which is obtained by eliminating the influence ofQ,as shown in Eq.(11):

Fig.4.(a)Adsorbance of LS on the SiO2 substrate under different pH conditions;(b)adhesion force between LS and SiO2 under different pH conditions;(c)values of normalized interaction constant(A)and L under different pH conditions.

Fig.4(c)shows the values ofAandLunder different pH conditions.With an increase in the pH,Ldecreases from 6.7 nm(pH=3)to 3.1 nm(pH=11),whileAincreases from 1.5×10–3to 3.7×10–3N·m·kg-1.The size of LS in the solution plays a key role in determiningL.LS molecules tend to aggregate in water due to hydrogen bonding and π–π interaction.It has been demonstrated that LS aggregates more severely at higher pH,which leads to the formation of larger LS clusters[39].Hence,a largerLwas observed under acidic conditions.Ais influenced by several factors,such as the entropy effect,osmotic effect,and certain properties of the dispersant.In the LS/SiO2system,the intramolecular force of LS is one of the most essential factors affectingA.With increasing pH,the anionic groups of LS are gradually ionized,causing an increase of the intramolecular electrostatic repulsion.When one SiO2particle approaches another,the LS adsorption layers tend to compress and exhibit steric repulsion.The presence of more negative charges inside the LS at a high pH makes the LS more rigid and provides stronger steric repulsion,which is reflected by a largerA.

Based on the above results,Eq.(12)is proposed to calculate the contribution of LS to the maximum repulsive force between the SiO2particles:

where κ1and κ2represent the reciprocal of the Debye length of the electrostatic force between SiO2in water and in LS solution,respectively;andZe1andZe2represent the electrostatic repulsion constant between the SiO2in water and in LS solution,respectively.Because the electrostatic repulsion between the charged SiO2in water is strong enough,one strategy to obtain better lignin-based dispersants for SiO2is by enhancing the steric repulsion,which could be realized by increasing the values ofQ,A,andL.

3.4.Preparation of high-performance lignin-based dispersants

The LS-based dispersants GSL and QAGSL were designed as shown in Fig.5(a).Fig.S10 in Appendix A shows the maximum repulsive forces between the SiO2probe and the SiO2substrate in GSL and QAGSL aqueous solutions.The repulsive forces are larger in the GSL(0.53±0.06)mN·m-1and QAGSL(0.61±0.08)mN·m-1solutions than in the LS solution(0.33±0.09)mN·m-1at pH=7.The DLVO and DLVO combined with steric repulsion fitting curves in the GSL/SiO2and QAGSL/SiO2systems were obtained following the same formulas(Eqs.(1)–(5),(8),and(9)).As shown in Fig.S11 in Appendix A,the DLVO combined with steric repulsion fitting curves are consistent with the experimental data in both systems.The parameters of the steric repulsion were also calculated for these systems.As shown in Fig.5(b),Lincreases from 4.7 nm(LS)to 5.5 nm(GSL)and 5.4 nm(QAGSL),respectively,andAincreases from 3.0×10–3N·m·kg-1(LS)to 4.5×10–3N·m·kg-1(GSL)and 4.8×10–3N·m·kg-1(QAGSL)because the graftedsulfonated acetone formaldehyde polycondensate chains in the GSL and QAGSL enlarged their molecular size and enhanced the intramolecular repulsive force.Moreover,the cationic quaternary ammonium groups in QAGSL interact with SiO2by means of electrostatic attraction,which greatly increases the adsorbance of QAGSL on the surface of the SiO2from 1.77 mg·cm-2(LS)to 3.42 mg·cm-2(QAGSL)(Fig.S12 in Appendix A).The dispersion stabilities of the SiO2particles in the three solutions(LS,GSL,and QAGSL)are shown in Fig.5(c).As expected,due to its greater adsorbance and stronger repulsive force,QAGSL exhibits the best dispersing performance for SiO2particles.

Cement is one of the most typical silicate materials.Similar to SiO2,the silicon and oxygen elements in a cement particle form a tetrahedral silicon oxygen structure.The attractive interaction between cement particles in water is strong,which inhibits the flow of cement particles at a high concentration.Superplasticizer is used to decrease this interaction and increase the fluidity of cement.The viscosity reduction effect is one of the most important evaluation criterions for the performance of a superplasticizer.Three LS-based dispersants were used as cement superplasticizers,and their viscosity reduction effects on the cement were analyzed using a rheometer.As shown in Fig.5(d),the viscosities of the cement in the LS,GSL,and QAGSL aqueous solutions were 0.60,0.48,and 0.30 Pa·s,respectively,at a shear rate of 100 s-1.QAGSL exhibits a better viscosity reduction effect on cement particles in comparison with GSL and LS.Thus,the promoting effect of the QAGSL on the fluidity of the cement paste is also the best among the three LS-based dispersants(Fig.5(e)).

4.Conclusions

Fig.5.(a)Molecular structures of LS,GSL,and QAGSL;(b)values of Q,L,and A of LS,GSL,and QAGSL;(c)TSI values of the SiO2 system in LS,GSL,and QAGSL aqueous solutions at pH=7;(d)viscosities of cement particles in LS,GSL,and QAGSL aqueous solutions at pH=7;(e)promoting effects of LS,GSL,and QAGSL on the fluidity of cement paste.

In conclusion,AFM was used to study the dispersion mechanism of an LS/SiO2system under different pH conditions.Compared with SiO2in water,SiO2particles in LS solution presented larger repulsive forces and better dispersion stability.There was a positive correlation between dispersion stability and repulsive force.In order to obtain a better understanding of the dispersion mechanism of LS,the AFMF/Dcurves between the SiO2probe and the SiO2substrate in water and in LS solution were fitted.TheF/Dcurve was consistent with DLVO theory in water,whereas theF/Dcurve in LS solution needed to be fitted by the DLVO formula combined with steric repulsion.The fitted results demonstrated that the LS reduced the electrostatic repulsion between the SiO2particles while providing strong steric repulsion,especially under low pH conditions.The repulsive force between the SiO2particles was dominated by the electrostatic force at a long distance,while steric repulsion played a key role at a short distance.The adsorption capacity of the LS on SiO2(Q),the normalized interaction constant(A),and the characteristic length(L)were three critical parameters of the steric repulsion.These three parameters are enhanced with increasing pH value.The enhancement of these three parameters was favorable for improving the dispersing performance of the LS-based dispersants.A novel dispersant,QAGSL,which has higherQ,A,andLthan LS,was designed and prepared.QAGSL exhibited a better dispersing effect on SiO2and a stronger viscosity reduction effect on cement particles.

This work provides a fundamental and quantitative understanding of the LS dispersion mechanism.In addition,it gives important guidance for the development of high-performance lignin-based dispersants.The methods and results presented in this work could be extended to other lignin-based dispersant/inorganic material systems.Based on the quantitative measurement of the electrostatic and steric interaction factors in different systems,lignin could be modified more intentionally and accurately,so as to obtain high-performance lignin-based products effectively.

Acknowledgements

We gratefully acknowledge the financial support from the National Natural Science Foundation of China(21606089,21878113,and 21878114),the Guangdong Province Science and Technology Research Project of China(2017B090903003),and the Guangzhou Science and Technology Research Project of China(201704030126 and 201806010139).

Compliance with ethics guidelines

Jingyu Wang,Yong Qian,Yijie Zhou,Dongjie Yang,and Xueqing Qiu declare that they have no conflict of interest or financial conflicts to disclose.

Appendix A.Supplementary data

Supplementary data to this article can be found online at https://doi.org/10.1016/j.eng.2021.07.004.