问题出在哪里——对一个问题的深入探究

施刚良, 孟子君

(浙江大学附属中学丁兰校区，浙江 杭州 310021)

1 问题呈现

对于这个题目，文献[1]中作者呈现了两种解答：第一种(作者的解法)是利用正弦定理化边为角，转化为三角函数值域问题，从而得出正确答案；第二种(学生的解法)是通过余弦定理化角为边，利用基本不等式求解，结果与正确答案不符.文末，作者认为以上两种解法是解决三角函数的常用方法，学生的解法过程看似简单合理，但结果与标准答案相左，问题出在哪里？

2 问题的深入研究

在课堂教学后，笔者用此题作为学生的课后习题，批改过程中发现好多学生也采用第二种解法.学生做题往往不计后果，只要能做出来就好了.著名数学家波利亚曾说过：“没有任何一个题目是彻底完成了的，总还会有些事情可以做；在经过充分的研究和观察以后，我们可以将任何解题方法加以改进；而且无论如何，我们总可以深化对答案的理解.”文献[2]中几位老师通过探究给出了问题范围扩大的原因，但没有对问题做进一步探究，于是在笔者的脑海中产生了探个究竟的想法.

2.1 问题的另解

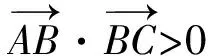
从而

3(b-c)2+(b+c)2=3.

(1)

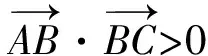
(2)

联立式(1)和式(2)，消去b-c，得

16(b+c)4-48(b+c)2+27<0，

即

从而

2.2 问题的一般化

从特殊到一般是研究数学的一般套路，这也是我们发现一些数学结论的基本思想方法.这类推理属于归纳推理，是逻辑推理的一种形式，也是我们教学过程中要着力培养的数学核心素养.通过类比，我们将题目一般化，得到：

评注当λ=1时，即为文献[1]中的问题.对于推广1，如果利用正弦定理化边为角，转化为三角函数值域问题求解，那么可能会遇到一定的麻烦，此时角A已不是特殊角了，有兴趣的读者可以探究一下.

我们发现上述解法极具启发性.下面给出具体的探究过程：

从而

(λ+2)(b-c)2-(λ-2)(b+c)2=3.

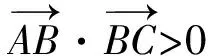
消去b-c，得

16(2-λ)(b+c)4-48(b+c)2+9(λ+2)<0.

(3)

解此不等式的难点是要考虑λ的范围，即缩小它的范围.事实上，根据余弦定理b2+c2-a2=2bccosA，可得

即

亦即

-2<λ<2.

因此，不等式(3)可变形为

[4(b+c)2-3][4(2-λ)(b+c)2-3(λ+2)]<0.

即

这显然不可能.

3)当λ=0时，显然也不可能.

通过上面的讨论，我们发现所得的一般性结论为：

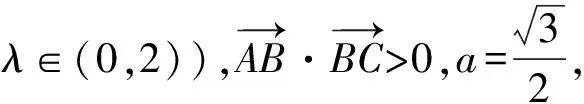
上面的讨论都是从代数运算的角度加以解决的.有学生提出：能否从几何的角度加以解决？通过观察b+c的结构特征，容易联想到椭圆的长轴长，于是想到能否从此角度加以突破？

图1

著名数学家波利亚又说过：“当你找到第一个蘑菇或做出第一个发现后，再四处看看，它们总是成群生长的.”此时，我们感觉还是意犹未尽，通过进一步探究得到了如下更加具有一般性的结论：

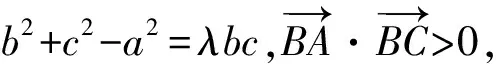
2)当-2<λ<0时，b+c>a>|b-c|.

通过变式探究，还可以得到如下类似的结论：

2)当-2<λ<0时，b+c>a>|b-c|.

评注结论1和结论2的证明方法与“另解”的思路相同，笔者在此不再叙述，留给有兴趣的读者探究.

3 结束语

正确的解答，可能是模仿；而错误的解答，却可能是创新，里面蕴藏着价值[3].要将错误为自己所用，必须将错误发生的来龙去脉搞清楚，这是一种经验的积累.

对错解的深入探究，能有效地提高一线教师的数学教学和研究水平.正所谓“百花齐放，百家争鸣”，有些问题通过大家的争辩、讨论，一开始可能百思不得其解，但通过持续地思考和探究，会使我们感到“醍醐灌顶”，体会到数学研究的乐趣，而这种乐趣是一般人感受不到的，这也使得我们更加深刻地理解数学.

对错解的深入探究，还能提高学生发现问题与解决问题的能力.如果我们能在具体的教学实践中，让学生对某个问题也来个“争鸣”，给学生开辟一个施展他们能力的平台，那么，学生通过思考、争论，最终解决问题时经历的感受也就“别有一番风味”.而且，这种感受与解决了几个习题是不一样的,可以极大地提高学生的逻辑推理和批判能力.