基于TA-ConvBiLSTM 的化工过程关键工艺参数预测

袁壮，凌逸群，杨哲，李传坤

（1中石化安全工程研究院有限公司，化学品安全控制国家重点实验室，山东 青岛 266071；2中国石油化工集团有限公司，北京 100728）

引 言

化工生产中，关键工艺参数的实时感知与精准预测对于监控运行状态和保障过程安全至关重要[1-2]，亦是实施先进控制及在线优化的基石[3]。针对反应过程的时滞性，预测模型帮助现场人员提前捕捉参量变化趋势，开展预知操作以维持装置平稳[4]，避免传感器故障导致的误判断、误响应。

随着智能仪表、传感网络及分散控制系统（distributed control system,DCS）的普及，化工产业迈入大数据时代[5]。海量数据被采集存储，如何挖掘其隐含价值成为新课题[3,6]。数据驱动从反映真实工况的历史数据入手，运用机器学习建立目标参数与关联变量的映射关系，无须繁复的理化机理便能实现灵活预测[7-8]：宋菁华等[9]将神经网络（neural network,NN）用于铁水汞含量预测；刘佳等[10]构建支持向量回归（support vector rregression, SVR）预测乙烯裂解炉收率；Geng 等[11]基于极限学习机（extreme learning machine, ELM）预测装置能效。然而，受限于单隐藏层网络结构，上述浅层算法的特征表达能力不足，复杂任务性能不佳[12-13]。

深度神经网络（deep neural network, DNN）是人工智能领域的革命性技术[3]，通过级联多个非线性处理层，它被赋予无穷的特征挖掘和函数拟合能力。首先，DNN 能直接处理类型多样的原始监测信号，逐层转换提取本质特征，不依赖人工经验[14]，在大数据时代价值巨大[1]；其次，化工过程机理复杂、模态多样，加之设备故障、原料变化等外部扰动，参数存在高度的相关性、耦合性和不确定性[15]，DNN强大的非线性映射能力更能表征此种复杂函数分布[7]；最后，化工生产具有动态时变性，不同时刻数据之间存在潜在关联[1]。现有方法多为假定样本相互独立的静态模型，缺少捕捉、解释和存储时序特征的能力[16]。DNN 中的长短时记忆网络（long short term memory，LSTM）凭借独有的记忆细胞和门结构可在学习当前动态行为的同时保证历史信息的持久留存[17]，探索间隔较远元素间的长期依赖性，避免长时间跨度造成信息丢失。因此，LSTM 广泛用于工艺参数和质量指标预测[2,4,13-14,16-18]，其衍生算法双向LSTM（bi-directional LSTM, BiLSTM）[12,19-20]更能同时分析数据在向前、向后两个时间方向上的未知关联，性能出众。

然而，BiLSTM 仍有若干不足：一方面，BiLSTM只擅长提取时序特征，对高维输入变量之间的空间关联欠缺深入考量[6]；另一方面，对目标变量影响更大的关键特征是沿时间轴非均匀分布的[18]，即BiLSTM 学习的时序特征对预测输出有不同影响。但回归层却对各时间步隐藏状态平等对待，忽略其重要性差异。输入序列较长时，容易主次不分导致重要信息被掩盖[16]。针对上述问题，本文利用DNN擅长组合不同结构以利用其各自优势完成复杂任务的特点，将卷积神经网络（convolutional neural networks, CNN）[21]、BiLSTM 和时间注意力（temporal attention,TA）机制[22]集成到统一框架内，提出深度预测模型TA-ConvBiLSTM。其中，CNN 能平缓数据波动，利用多核卷积运算分析高维输入变量间的空间关联；BiLSTM 从正反两个方向挖掘时序特征，相互约束以形成信息闭环，修正建模误差；CNN 和BiLSTM 构成混合模型，相互弥补以从过程数据中提取深度时空特征。进一步引入TA，根据输入和输出间的相关性强弱为时间步分配不同的权重，提升关键信息对输出的影响力，降低次要信息对预测的干扰。最后，实际工业案例验证了该方法的有效性和实用性。

1 理论背景

1.1 时间序列预测问题

参数预测的本质是时间序列回归。数据集D={(Xi,Yi)}，Yi∈Xi，Xi={xi1,xi2,…xid}，Yi=yi，i= 1,2,…,n。

Yi为目标变量，Xi为关联变量，n、d为数据长度和变量维度。时间序列回归是指从D中学习预测模型f，将当前时刻i及b步前的关联变量映射到p时刻后的目标空间[23]，即：

1.2 CNN

CNN 的核心是一系列可训练的卷积核，能从自身角度描述输入数据并对特定特征敏感：

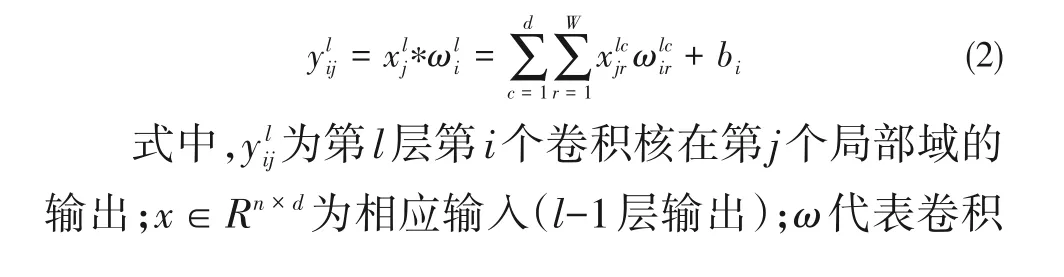
CNN通过池化层对卷积特征降维采样，只保留区域最大值或均值。但该操作可能中断序列连续性[24]，丢失时序信息，本文并未采用，后文将深入讨论。

1.3 BiLSTM

LSTM 的核心是记忆细胞和三种非线性门。LSTM 根据当前输入xt和上一时刻隐藏状态ht-1计算遗忘门ft、记忆门it和输出门ot，控制细胞的遗忘、记忆和输出，从而保留长期依赖性，遗忘次要信息，如图2所示。

图1 时滞样本集构造过程（b=3、p=1）Fig.1 The construction procedure of time-lagged samples with b=3 and p=1

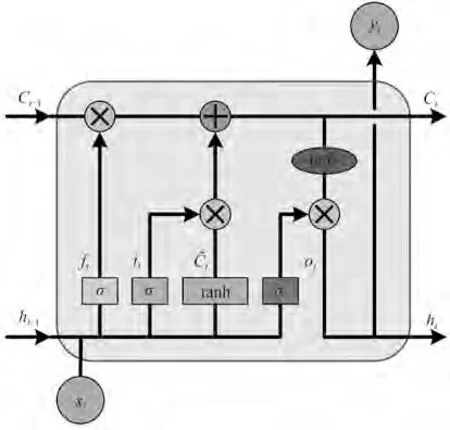
图2 LSTM网络结构Fig.2 Network structure of LSTM

遗忘门ft、记忆门it、临时记忆状态C͂t、记忆状态Ct、输出门ot和当前隐藏状态ht计算如下：

式中，σ和tanh 为sigmoid 及tanh 激活函数；Wf、Uf、Wi、Ui、Wc、Uc、Wo、Uo为各类门或状态的权值，bf、bi、bc、bo为偏置。

BiLSTM 由两个结构相同、方向相反的LSTM 组成，记t时刻正向LSTM 的输出为h→t，反向的为h←t，则BiLSTM的隐藏状态h↔t为：

式中，⊕为矩阵拼接操作。

1.4 TA机制

TA 可视为全连接神经网络。如图3 所示，当前时刻j的时滞样本{X1,X2,…,Xb}j经特征提取后，得到长度t的隐层输出{h1,h2,…,ht}j，输入TA 计算注意力值ei：

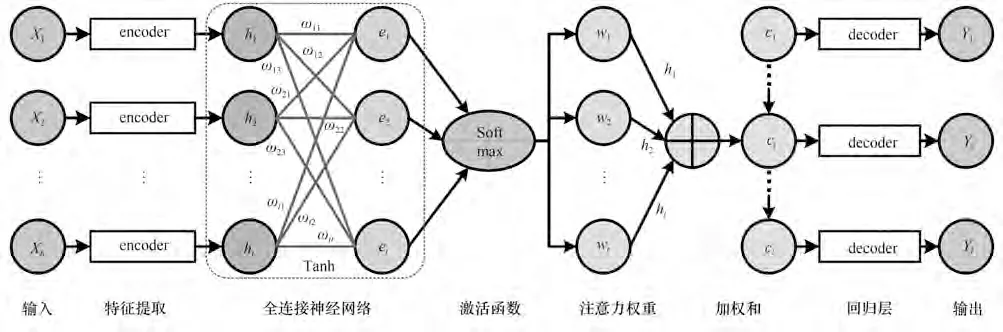
图3 TA机制结构Fig.3 Structure of the TA mechanism

式中，l=n-b-p+1 为时滞样本数量。最后，将cj代入回归层求解预测值Yj。

2 预测模型与流程

2.1 关联变量选择

工艺参数高维冗余，与目标变量的相关性也不尽相同，数据丰富但信息匮乏[6]。因此，需要筛选维度适当且重要独立的关联变量[25]。本文基于eXtreme gradient boosting（XGBoost）[26-28]算法选择关联变量，K次迭代输出预测值：

式中，下角标L 和R 分别代表左、右子树，选择Gain 最大的输入变量作为本次划分的节点。XGBoost 统计所有输入变量在分割时被选作叶子节点的次数，次数越多则该变量对预测模型的增益越大，重要度越高，可选取排序靠前的若干变量作为关联变量。

2.2 TA-ConvBiLSTM

XGBoost 选定k维关联变量，继续处理获得Ds={(Xs j,Y s j)}，Xs j∈Rb×k，1≤j≤l。将Ds输入TA-ConvBiLSTM并训练。

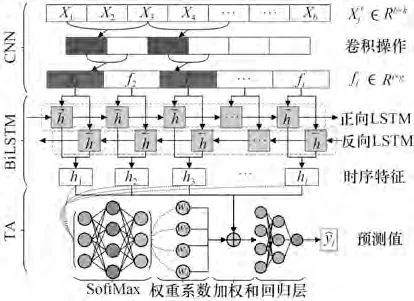
图4 TA-ConvBiLSTM 网络结构Fig.4 Network structure of the proposed TA-ConvBiLSTM

上述前向传播后，以均方误差（mean square error, MSE）作损失函数，开展反向传播（backpropagation,BP）：

式中，yj为第j个时滞样本的理想输出。以最小化MSE为目标更新模型，多次迭代完成训练。

2.3 预测流程

基于TA-ConvBiLSTM 的工艺参数预测流程如图5所示。

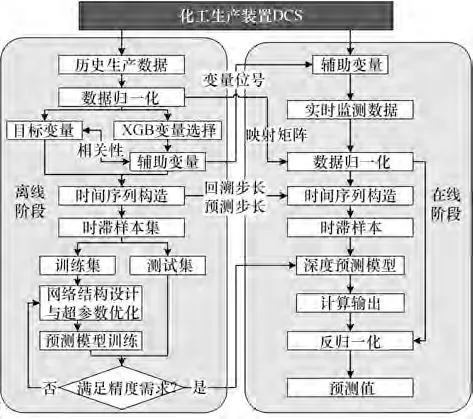
图5 基于TA-ConvBiLSTM 的参数预测流程Fig.5 Flowchart of parameters prediction based on TA-ConvBiLSTM

离线阶段：

（1）读取历史数据并归一化；

（2）确定目标变量，XGBoost 对所有工艺参数在预测中的重要度排序，选取前k组作为关联变量；

（3）确定回溯步长b和预测步长p，构造时滞样本集，并按比例分割为训练集和测试集；

（4）基于训练集训练TA-ConvBiLSTM，优化模型结构和参数；

（5）基于测试集验证TA-ConvBiLSTM 的预测精度是否满足要求。若是，则完成模型训练；若否，则重复步骤（4）。

在线阶段：

（1）读取k组关联变量的实时数据并归一化；

（2）根据b和p构造时间序列，获取时滞样本；

（3）将时滞样本输入训练好的TA-ConvBiLSTM中，计算输出；

（4）反归一化输出值，得到目标变量的预测值。

3 案例研究与分析

3.1 炉管温度预测

延迟焦化是一种原油二次加工技术，常用于劣质重油轻质化[29]，工艺流程如图6 所示。原料油经加热炉升温后通过四通阀进入焦炭塔中发生热裂化及缩合，产生油气进入分馏塔冷凝输出。其中，保持加热炉炉管各位置温度在适当范围内至关重要[30]：温度过高，炉管局部超温，油品在管内便裂解缩合导致结焦，能耗增加，持续超温更会损伤管壁，诱发泄漏着火等恶性事故；反之则炉出口温度降低，焦炭塔生焦反应深度不足，产物收率下降。生产中，若等到温度超限报警后再采取措施，结焦损伤已发生，且持续时间越长危害越大。因此，预测炉管温度并预知性地调整注汽量、燃料气压等参数，维持其在合理区间内波动，具有促进平稳运行和提升经济效益的双重作用。

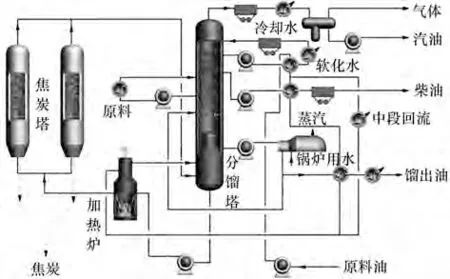
图6 延迟焦化工艺流程Fig.6 Flowchart of the delayed coking

3.2 应用案例

3.2.1 数据说明 从某延迟焦化DCS中读取2019年6～8 月的加热炉生产数据，选取炉管A 辐射段某温度测点y2jTI2012A 作目标变量，选取74维相关工艺参数（包括y2jTI2012A）作候选关联变量，部分变量信息见表1。为提高预测效率和时长，各参数每10 min 的测量均值作1 个样本，得到长度9000 的多维时间序列D∈R9000×74，并处理为时滞样本。沿时间流向，取前75%的样本作训练集，剩余作测试集，与随机划分相比该方式更符合工程实际。

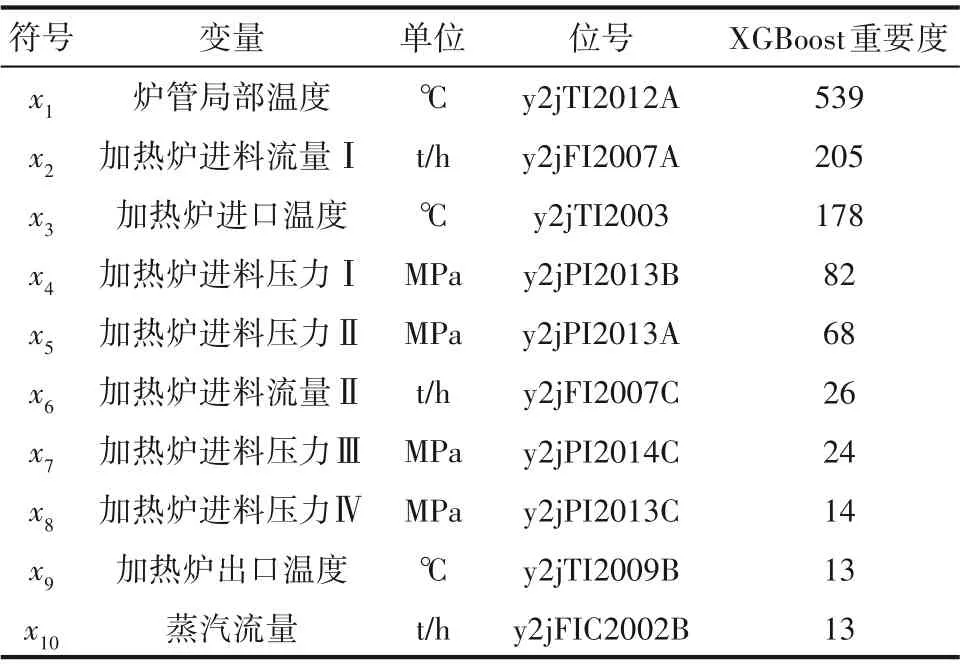
表1 部分候选关联变量及其特征重要度Table 1 Some candidate correlation variables and their characteristic importance

3.2.2 评价指标 选用平均绝对误差（mean absolute error, MAE）、均方根误差（root mean squared error,RMSE）和可决系数（coefficient of determination,R2）衡量预测性能：

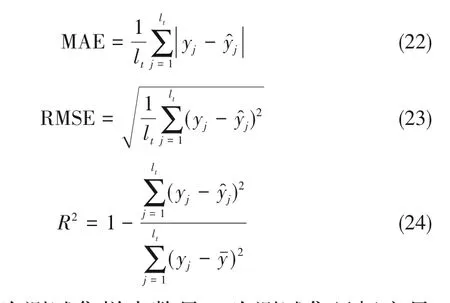
式中，lt为测试集样本数量；yˉ为测试集目标变量均值。MAE和RMSE反映预测值与真实值间的误差，越小越好，R2则反映二者的相似程度，越大越好。

3.3 预测效果分析

3.3.1 模型结构与参数设置 TA-ConvBiLSTM 的预测性能受网络结构、超参数及样本维度影响。

为讨论CNN 池化层对预测的影响，在结构5 第3 层后面插入一层池化层。采用最大值（maxpooling）和均值（mean-pooling）两种池化策略，不同池化尺寸下的预测精度如表3所示。由表3可知，池化层对预测有负面影响，且池化尺寸越大，降采样过程信息丢失越多，模型性能下降越大，不适用于本案例。

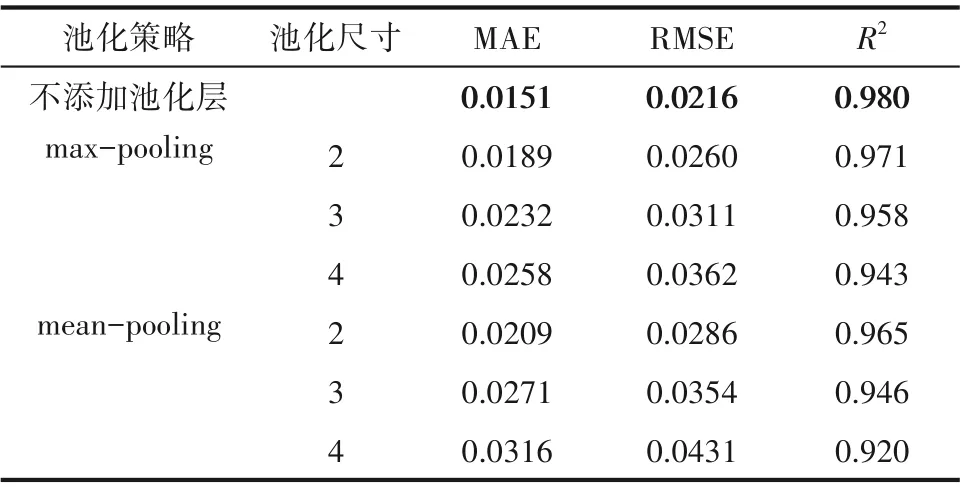
表3 不同池化尺寸下的模型预测性能Table 3 Model prediction accuracy under different pooling sizes

超参数方面，模型迭代500 epoch，early stopping patience 为100 epoch，Adam 算法自适应调整学习率，batch size根据表4设为128。

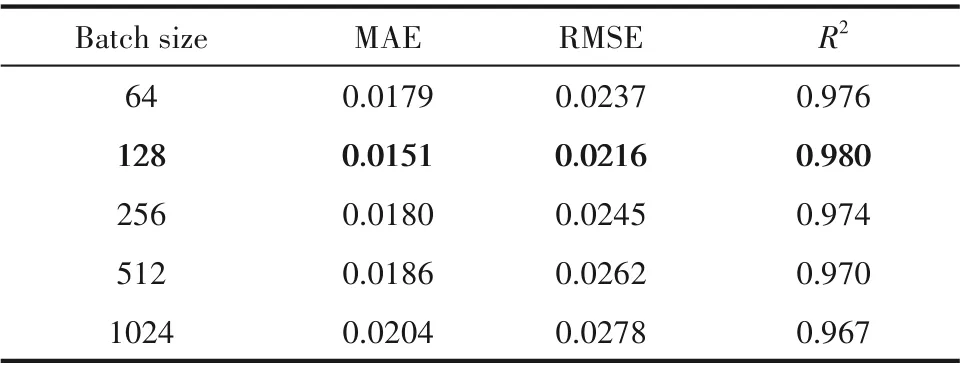
表4 不同batch size下的模型预测性能Table 4 Model prediction accuracy under different batch sizes

样本维度方面，XGBoost 对所有参数排序后，按照重要度从高到底依次选取前k={74,60,50,40,30,20,10,5}维参数作关联变量。由图7(a)可知，TAConvBiLSTM预测性能先随k减少而逐渐上升并在k=10时达到峰值。表明未经筛选的关联变量包含大量的冗余乃至无关信息，简单堆积只会降低运算效率而非提升预测效果。然而，k=5 时预测精度又大幅下降。表明剩余参数均与目标变量高度相关，继续缩减会缺失必要信息，难以全面衡量变化趋势。因此k=10较合适，选定的变量及重要度详见表1。

图7(b)分析了回溯步长b对预测的影响。理论上，序列越长蕴含的过程信息越多。但实际场景中，变量前后的潜在关联在多个时间步后便十分微弱，捕捉困难。而图7(b)中b=48时效果最佳，表明TA-ConvBiLSTM能有效处理长跨度序列，并保留其长期依赖性。

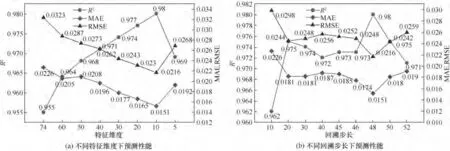
图7 输入维度对预测性能的影响Fig.7 The influence of input dimension on the prediction performance

表2 不同网络结构下的模型预测性能Table 2 Model prediction accuracy under different network structures

基于上述分析，本案例所采用的模型如表5(a)～(c)所示。

3.3.2 性能对比分析 除TA-ConvBiLSTM 外，还采用其他模型做对比分析：深度学习领域内，选取CNN 和LSTM 做基线模型，展现单一DNN 最大预测表现力；TA-ConvBiLSTM 框架内，各模块被拆解重组，证明其各自功能和集成作用，包括BiLSTM、ConvBiLSTM（CNN 与BiLSTM 级联）和TA-BiLSTM（BiLSTM 和TA 级联）。为增强说服力，上述方法也采用表5(a)～(c)的设置；浅层学习领域内，选取XGBoost、SVR 和BPNN 三种算法，限定b=1，其部分参数经遗传算法寻优后如表5(d)～(f)所示。

表5 网络结构与参数设置Table 5 Networks structure and parameters setting

直观比较各模型结果如图8所示。对于BPNN、SVR 和XGBoost，预测线与实测线之间始终存在较大偏差，预测线很难追踪实测线的快速波动和细微变化，表明浅层网络对时序数据缺乏动态表征能力。其相对预测误差分布在[-0.02,0.02]区间，且绝大部分位于零刻度线一侧，表明预测结果出现整体性漂移；CNN、LSTM、BiLSTM 及ConvBiLSTM 等深度模型大幅提升了预测线与实测线的贴合程度，能大致追踪真实温度的变化趋势。相对误差主要位于[-0.01,0.01]，特别是第100～750 样本点，因温度波动剧烈，误差幅值较大且相对集中；引入TA 后，TABiLSTM 和TA-ConvBiLSTM 的性能进一步提升，预测线和实测线几乎完全重合为一体，即使在曲线突变区域也有极高匹配度，相对误差也继续下降到[-0.005,0.005]，表明模型已充分掌握炉管温度的变化规律。TA-ConvBiLSTM 的误差控制更胜一筹，它分布在零线附近的误差“毛刺”更稀疏且幅值更小。

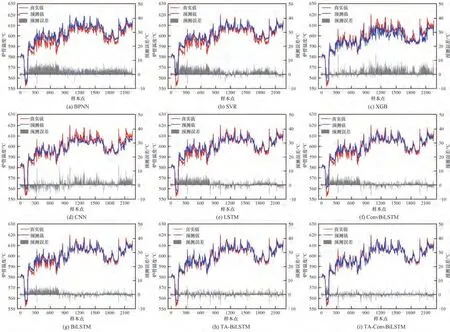
图8 各模型详细预测结果及误差Fig.8 Detailed prediction results and error of various testing models

表6对模型性能进行了量化排序。浅层模型性能最差，误差指标MAE、RMSE最高而准确度指标R2最低。因为浅层网络属于静态模型范畴，只能分析关联变量当前状态Xt和目标变量下一步状态Yt+1之间的关系（b=1），未考虑数据的时间性质；DNN 凭借强大的非线性拟合能力具有更优异表现。其中，尽管CNN 能分析连续时间序列，但本质仍为静态模型，擅长挖掘局部信息而非时序关联，结果最不理想。LSTM 则是专为序列处理而设计的动态模型，能够有效捕捉并存储长期依赖性，R2提升到0.947。BiLSTM 进一步从前后两个时间流向上挖掘引起温度波动的隐含因素，其优秀的动态建模能力使R2达到0.963。然而，ConvBiLSTM 的各项指标却弱于BiLSTM 单体模型，因为CNN 在每个时间步上都注入了丰富的细节信息，但BiLSTM 缺乏必要的区分机制，致使重要特征被遗失或掩盖；与之相比，TABiLSTM 和TA-ConvBiLSTM 则以各时间步的隐藏状态作参考，对其分配不同的权重以突出重要特征，弱化次要信息。两模型R2在引入TA 后分别提升了0.010 和0.024，证明了TA 的必要性。特别是TAConvBiLSTM，CNN 和TA 结合成为一种巧妙的时空注意力机制，不仅能在每个时间步上自主辨识与目标参数紧密联系的关联变量，还能横跨所有时间步自适应挖掘影响未来趋势的有用特征。因此，其MAE 和RMSE 分别为0.0151 和0.0216，远低于其他模型，R2更达到了最高的0.980。

表6 各模型预测性能对比Table 6 Comparison of prediction performance of various models

图9 以归一化的预测值和真实值为横纵坐标，绘制测试集的散点分布，并根据聚集情况讨论准确性。图中，对角线y=x表示预测值与真实值完全相同。因此，散点越逼近对角线精准度越高，异常风险越小。显然，TA-ConvBiLSTM 所属散点在对角线附近分布最为密集、距离最为接近，体现出预测模型对真实规律的高度还原。反观其他模型则要分散的多，预测结果不同程度地偏离了真实情况。

图9 各模型的预测散点图Fig.9 Predicted scatter plots of various models

图10 通过箱线图形象展示了各模型绝对误差的分布情况。箱线图能反映模型残差的极值、中值、均值、第25 和75 百分位，并直观呈现离群异常点。由图可知，TA-ConvBiLSTM 的误差中值及均值非常接近零刻度线，具有最高的平均预测准确度，其他算法则不同程度地偏离。 此外，TAConvBiLSTM 的箱体宽度也远小于各对比算法，展现出更窄的误差范围和更佳的预测稳定性。但是，TA-ConvBiLSTM 上下截断点间的内限区域（1.5IQR）也随之缩小，造成其异常点较多。

图10 各模型绝对预测误差的箱线图Fig.10 The box-plot diagram of absolute prediction error of various models

4 结 论

本文提出了TA-ConvBiLSTM 模型，用于表征复杂化工过程的高维相关性和动态时序性，弥补传统数据驱动方法在特征提取和参数预测方面的不足。加热炉炉管温度的预测实验证明了该方法的有效性和适用性，其R2高达0.980，MAE 和RMSE 也分别降至0.0151 和0.0216，明显优于其他方法。本文的主要创新点和贡献总结如下。

（1）基于DNN 擅长自由组合以解决复杂任务的优势，将CNN 和BiLSTM 集成为统一的深度网络，使之能够兼顾空间关联提取和时序特征挖掘。

（2）将TA 机制进一步融入上述预测框架，分析深度特征与目标输出间的相关性并增加关键信息的注意力权重，避免其因为序列延长而被淹没，提高建模的准确性和鲁棒性。

后续研究将对模型性能做进一步优化，解决现有分析所暴露出的不足。例如，TA-ConvBiLSTM 在箱线图中虽然具有最高的整体预测精度，但其异常点数量也要多于其他算法，仍需持续改进。