过冷流动沸腾中气泡浮升直径的实验及理论研究

周培，张秀平，唐景春，杨磊，叶斌，黄荣华

（1 合肥工业大学汽车与交通工程学院，安徽合肥 230009； 2 压缩机技术国家重点实验室（压缩机技术安徽省实验室），安徽合肥 230031； 3 华中科技大学能源与动力工程学院，湖北 武汉 430074）

引 言

随着发动机往高紧凑、高功率方向发展，发动机的热负荷越来越高，为保证发动机正常工作，亟需更加高效的冷却系统[1-2]。由于过冷流动沸腾冷却具有换热效率高、冷却介质流量小以及冷却温度均匀等优点，基于过冷流动沸腾的高温冷却系统受到越来越多的关注。但是，目前过冷流动沸腾的相关传热机理仍不完善，这导致高温冷却系统在发动机中的应用仍有一定的限制[3]。Mohanty 等[4]指出过冷流动沸腾传热效果直接与气泡行为相关，气泡行为是建立过冷流动沸腾传热机理的关键。Basu 等[5]和Gliman 等[6]的研究表明，气泡脱离直径和气泡浮升直径会影响到瞬态激冷传热和滑移传热的面积占比及蒸发传热的大小，在壁面传热机理模型中尤为重要。因此，十分有必要对发动机冷却水套内过冷流动沸腾的气泡特征直径进行研究。

常见的气泡特征直径描述有三种：气泡脱离直径Dd、气泡最大直径Dm和气泡浮升直径Dl[3,7]。气泡特征直径的建模方法也有三种：经验公式、能量平衡方法和力平衡方法。其中经验公式法是基于实验数据，将与气泡特征直径相关的影响因素进行数学公式拟合得到。Tolubinsky 等[8]根据高压环境下的水沸腾实验数据进行拟合得到气泡浮升直径公式，该模型与过热度相关，形式简单，在商业软件中得到了广泛的应用。Prodanovic 等[7]根据实验数据分别对气泡浮升直径、气泡最大直径与无量纲参数（沸腾数、Jacob 数和无量纲过冷度）进行数学拟合。Basu 等[5]引入了壁面接触角对特征尺寸的影响，基于自己的实验数据，分别对气泡脱离直径和气泡浮升直径进行建模，从实验数据与模型可以看出，接触角对气泡特征尺寸影响很大。Situ 等[9]基于力平衡模型推导出一个无量纲形式的气泡浮升直径模型，该模型是Jacob 数和Prandtl 数的函数，该模型的预测值与实验数据吻合较好。Brooks 等[10]和Du 等[11]利用前人的数据对气泡脱离直径进行建模，得到了一个适用范围比较宽的气泡脱离直径模型。Du 等[11]研究发现水平通道的气泡在脱离时刻的受力不同于垂直通道内的气泡受力，并基于前人的大量实验数据建立了水平通道和垂直通道的气泡脱离直径经验模型。气泡特征直径的经验模型结构简单，方便获得气泡特征数据，但是这些模型通常应用范围比较窄，仅和学者自己的实验数据吻合，很难广泛应用于其他的领域中。

气泡特征直径的另一种获得方法是能量平衡法，Han 等[12]采用能量平衡过程获得了池沸腾内的气泡浮升直径模型。Ünal[13]针对过冷沸腾下的气泡特征尺寸进行研究，采用能量平衡方法，引入气泡微液层[14]、过热层蒸发和冷凝从而得到气泡最大直径模型，该模型工况范围很宽广：系统压力1～177 bar（1 bar=105Pa），壁面热流470～10640 kW/m2，速度0.08～9.15 m/s 和过冷度3～86 K。Morel 等[15]对该模型进行修正，使其在饱和沸腾下仍继续适用。Dong 等[16]采用了与Ünal[13]类似的能量平衡方法，建立了过冷流动沸腾的最大气泡直径模型，该模型与实验数据吻合较好。

第三种方法是采用力平衡方法来获取气泡特征尺寸，通过力平衡方法可以获得气泡脱离直径和气泡浮升直径。该方法是通过气泡在加热面平行方向和垂直方向的力平衡的破坏进行判断，如果是加热面平行方向的力平衡先被破坏则气泡会沿着壁面滑移；如果是垂直加热面方向的力平衡先被破坏则气泡会垂直浮升[17-18]。早期研究主要针对池沸腾内的气泡浮升直径进行力平衡分析，得到形式比较简单的气泡浮升直径模型。Klausner 等[17-18]开发了一个考虑更全面的力平衡模型来预测气泡脱离直径和浮升直径，该模型与实验数据吻合较好。之后，有很多学者开始在该力平衡模型的基础上进行改进以提高预测精度，例如提出提高气泡生长模型预测精度、提高气泡壁面接触直径等子模型等[18-25]。Gao 等[26]采用自己开发的气泡生长模型对该力平衡模型进行修正，使得该力平衡模型在亚大气压下仍有很高的预测准确度。Wang 等[27]建立一种适用性更广的力平衡模型，但模型结构复杂，计算难度较大。从现有的研究可得出，力模型发展仍不完善，预测精度较低，需要进一步完善。

发动机缸盖多是水平布置，缸盖内的沸腾主要发生在火力面一侧，发动机水套内沸腾属于水平方向的过冷流动沸腾[28-29]，而过冷沸腾的流动方向会影响气泡特征直径[11,30]。目前，关于过冷流动沸腾气泡特征直径的研究多是竖直方向的流动，而针对水平方向且高流速下气泡特征直径的研究较少[3]。气泡特征直径的大多数研究是针对气泡脱离直径，而针对气泡浮升直径的研究较少，尤其关于发动机水套内过冷流动沸腾状态下气泡浮升直径的研究鲜有报道。因此，亟需开展高流速下水平流动过冷沸腾的气泡浮升直径研究。缸盖内沸腾气泡的可视化方法有缸盖局部开窗法[31]和内窥镜法[32]，这两种方法成像效果均不理想，导致气泡数据的提取难度大。发动机工况多变、结构复杂，缸盖内部的局部流动和温度参数测量难度大，这加大了气泡行为特性定量分析的难度。为解决以上难题，本文设计出与发动机水套沸腾区域水动力相似(Reynolds 数60000～120000)的矩形实验段，并设计了一个封闭循环的可视化实验系统。基于该实验系统，对高流速下水平方向过冷流动沸腾的气泡浮升直径进行研究，并建立气泡浮升直径的力平衡模型，为发动机内过冷流动沸腾的预测提供数据支撑及理论依据。

1 实验装置及误差分析

1.1 实验装置

针对发动机缸盖内的沸腾特性，搭建过冷流动沸腾实验装置，原理如图1所示。该实验系统包括：实验段、管路系统、压力控制系统、水温控制系统、变频驱动系统、数据采集系统以及其他子系统。其中数据采集系统由电磁流量计、压力传感器、T 形热电偶、NI 温度采集卡、高速摄像机、LED 灯及计算机组成，该系统可采集进出口流体温度、系统压力、流量以及气泡图像信息等。

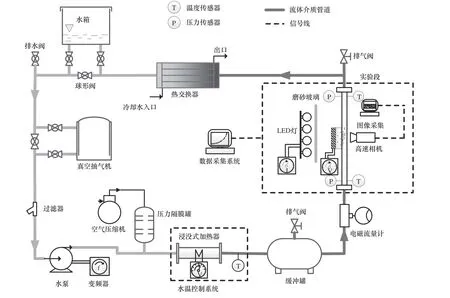
图1 过冷流动沸腾可视化实验装置示意图Fig.1 Schematic diagram of subcooled flow boiling experimental device

实验段的详细示意图如图2所示，实验段通道尺寸为400 mm×26 mm×16 mm(长×宽×高)。铝材加热块通过10个加热棒加热，最大加热功率3.5 kW，加热功率可由两相电压调压器进行调节，加热块的加热面尺寸为100 mm×14 mm。热电偶(直径0.5 mm)分成上下两排安装于加热块内部，加热面的加热功率和壁面温度通过傅里叶导热定律求解。为防止加热块的热流往周围壁面热传递，加热块周围的缝隙均填充珍珠粉。为防止漏水，在靠近加热面顶端位置的缝隙中填充有机硅密封胶。为保证流体介质在实验段处于充分发展状态，实验段的上游连接长1.0 m的延长段，实验段的下游连接长0.6 m的延长段。

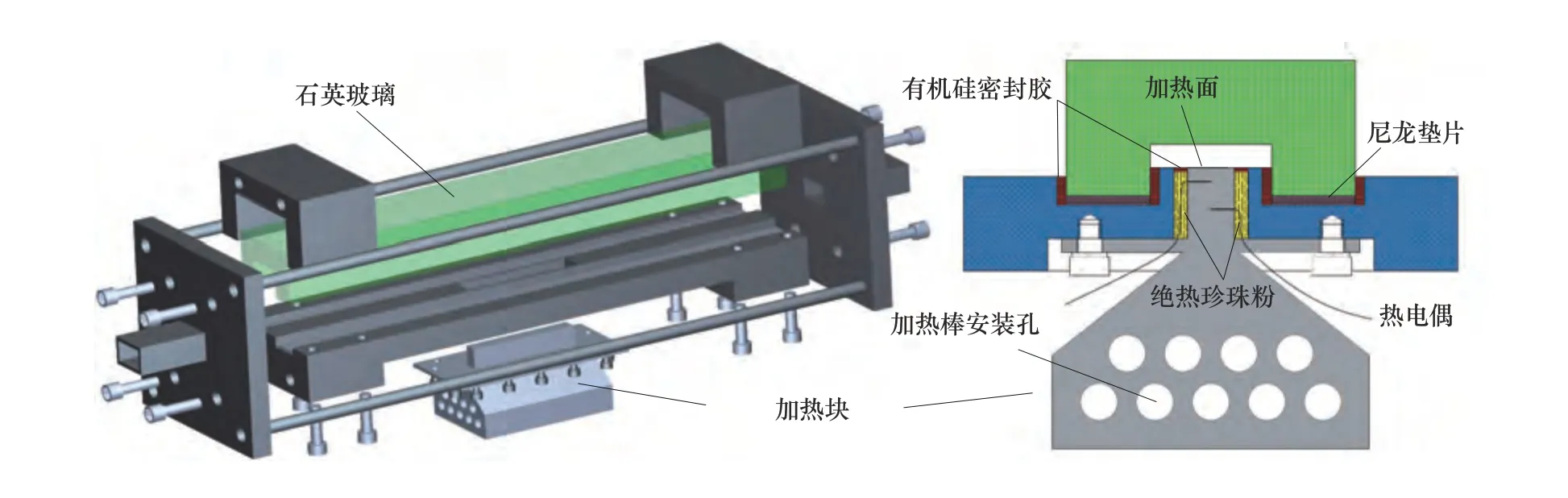
图2 矩形实验段示意图Fig.2 Details of the test section assembly

1.2 误差分析

直接测量参数的误差可由传感器的精度获得，间接测量参数的误差可通过相关的直接测量参数的误差来求解，假设间接测量参数与直接测量参数的关系如下：

式中，δx1,δx2,…,δxn代表直接测量参数的不确定度。间接测量参数与直接测量参数的误差如表1 所示。

表1 间接测量参数与直接测量参数的误差Table 1 Measured and calculated parameters and their uncertainties

气泡浮升直径的测量原理如图3 所示，采用气泡的长轴dl与短轴ds的平均值作为气泡的尺寸，气泡的长轴、短轴均以图中方式进行测量，由于气泡浮升远离壁面的时刻很难确定，本文以浮升前的气泡直径dpre和浮升后的气泡直径dpost的平均值作为气泡浮升直径Dl。

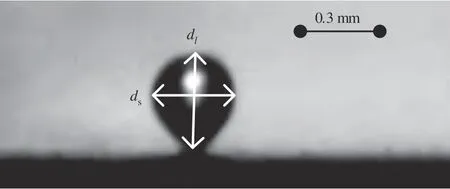
图3 气泡浮升直径测量原理Fig.3 Bubble measurement at the moment of bubble lift-off

由于受到光线的折射、散射等的影响，气泡浮升直径的不确定度δlr为0.028 mm，气泡浮升直径的B型不确定度可通过式(3)计算：

其中，δA是A 型不确定度;δB是B 型不确定度;δc是标准不确定度;y1,y2,…,yn是实验测量样本，yˉ是这些测量值的平均值;n是实验测量的样本数量。

2 实验结果及理论分析

2.1 实验结果

本文研究了系统压力Psys、壁面过热度ΔTsup、流速v以及液体过冷度ΔTsub对气泡浮升直径的影响。图4展示了在保持系统压力121 kPa、过冷度12 K 和过热度约11 K 时，气泡在不同流速下的生长、脱离和浮升过程。从该图可以看出，气泡在生长初期会迅速长大，然后缓慢生长。在气泡缓慢生长过程中，气泡先脱离核化点沿着加热面滑移，最后浮升远离加热面。在高流速下，气泡均出现了先滑移然后浮升远离加热面的现象。

图5～图7展示了不同的系统压力、壁面过热度、流速以及液体过冷度对气泡浮升直径的影响。气泡浮升直径随着壁面过热度的增加而增大，从气泡力平衡的角度看，这是因为较高的壁面过热度可加速气泡的生长，而较快的生长速率会增大气泡非对称生长力，该力会阻止气泡的浮升。因此，该力使得气泡浮升直径变大。

图5为不同速度下气泡浮升直径随过热度的变化关系。从图中可看出流体速度越大，气泡的浮升直径越小。这是因为流体速度的增大会导致剪切升力的增大，从而引起气泡提前浮升远离壁面。同时，流速的增大，可以减弱气泡的生长速度，气泡生长力也会变弱，从而气泡提前浮升远离壁面。因此，气泡浮升直径随着流速的增大而变小。

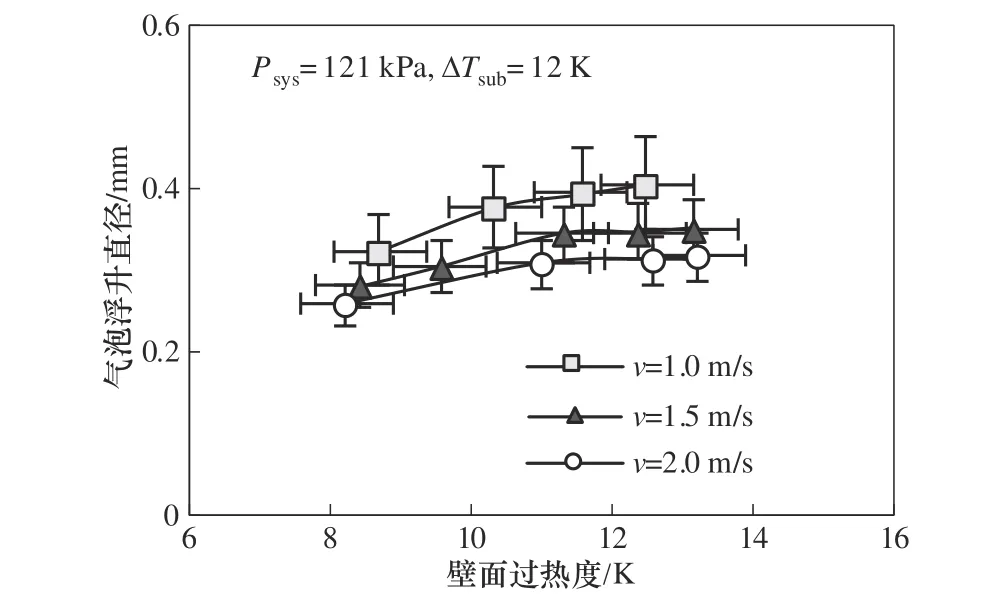
图5 不同流速下气泡浮升直径随过热度的变化关系Fig.5 Relationship between bubble lift-off diameter and wall superheat under different flow velocities

在系统压力121、169 和232 kPa 下，气泡浮升直径随壁面过热度的变化如图6所示，由图可看出，气泡浮升直径随系统压力的增大而降低。由于气泡蒸汽的密度及饱和温度随着系统压力的增大而增大，在高压下，产生相同体积的气泡需要更多的能量，这会导致气泡生长速度随着系统压力升高而变慢，气泡非对称生长力变小。因此，气泡浮升直径会随着系统压力的增大而降低。

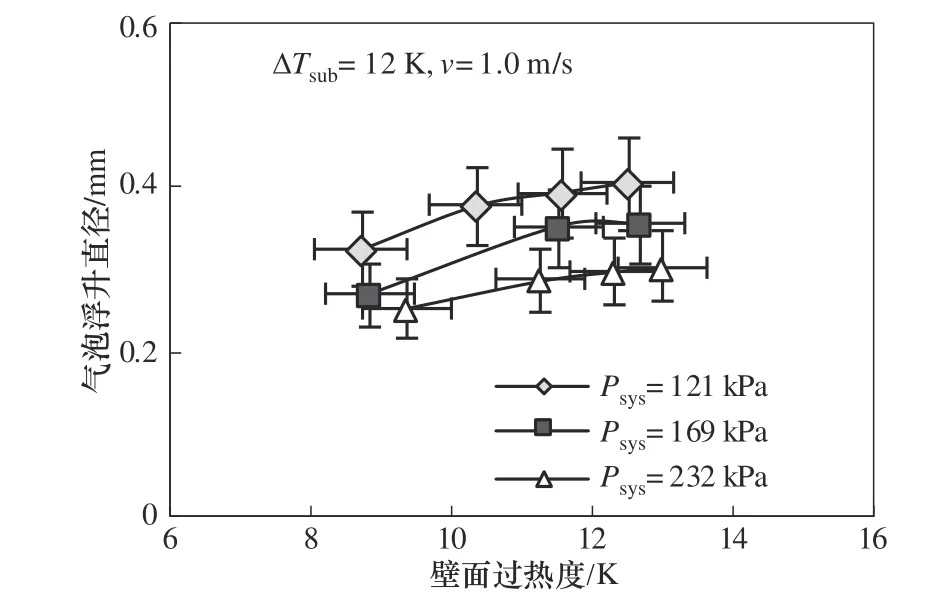
图6 不同压力下气泡浮升直径随过热度的变化关系Fig.6 Relationship between bubble lift-off diameter and wall superheat under different system pressures

图7 展示了在不同过冷度（5、8、12 和15 K）下，气泡浮升直径随壁面过热度的变化。从图中可看出，气泡浮升直径随过冷度的增大而减小，这是因为较高的过冷度会导致气泡顶部较快的冷凝速率，气泡体积变小，同时气泡非对称生长力也会变小，从而使得气泡提前浮升远离壁面。因此，气泡浮升直径随着过冷度的增大而减小。还可以发现，随着壁面过热度的增加，在加热面附近的过热层厚度会增大，从而会降低气泡顶部的冷凝效果，降低过冷度对气泡尺寸的影响。因此，在高过热度下，气泡浮升直径会随着壁面过热度的增大而缓慢增加。

2.2 理论分析

气泡在加热面上的受力如图8 所示，具体的受力模型如表2 所示。图8 中，x方向平行于加热面，y方向垂直于加热面，气泡在x方向和y方向的受力之和为：

表2 气泡受力模型［3］Table 2 Various forces for force balance model［3］

图7 不同过冷度下气泡浮升直径随过热度的变化关系Fig.7 Relationship between bubble lift-off diameter and wall superheat under different subcooling

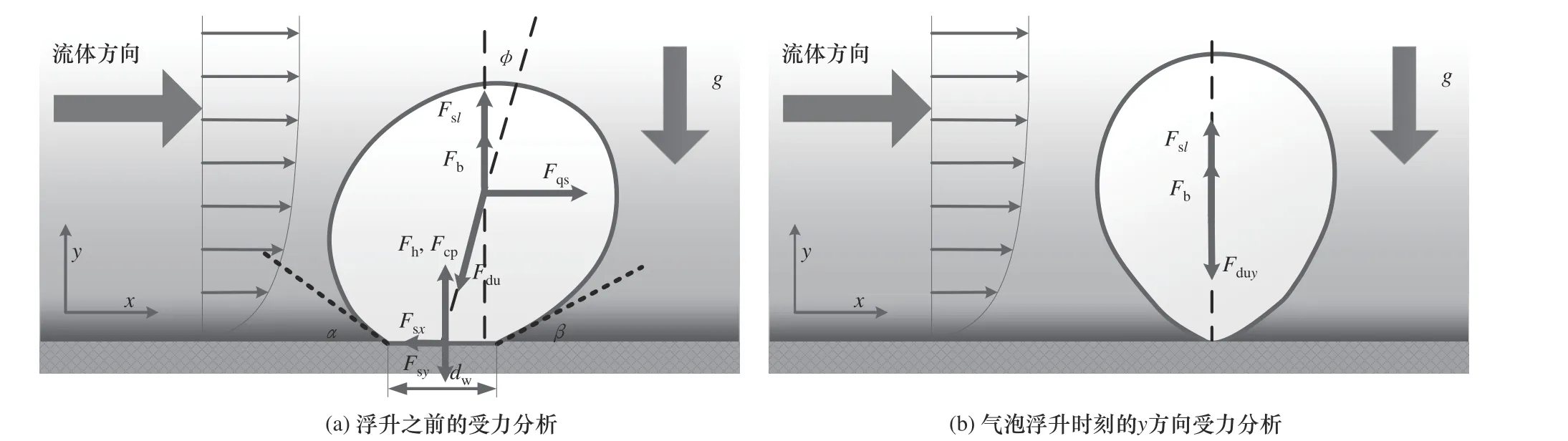
图8 气泡受力分析示意图Fig.8 Diagrammatic sketch of forces acting on vapor bubble

式中，Fsx、Fqs及Fdux分别代表x方向的表面张力、准稳态曳力及非对称生长力（非对称气泡生长引起的非稳态拖曳力）；Fsy、Fduy、Fsl、Fb、Fh和Fcp分别代表y方向的表面张力、非对称生长力、剪切升力、浮力、水动力和接触力。

气泡的滑移与脱离可通过式(6)和式(7)进行判断，当x方向力平衡被打破时，气泡在加热面上滑移。当y方向力平衡被打破时，气泡浮升远离加热面。因此，气泡浮升直径可通过式(7)获得。

当气泡浮升远离壁面时，气泡与壁面的接触直径几乎等于零，基于此，这里假设气泡接触直径dw等于0，那么在y方向的力平衡模型中，表面张力Fsy、水动力Fh、接触力Fcp均等于零。因此，在气泡浮升的时刻，y方向的受力模型可简化为：

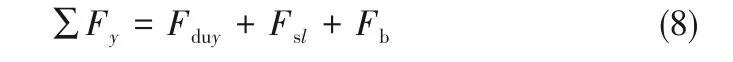
由式(8)可看出，该方向的力平衡模型仅受气泡非对称生长力Fduy、剪切升力Fsl和浮力Fb的影响，气泡生长模型和近壁面模型采用文献[3]中的模型。这里应注意，在气泡浮升之前，通常会发生气泡滑移现象，因此，应考虑气泡滑移的速度对气泡生长力及剪切升力的影响，在该力模型中，速度应为相对速度Ur，但是由于本文中研究的流速较高，气泡滑移速度相对于主流体速度较小，可以忽略，而在低流速下，应考虑气泡滑移速度的影响。其中，Zeng 模型[18]和本文采用的气泡生长模型[3]见表3。

表3 气泡生长模型Table 3 Models of bubble growth rate

当力平衡模型y方向的力之和大于0时，通过该力平衡模型，可预测出气泡浮升直径的大小。图9展示了Zeng 模型[18]和本文力平衡模型的预测值与浮升直径的实验值的对比。从图中可以看出，Zeng模型对气泡浮升直径的预测值与实验值的平均相对误差为22.38%，而本文建立的力平衡模型可以准确预测气泡浮升直径，大部分数据预测偏差都分布在30%以内，平均相对误差为12.25%。本文的力平衡模型预测精度提高的主要原因是本文采用的气泡生长模型[3]考虑了微液层蒸发、过热层蒸发以及过冷层冷凝对气泡生长的影响，该气泡生长模型更适合预测过冷流动沸腾中的气泡生长过程。

2.3 气泡浮升直径经验模型

气泡浮升直径的经验模型相比于力平衡模型，公式简单，易求解，在工程中应用广泛。为便于工程应用，本文采用量纲分析法对气泡浮升直径数据进行拟合。从力平衡模型和气泡生长模型[3]可知，气泡浮升直径与无量纲数ρ*、JaN,w、JaN,sub、Re及Pr有关。因此，气泡浮升直径的无量纲形式可表达为：

图10展示了采用Basu模型[5]和本文新拟合经验模型对气泡浮升直径预测值与实验值的对比情况。从图中可看出，Basu 模型的预测值与实验测量值的平均相对误差为68.21%，该模型预测的气泡浮升直径普遍偏大。原因有两点：一是Basu 模型属于经验模型，采用的气泡浮升直径的系统压力为103 kPa，没有考虑系统压力对气泡浮升直径的影响，从本文实验数据可看出，气泡浮升直径随着系统压力的增大会变小，而本文实验的系统压力较高，气泡浮升直径较小。二是Basu 模型由竖直通道内的气泡浮升直径拟合得到，在竖直通道内，重力方向与加热面方向平行，与气泡浮升远离壁面方向垂直，这种情况下，竖直通道的重力不会促使气泡浮升远离加热面，竖直通道内的气泡浮升直径会比水平通道内的气泡浮升直径大。因此，Basu 模型的预测值较实验值偏大。本文新拟合的经验模型可以准确地预测气泡浮升直径，预测结果与实验结果平均相对误差为6.80%。在研究的工况范围内，预测精度高于力平衡模型。新模型主要适用于本实验覆盖的工况范围，该范围涵盖了发动机水腔沸腾区域的大部分工况，满足发动机需求。但是拟合的公式均有一定的局限性，在应用该模型时，应注意其适用范围。依据本实验的工况范围，可以得到新拟合的气泡浮升直径经验模型的适用范围，见表4。

表4 本文气泡浮升直径经验模型适用范围Table 4 Range of parameters for the new bubble lift-off diameter model

3 结 论

针对发动机缸盖沸腾区域的冷却通道，本文设计了一个水动力相似的矩形实验通道，搭建了过冷流动沸腾可视化实验循环系统。基于该实验系统，探究了不同工况对气泡浮升直径的影响，并建立了气泡浮升直径的力平衡模型和经验模型，主要结论如下。

(1) 在高流速下，加热面上的气泡会先出现滑移，然后浮升远离壁面，气泡浮升直径随着系统压力、流速以及过冷度的增大而变小，随着壁面过热度的增大而增大。

(2)本文建立的气泡浮升直径的力平衡模型可以准确预测气泡浮升直径，可从力平衡的角度剖析气泡浮升机理，该力平衡模型的预测值与实验值的平均相对误差为12.25%。

(3)本文建立的气泡浮升直径经验模型的预测值与实验值吻合较好，平均相对误差为6.80%，满足内燃机领域的工程需求。

符 号 说 明

cp——比热容，J/(kg·K)

Dd，Dl，Dm——分别为气泡脱离直径、气泡浮升直径、气泡最大直径，m

dl，ds，dw，dpre，dpost——分别为气泡长轴、气泡短轴、气泡接触直径、气泡浮升前直径、气泡浮升后直径，m

g——重力加速度，m/s2

P——压力，Pa

Pr——Prandtl数

R——气泡半径，m

Ṙ——气泡半径一阶导数，m/s

R̈——气泡半径二阶导数，m/s2

Re——Reynolds数

T——温度，K

U——流速，m/s

α——前进接触角，rad

β——后退接触角，rad

δ——不确定度

υl——运动黏度，m2/s

ρl，ρv——分别为液体、气体密度，kg/m3

σ——表面张力，N/m

下角标

b——气泡

l——液体

sat——饱和

sub——过冷

sup——过热

v——气体