特征变量选择结合SVM的耕地土壤Hg含量高光谱反演

郭云开,张思爱，王建军，章 琼，谢晓峰

(1.长沙理工大学 交通运输工程学院，长沙 410076; 2.长沙理工大学 测绘遥感应用技术研究所，长沙 410076; 3.清远市土地整理中心，广东 清远 511518;4.广州城建职业学院 建筑工程学院，广州 510925)

随着工业化城镇化的快速发展，土壤重金属污染问题变得日益显著[1-2]。汞作为一种毒性极强的金属，对环境与生态系统的持续性、严重性危害已引起全球性的关注。传统的土壤重金属含量监测方法精度高，但费时费力且难以实现大面积重金属含量动态监测[3-5]。高光谱技术具有无损、高效、低成本等优点，为快速获取土壤重金属信息提供有效手段，引起国内外学者对土壤重金属高光谱反演的广泛研究。

Kooristra L等通过对莱茵河区域进行土壤重金属Zn,Cd含量反演，发现偏最小二乘回归模型能够获得较好的精度[6]。涂宇龙等通过主成分分析(PCA)与皮尔森相关系数(PCC)提取重金属铜元素的特征波段，并运用逐步回归法进行建模，发现PCA特征提取能有效提升土壤Cu含量预测精度[7]。滕靖等通过对西范坪矿区土壤Cu元素进行研究，利用逐步回归法和皮尔逊相关系数分别提取土壤Cu的特征波并组成特征变量集，取得较好的预测效果[8]。袁自然等利用竞争性自适应重加权算法进行光谱粗选，并通过PSO -SVM对土壤砷(As)含量估算研究，结果表明，基于优化后的SVM模型预测精度具有明显提高[9]。

虽然对于土壤重金属已有大量研究，但由于土壤重金属与原始光谱反射率敏感性弱，且光谱数据冗余等因素，导致反演精度不高，对数据进行降维在一定程度上能有效提高模型精度。不同特征变量提取方法所得变量有所不同，其模型精度也会受到影响[10]。目前，已有研究中光谱特征变量提取方式和反演模型都有待进一步改进。

文中针对土壤重金属光谱特征弱和光谱数据冗余问题，以湖南省衡东县某工业区周边耕地为对象开展土壤重金属Hg的高光谱估算模型研究。首先对原始光谱数据进行预处理，利用一阶微分(FD)、二阶微分(SD)、倒数对数(RL)和多元散射校正(MSC)进行光谱变换，分别与重金属Hg元素进行相关性分析选取最优变换光谱，再利用迭代保留信息变量法((Iteratively Retains Informative Variables，IRIV)、皮尔森相关系数(PCC)和随机蛙跳算法(Random frog)进行光谱特征选取，分别建立SVM与GWO-SVM土壤重金属Hg含量高光谱反演模型，找出最优反演路径，提高预测精度。

1 数据与方法

1.1 研究区概况与数据获取

衡东县位于衡阳市东北部地区中心城镇，地貌主要以丘陵为主，气候温和湿润，雨量充沛，交通便利，地理位置优越。近年来，随着农业生产结构调整，形成以茶油、油菜为主的多个产业种植带。此外，研究区工业发达，具有大量工业企业，且以化工、重金属等产业为主，使当地生态环境受到了严峻挑战。因此，对研究区耕地土壤重金属污染情况的研究已迫在眉睫。本次试验研究于2019年6月进行，每个样本实地采集以“S”型曲线确定5个土壤样点，共采集88个样本。土壤样本采集过程中，对土壤样品进行密封、标记等处理。实验分析前，将土壤样品在阳光下自然风干，研磨并剔除土壤中杂质，最后使用100目尼龙筛过滤。对每个土壤样本分别通过化学方法测定土壤重金属Hg含量和使用AvaField-3波谱仪(波段范围为300～2 500 nm)进行土壤高光谱采集。土壤Hg含量的描述性统计结果如表1所示。

表1 土壤Hg含量描述性统计

1.2 数据预处理与相关性分析

光谱采集过程中易受仪器噪声、水分、环境等因素影响，导致光谱曲线含有较多噪声，影响土壤重金属预测精度[11]。本次研究去除边缘噪声较大的土壤光谱波段300～400 nm和2 300～2 500 nm，并对原始光谱数据(400～2 300 nm)进行SG平滑处理，通过10 nm重采样(RS)对光谱信息进行数据降维，采用FD、SD、RL和MSC等光谱变换处理，使土壤光谱特征更明显。运用SPSS软件对以上光谱数据与土壤重金属Hg含量进行相关性分析，如图1所示。RS与Hg的相关性总体呈正相关且相关性不明显，RL则呈负相关且相关性略有提高，FD和SD与Hg的相关性 900 nm波段以后普遍较低。综上可见，FD光谱变换相关性提升效果最佳，在580～1 030 nm、1 800～2 080 nm波段相关性总体较好，且在1 810 nm相关性值最高为0.394。因此，文中选取FD变换光谱作为后续特征波段提取研究。

1.3 研究方法

1.3.1 迭代保留信息变量法

IRIV是一种新型的特征变量提取方法，利用变量的随机组合进而考虑到变量之间的相互作用，将变量划分为强信息变量、弱信息变量、无信息变量和干扰信息变量[12-13]。基本步骤主要将m个样本n维变量的一阶微分变换光谱数据转换为含有相同数量的0和1矩阵X，其中1和0表示变量是否用于建模，通过交叉验证均方根误差(RMSECV)去评估包含任意变量i和未包含i在模型中的重要性。基于每个变量的重要性程度进行算法迭代，直到只剩下强信息变量和弱信息变量的新变量子集P。通过对变量集P进行反向消除策略，最终获得最优特征变量。

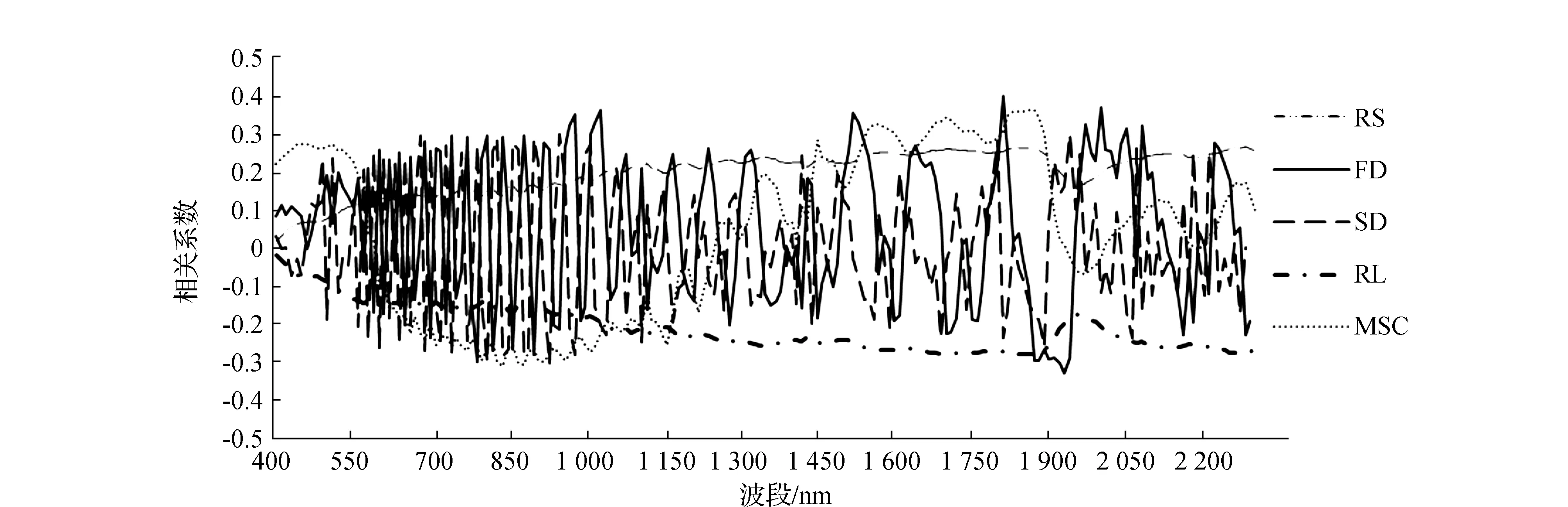
图1 光谱数据与Hg元素相关性分析

1.3.2 随机蛙跳算法

随机蛙跳是一种对高维变量数据进行特征选择的新方法，其利用少量变量迭代进行建模，并输出每个变量选择的可能性，根据不同需求选取可能性较大的变量作为特征变量[14]。其主要步骤如下：

1)随机初始化包含Q个变量，得到一个变量集V0。

2)通过初始变量集V0提出一个包含Q*个变量的候选变量集V*，根据一定的概率选择V*作为V1，并利用V1替换V0。通过循环此步骤，直至完成N次迭代结束。

3)计算每个变量的选择概率，该概率可以用作变量重要性的度量。

1.3.3 皮尔森相关系数

皮尔森相关系数(PCC)是一种普遍使用的线性相关系数，一般使用r表示。它能够反映两个变量X和Y的线性相关程度，其r值为-1～1之间，绝对值越大表明相关性越强。其算式表达如下：

(1)

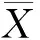
1.3.4 灰狼算法优化支持向量机

支持向量机是Vapnik提出的一种基于统计学理论的新型的机器学习方法，其常用于小样本的非线性问题[15]。灰狼优化算法(Grey Wolf Optimizer，GWO)是Mirjalili等受灰狼捕食启发在2014年提出的一种新型群体智能优化算法[16]。文中采用GWO算法对SVM惩罚因子c和核函数参数g进行寻优，灰狼优化算法利用狼群严格的等级制度(α,β,δ和ω)，不断更新各等级狼群位置寻找猎物，获取全局最优解。其算法步骤流程如下：

1)初始化参数：狼群数量n=20，最大迭代次数N=400，设定惩罚因子c和核函数参数g的取值范围。

2)随机生成灰狼群，每头狼个体位置受参数c和g影响，通过对训练集学习计算每头狼相应的适应度值，利用适应度值对狼群进行等级划分，并对狼群位置进行更新。

3)计算每头狼在新位置的适应度值，并与上一次迭代最优适应度值比较，选取最优值，超过最大迭代次数时结束，选取全局最优位置即为参数c和g的最优值，否则返回第二步继续寻优。

4)利用寻优后的参数c和g进行SVM的回归预测。

1.4 模型精度评价与研究技术路线

采用决定系数(R2)、均方根误差(RMSE)和平均绝对误差(MAE)3个指标对两种预测模型进行精度评价。其中决定系数R2越大，模型的预测效果越好，RMSE和MAE越小，说明预测值与实测值越接近，其模型鲁棒性越高。文中研究技术路线如图2所示。

图2 研究技术路线流程

2 试验分析

2.1 特征波段选取

由于高光谱数据信息波段多，数据冗余问题严重影响反演精度，为避免数据冗余并提高模型反演精度，文中使用IRIV、Random Frog和PCC 3种特征提取方法对FD变换光谱进行波段提取。

IRIV算法中的交叉验证次数为5，最大主因子为10，共有190个光谱波长变量，随着迭代次数的增加，保留的变量会相应的减少，其迭代保留变量数如图3所示。本次研究共进行6次迭代，在第7次迭代时趋于饱和，每次迭代所保留变量数分别是190、82、42、25、21和20，再对剩余变量进行反向消除，最后筛选获得16个与重金属Hg的最优光谱特征变量，其中强信息变量为5个，均为近红外变量(1 040 nm、1 990 nm、2 220 nm、2 240 nm、2 280 nm)，弱信息变量为11个，其中可见光变量2个(600 nm、620 nm)，近红外变量9个(1 000 nm、1 090 nm、1 560 nm、1 590 nm、1 610 nm、1 620 nm、1 730 nm、2 100 nm、2 110 nm)。

Random Frog算法根据每个变量具有不同的选择概率对光谱变量进行提取，其变量选择概率如图4所示，变量数在120左右(对应光谱波段1 590 nm)，选择概率达到最高。本次研究通过提取选择可能性排名前10的光谱变量作为特征波段，其全部集中在近红外波段(1 030 nm、1 040 nm、1 320 nm、1 340 nm、1 590 nm、1 780 nm、1 940 nm、1 960 nm、2 080 nm和2 180 nm)。

利用皮尔森相关系数对重金属Hg含量与一阶微分变换光谱进行相关性分析如图5所示，当显著性水平P<0.05和P<0.01时，其相关系数在0.208和0.273时为显著相关和极显著相关。文中通过选取显著性水平P<0.01的光谱变量作为特征波段，在1 810 nm处达到最大相关值0.394；其特征波段为690 nm、740 nm、770 nm、790 nm、810 nm、840 nm、880 nm、900 nm、920 nm、970 nm、1 010 nm、1 020 nm、1 030 nm、1 520 nm、1 530 nm、1 540 nm、1 810 nm、1 870 nm、1 880 nm、1 900 nm、1 910 nm、1 920 nm、1 930 nm、1 940 nm、1 970 nm、2 000 nm、2 040 nm、2 050 nm、2 080 nm和2 200 nm。

图3 IRIV迭代保留变量数

图4 Random Frog特征波段提取

图5 Hg含量与FD变换光谱相关性

2.2 SVM回归预测

本次试验利用3种特征提取方法分别提取土壤重金属Hg含量光谱特征波段，通过以上研究可得，IRIV、Random Frog和PCC分别提取16、10和30个特征波段用于建模。本次实验共采集88个样本，其中选取60个作为建模样本，其余28个作为验证样本，利用特征波段作为光谱参量，建立SVM土壤重金属含量反演模型。采用决定系数、均方根误差和平均绝对误差综合评价两种模型性能，如表2所示。其中基于PCC特征提取的建模集R2为0.835，RMSE为0.091，MAE为0.018，验证集R2为0.833，RMSE为0.086，MAE为0.017，模型预测效果最好；基于Random Frog特征提取的建模集R2为0.804，RMSE为0.094，MAE为0.017，验证集R2为0.654，RMSE为0.118，MAE为0.018，模型预测效果相对较差；基于IRIV特征提取的建模集R2为0.767，RMSE为0.097，MAE为0.018，验证集R2为0.778，RMSE为0.093，MAE为0.018，模型预测效果较好；SVM模型实测值与预测值散点图如图6(a)、图6(c)、图6(e)所示。

2.3 GWO-SVM回归预测

通过对一阶微分变换光谱进行IRIV、Random Frog和PCC特征波段提取，利用特征波段作为自变量，土壤重金属含量作为因变量，建立GWO-SVM回归模型，建模结果如表3所示。其中基于IRIV特征提取的建模集R2为0.908，RMSE为0.090，MAE为0.019，验证集R2为0.894，RMSE为0.082，MAE为0.016，模型预测效果最佳；基于Random Frog特征提取的建模集R2为0.859，RMSE为0.085，MAE为0.018，验证集R2为0.856，RMSE为0.080，MAE为0.015，模型预测精度相对较低；基于PCC特征提取的建模集R2为0.864，RMSE为0.086，MAE为0.017，验证集R2为0.876，RMSE为0.078，MAE为0.015，模型预测效果较好。相较于SVM回归模型，GWO-SVM模型在IRIV和Random Frog特征提取的验证集模型R2分别提高0.116和0.202，RMSE和MAE相应降低；在PCC特征波段提取的验证集模型R2略有提升，RMSE和MAE相应降低。GWO-SVM模型估测结果如图6(b)、图6(d)、图6(f)所示，从图中可知，其实测值与预测值趋势基本一致，说明经过灰狼算法优化后的支持向量机模型预测精度与稳定性得到明显改善，满足实际预测要求。

表2 SVM回归模型验证系数

表3 GWO-SVM回归模型验证系数

3 讨 论

本次实验主要针对耕地土壤重金属Hg含量高光谱估算研究，通过重金属Hg含量与变换光谱数据进行相关性分析可得，一阶微分光谱变换与Hg元素相关性整体最优，这是由于微分技术能够较好去除光谱曲线漂移现象和部分线性的背景干扰，更好地提高光谱与重金属之间敏感光谱特征参数[17]。 对比3种特征波段提取方法，IRIV的复杂程度较高且运算时间较长，在波段数量上，IRIV、Random Frog和PCC方法分别提取16、10和30个特征波段，在很大程度上减少数据冗余。此外，对比3种方法提取下的光谱特征波段，主要分布在近红外波段，少量在可见光波段，说明Hg元素的光谱敏感波段主要分布在近红外波段。在模型上，通过灰狼算法对支持向量机的核函数g和惩罚因子c进行优化，对比未优化的支持向量机回归模型，在一定程度上提高回归模型的预测精度和稳定性。在建模结果上，基于IRIV特征提取下的GWO-SVM模型建模效果最优，其验证集R2为0.894，RMSE为0.082，MAE为0.016。说明IRIV特征提取能够有效去除无信息变量和干扰信息变量保留强信息变量和弱信息变量，降低模型误差，提高模型预测精度。综上可得，IRIV结合GWO-SVM模型能够快速准确预测土壤重金属含量。

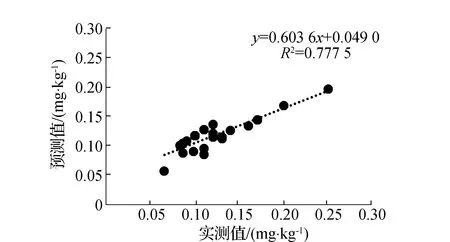
(a)IRIV-SVM

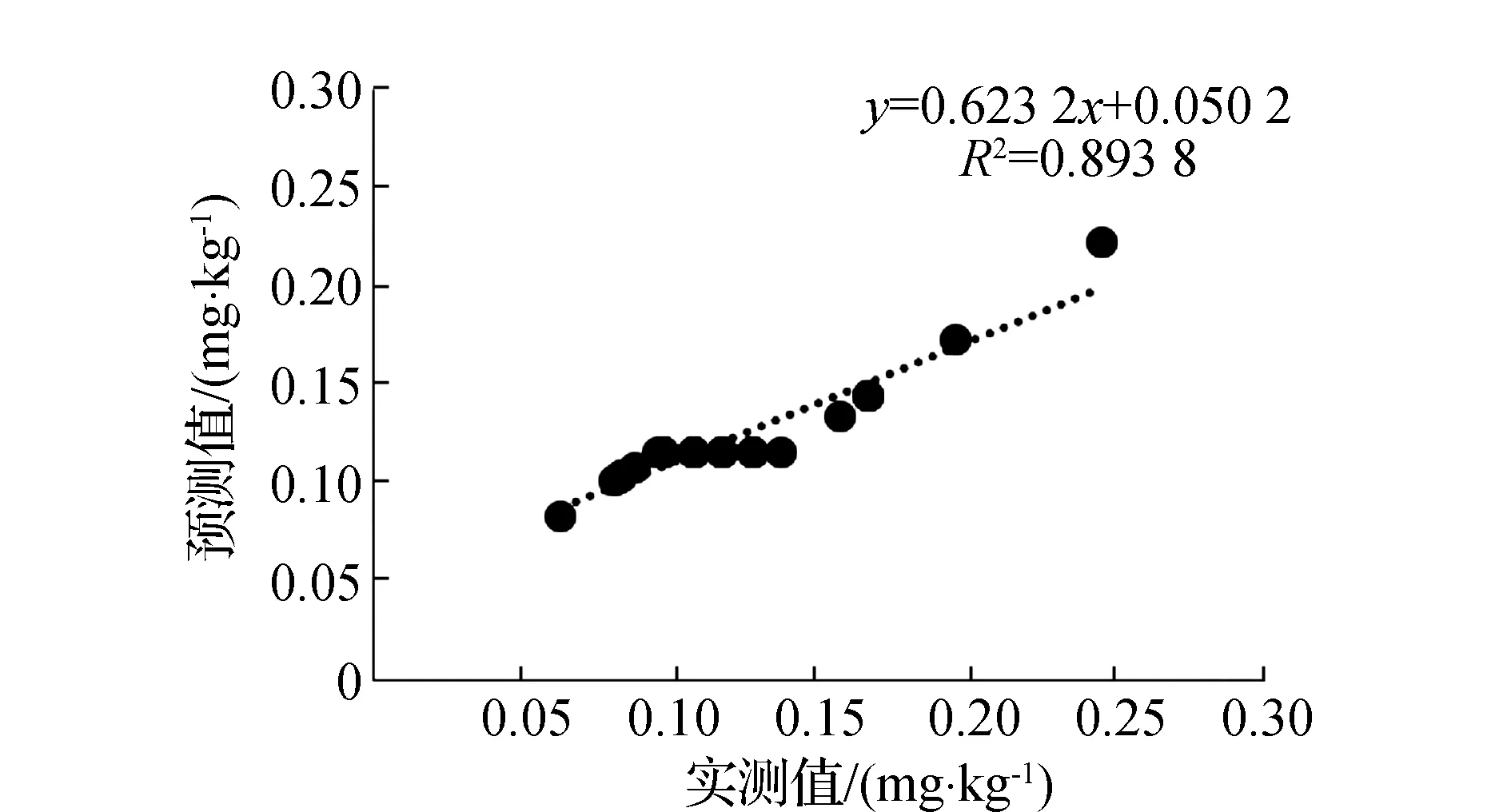
(b)IRIV-GWO-SVM

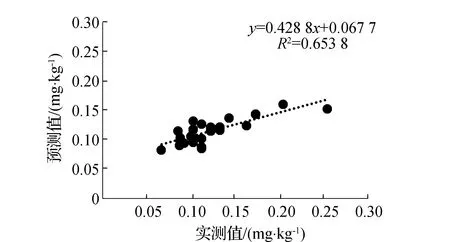
(c)Random-Frog-SVM

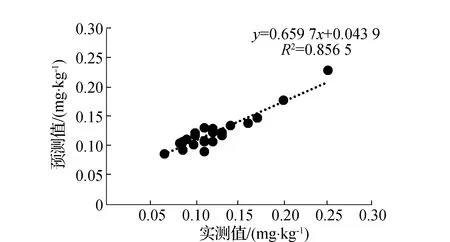
(d)Random-Frog-GWO-SVM

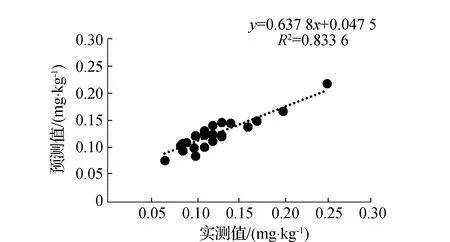
(e)PCC-SVM

(f)PCC-GWO-SVM

4 结 论

文中以湖南省衡东县某工业区周边耕地为研究对象，通过对光谱数据与土壤Hg元素进行相关性分析，使用不同特征提取方法进行光谱特征提取，采用SVM与GWO-SVM分别构建土壤重金属Hg含量高光谱反演模型。结果表明：1)通过对原始光谱进行不同光谱变换处理，发现一阶微分光谱变换后土壤光谱特征更明显，与土壤重金属Hg的相关性更高，在1 810 nm波段相关性值最高为0.394。2)通过IRIV、Random Frog和PCC方法分别提取16、10和30个特征波段，在很大程度上减少光谱数据冗余并保留有效变量信息，增强模型稳定性，提高模型预测精度。(3)对比两种模型，经过灰狼算法优化后的支持向量机在不同特征提取下的建模结果明显优于支持向量机模型，其中IRIV结合GWO-SVM模型精度最高。说明灰狼算法能够有效增强支持向量机性能，提高模型稳定性与预测精度，研究可为同类地区反演土壤重金属含量提供新的参考。