基于核密度估计和Copula函数的风、光出力场景生成
宋 宇 李 涵
基于核密度估计和Copula函数的风、光出力场景生成
宋 宇 李 涵
(国网江苏省电力有限公司检修分公司,南京 211102)
新能源的随机性、波动性及间歇性为电力系统规划带来困扰,对风、光出力的变化规律进行合理刻画,生成典型出力场景是新能源规划的常用方法。针对具有相关性的风、光出力典型场景难以生成的问题,本文首先应用非参数核密度估计法对大量样本数据进行拟合,并进行拟合优度及精度检验,得到风、光的核密度估计表达式,然后建立多种基于Copula函数的风、光电场出力联合分布模型,判断各个模型的拟合优度,结合各个模型的Kendall与Spearman相关系数,选取最优Copula函数作为风电、光伏联合概率分布,最后采用最优Copula联合概率分布生成风、光年出力场景。算例分析表明,所得的风、光年出力场景符合其相关性,在反映某地区风光实际出力时有更高的准确性,可为电力系统可靠性分析和电网规划提供参考。
核密度估计;Copula函数;场景生成;互补特性;差异系数
0 引言
以风电、光伏为代表的新能源发电存在显著差异性,如果不采取措施就直接接入电网,会对电网的可靠性和稳定运行造成很大影响。风电、光伏等间歇性能源的建模成为新能源消纳问题的基础研究课题。同一地区的风电场和光伏电站具有较强的统计学规律及相关性,而电力系统的中、长期规划均需基于风、光自身的出力特性,以大量场景基础进行分析计算,来评估规划方案的可行性和合理性。因此,考虑其相关特性,建立合适的风、光联合出力模型,生成典型场景,对电力系统规划有重要 意义。
当下很多研究人员尝试使用Copula理论研究风、光出力相关性的问题[1-3]。文献[4]首先提出一种基于Copula的计算风光出力联合概率分布的方法,然后利用聚类算法进行模型误差分析,该模型考虑了不同环境下二者的影响与变化关系,使风、光出力的预测准确性大大提高。文献[5]分析了传统Copula方法的不足之处,提出一种新的动态式的Copula函数模型,该模型计算了8组不同实例的动态相关性,验证了所提模型的准确性与合理性。文献[6]用阿基米德族Copula函数对多风电场联合出力进行建模,并用正态Copula函数进行比较,证明了阿基米德族Copula函数解决此类问题的优越性。
然而,现有仅建立单个Copula模型的方法无法可靠地验证所选取的Copula函数是否为模型中的最优函数,造成生成的典型出力场景与实际情况出入较大。因此,仍需对Copula函数进行研究与改进,选取最优Copula函数。
本文采用非参数核密度估计法对实际数据进行拟合,经拟合优度及精度检验后,得到风、光出力的核密度表达式。然后建立多种基于Copula函数的风、光电场出力联合分布模型,结合各模型的Kendall与Spearman相关系数,将各Copula分布函数与经验Copula函数比较,并判断与经验Copula函数的欧氏距离,选取最优Copula函数作为风电、光伏联合概率分布,从而生成风、光出力典型场景。算例分析表明,本文所提方法生成的风、光年出力场景符合其相关性,在反映地区风光实际出力时有较高的准确性。
1 核密度估计及模型检验方法
研究风速大小与光照强度概率分布模型时,通常采用两种方法,即理论分布模型与核密度估计法,前者基于参数,而后者基于非参数。基于参数估计的方法需要事先规定其符合的特定分布,一定程度上忽略了风速曲线与光照强度曲线本身具有的特征,导致参数分布模型拟合得到的结果很大程度地偏离数据实际分布[7]。非参数方法不需要提前知晓样本的模型,以已有样本为基础即可挖掘出数据的分布特征[8]。
1.1 核密度估计法


式中:为样本数量;为窗宽;(·)为核函数。
核密度估计法不需要事先假设样本数据所符合的分布,可以直接对风电功率与光伏功率的数据进行非参数估计,从而得到各自的概率密度函数。
除了核函数会影响核密度估计的结果,窗宽也是一个需要优化的参数。其估计值与实际值的积分方均误差为

式中,为权值矩阵。将式(2)最小化得出的o代入式(1)取出可得到总体的核估计值。
1.2 模型检验方法
1)拟合优度检验
在完成概率密度的拟合之后,需要对拟合的效果进行检验。通过对拟合效果的检验,可以衡量出各个拟合方法对原始数据的拟合优劣程度,从而选取出最佳拟合函数。常用的检验方法有两种[9],分别为Pearson2与K-S(Kolmogorov-Smirnov)。
(1)Pearson2


式中:v为第个区间内的样本数量;p为其落在第个区间内的理论值。


式中,(·)表示事件发生的概率。

(2)Kolmogorov-Smirnov
Pearson2需要将样本空间划分成个子空间,导致检验结果随区间选取的变化而变化,而Kolmogorov-Smirnov检验具有良好的适用性。

基于原始样本,求得经验累积分布函数F()为
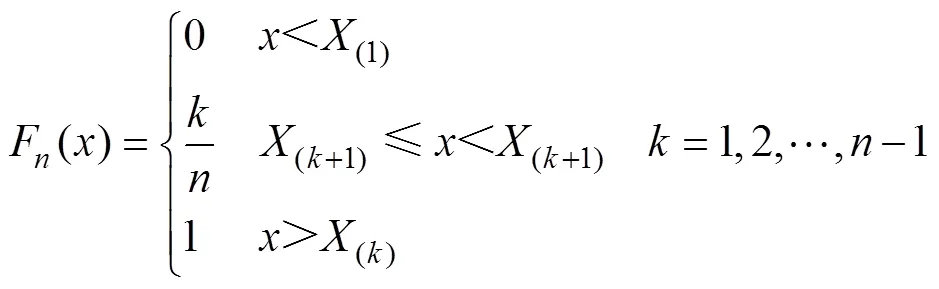
基于理论累积分布0()和经验累积分布F()之间的最大垂直差距定义为检验统计量D,有

式中,为第个抽样区间。
理论分布模型的参数可由实际历史数据得到,在此情况下,当一个理论分布在检验中被拒绝时,则K-S检验产生的误差相对较小。
2)拟合精度检验
拟合精度检验是从定量的角度去衡量风光出力概率模型与实际出力的频度分布曲线之间的不同。采用平均百分比误差(mean absolute percentage error, MAPE)与方均根误差(root mean square error, RMSE)两个指标衡量模型的拟合精度。


式中:为区间个数;oi、gi分别为风电和光伏标准化输出功率正交级数密度分布和直方图在第个区间的概率。
2 基于Copula理论的风光出力相关性建模及出力场景生成
2.1 Copula相关理论
1)Copula函数与相关系数
Copula的表达式为

常见的Copula有两个族,分别为阿基米德Copula与椭圆Copula。阿基米德Copula函数最常见的三种为Gumbel Copula、Clayton Copula和Frank Copula,椭圆Copula函数主要包括正态Copula和t-Copula两种。
相关系数用以反映变量之间的线性相关程度。常用的相关系数包括Kendall与Spearman秩相关系数[9]。
2)Copula函数的最优选择
由于Copula函数的类型众多,无法直接选取最优Copula,因此需对其进行拟合优度判别,从而选取最优函数。常用的方法包括函数图像判别法、相关系数判别法及欧氏距离判别法。
(1)函数图像判别法是将各Copula函数概率密度函数图像与样本数据的概率密度函数进行比较,图像最为接近的即为最优Copula函数。
(2)相关系数判别法是通过Kendall秩相关系数、Spearman秩相关系数判别其拟合优度。将各类Copula函数的秩相关系数与样本数据的秩相关系数相比较,数据越接近,其拟合优度越好,相应的Copula函数即为最优。
设具有相关性的风电场和光伏电站的出力分别为和。(1,1)和(2,2)是其出力(,)的任意两个出力样本观测值,两个值相互独立。如果(1,1)·(2,2)>0,则称(1,1)和(2,2)具有一致性;如果(1,1)·(2,2)<0,则称(1,1)和(2,2)具有不一致性。



(3)欧式距离判别法是用各Copula函数与样本数据的经验Copula函数的欧式距离比较,欧式距离越小,则Copula函数的拟合优度越好。

利用平方欧式距离选取最优Copula函数。平方欧式距离的定义为


2.2 风光场景生成与互补特性
1)基于蒙特卡洛的风光出力静态场景生成
选取了最佳Copula函数之后,应对Copula函数进行采样,从而生成大量样本,其主要步骤如 下[11-14]:
(1)在[0, 1]区间内随机产生数字1,2,…,a。
(2)令第一个随机变量边缘分布函数值1=1,根据2.1节中选定好的Copula函数来求得第二个随机变量边缘分布函数值2,即求式(14)的解。

(3)对于第个随机变量的边缘分布函数值u,即求式(15)的解。

(4)重复上述步骤(1)、(2)、(3)次,则可以得到组个随机变量的边缘分布函数值。
在对风电与光伏出力进行分析计算时,在步骤(5)的反函数运算中,首先基于Copula联合概率密度分别求出二者的边缘分布函数,然后再分别进行反函数的运算。通过这种计算方式,使所生成的场景充分考虑了风光出力的相关性。场景生成步骤如图1所示。

图1 风电出力与光伏出力的场景生成步骤
利用场景生成得到的数据量庞大,且各个场景之间相似度高。为实现相近场景的有效合并,采用后向缩减法[15](backward reduction, BR)进行场景缩减。基于后向缩减法的场景缩减流程如图2所示。

图2 基于后向缩减法的场景缩减流程
2)风光互补特性指标
采用差异系数(coefficient of variation, CV)来表征风光出力的互补特性,CV的定义为[16]


从式(16)可以看出,CV越小,风电与光伏所共同输出的功率越平稳,风光互补特性就越好。





3 算例分析
以某地区2020年全年的风速、光强为例,风速与光强的数据采样间隔为1h。采用正态分布、威布尔分布及核密度估计分别对风速数据进行拟合,正态分布、威布尔分布的参数采用极大似然估计来确定,风速参数拟合结果见表1,拟合效果如图3所示。
表1 风速参数拟合结果

这三种方法的拟合优度及拟合精度的检验结果见表2。
表2 不同拟合方法的拟合优度与拟合精度检验结果

其中,Pearson2的临界值为21.598,K-S的临界值为0.006 5。
威布尔分布与正态分布拟合相当,MAPE与RMSE的值接近,且均能通过Pearson2的检验,相对来说,正态分布的效果更优一些,但均未能通过K-S检验。而非参数核密度估计各项检验标准的值均远远小于参数估计的值,其拟合的效果更优。
对光照数据采用同样的方法进行处理,对比Beta分布与非参数核密度分布的拟合情况,参数拟合结果见表3,拟合效果如图4所示。由于Beta分布是定义在[0, 1]区间内的连续概率分布,因此此处将光照强度进行归一化处理。
表3 光照强度参数拟合结果

从图4中可以看出,核密度估计的拟合效果要远远优于Beta分布的拟合效果。
综上所述,核密度估计在拟合风光数据方面具有较好的适用性,对该地风电出力、光伏出力直接进行拟合,可避免拟合后数据转换造成的误差。该地光伏电站的额定功率为100MW,风电机组的额定功率为80MW。计算窗宽:风电数据总数1=8 760,标准差1=0.176,窗宽1=0.030 3;光伏数据总数2= 8 760,标准差2=0.291,窗宽2=0.050 2。
然后进行非参数核密度估计,并对拟合结果进行拟合优度与精度检验,结果见表4。其中,Pearson2的临界值为18.694,K-S的临界值为0.036 5。从表4可以看出,在对风电出力与光伏出力的数据进行拟合时,利用核密度估计法进行概率密度拟合,可满足拟合优度检验及拟合精度检验,风光的核密度估计具体表达式为
表4 基于核密度估计的风光出力拟合检验结果



式中,X为风光实际样本值。
基于五种Copula函数,分别建立风电场与光伏电站有功功率出力的预测误差联合分布函数,如图5、图6所示。

图5 椭圆族Copula的密度函数与分布函数

计算经验Copula累积分布函数,如图7所示。

图7 经验Copula分布函数
从图5~图7可以看出,Frank-Copula的分布函数与经验Copula的分布函数最为接近。
然后,依次计算各个Copula函数的Kendall秩相关系数、Spearman秩相关系数及每一种Copula与经验Copula函数的平方欧式距离,结果见表5。
表5 各Copula函数的相关系数与平方欧氏距离

从表5可以看出,使用Frank-Copula法计算得到的各相关系数与样本数据的相关系数较为接近,而且Frank-Copula与经验Copula的欧式距离在所有结果中是最小的。除此以外,Frank-Copula函数可以同时考虑变量的非负与负相关的关系,恰好风电出力与光伏出力互补、具有负相关的关系。虽然表5中t-Copula的相关系数也比较良好,但由于其与经验Copula的欧式距离过大,说明该类型Copula函数拟合效果不佳,因此不太适合将t-Copula作为最优拟合函数。综上所述,本文选取Frank- Copula进行数据拟合,从而保证了拟合的精度。
采用Frank-Copula函数进行拟合,利用极大似然估计法进行参数的估计,得=0.285。联合分布函数的表达式为
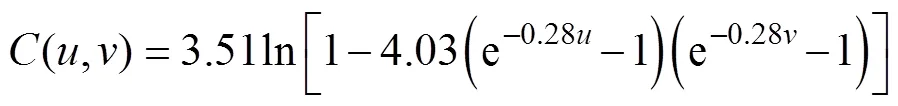
对24个时段风电出力数据与光伏出力数据分别进行Frank-Copula函数拟合,然后利用蒙特卡洛采样生成场景。
基于2.2节的场景生成方法,生成500个风光互补场景,然后利用后向缩减法分别对生成的大量风电与光伏场景进行缩减,并求出每个场景的概率,如图8、图9所示,图中的出力均为标幺值。缩减后各个场景的概率见表6。

图8 风电出力缩减场景

图9 光伏出力缩减场景
采用差异系数CV衡量所生成风电出力与光伏出力的互补特性,按照上述计算过程进行年度场景生成5次,得到5组年度数据,差异系数比较见表7。
表6 缩减后各场景的概率

表7 差异系数比较
4 结论
本文基于非参数核密度估计法,利用多种Copula函数建立风光联合时序出力模型,通过比较各秩相关系数与平方欧氏距离,选取最优Copula函数对各个时刻的风电出力数据与光伏出力数据进行拟合,得到每个时刻的考虑风光出力相关性的概率密度函数,利用Copula函数的蒙特卡洛采样方法生成年度场景。以江苏某地区年度风光实际出力数据为例,验证所提方法及模型,分析结果表明:
1)非参数核密度估计法较参数估计法能更好地拟合样本数据,所得模型更接近真实值。
2)所提基于最优Copula函数的蒙特卡洛采样方法能够生成具备互补特性的风、光年出力场景,可应用在电力系统规划模型中,能够为电力系统可靠性分析提供数据基础。
[1] HOICKA C E, ROWLANDS I H. Solar and wind resource complementarity: advancing options for renewable electricity integration in Ontario, Canada[J]. Renewable Energy, 2011, 36(1): 97-107.
[2] 乔延辉, 韩爽, 许彦平, 等. 基于天气分型的风光出力互补性分析方法[J]. 电力系统自动化, 2021, 45(2): 82-88.
[3] 白桦, 王正用, 李晨, 等. 面向电网侧、新能源侧及用户侧的储能容量配置方法研究[J]. 电气技术, 2021, 22(1): 8-13.
[4] 钟嘉庆, 李茂林, 江静, 等. 基于Copula理论的风/光出力预测误差分析方法的研究[J]. 电工电能新技术, 2017, 36(6): 39-46.
[5] 偲默, 苗世洪, 霍雪松, 等. 基于动态Copula的风光联合出力建模及动态相关性分析[J]. 电力系统保护与控制, 2019, 47(5): 35-42.
[6] HAGHI H V, BINA M T, GOLKAR M A, et al. Using copulas for analysis of large datasets in renewable distributed generation: PV and wind power integration in Iran[J]. Renewable Energy, 2010, 35(9): 1991-2000.
[7] 周泽人, 舒印彪, 董存, 等. 基于混合威布尔分布的风能资源分布统计分析研究[J]. 数理统计与管理, 2020, 39(4): 584-594.
[8] 赖昌伟, 黎静华, 陈博, 等. 光伏发电出力预测技术研究综述[J]. 电工技术学报, 2019, 34(6): 1201-1217.
[9] 李鹏. 电力需求响应机制下含电池储能系统的风光互补发电系统经济调度研究[J]. 电气技术, 2015, 16(3): 57-60.
[10] 白顺明, 陈磊, 姜飞, 等. 考虑风电最大化消纳的电力系统多目标优化[J]. 电气技术, 2020, 21(1): 7-11.
[11] 吴治均, 李明昆. 基于馈线路径集合法的并网型微电网可靠性评估[J]. 电气技术, 2016, 17(10): 17-22.
[12] 黎静华, 文劲宇, 程时杰, 等. 考虑多风电场出力Copula相关关系的场景生成方法[J]. 中国电机工程学报, 2013, 33(16): 30-36, 21.
[13] 杨楠, 黄禹, 叶迪, 等. 基于自适应多变量非参数核密度估计的多风电场出力相关性建模[J]. 中国电机工程学报, 2018, 38(13): 3805-3812.
[14] ARIK I, KANTAR Y M, USTA I. The new odd-Burr Rayleigh distribution for wind speed characterization[J]. Wind & Structures, 2019, 28(6): 369-380.
[15] 车兵, 李轩, 郑建勇, 等. 基于LHS与BR的风电出力场景分析研究[J]. 电力工程技术, 2020, 39(6): 213-219.
[16] 周博, 艾小猛, 方家琨, 等. 计及超分辨率风电出力不确定性的连续时间鲁棒机组组合[J]. 电工技术学报, 2021, 36(7): 1456-1467.
Typical scene generation of wind and photovoltaic power output based on kernel density estimation and Copula function
SONG Yu LI Han
(State Grid Jiangsu Electric Power Co., Ltd Maintenance Branch Company, Nanjing 211102)
The randomness, volatility and intermittent nature of new energy resources bring troubles to power system planning. A reasonable description of how wind power and photovoltaic output behave and generating typical output scene is a common method for new energy planning. A method for generating typical scene of relevant wind power and photovoltaic output is proposed. This paper firstly fits a large number of sample data based on kernel density estimation, and performs fitting and pre-test to obtain a kernel density estimation expression of wind and photovoltaic power output. This paper builds a variety of combined distribution models of wind and photovoltaic power based on Copula functions, and then judges the fitness of each model. The Kendall and Spearman correlation coefficients of each model are considered to select the optimal Copula function as wind power, photovoltaic joint probability distribution. Finally, the annual power output of wind and photovoltaic power is generated based on the optimal Copula joint probability distribution. Case analysis shows that the simulation results of annual output of wind and photovoltaic power meets their relevance, and has higher accuracy in wind and photovoltaic power output in the reaction. There must be a certain reference value for the reliability analysis of power system and grid planning.
kernel density estimation; Copula function; scene generation; complementary characteri- stics; difference coefficient
2021-08-30
2021-10-08
宋 宇(1989—),男,江苏省南通市人,硕士,工程师,主要从事继电保护及自动化相关工作。

