基于蒙特卡洛方法的可靠性灵敏度分析★

刘晓静

（山西工程职业学院，山西 太原 030009）

引言

可靠性灵敏度分析方法是基于可靠性计算方法之上的分析方法，是可靠性分析方法的递进。早在1985年HaftkaRT,GurdalZ[1]就对结构系统的敏感度设计进行了研究。张义民[2]等提出了单自由度非线性随机参数振动系统的可靠性灵敏度分析，讨论了随机参数服从正态分布的机械结构的可靠性灵敏度设计。

建立刚性四杆机构输出角的模型，采用蒙特卡洛方法对输出角的可靠性灵敏度进行研究，为后续有效提高运动机构的可靠性和稳健性打好基础。

1 Monte Carlo可靠性灵敏度

结构在规定时间和规定条件下完成规定功能的能力，称为可靠性[3]。在规定时间和规定条件下完成预定功能的概率为可靠度。可靠性对于基本随机参数的偏导数为可靠性灵敏度。

灵敏度为失效概率pf对基本变量xi的分布参数（i=1，2，…，n；k=1，2，…，m），其中mi为第i个变量xi分布参数总数的偏导数，将失效概率的积分对分布参数求导数，则得到可靠性灵敏度如下[4]：

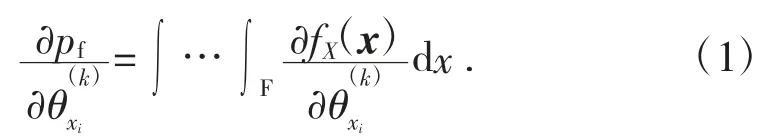
Monte Carlo[5]模拟过程中，采用样本均值代替总体均值，数学期望可以用样本函数的均值来估计：

失效概率对于参数的无量纲灵敏度系数表达式如下：

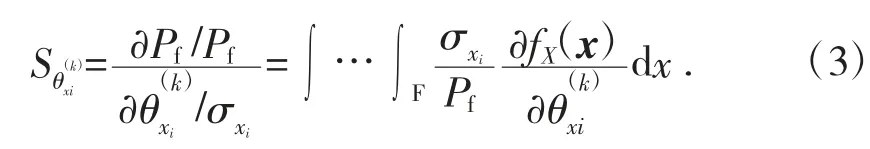
服从正态分布的变量的失效概率对于均值和标准差的无量纲灵敏度系数[6]如下：

式中，uji为第j个样本xj=（xj1，xj2，…，xjn）T的第i个分量对应的标准正态变量，即。

系统不能完成规定功能的概率表示为失效概率pf。系统的可靠度pr与失效概率满足以下关系式：

系统可靠性分析的主要问题就是处理系统的随机问题来确定系统的失效概率。

如果连续随机变量Z的概率密度函数为fZ（z），则由失效概率的意义可知：

如果用fX（x）=fX（x1，x2，…，xn）表示基本随机变量X=（X1，X2，…，Xn）T的联合概率密度函数，用FX（x）=FX（x1，x2，…，xn）表示联合累积分布函数，那么系统的失效概率可表示为：

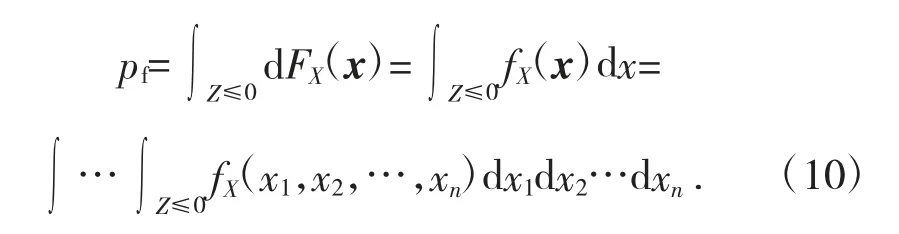
若各基本随机变量Xi之间相互独立，且Xi的概率密度函数为fX（ix）i，则失效概率为：

可靠指标是可靠性指标的简称[5]。由于基本随机变量的不确定性，其联合概率密度函数的获取比价困难，联合概率密度函数的计算也非常困难，因此在工程上一般不使用式（11）来计算失效概率。根据可靠性指标与失效概率的对应关系，通过计算可靠性指标来确定系统的可靠性。

假设功能函数Z~N（μZ，σZ），则功能函数的概率密度函数为：

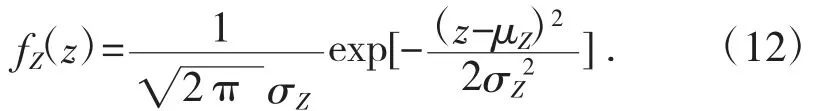
通过变换，Y=（Z-μZ）/σZ，可以将功能函数转换成标准正态分布Y~N（0，1），那么其概率密度函数和累积分布函数为：

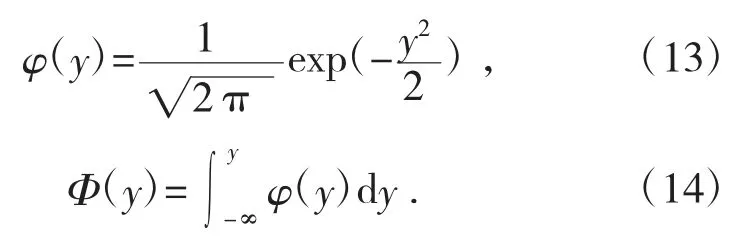
将式（6）代入式（4），并注意到式（7）和式（8），则失效概率[6]为：

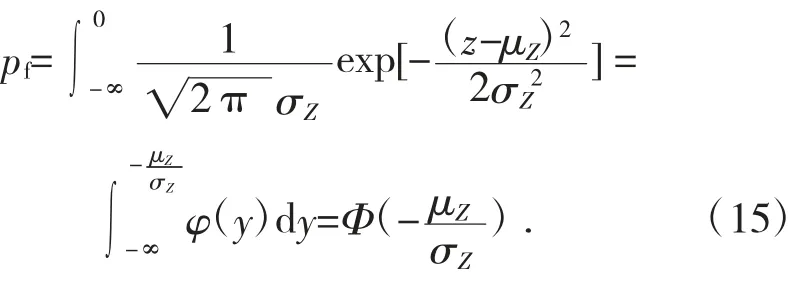
可靠性指标、失效概率和可靠概率就可以分别表示为：

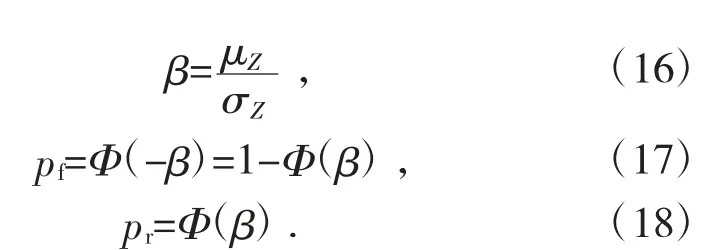
上述对可靠指标的计算是建立在功能函数服从正态分布的条件下。当pf≥0.001（或β≤3.090 2）时，失效概率的计算结果能够满足工程上所要求的精度，因此可以不考虑基本变量的分布类型而简化计算过程；当失效概率或可靠指标不满足以上关系时，必须考虑功能函数的概率分布形式。

Monte Carlo法计算求解齿轮接触疲劳可靠度的大致过程如下为：由基本随机参数的联合概率密度函数fX（X）模拟产生N组随机样本xj（j=1，2，…，N），把样本数据值代入齿轮接触疲劳的极限状态方程里，然后统计落入可靠域的样本点数，即齿轮传动齿面接触应力小于齿面许用接触应力Nr，用频率Nr/N近似代替可靠度PR，则

2 算例

图1为四杆

图1 四杆机构角度示意图

机构的角度示意图，主动杆件转速为300 r/min，L1，L2，L3，L4已知，具体值及分布类型见下表1。

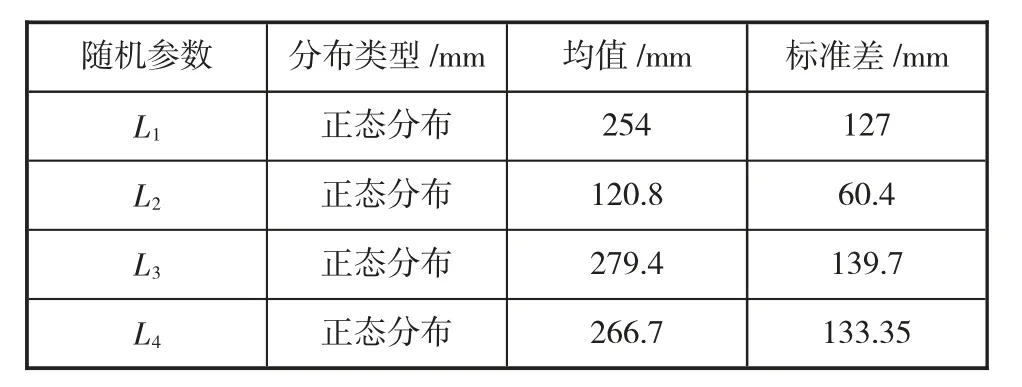
表1 弹性四杆机构的参数

下页图2为基于蒙特卡洛方法对四杆机构输出角可靠性分析流程图。

根据表1机构变量参数表对参数抽取106个样本点，计算刚性机构输出角并进行可靠性及灵敏度分析，根据式（5）和式（6）对输出角的失效概率关于各参数求均值与标准差灵敏度进行求解。

从下页图3、图4中可以看出，对于输出角的失效概率对于杆件L3的敏感度程度相对大。可以看出各参数的均值灵敏度有正值有负值，说明不同参数的均值对于输出角的失效概率影响有正有负。L3均值灵敏度均为正值，说明L3的均值对于失效概率的影响是积极的。而对于各参数的标准差灵敏度则基本为负值，各参数标准差对于失效概率的灵敏度影响是消极的，且L3的标准差对灵敏度消极影响较其他参数更大。

图3 均值灵敏度直方图

图4 标准差灵敏度直方图

3 结语

各参数均值中对输出角的影响最大的为L3，并且是积极影响；各参数的标准差对输出角的影响最大的也为L3，并且是消极影响。

由此通过计算可以得到弹性四杆机构中任意一点处，随着主动杆件转动，各参数对于输出角可靠性影响，为后续有效地提高运动机构的可靠性和稳健性打好基础。