基于空耦超声共振法的复合材料测厚技术研究

，，

(中北大学信息与通信工程学院，山西 太原 030051)

0 引言

碳纤维复合材料是高性能的结构材料，具有强度高、耐腐蚀、耐摩擦和应用范围广等优点，被应用在航空、航天和军事等工业领域[1]，其是将2种或2种以上的材料优化组合而成。复合材料在制造、加工和使用过程中会产生缺陷，严重影响材料结构性能[2]。因此，复合材料缺陷检测成为如今关注的焦点。利用超声测厚技术对复合材料进行检测，通过测量材料的厚度反推出缺陷的大小。超声测厚因其透射性强、无损伤、无害和成本低等优点，被应用于工业生产的很多方面[3]。根据工作原理的不同，超声测厚方法可分为3种：脉冲反射式、兰姆波式和共振式。脉冲反射法[4]检测薄件时相邻的回波发生混叠，其测量厚度的范围在1～1.5 mm。兰姆波法[5]产生条件相对复杂，对探头放置角度要求较高，部分技术问题尚未解决。共振法主要针对于超薄材料的厚度测量，一定程度上凭借连续高频率超声波激励系统[6]，通过测定材料的共振频率来计算材料的厚度，可测得材料的厚度在0.1 mm左右，对比分析可知，该方法可实现更高精度的测量，操作更为便捷。

本文通过COMSOL Multiphysics有限元仿真分析软件建立仿真模型，在复合材料内部置入不同大小空气层以模拟实际分层缺陷，换能器激发超声信号通过空气进入材料内部传播产生共振现象，分析谐振频率与厚度之间的关系，从而检测出复合材料中缺陷的厚度。验证超声共振法在实际检测中的可行性和实用性，并提供实质性的参考与借鉴。

1 空耦超声共振法检测原理

选用碳纤维复合材料进行实验，复合材料的分层缺陷主要出现在材料内部，三维分层缺陷如图1所示。

图1 复合材料分层缺陷

本文使用COMSOL有限元仿真软件将非接触式空气耦合超声共振检测技术应用在复合材料的缺陷厚度检测中，空耦超声共振法检测原理如图2所示。

图2 空耦超声共振法检测原理

当频率可变的连续波垂直进入被测物体内传播时，在材料上下界面发生多次反射，遇到缺陷时发生反射、透射和折射等行为。当被测物体的厚度等于半波长的整数倍时，多数入射波与反射波相互叠加形成驻波[7]，在被检测物体内传播的超声波频率和固有频率相等时形成共振[8]，依据该频率可计算出物体的厚度，其关系式为

(1)

f1,f2,f3,…,fn为一阶谐振频率，二阶谐振频率，三阶谐振频率，…，n阶谐振频率。当知道任意2个相邻谐波共振频率之后，利用速度与谐振频率之间的关系可得到厚度为

(2)

通过理论分析推算出

(3)

c为被检测材料的声速；f为声波谐振频率；δ为待测物体的厚度；n为半波长的倍数；λ为超声波的波长。

2 模型建立与分析

2.1 几何建模

运用固体力学(弹性波)、AC/DC(静电、电路)模块多物理场耦合，选择瞬态分析模式。空耦超声换能器进入空气到达复合材料的二维模型如图3所示。空气域左右两侧及下侧设为完美匹配层(PML)，上表面为辐射边界，复合材料的左右侧设为低反射边界条件，超声压电换能器耦合电路场形成谐振电路。设置全局探针接收超声信号。

图3 复合材料脱粘检测二维结构模型

设置碳纤维复合材料板宽为100 mm，高为5 mm，超声换能器应根据被测物体的尺寸、材料和缺陷大小等因素进行选择，若工作频率过高则会导致超声波信号在空气或材料中衰减过快而无法到达被测物体底面；若频率过低则遇到缺陷时声波绕射，无法检测出缺陷大小，导致检测精度不高。初步选择中心频率为800 kHz的空耦超声换能器，宽为20 mm，高为3 mm。

在谐振工作状态下，压电体由于逆压电效应产生激烈振动，在振动过程中克服内摩擦而产生机械损耗[9]，为了提高电声与声电之间的耦合度，应选择机械品质因数较低的压电材料，故本文选用PZT-5H压电晶片作为换能器仿真材料。由于声场的强度、声束的宽度分别影响着穿透能力和横向分辨率，声波在近场区声压起伏密集，对测量的影响较大，因此在超声厚度测量中选择远场区进行分析，图4为800 kHz聚焦换能器声场分布，从而确定换能器与被测物体之间的最佳检测距离为40 mm。

图4 800 kHz聚焦换能器声场分布

2.2 网格和时间设置

求解结果前，需对模型进行网格划分，超声波在物体内传播呈现出不同扩散方向，较大的网络单元间隔会导致信号传播失真，网格越小计算越准确，但是网格过小会影响检测精度。考虑到计算机的计算能力，在对模型数据后处理时，为提高计算精度，选择每个波长包含12个单元间隔[10]，网格尺寸方程为

(4)

θ为最大单元网格尺寸；λmin为声波成分中最短的波长。为提高计算的准确性，保证计算结果收敛，有限元步长时间Δt需满足

(5)

vmax为最大声速，可得时间步长为0.1 μs。

2.3 压电换能器激励信号

根据超声共振法原理，利用线性调频信号(也称为Chirp信号)激励换能器发射和接收超声信号。线性调频信号具抗噪声干扰能力强和目标缺陷分辨能力高的特性[11]，可提高时间和距离分辨率。线性调频信号的时域数学表达式为

s(t)=Acos(2πf0t+πkt2+φ0)

(6)

调频信号的调制斜率为

(7)

信号的瞬时频率为

(8)

其中，幅度A=100；信号持续时间T=150 μs；φ0为初始相位；f0为起始频率；频率扫描范围为200 kHz～5 MHz；中心频率为f=800kHz。在超声共振测厚系统中，压电超声换能器将电信号转换成超声波信号，实现电能和机械能的相互转换，当电源频率满足一定的条件时，电路发生谐振，回路中的振荡幅度达到最大值[12]，通过电路分析，调节电容C使电路发生谐振。

3 实验结果及误差分析

3.1 不同厚度复合材料板仿真实验

分别对1.00 mm、2.00 mm、3.00 mm、4.00 mm和5.00 mm厚的复合板进行仿真，图5a～图5e是厚度为1～5 mm的频谱分布图，表示谐振频率变化情况。从图5中可以看出，不同厚度薄板的仿真频域波形幅值不同，随着厚度的增大，信号幅值减小。

将仿真所得实验结果一阶谐振频率与根据检测物体的实际厚度计算出的基本谐振频率进行对比，发现两者相近，证明实验结果的正确性。根据厚度公式(2)可计算出铝板的厚度。表1为不同厚度铝板的一阶、二阶谐振频率的变化及厚度测量结果的误差分析，从结果来看，相对误差范围均分布在5%以内，从而验证超声共振法在复合材料厚度检测中的可行性。

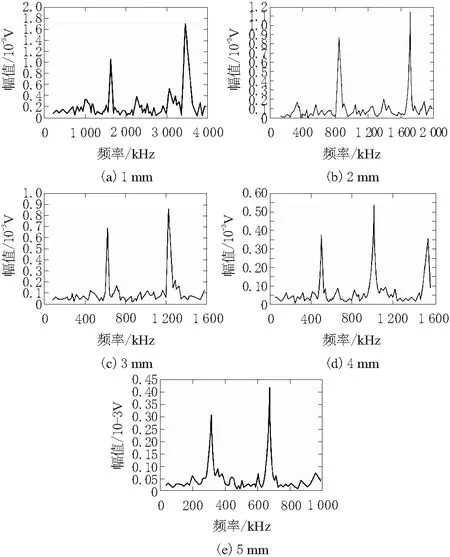
图5 不同厚度复合板频谱分布

表1 不同厚度复合板谐振频率变化及测量结果误差分析

3.2 不同缺陷复合材料板仿真实验

在实际工程中，由于制造和使用中的人为因素，使得板材内部会出现不同程度的分层缺陷。本文选择100 mm×1 mm的复合板进行仿真实验，在其中分别设置厚度为0.1 mm、0.2 mm和0.3 mm,宽均为20 mm的矩形缺陷进行对比实验，选择中心频率为2 MHz的换能器。

图6为不同大小矩形缺陷频谱图，存在缺陷时所显示的频谱图分布杂乱。图6a为0.1 mm缺陷，其一阶谐振频率为2.13 MHz，二阶谐振频率为4.16 MHz，根据共振法厚度计算式(2)可得厚度为0.86 mm，则缺陷大小为0.14 mm，与实际值相差0.04 mm，相对误差为4.44%。图6b为0.2 mm缺陷，通过提取一阶、二阶谐振频率2.39 MHz、4.65 MHz，计算所得复合板厚度为0.77 mm，则缺陷大小为0.23 mm，与实际值相差0.03 mm，相对误差为4.12%。图6c为0.3 mm缺陷，通过提取一阶、二阶谐振频率2.59 MHz、5.15 MHz，计算所得复合板厚度为0.68 mm，则缺陷大小为0.32 mm，与实际值相差0.02 mm，相对误差为2.85%。出现误差原因一方面是缺陷边缘形状，另一方面是仿真值与理想值的偏差。通过以上实验可以得出复合材料薄板缺陷的大小，从而体现出复合材料内部分层缺陷的严重程度。

图6 不同大小矩形缺陷频谱

4 结束语

为了检测复合材料薄件的厚度以及其中存在微小缺陷的大小，本文使用超声共振法测厚技术对不同厚度、含不同缺陷大小的复合板进行了仿真实验，利用有限元软件分析了声波进入材料产生共振，对产生的瞬态回波信号进行快速傅里叶变换，通过超声共振法的理论，计算出铝板的厚度，从而推导铝板缺陷大小。结果表明，超声共振法对缺陷大小进行定性、定量检测；不同缺陷大小所对应的频谱分布不同，厚度越薄处对应的谐振频率越高，检测精度可达0.1 mm左右，相对误差范围均分布在5%以下。空耦超声共振法解决了耦合剂污染被测物体、检测精度低和效率低等问题。对超声共振法提供了新的检测方向，为之后研究不同类型缺陷的材料打下基础。