含滑动节点索结构体系分析方法研究*

刘学武，李 博，侯亚委，李庆建

(华电重工股份有限公司，北京 100070)

0 引言

索在结构工程中扮演着非常重要的角色，如索道、悬索结构和斜拉结构等中拉索均为非常活跃的单元[1]。拉索连接节点在工程应用中可分为2种形式：①不滑动节点，即索与索或索与构件之间的连接为“死结”，不会产生相对滑移，如索网结构和索杆结构等节点；②索在节点处可产生相对滑移，如索道中跑车滑轮与索之间可产生相对滑移。含滑动节点索结构体系的受力特点为：由某一初始位形释放结构体系，结构体系在不平衡力系作用下最终达到平衡状态及几何姿态，且有时会伴有一定的结构位移，受力具有双重非线性，即索非线性及节点滑动接触的非线性，受力分析较复杂，难以精确模拟。

不滑动索系结构的分析相对简单，国内外很多学者对索单元进行研究，但对含滑动节点索结构体系模拟分析方法的研究相对较少。若采用现有有限元软件中的接触算法可得到有效求解，但非常繁琐。文献[2]提出一种有效的滑移索单元法，但需求解复杂的滑移刚度矩阵；文献[3]建立了一种考虑索滑移算法，但在求解各索段原长时采用了不考虑弹性的索长计算公式；文献[4]建立了调整支点两侧索力的方法，但增加了滑移处索长的调整；文献[5]提出了在中间节点处可自由滑动的多跨连续索静力平衡的算法；文献[1]通过虚加温度荷载方法来调整滑轮两侧索段原长，使两侧索力相等，但在求解多滑轮组问题时算法收敛困难；文献[6]提出一种三节点摩擦滑移索单元；文献[7]在处理荷载缓和体系时，提出了能量搜索法和动力松弛法，但只能处理索端张力已知的问题。

然而，上述方法并不能考虑在可滑动支座处，滑轮或鞍座半径对索受力状态的影响。Mcdonald等[8]借助索和滑轮相互作用中的4个独立内变量建立了一种单元，可模拟索在由1个链杆连接的滑轮上的滑动。借鉴该方法，魏建东[9]建立了索在滑轮上滑动模拟的滑移索单元，同时魏建东等[10]建立了滑轮在索上行走分析的索-滑轮单元。本文将上述单元统称为滑移索单元，其求解方法与常规有限元法相同，便于应用。本文进一步对滑移索单元进行探讨，构建滑移索单元高效求解的延拓牛顿法，给出索结构体系精确分析方法，编制相应的有限元分析程序，为实际工程的设计和施工提供可靠分析手段。

1 滑移索单元

滑移索单元[8-10]为一个平面三节点单元，3个节点分别为索两端点I(xI,yI)，J(xJ,yJ)及滑轮中心点K(xK,yK)，每个节点有2个自由度ux，uy，相应节点力分别为Fx，Fy。索采用悬链线模型，索和滑轮之间可产生相互滑移，设3个节点的坐标、位移和力列阵分别为Xe，ue和Fe。

滑移索单元在给定节点I，J之间索原长的情况下，利用4个内变量V1～V4即可确定其几何形状，设其组成内变量矢量Ve。

对于滑移索单元，通过直接建立节点力和位移的增量方程来推导单元刚度矩阵较困难。文献[8-10]通过内变量建立单元节点力和位移之间的关系，进而可获得单元刚度矩阵，推导基本过程如下。

1)选择单元内变量Ve。

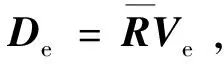
4)联立单元节点力和位移分别与内变量之间的增量方程，得到单元增量控制方程ΔFe=KeΔue及切线刚度矩阵Ke=MN。

实际工程索结构中存在的滑动节点及其对应的滑移索单元类型可分为3种：①滑移索单元Ⅰ型 索悬挂在滑轮上；②滑移索单元Ⅱ型 滑轮在索上行走；③滑移索单元Ⅲ型 索与滑轮在侧面接触。

滑移索单元Ⅰ型内变量和节点力分别如图1，2所示。滑移索单元Ⅰ型4个内变量的物理意义分别为[8-10]：V1为左索段在滑轮脱离点A处的张力，V2为从竖直方向逆时针绕滑轮中心点K旋转到左索段脱离点A的角度，V3为从竖直方向顺时针绕滑轮中心点K旋转到右索段脱离点B的角度，V4为左索段节点I，A之间无应力原长。这些内变量的选择不是唯一的，但利用其推导的公式形式最为简单。

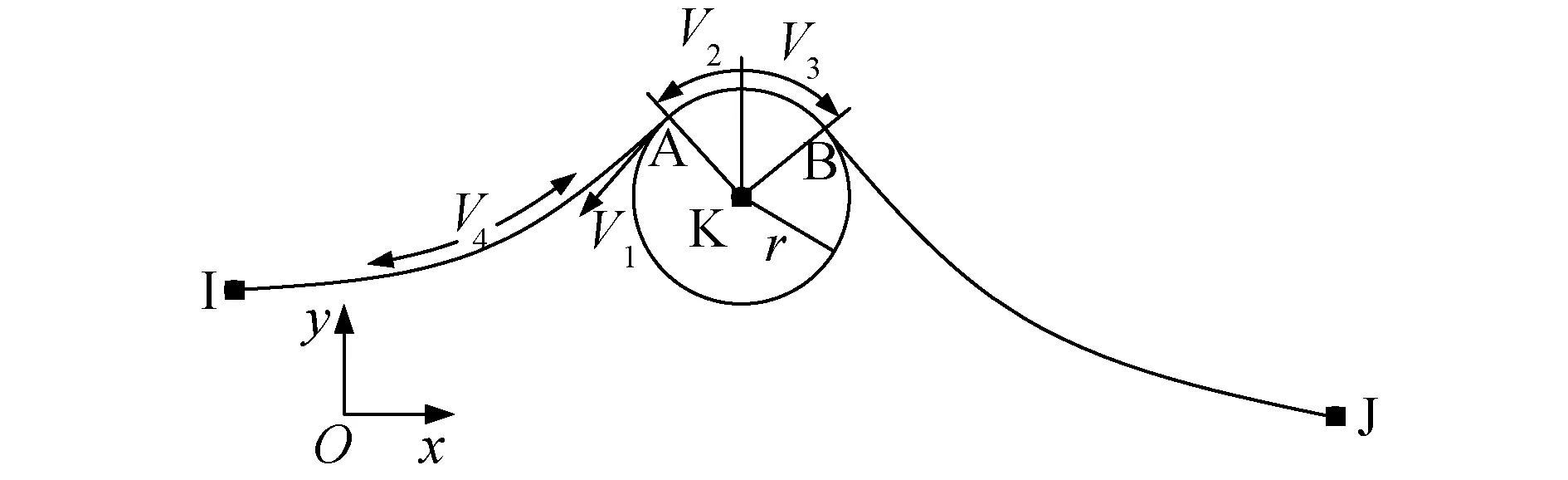
图1 滑移索单元Ⅰ型内变量

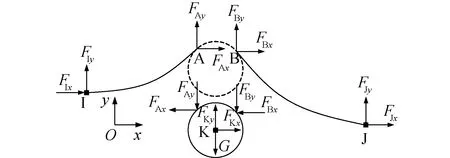
图2 滑移索单元Ⅰ型节点力

滑移索单元Ⅱ型内变量和节点力分别如图3，4所示。滑移索单元Ⅱ型4个内变量物理意义分别为[8-10]：V1为左索段在滑轮脱离点A处的张力；V2为从竖直方向顺时针绕滑轮中心点K旋转到左索段脱离点A的角度，V3为从竖直方向逆时针绕滑轮中心点K旋转到右索段脱离点B的角度，V4为左索段节点I，A之间无应力原长。

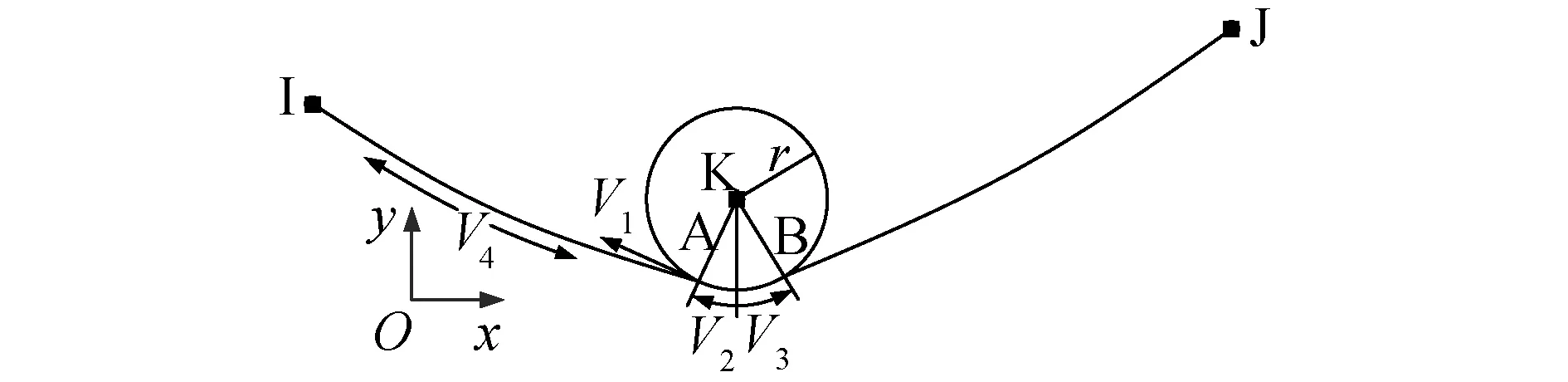
图3 滑移索单元Ⅱ型内变量

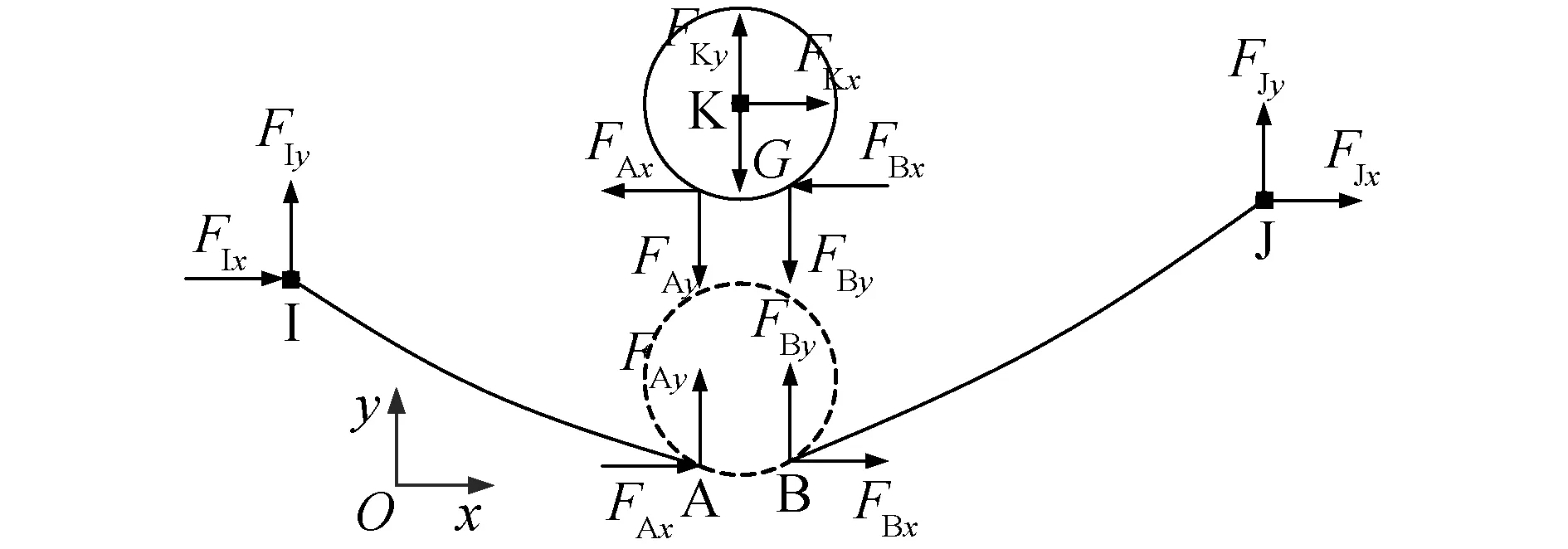
图4 滑移索单元Ⅱ型节点力

滑移索单元Ⅲ型内变量如图5所示。滑移索单元Ⅲ型4个内变量的物理意义分别为[8-10]：V1为下索段在滑轮脱离点A处的张力，V2为从水平方向顺时针绕滑轮中心点K旋转到下索段脱离点A的角度，V3为从水平方向逆时针绕滑轮中心点K旋转到上索段脱离点B的角度，V4为下索段节点I，A之间无应力原长。

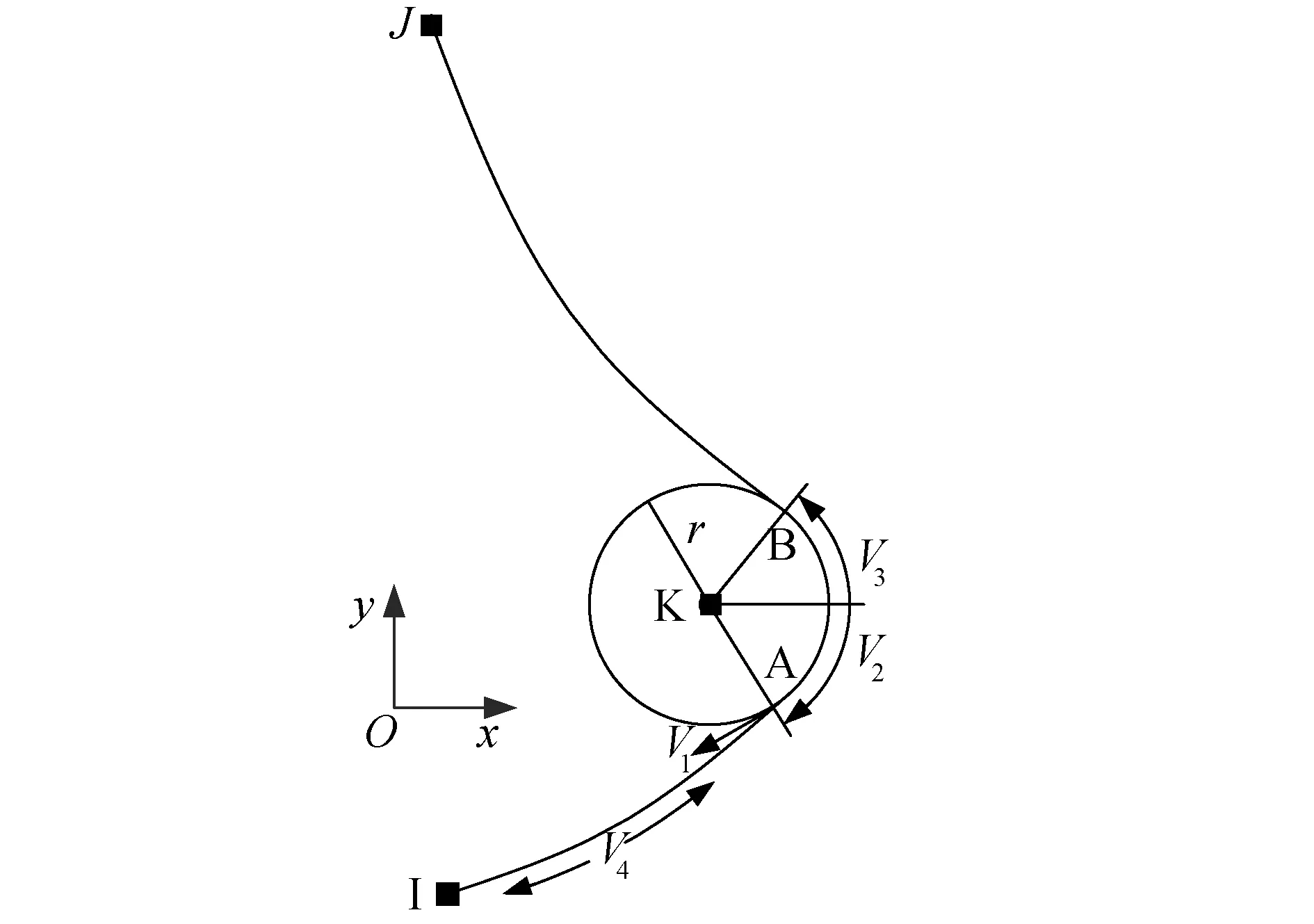
图5 滑移索单元Ⅲ型内变量

3类单元异同如下。

1)不同点 ①描述的物理现象不同，其中滑移索单元Ⅰ型描述的是索在滑轮上的滑移，滑移索单元Ⅱ型描述的是滑轮在索上的行走，滑移索单元Ⅲ型描述的是索在滑轮一侧滑移；②三类单元中表述内变量的坐标系不同。

2)相同点 ①单元构成相同，都是由1个滑轮和1段索组成；②单元受力机理相同，都是描述了索与滑轮之间的相互摩擦滑移；③从数学计算上来说，3类单元相同，具有通用性。

以下对3类单元通用性进行研究。取1段索悬挂在1个滑轮上的简单结构体系(见图1)，索两端和滑轮中心点固定，3个节点分别为I(-22，0)，J(22，0)，K(0，15)。索原长Lu=53.15m，截面面积A=2.0×10-4m2，弹性模量E=2.0×1011N/m2，索重w=50N/m；滑轮重G=0，半径r=0，摩擦效率e=1.0。采用3类单元确定体系平衡状态，结果如表1所示。

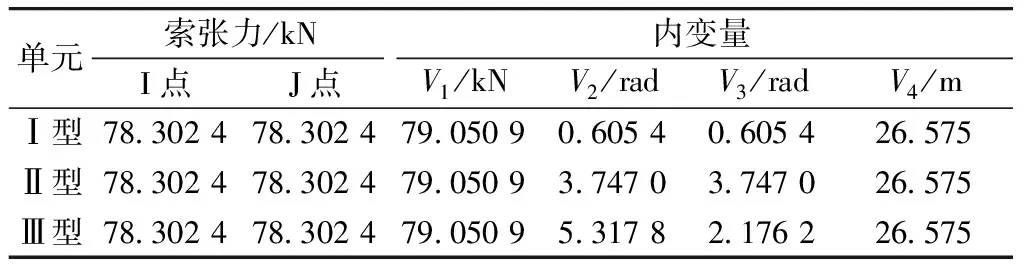
表1 3类单元索受力状态

通过算例可发现，3类单元分别求解同一个结构得到索的受力状态一致，只是单元内变量结果不同，这是由3类单元各自内变量坐标系不同而导致的，说明这3类单元具有通用性。因此，在对索滑动节点进行模拟时可采用其中任意一种单元，只是迭代初值的选择要与相应单元类型内变量的坐标系相对应。

2 单元求解方法

基于有限单元法，滑移索单元刚度矩阵和节点力的求解方法为：

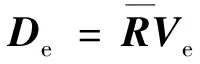
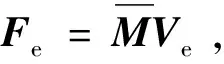
3)由Ve可得到单元刚度矩阵Ke。

由于牛顿法局部收敛，只有初值与精确值足够接近时才会迭代收敛。研究发现，内变量求解时其初值的选择须谨慎，直接影响解的收敛性。为扩大初值选择范围，构造了内变量求解的延拓牛顿法，基本思想为：先利用延拓法近似求解1个内变量，以此作为牛顿法的迭代初值进行求解，最终获得收敛解。

延拓牛顿法[11]基本思想为：引入参数t，构造1组映射H(x，t)代替单映射F(x)，使得H满足条件：

H(x0,0)=0，H(x,1)=F(x)

(1)

即当t=0时，H(x0,0)=0的解x0已知；当t=1时，H(x,1)=F(x)=0的解x*即为方程的解。满足上述条件常用的同伦为：

H(x,t)=F(x)+(t-1)F(x0)

(2)

延拓法迭代求解公式为：

其中，k=1,2,3，…,N-1。

牛顿法迭代求解公式为：

xk+1=xk-F′(xk)-1F(xk)

(4)

其中，k=N,N+1,N+2,…。

联立式(3)，(4)即为延拓牛顿法。其中，前面N步(式(3))主要是为求解x*的1个足够好的初始近似值xN，然后再用牛顿法(式(4))即可求得x更精确的近似解。

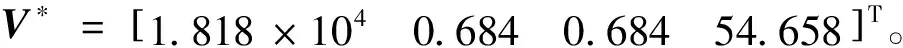
取不同迭代初值时牛顿法和延拓牛顿法收敛性如表2所示。其中，在采用延拓牛顿法时N取30，表中延拓牛顿法的迭代次数与牛顿法的迭代次数相同。

表2 迭代初值不同时牛顿法和延拓牛顿法的计算结果

从表2对单元Ⅰ型的算例研究可看出，采用牛顿法求解滑移索单元内变量时，存在一定的局部收敛性，算法不易收敛，而采用延拓牛顿法时具有较强的稳定性和收敛性，且迭代初值选择的范围较大。单元 Ⅱ，Ⅲ型的收敛性研究结果与单元Ⅰ型的收敛情况一致，在此不再赘述。

3 索结构分析方法

基于滑移索单元，可构建含滑动节点索结构体系精确模拟分析方法，其求解过程和步骤如下。

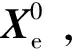
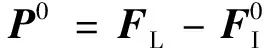
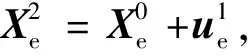
5)重复步骤4)，直至误差‖ΔPn‖≤ε和‖Δun‖≤ε，其中ε为小数，则求解收敛，即可得到整体结构受力状态。

6)求解过程中，若整体结构中存在梁、杆和壳等其他单元，其计算原理可参见相关文献，在此不再赘述。

上述方法建立的索结构分析程序在求解时需给出索原长，但在实际工程施工和设计中往往只给出预应力状态下索在控制点的张力或垂度限值，而索原长未知。因此，在对索结构进行分析时需首先假定索原长，然后以指定点的张力和垂度为目标变量进行迭代求解。

4 工程算例分析

采用上述方法编制了可精确模拟含滑动节点索结构体系分析的有限元程序，用于实际工程中该类结构设计和施工过程分析。

1)索道受力状态分析 取图6所示滑动索道体系，其中索两端点A，D固定，2个滑轮中心点B，C固定，索在滑轮上可滑移。索截面面积A=2.0×10-4m2，弹性模量E=1.9×1011N/m2，索重w=50N/m；滑轮重G=0，半径r=0.3m，摩擦效率e=1.0。E点作用1个竖向荷载P，分为P=0，P=5kN 2种情况进行讨论。将整个结构划分为2个索轮单元Ⅰ型进行求解，分析中首先给定索结构初始状态，即首先给出E点初始坐标及索原长。

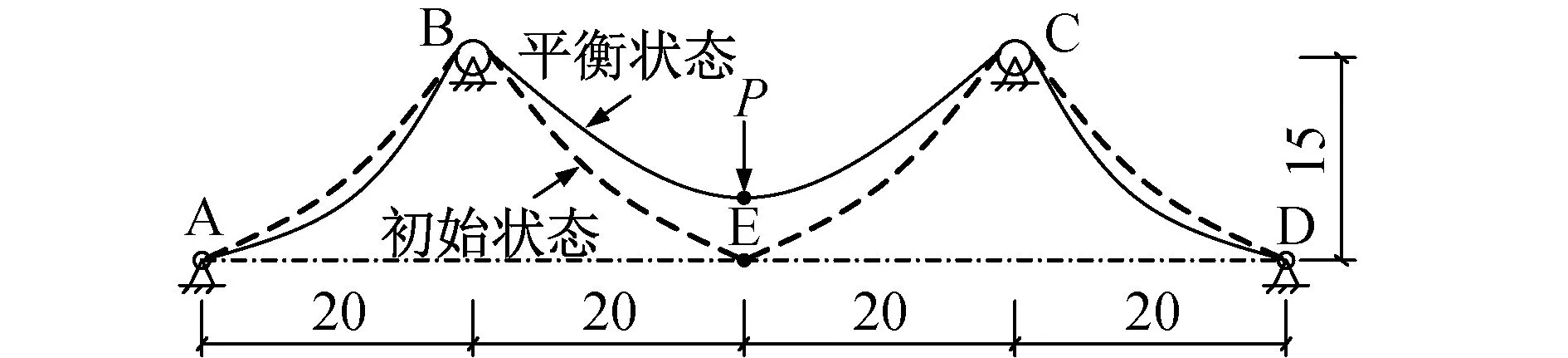
图6 滑动索道体系(单位：m)

分3种工况进行求解：①索原长为100m时结构的平衡状态；②索在A点张力为800N(P=0)和5kN(P=5kN)时索原长；③索跨中节点E垂度为10m(P=0)和13m(P=5kN)时索原长。各种工况下的求解结果如表3，4所示。在此设P为索道上跑车自重，则在给定索总原长的基础上改变其作用点E的位置，即可模拟固结式跑车在索道上的行走。对于轮式跑车，可在跑车作用处设置1个滑移索单元，跑车自重作用在滑轮上，同时增加1道牵引索，一端与跑车的滑轮中心相连，另一端连在牵引装置上，拉动牵引索改变跑车滑轮在索道上的位置，即可模拟跑车在索道上的行走。

表3 3种工况下的求解结果(P=0)

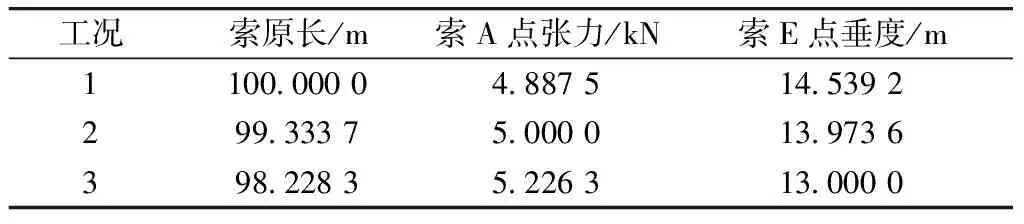
表4 3种工况下的求解结果(P=5kN)

2)悬索桥主缆受力状态分析 取图7所示悬索桥主缆进行分析，其中，缆索截面面积A=0.3m2，弹性模量E=1.9×1011N/m2，索重w=50kN/m；B，C处鞍座重G=0，半径r=0.5m，假设缆索与鞍座之间可产生相互滑移，摩擦效率e=1.0。取桥塔刚度足够大，不考虑加劲梁作用。分析中首先给定缆索初始状态，即首先给出E点初始坐标及缆索原长。分3种工况进行求解：①缆索原长为1 500m 时结构平衡状态；②缆索在A点张力为4.5×104kN时索原长；③缆索跨中节点E垂度为80m时索原长。求解结果如表5所示。分析中若将主缆根据设计分成若干索段，按施工方案依次安装吊索及加劲梁，即可模拟悬索桥在施工过程中的受力状态。

图7 悬索桥主缆(单位：m)

表5 3种工况下的求解结果

3)大跨度悬挑索-滑轮结构受力状态分析 取图8所示索-滑轮体系进行分析，其中索截面面积Ac=2.0×10-4m2，弹性模量Ec=1.9×1011N/m2，索重w=50N/m；滑轮半径r=0.3m，摩擦效率e=1.0。横梁截面面积A=1.466×10-2m2，惯性矩I=1.059 3×10-3m4，弹性模量E=2.06×1011N/m2。荷载P=10kN，不考虑横梁自重。分2种工况进行求解：①索原长为65m时结构平衡状态；②索在B点张力为18kN时索原长。2种工况下索和横梁受力状态如表6，7所示。

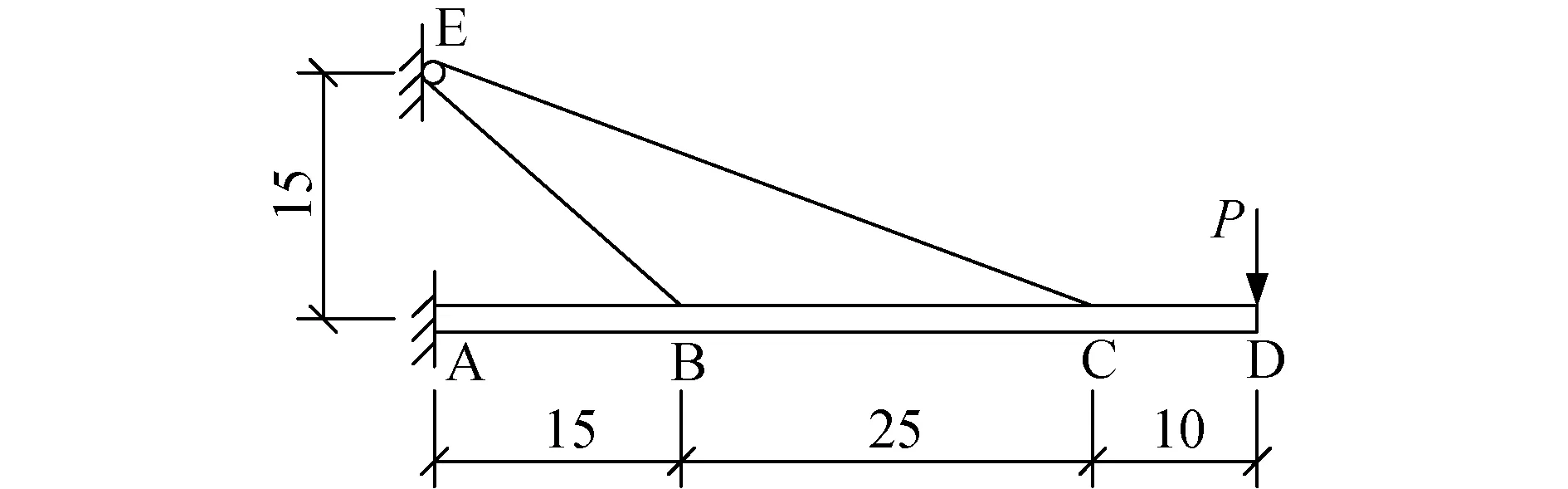
图8 大跨度悬挑索-滑轮结构体系(单位：m)

表6 2种工况下索受力状态

表7 2种工况下横梁受力状态

5 结语

1)对可精确模拟索结构中滑动节点受力特性的滑移索单元进行探讨，研究表明这3类单元也具有通用性。

2)构建了滑移索单元内变量求解的延拓牛顿法，能有效提高单元求解的收敛性，并且迭代初值选择范围更大。

3)构建含滑动节点索结构体系求解的迭代分析法，编制相应的有限元程序，算例分析表明，分析方法和分析程序正确，可用于实际工程的设计和施工分析。