M1 transition energy and rate in the ground configuration of Ag-like ions with 62 ≤Z ≤94

Ju Meng(孟举) Wen-Xian Li(李文显) Ji-Guang Li(李冀光) Ze-Qing Wu(吴泽清)Jun Yan(颜君) Yong Wu(吴勇) and Jian-Guo Wang(王建国)

1National Key Laboratory of Computational Physics,Institute of Applied Physics and Computational Mathematics,Beijing 100088,China

2Key Laboratory of Solar Activity,National Astronomical Observatories,Chinese Academy of Sciences,Beijing 100012,China

3HEDPS,Center for Applied Physics and Technology,and College of Engineering,Peking University,Beijing 100871,China

Keywords: Ag-like ions,magnetic dipole transition,fine-structure splitting

1. Introduction

Tungsten (W) is selected as a plasma-facing material for the International Thermonuclear Experimental Reactor(ITER),a magnetic confinement fusion device,because of its favorable physical, chemical and thermal properties, that is,the high energy threshold of sputtering, low sputtering yield,high re-deposition efficiency, and low tritium retention.[1-4]The W ions including Ag-like W27+, however, cause power loss by radiative emission and then may quench the fusion reactions, if entering into the edge region of plasma.[5]Therefore,the spectroscopic diagnostics of these W ions are critical for the operation of the fusion plasmas. On the other hand,accurate atomic data of these W ions are also essential to acquire the state of the fusion plasma such as electron densities and temperatures. Moreover, Ag-like ions, e.g., Nd13+and Sm15+,have been proposed as candidates for the development of the next generation atomic clocks due to their long-lived metastable states,transition wavelengths in optical range,and sensitivity to variation of the fine-structure constant.[6-8]In addition,theoretical investigation on the simple ground states of Ag-like ions can also be useful to test the quantum electrodynamics(QED)effects.

Measurements and theoretical calculations have been performed on the magnetic dipole (M1) transition energies and rates in the ground configuration 4d104f of Ag-like ions.Sugar and Kaufman[9]obtained the excitation energies of Ag-like ions(Z=58-67,74)with a high-voltage-triggered spark and photographed on the NBS 10.7 m grazing incidence spectrograph in the early 1980s. Over the past decades, most of the experiments were carried out by using the electron beam ion traps (EBITs), through which one could directly measure the fine-structure splittings in the ground configuration. For instance, Feiet al.[10]observed the M1 transition of Ag-like W (Z=74) using the Shanghai permanent magnet electron beam ion trap (SH-PermEBIT). Subsequently, Zhaoet al.[11]reported the wavelength for the M1 transition of Ag-like Yb(Z=70)with the same experimental facility. Murataet al.[12]identified the M1 lines of Ag-like Ho (Z=67), Er (Z=68)and Tm (Z= 69) ions by employing the compact electron beam ion trap (CoBIT) in Tokyo-EBIT laboratory.[13]In theory, Safronovaet al.[14]calculated the fine-structure splitting of the 4f2Foterm for certain Ag-like ions at the neutral end using the relativistic many-body perturbation theory(RMBPT).Ivanova[15,16]reported the energy separations in Ag-like ions with 50≤Z ≤86 based on the relativistic perturbation theory with a model potential(RPTMP).In the framework of the multi-configuration Dirac-Hartree-Fock (MCDHF) method,Dinget al.[17]gave the M1 transition energies along the Aglike isoelectronic sequence, in which only the core-valence(CV) correlation related to electrons in the 4d core subshell was included. Subsequently,Grumeret al.[18]reevaluated the wavelengths and calculated the corresponding transition rates in Ag-like ions with 50≤Z ≤94 based on the large-scale multiconfiguration Dirac-Hartee-Fock(MCDHF)calculations.In particular, they considered the effect of the CV correlation withn=4 andn=3 shells and pointed out the importance of these deep-core-valence correlations. Besides the systematic calculations for Ag-like ions along the isoelectronic sequence, there are also some investigations for a few individual ions.[6-8,19,20]Dzubaet al.[8]and Safronovaet al.[6,7]used the correlation potential method and the relativistic linearized coupled-cluster method with inclusion of all single, double,and partial triple excitations(SDpT),respectively,to obtain the transition energies for Ag-like Nd13+and Sm15+.Safronovaet al.[19,20]also made a detailed study on the atomic parameters of Ag-like W(Z=74)ion employing the RMBPT method.

As mentioned above, the calculated M1 transition energies in the ground configuration of Ag-like ions are mainly obtained with the MCDHF and RMBPT methods. These two methods are based on different theoretical approximations,that is, the variational principle and perturbation theory, respectively. Comparison of these two results can provide a reliable evaluation of accuracy for the atomic data of Ag-like ions. However, the difference in the fine-structure splittings is obvious for the low-Zions between the MCDHF[18]and the RMBPT[14]calculations,although the agreement becomes better at the high-Zend of the sequence. Therefore,it is necessary to carry out a new calculation,especially for the low-Zions in the Ag-like isoelectronic sequence, to provide more reliable and accurate atomic data.

In the present work,we have performed systematic calculations on the M1 transition energies and rates in the ground configuration 4d104f of Ag-like ions betweenZ=62 and 94 using the second-order RMBPT implemented in the Flexible Atomic Code(FAC).[21]In order to evaluate the reliability of the present RMBPT results,extensive comparisons have been made with the available experimental data,as well as with the previous theoretical results. The data in the present work is useful for the spectral simulation and plasma diagnostics.

2. Theoretical method

In the present work,the second-order RMBPT is adopted to perform the calculations. This method was implemented within the FAC package by Gu[22-25]and has been widely used in atomic structure calculations. The details of the RMBPT method can be found elsewhere.[26-30]Here, we only give a brief description.

The Hamiltonian of a many-electron atomic system withNelectrons is written in the Dirac-Coulomb-Breit (DCB)approximation[31]as

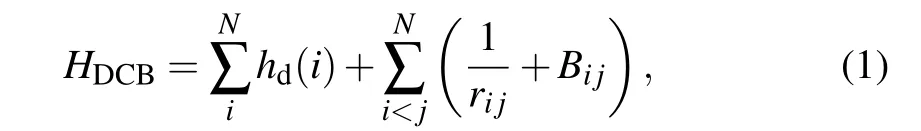
wherehd(i)is the one-electron Dirac Hamiltonian in which the electron kinetic energy,the resting energy,and the coulomb interaction between electrons and the nuclei are included,Bijis the frequency-independent Breit interaction,

From Eq.(6),we know that the eigenvalues and eigenfunctions ofHeffare the exact energies and the model functions,respectively. This means that the true energies of the system can be obtained by solving the eigenvalue problem of an effective HamiltonianHeffin the model spaceM. The wave operatorΩsatisfies the operator relation

in terms of matrix elements in the model spaceM.

By solving Eq.(6),we can obtain the total energy of the system as follows:

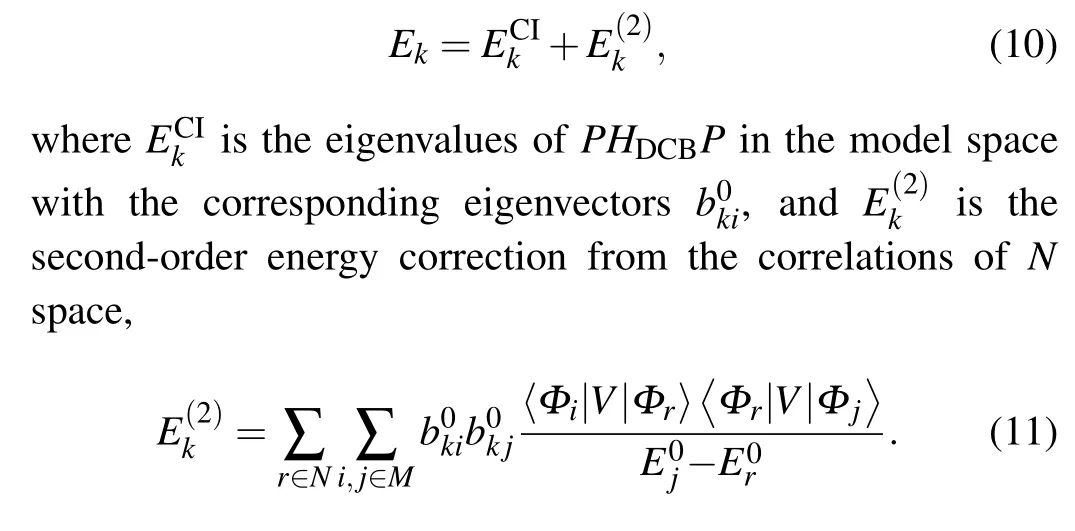
The Dirac-Fock-Slater approximation is employed to produce the function basis{Φr}. This means that the central potentialU(r)in Eq.(3)is a modified Dirac-Fock-Slater potential including the spherically averaged potential due to bound electrons, and the local approximations to the exchange interactions excluding the self-interaction term. Furthermore, one-electron radial orbitals can be obtained by the self-consistent field procedures.

In the present work, theMspace includes the states belonging to 4d104f, while theNspace consists of all possible configurations generated by single and double excitation from each occupied orbital of the configurations in theMspace.For one-electron excitation, the maximum principal quantum numbernvalues is set to 170, and for double excitation, the maximumnvalues to 65. In addition, the maximum orbital angular quantum number is set tol=30. The extrapolation beyond the maximumnvalues is carried out for building the effective Hamiltonian. In addition, several small higher order QED effects are also taken into account in the present calculations, including the vacuum polarization and self-energy.In order to evaluate the accuracy of our calculations, we also investigated the convergence of atomic parameters concerned by increasing theNspace as discussed in Ref. [30]. For example,we performed an additional calculation for Ag-like Sm(Z=62)and Ag-like Eu(Z=63),in which we set the maximalnvalues for single and double excitations up to be 225 and 80,respectively. We found a good agreement between these two calculations and the difference is less than 0.01%.

3. Result and discussion

3.1. Fine-structure energy levels

The resulting M1 transition energies from the present RMBPT calculations for ions in Ag-like isoelectronic sequence with 62≤Z ≤94 are shown in Fig. 1. It is clear that the fine-structure energy separations increase rapidly and smoothly along the isoelectronic sequence. This confirms the argument by Grumeret al.in Ref.[18].

In Table 1, we present our RMBPT results of the finestructure energy separations for the isoelectronic sequence as well as other available theoretical and experimental data.The ExptDIRrepresents energy separations measured directly by the observation of the 4f2Fo7/2→2Fo5/2M1 transition lines.[10-12]These experiments were performed by using the EBIT facilities, including the CoBIT[13]in Tokyo-EBIT laboratory and SH-Perm EBIT[33]at the Shanghai EBIT laboratory. The ExptINDstands for the indirect measurements, that is, the transition energies are deduced from the other transitions involving the higher excited levels.[9]The values in the brackets are based on the interpolated values of 4f2Fo7/2.[9]The available theoretical works for Ag-like ions, that is, the MCDHF calculations (hereafter referred to as MCDHF1) by Grumerat al.,[18]the RMBPT calculations (RMBPT2) by Safronovaet al.,[14]the MCDHF calculations(MCDHF2)by Dinget al.,[17]and Ivanova’s results based on RPTMP,[15,16]are also displayed for comparison. In Fig.2,we illustratively show the differences of the fine-structure separation obtained by the present RMBPT calculations from other theoretical and experimental data. It is clear that our results are in excellent agreement with the direct measurements; the relative deviations between our results and the direct experiments are-0.16%,-0.13%,-0.11%,-0.06% and-0.03%, respectively, for the ions withZ=67, 68, 69, 70, and 74. The deviations decrease with increase ofZalong the isoelectronic sequence. It should be stressed that these direct measurements were performed only for the Ag-like ions with highZ.As point out in Ref. [11], for the ions with lowerZ, the M1 transition lines lie in the infrared range and the corresponding transition probabilities are very small, which may make the direct measurement of the M1 transitions more difficult.Compared with the indirect measurements[9]for the lower-ZAg-like ions, the deviations between our results and indirect experimental values become larger than those in high-Zions from the direct experiments. Moreover,we find that these indirect experimental data show an irregular trend along with the isoelectronic sequence. Therefore,we argue that the larger deviations may arise from the experimental errors,but it requires further measurements with higher precision.

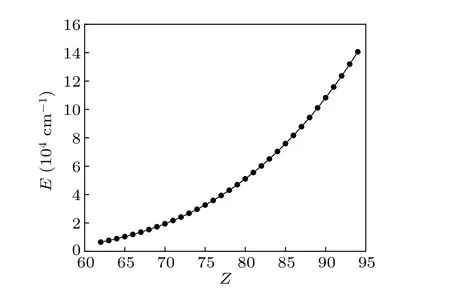
Fig. 1. Energies of the 4d104f 2Fo fine-structure separation along the Ag-like isoelectronic sequence as a function of nuclear charge Z.

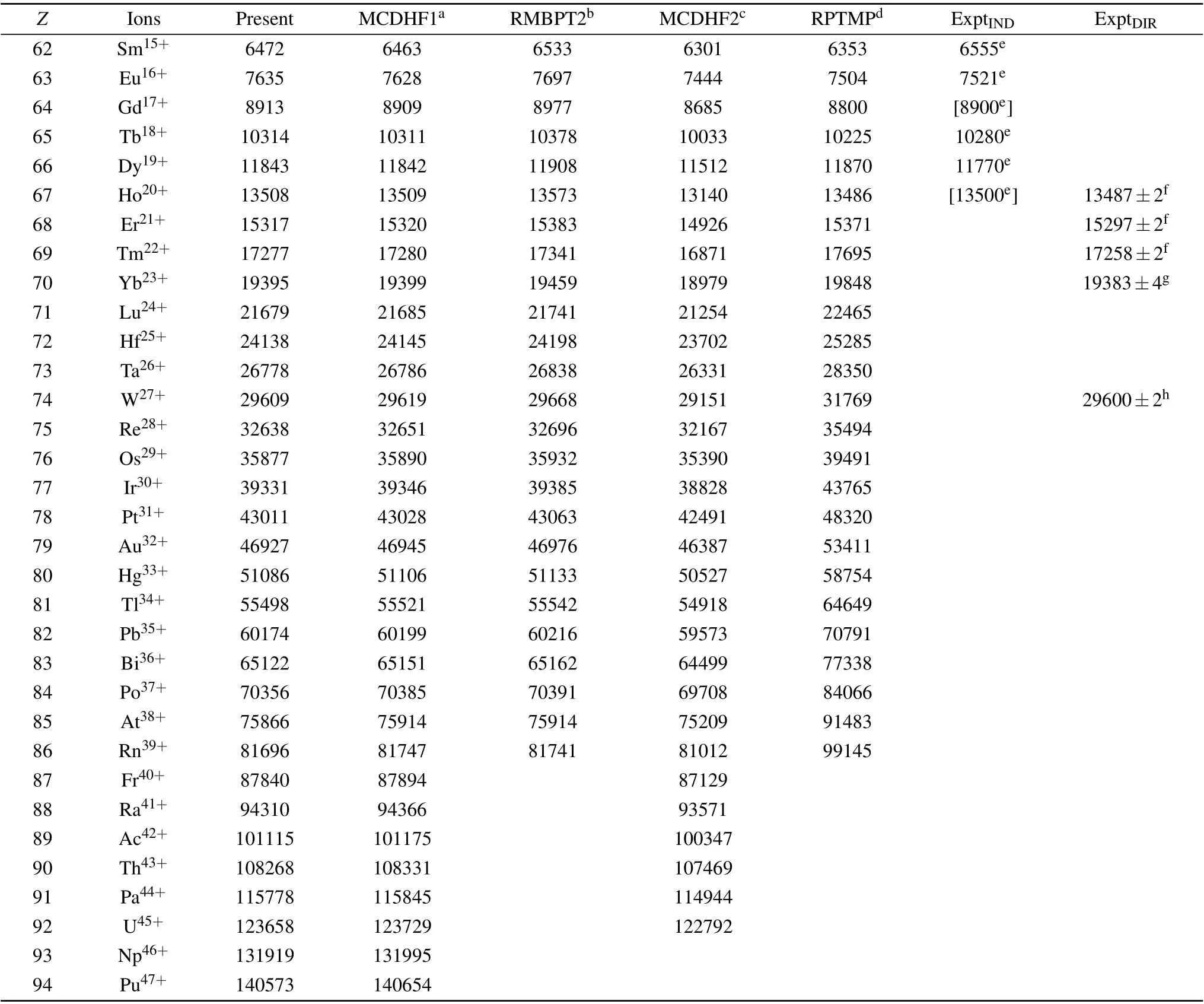
Table 1. Comparisons of the present 4f 2Fo5/2,7/2 fine-structure splitting with the experimental data and previous theoretical data from different methods MCDHF1,[18] RMBPT2,[14] MCDHF2,[17] RPTMP.[15,16] The ExptDIR and ExptIND are directly and indirectly measured fine-structure energies,respectively. In the column of ExptIND,the values in the brackets are based on the interpolated values of 4f 2Fo7/2. All energies are given in cm-1.

On the theoretical side, we compare our RMBPT calculations with the two existing MCDHF results[17,18]and the previous RMBPT2 calculations.[14]As shown in Fig. 2,our RMBPT calculations are in excellent agreement with MCDHF1 and RMBPT2 calculations for heavy Ag-like ions.For ions withZ ≥78, the relative deviations between these three results are less than 0.1%. As the nuclear chargeZdecreases, our RMBPT results and the MCDHF1 calculation still agree very well, and the largest difference is about 0.13% for Ag-like Sm (Z=62). However, the RMBPT2 results deviate from those by MCDHF1 and the present RMBPT results with decreasingZalong the isoelectronic sequence.Recently, Safronovaet al.[6,7]performed a new calculation for Ag-like Sm15+by employing the relativistic linearized coupled-cluster (CC) method and including all single, double, and partial triple excitations (SDpT). The relative difference between the present RMBPT calculations and their SDpT CC calculations for Ag-like Sm15+reduces to 0.43%,which is much smaller than that of the RMBPT2 results. From Fig. 2 we also observe that the discrepancies between the present and the MCDHF2 results are much larger than that from the MCDHF1 results and the latter has an irregular isoelectronic behavior. This may be due to the fact that only the CV correlation with 4dsubshell is included in the MCDHF2 calculations while the MCDHF1 and the present calculations consider the CV correlation withn=3, 4 shells. On the other hand,the deep-core-valence correlation contributes greatly to the final energy separations.[18]As discussed above, we believe that our RMBPT values and MCDHF1 values are more accurate compared with the MCDHF2 and RMBPT2 results,especially for the lower-ZAg-like ions. Finally, we compare our RMBPT calculations with the ones obtained with the RPTMP method.[15,16]calculations and other theoretical values.The inexplicable disagreement may arise from the inappropriate choice of the experimental reference values for the empirical model potentials used in the RPTMP calculations. Based on the above discussions,we suggest that the transition energies from the present calculations and MCDHF1 should be used as a reference.

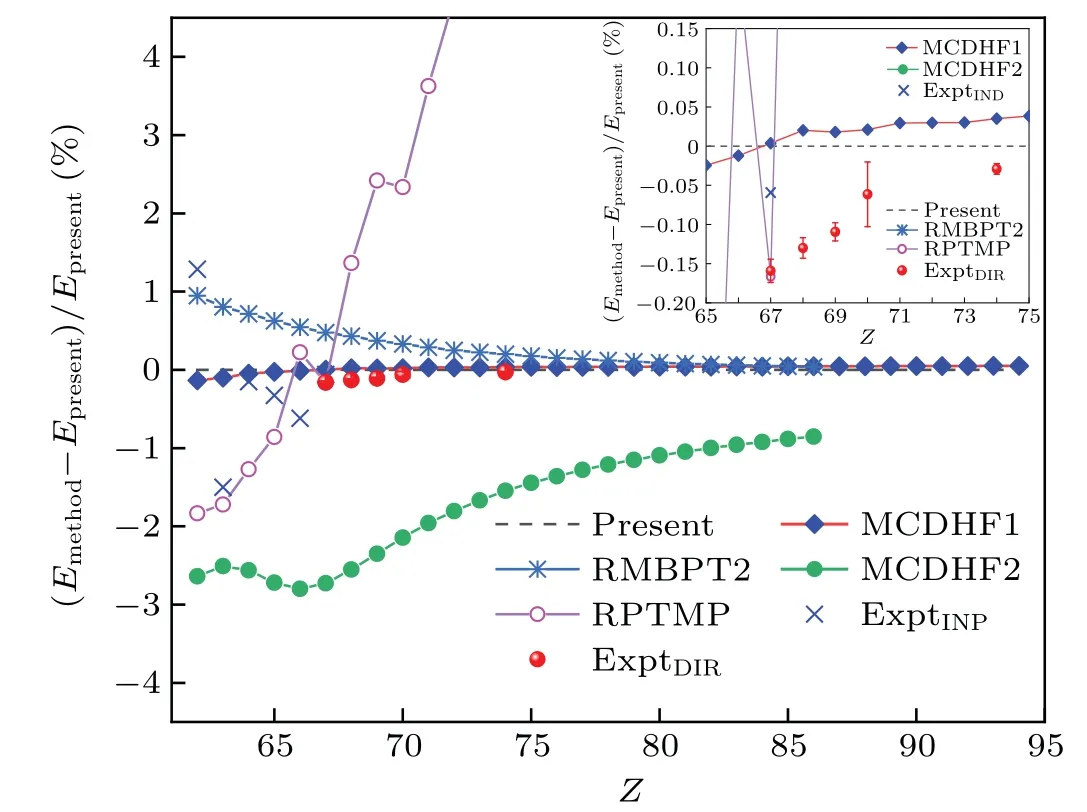
Fig.2. Percentage differences between the present and other theoretical and experimental fine-structure splittings of the Ag-like isoelectronic sequence as a function of atomic number Z. The ExptDIR and ExptIND represent directly and indirectly measured energy separations, respectively. Error bars of the direct experimental data points are available and included in the plot. The MCDHF1,[18] RMBPT2,[14] MCDHF2[17] and RPTMP[15,16] are earlier calculations.

3.2. Wavelengths and transition probabilities

In Table 2, we present the calculated (vacuum) wavelengths, transition rates and weighted oscillator strengths for M1 transitions between fine-structure energy levels in the 4d104f ground configurations of Ag-like ions along the isoelectronic sequence. The MCDHF1 calculations[18]are also given for comparation. In Fig.3,we compared theAvalues of the M1 transition obtained from the present RMBPT and those from the MCDHF1 method along the isoelectronic sequence.The differences of these two calculations decrease smoothly along the sequence,from 12.4%forZ=62 to 5.4%forZ=94.As shown in Table 2,the M1 transition rates are rather small,especially for the low-Zions. For such weak transitions, the agreement between the two independent calculations is satisfactory.

As shown in Fig. 2, the isoelectronic trend of RPTMP results[15,16]exhibits a significant deviation from our RMBPT

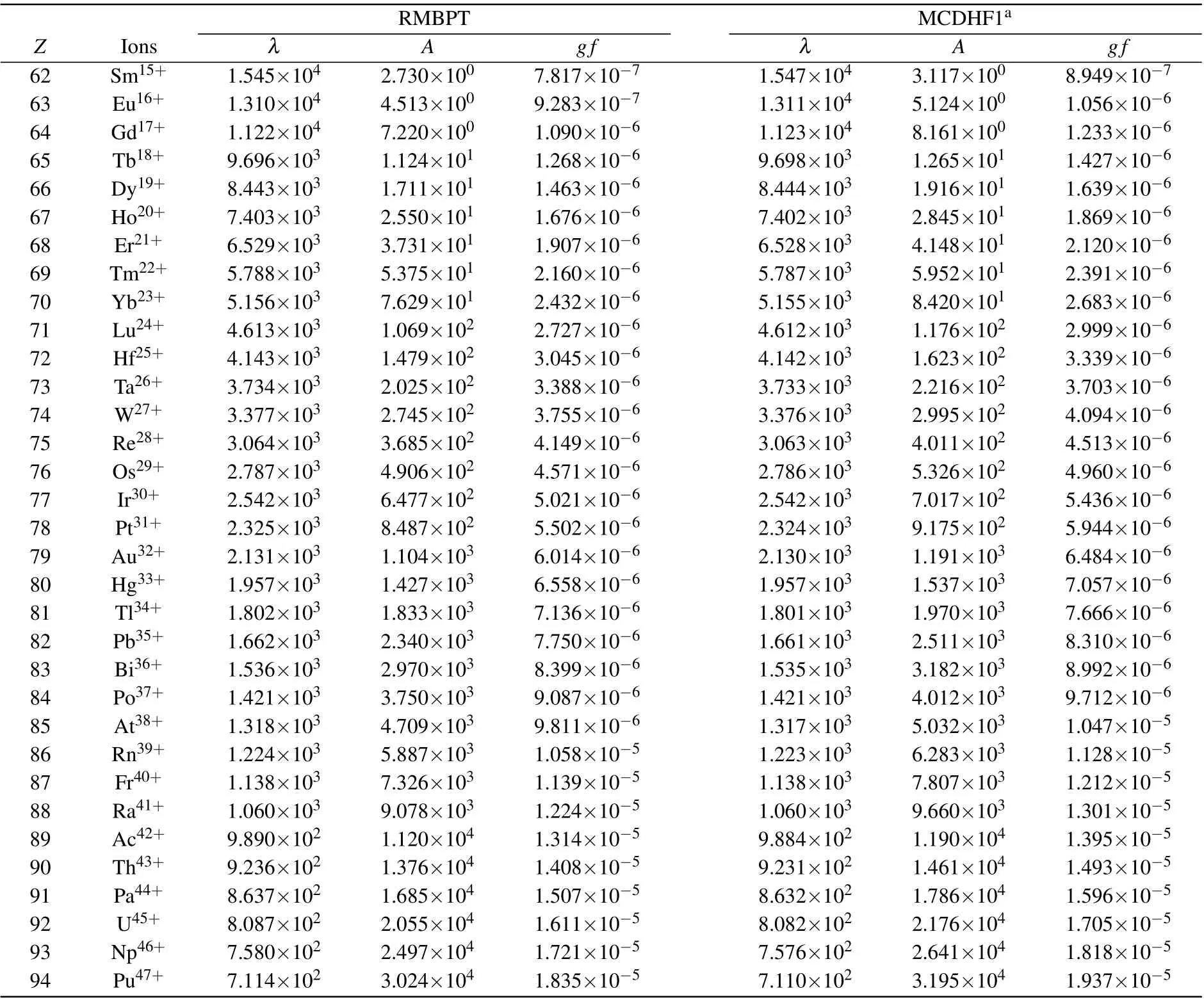
Table 2. Wavelength λ (˚A),transition rates A(s-1)and oscillator strength gf of the M1 transition between 4f 2Fo5/2 and 2Fo7/2 in Ag-like ions with 62 ≤Z ≤94,the MCDHF1 results[18] are also listed for comparison.

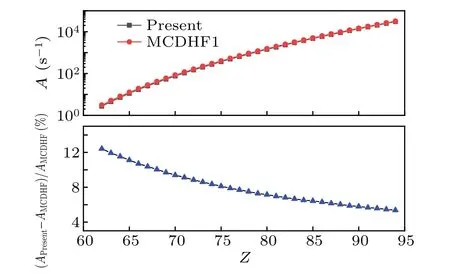
Fig. 3. Comparisons of the present calculated rates with those of the MCDHF1 calculations for the M1 4f 2F5o/ 2-2F7o/2 transition along the Ag-like isoelectronic sequence. The top panel shows the present Avalues and those from MCDHF1 and the bottom one is the differences between these two calculations.

4. Conclusions

In summary, we have calculated the M1 transition energies and rates in the ground configuration 4d104f of Aglike ions betweenZ=62 andZ=94 using the second-order RMBPT approach implemented in the FAC code. The present RMBPT energy separations show a smoothZ-dependence,and agree very well with the direct experimental data obtained from EBIT devices. The relative differences are less than 0.08%for Ag-like Yb23+and W27+,within 0.17%for Ag-like Ho20+,Er21+and Tm22+.Extensive comparisons of our wavelengths and rates for the M1 transition with the most recent large-scale MCDHF1 results[18]show that these two results are in good agreement with each other. For the fine-structure splittings, the maximum deviation between our RMBPT and the MCDHF1 results is less than 0.13%. For the transition rates, the relative discrepancies are less than～13% for all Ag-like ions concerned. We also demonstrate that for the ions at the beginning of the Ag-like isoelectronic sequence, our RMBPT and MCDHF1 results are more accurate than other theoretical values. Therefore,we believe that these two independent theoretical calculations can be used as the benchmark for the atomic data of Ag-like ions and will be useful for the line identifications of experimental spectra, as well as for the plasma spectra modeling and diagnostics in the fusion-plasma community.

Acknowledgements

This work is supported by the National Natural Science Foundation of China (Grant Nos. 11874090, 11934004,11404180, 11604052, and 11774037), and the National Key Research and Development Program of China (Grant No.2017YFA0402300).