Cross correlation mediated by distant Majorana zero modes with no overlap

Lupei Qin(秦陆培), Wei Feng(冯伟), and Xin-Qi Li(李新奇)

Center for Joint Quantum Studies and Department of Physics,School of Science,Tianjin University,Tianjin 300072,China

Keywords: Majorana zero modes,cross correlation,Andreev currents

1. Introduction

The nonlocal nature of the Majorana zero modes(MZMs) and the obeying non-Abelian braiding statistics promise a sound potential for topological quantum computation.[1-4]Throughout the past decade, the search for reliable MZMs has become a major theme in condensed matter physics.[5-11]In order to identify the Majorana zero modes (MZMs), rich transport phenomena have been proposed, such as the fractional Josephson effects,[12-15]peculiar noise behaviors,[16-25]and the famous Majorana quantized conductance 2e2/h.[20,22,26-28]Recent interests also include the nonlocal transport conductances[29-37]and the proposals to distinguish the nonlocal MZMs from the topologically trivial Andreev states.[38-43]

The most direct evidences of the genuinely nonlocal nature of the MZMs should be the Majorana teleportation[44-46]and/or the cross correlation of two remote Majoranas (γ1andγ2).[16-21]Both the phenomena of Majorana teleportation and nonlocal cross correlation are rather transparent by using the low energy effective Hamiltonian description, especially within the framework of“second quantization”in terms of the occupation-number-states|0〉and|1〉of the MZMs associated regular fermion (thefquasiparticle). Consider injecting an electron from outside into the superconductor through,for instance, the left MZMγ1. The occupation of the nonlocalfquasiparticle should allow for extracting a particle (either an electron or a hole) through the other distant right-side MZMγ2, thus expecting the so-called teleportation phenomenon.The same reason allows us to expect nonlocal cross correlation between the currents in the distant leads. More specifically, consider a two-lead (three-terminal) setup.[16-18,33-37]Can we find nonlocal cross correlation between the currents in different leads? A few studies showed that the cross correlation vanishes at the limit∊M→0.[16-18]

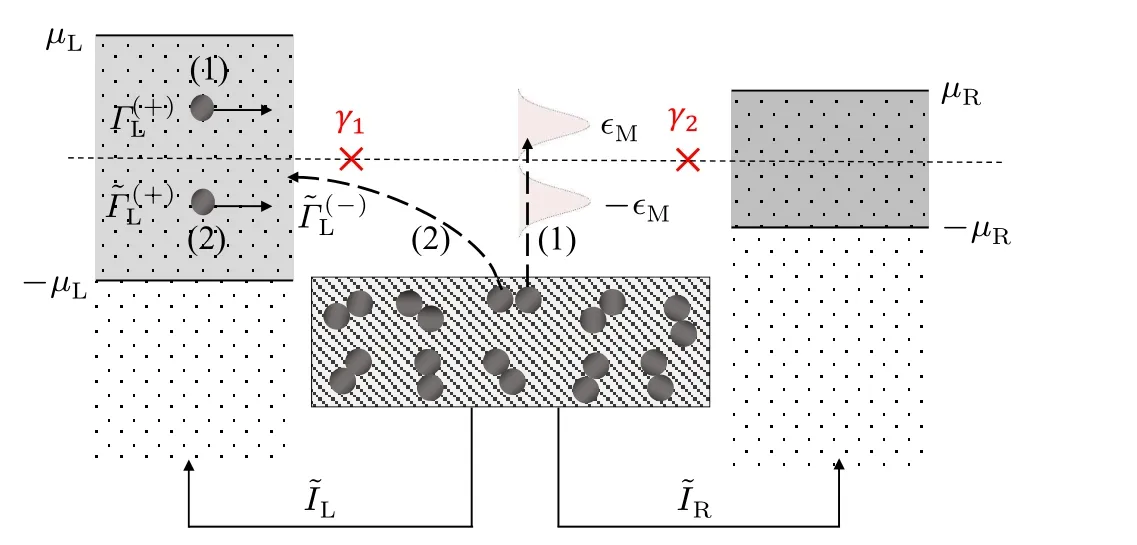
Fig. 1. Schematic circuit diagram for the Andreev reflection (AR) and inverse AR processes in the two-lead (three-terminal) device under consideration. In the AR process, taking the left lead as example, two electrons in the lead enter the superconductor,successively and coherently,and form a Cooper pair. The two electrons are of energy in resonance with (have Lorentzian centers at) ∊M and -∊M, respectively, as seen in Eqs. (3) and(4) in the text. The inverse AR process splits a Cooper pair and generates the excitation of an f quasiparticle in the superconductor, meanwhile,sends an electron back into the lead. In the plot,we only show the left-side current and the local Andreev process, while the right-side current and the crossed Andreev process can be similarly understood. In the diagram we also schematically show the net branch circuit currentsIL andIR, flowing back to the leads.

In this work,applying the master equation approach(and using the occupation-number-state representation), we show that it is possible by extracting component currents from the total lead-currents to expose the intrinsic nonlocal cross correlation between them, even at the limit∊M→0, owing to the nonlocal nature of the MZMs associatedfquasiparticle.Moreover, the component currents extracted from the total ones are nothing but the branch circuit currents flowing back to the individual leads from the superconductor,which are measurable in experiment, as schematically shown in Fig. 1. By combining together with the evidence of the zero-bias-peak of conductance(ZBPC),this nonlocal cross correlation should allow us to definitely confirm the existence of the nonlocal MZMs. This is the most important issue at present stage in the Majorana community.

2. Master equation approach

For completeness,we briefly outline the Majorana master equation(MME)approach based on Refs.[47,48],which deals with a pair of MZMs embedded in a two-lead(three-terminal)nonlocal transport setup. The low-energy effective description for a pair of MZMs can be commonly formulated by the HamiltonianHM= i∊Mγ1γ2,where∊Mis the coupling energy of the MZMsγ1andγ2. The Majorana operators are related to the regular complex fermion through the transformation ofγ1=f+f†andγ2=-i(f-f†). Through using the complex fermion representation, for a two-lead setup of transport, the tunnel-coupling of the MZMs to the leads is given by[19]

The master equation approach to quantum transport simply follows the theoretical treatment of quantum dissipation,where the system-of-interest is coupled to an environment usually via energy exchange, but not involving the particle exchange. For quantum transport, the system-of-interest is the central device, while the environment is the transport leads.In the transport problem,particle exchange/tunneling between the leads and the central device is seemingly causing certain difficulty to describe the central device by using the density matrix. However, after introducing the occupied and unoccupied probabilities of states,the fundamental requirement of Trρ=1 is guaranteed for the density matrix operatorρ. The transport master equation is thus well justified and has been applied broadly in practice.

where the broadening is given byΓ= ∑α(Γeα+Γhα)/2.This type of generalization in terms of the Lorentzian spectral function properly accounts for the level broadening effect, which directly follows the spirit of the self-consistent Born approximation[51]and works perfectly well for transport through single-level systems(such as the single-level quantum dot). This generalization makes the transport master equation applicable under small bias voltage,while it is well known that the usual Born-Markov-Lindblad master equation is applicable only under large bias limit(with voltage much larger than the level broadening widths). Here,in the Majorana case,the subgapfquasiparticle is simply a single-level system within the low-energy effective description. The only unique feature is the presence of the Andreev-process associated counterrotating-wave terms,which results in the two terms in the second round brackets in Eq.(2),while the two Lindblad terms in the first round brackets in Eq.(2)describe the normal tunneling process. We finally mention that,for the two types of process, the energy conservation is manifested differently in the rate expressions,i.e.,by the different centers of the Lorentzian spectral functionsδ(ω ∓∊M),see also illustration in Fig.1.

3. Transient current and its decomposition

The MME can be straightforwardly solved using the number-state basis{|0〉,|1〉}of the complex fermion (thefparticle). Let us denote the solution of the density matrix asρ=p0|0〉〈0|+p1|1〉〈1|. As an example,the left-lead current,

3.1. Unoccupied initial condition

Let us consider firstly the time-dependent solution under the initial condition of empty occupation of thefparticle state(nf=0),which reads

Here, the three transport coefficients (and the associated currents)correspond to,respectively,the local AR at the left lead,the crossed AR between the two leads,and the electron transmission from the left to the right lead. More explicitly,substituting Eqs. (3) and (4) into Eq. (9), we identify the transport coefficients as

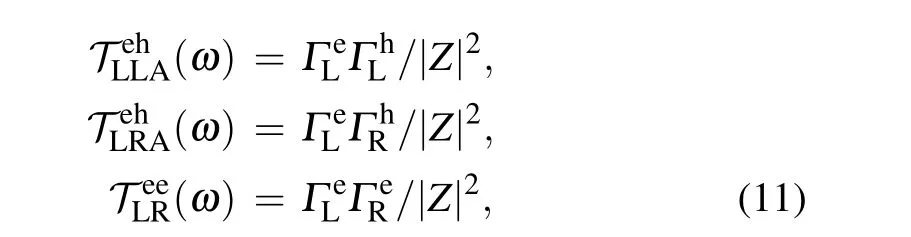
3.2. Occupied initial condition

In this subsection we briefly show the results for the initial condition of occupied state of thefparticle(nf=1). The time-dependent solution of the master equation reads

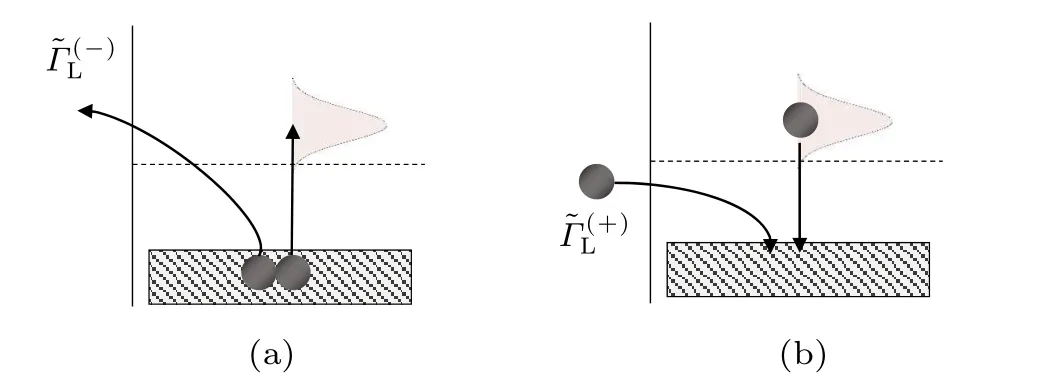
Fig. 2. Schematic diagram for transient contribution to the branch circuit currentIL, owing to the decay of the initial-occupation-channels. (a) The process contributing to I(2)L (B)given by Eq.(15)for the unoccupied initial condition,while I(1)L (B)given by Eq.(12)is not relevant to the branch circuit current. (b) The process contributing to I(2)L (B) given by Eq. (17) for the occupied initial condition, while I(1)L (B) is similarly not relevant to the branch circuit current.

4. Cross correlation of Andreev current fluctuations

As pointed out at the beginning of the previous section,within the formulation of rate equation(under the Markovian approximation),the total current,eitherILorIR,is not time dependent even in the transient process of the occupation probabilityp1(t).However,as analyzed later in detail,we know that the individual components of the current are time dependent and can show transient behaviors. Therefore, we may consider the cross correlation between the currentsILandIR, by deducting, from the total currentsILandIR, the components of the electron-electron and hole-hole transmission between

Finally,we obtain the current-fluctuation-correlator as

Here, we introduced the cross-correlation-factorCLR, which characterizes the essential correlation property,by noting that the time dependent behavior is relatively simple,and it simply leads to a Lorentzian lineshape～(ω2+4Γ2)-1in frequency domain.The most important point we would like to emphasize here is thatCLR/=0,even when the Majorana coupling energy∊M→0.

We notice that in Refs.[16-18]it was found that the cross correlation between the total currents in the different leads vanishes at the limit∊M→0. Here, despite using the totaloccupation-probability-description based master equation approach,we have successfully isolated the component currents(i.e., the branch circuit currents) from the total ones, and found nonzero cross correlation even at the limit∊M→0.In the occupation-number-state representation, the picture of nonzero cross correlation appears clear. Owing to the nonlocal nature of the MZMs associatedfquasiparticle,it is natural to expect that the disturbance at one side should influence the electron-hole excitation at the other side, leading thus to the nonlocal crossed AR process. In certain sense,the nonlocalfparticle is quite similar as the single-level electron in a quantum dot which,obviously,can correlate the currents in the two leads of transport. In the Majorana case, the left-side sum of the crossed AR and local AR currents, i.e., the branch circuit current considered in this work,is similarly correlated with the branch circuit current on the right side,through the nonlocalfparticle.

This current,generated by the inverse AR process,is negative.We then haveδIL<0 and arrive at the negative correlation as shown in Fig.3(a),by noting that the steady state current〈IL〉¯ρis positive.

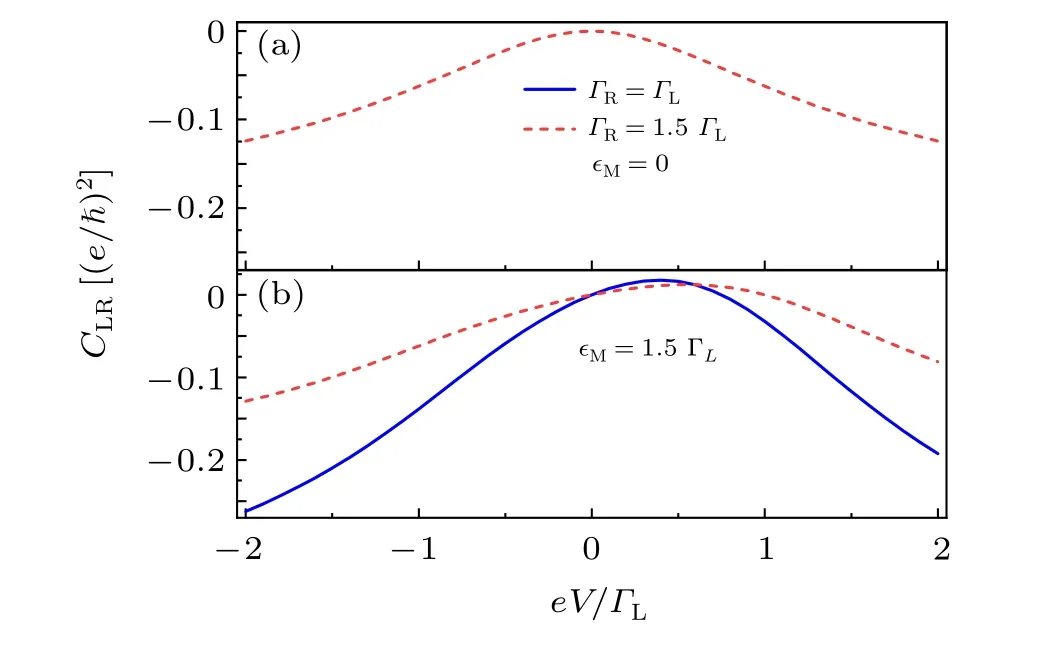
Fig.3. Cross correlation factor CLR as a function of the equally biased voltage considered in Ref.[17],i.e.,µL=µR=eV with respect to the chemical potential of the superconductor(∊F =0). In(a)and(b),results for the ideal(∊M =0) and nonideal (∊M /=0) Majorana cases are shown, together with the symmetric(ΓL=ΓR)and asymmetric(ΓL/=ΓR)coupling to the leads.

Fig.4. Cross correlation factor CLR as a function of the anti-symmetrically biased voltage,i.e., µL =-µR =eV with respect to the chemical potential of the superconductor.Other parametric explanation is the same as in Fig.3.

For the bias voltage dependence, the reason of the symmetric feature is relatively simple. That is, changing the bias voltage from positive to negative, the Andreev process is reversed. Then,the directions of both currents are reversed and the correlation of the current fluctuations keeps the sign unchanged. In Fig.3,the effect of asymmetry of coupling to the leads is also shown, for both the ideal (∊M=0) and nonideal(∊M/=0)cases.

5. Summary and discussion

Instead of the cross correlation between the total lead currents in a two-lead (three-terminal) Majorana device, we have analyzed the cross correlation of the Andreev-processassociated branch circuit currents. Despite applying a master equation approach,which deals with the total occupation probability of the MZMs associatedfquasiparticle,we have been able to successfully extract out the component currents from the total ones and computed the cross correlation by means of the quantum jump technique. Importantly, we found that the cross correlation does not vanish even when the Majorana coupling energy∊M→0,owing to the nonlocality nature of the MZMs. For different setup of bias voltage,we also found intriguing results of both negative and positive correlations and carried out simple physical understanding.

The proposed cross correlation can be measured as the usual power spectrum of current fluctuations, e.g., the noise spectrum calculated in Refs.[16-18],with the only difference by replacing the currents in the transport leads with the branch circuit currents flowing back from the superconductor to the individual leads,as schematically shown in Fig.1. The branch circuit currents are accessible,making thus the proposed cross correlation measurable in experiment. Combining with the evidence of the zero-bias-peak of conductance, the nonlocal cross correlation predicted in this work can help to confirm the nonlocal MZMs.

At present stage,the urgent challenge for Majorana confirmation is to distinguish the MZMs from the accidental nearzero-energy Andreev bound states.It seems that this challenge largely exists in the single-lead local conductance measurement,since both states would result in similar zero-bias-peak feature in the tunneling conductance. The difficulty seems improved in the two-lead cross correlation measurement. The key conclusion of this work is the nonvanishing cross correlation at the limit∊M→0,i.e.,with no spatial overlap between the two Majorana modes. We emphasize that the result will be drastically different for the case of Andreev bound states.This can be understood by applying the simplest model for the realization of a pair of Andreev bound states, following Ref.[43],where four MZMs are considered to form two regular fermions(f1andf2)at the two ends of a quantum wire.It is clear that the sub-gap state transport cannot support any cross correlation in the two-lead measurement,owing to the absence of any transmission channel between the left and right sides because of no coupling between thef1andf2quasiparticles(Andreev bound states). For the case of Andreev bound states,there exists only local Andreev process associated with, respectively,the localf1andf2quasiparticles,which makes the Andreev-bound-state difficult to be ruled out in the single-lead local measurement for Majoarana confirmation. However, in the two-lead transport measurement, both cases have qualitatively different results,say,zero or nonzero cross correlation.

Finally,from the result of Eq.(25),we see that the behavior of time dependence is relatively simple. The exponentially decaying function in time domain does not involve any quantum coherent oscillations. In practice, in order to be able to measure such type of quantum oscillations(e.g.,the Rabi oscillations of a qubit),the measurement speed should be faster than the quantum oscillations, which sets thus a requirement for the bandwidth of the measurement circuit.However,in our present case,the absence of quantum oscillations would relax the requirement for fast speed of measurement.Actually,from Eq.(25),we know that the transient process is slow,since the sub-gap state transport requires (Γ,eV)≪Δ, i.e., the tunnel coupling rate and bias voltage much smaller than the proximity effect induced superconducting gap. This slow transient process will make its measurement not more difficult than the measurements of current correlation functions in other contexts.

Acknowledgements

This work was supported by the National Key Research and Development Program of China (Grant No. 2017YFA0303304) and the National Natural Science Foundation of China (Grant Nos. 11675016, 11974011, and 61905174).