三江源典型地区1967—2019年降水时空演变特征
黎晓东,王永强,刘 万,许继军,瞿思敏
(1.河海大学 水文水资源学院,南京 210098; 2.长江科学院 水资源综合利用研究所(国际河流研究所),武汉 430010; 3.流域水资源与生态环境科学湖北省重点实验室, 武汉 430010)
1 研究背景
降水是水文循环的重要要素之一,受全球气候变暖影响,降水的时空特征发生了巨大的变化,这给降水时空演变带来极大不确定性[1]。青藏高原是全球气候敏感区之一,对全球气候变暖的反应十分灵敏,而三江源位于青藏高原腹地,生态环境极其脆弱,其降水时空特征受气候变暖影响更为明显[2-4]。果洛州位于三江源地区东部,境内黄河流长760 km,是三江源典型地区之一,在气候变暖影响下果洛州降水时空演变特征的变化将直接作用在黄河河源,对下游的水资源和水生态有着关键而直接的影响,因此,果洛州的降水演变特征在江源地区具备代表性和典型性。目前专家学者们已针对三江源降水趋势开展了相关研究,利用1960—2015年三江源多个观测站实测资料分析了该地区降水变化趋势,发现三江源地区降水呈不显著增加趋势,且三江源降水季节和区域差异明显,其中典型区域如达日、班玛等地秋季降水减少明显[5-6]。为更好描述三江源典型区域降水时空演变特征,本文在上述研究的基础上针对三江源典型区域进行长时间序列的降水时空演变特征分析,完善前述研究未涉及的黄河河源地区长时间序列降水时空演变特征,为准确分析三江源地区气候变化原因、水文循环过程提供重要的科学依据。
2 研究资料与方法
2.1 研究区域概况
果洛州面积约76 442 km2,位于三江源地区东部(图1),占黄河源地区总面积的60%,经纬度范围为96°54′E—101°51′E,32°31′N—35°37′N,果洛州下辖玛沁、甘德、达日、久治、斑马和玛多6个县,总人口约21.15万人,以牧业为主。果洛州平均海拔约4 500 m,且海拔为4 000~6 000 m的地区面积占总面积约80%,地形起伏不大,高差多在500~1 000 m之间,坡度较缓;气候类型属于典型高原大陆性气候,气温低、干燥寒冷,年均降水量约440 mm,年均气温约-4 ℃,最冷月平均气温为-12.1 ℃,全年无绝对无霜期。境内主要河流为黄河和大渡河,其中黄河境内流程约760 km,西北部包含扎陵湖和鄂凌湖2个淡水湖。土地类型以草地为主,草地面积占总面积的75%,多为山地草场和草甸植被,另还有林业用地面积5 324.6 km2,包括原始森林面积208.5 km2,疏林地90.7 km2,灌木林地5 004 km2,无林地21 km2。果洛州境内河流纵横,湖泊遍布,有大小河流36条,水域面积1 600 km2,淡水储量177.7亿m3,其中地下水储量44.6亿m3,地表水储量133.1亿m3。

图1 果洛州地形、境内站点及相对三江源的地理位置Fig.1 Topography and meteorological stations ofGuoluo in the headwaters of the Three Rivers
2.2 研究资料
考虑资料数据长度及代表性,本文选取了果洛州境内玛多、达日、班玛3个气象站1967—2019年共53 a的降水观测数据进行分析,数据来源于中国气象数据共享服务网。
2.3 研究方法
选取果洛州3个代表观测站,对果洛州降水的时空演变特征进行具体分析。通常,采用趋势分析、突变分析和周期分析等方法进行降水的时间变化特征分析,采用降水空间分布叠加在高程上进行空间变化分析[7]。趋势分析中,首先进行基本统计参数的计算,绘制年际变化曲线及5 a滑动平均曲线来反映年际变化,随后采用Mann-Kendall趋势检验法分析趋势演变显著性,并基于R/S分析法[8]判断趋势演变持续性。突变分析中,采用Mann-Kendall突变检验法和滑动平均差检测法[9]检验降水时间序列的突变点。周期分析中,采用Morlet小波分析法分析降水时间序列的周期性。
2.3.1 Mann-Kendall趋势检验法
Mann-Kendall趋势检验法中,设时间序列数据(x1,x2, ... ,xn)是n个独立同分布的随机变量样本,且没有显著趋势。定义统计量S为
(1)
式中:n代表时间序列样本个数;xi和xj分别代表时间序列中相应年份的数据。其中
(2)
构造M-K统计量Z为
(3)
Z为正时表示上升趋势,Z为负时表示下降趋势。若Z的绝对值大于给定显著性水平下的临界值,则说明趋势显著,否则不显著。
使用Mann-Kendall倾斜度β来量化单调趋势[10],则

(4)
当β>0时,反映上升趋势;当β<0时,反映下降趋势;β数值越大,趋势越显著。
2.3.2 R/S分析法
时间序列趋势统计检验法R/S分析法计算得到的Hurst指数能够定量描述时间序列演变趋势的持续性,可判断未来趋势相对于过去趋势的变异程度,基本原理如下所述。
考虑一个时间序列ξ(t),t=1, 2,…,n,对于任意正整数τ≥1,定义均值序列为
(5)
累积离差X(t)表示为
定义极差R为

τ=1,2,…,n。
(7)
定义标准差S为
当ξ(t),t=1, 2,…,n,不是相互独立、方差有限的随机序列时,必有
(9)
也即
(10)
式中:c为某常数;H为Hurst指数。
显然时间序列分段数τ为变量,lg(R/S)τ为关于τ的一次函数,那么Hurst指数H表现为该一次函数的斜率。
Hurst指数可以判断时间序列的持续性,表征未来趋势相对于过去趋势的变化情况,持续性越强,未来变化趋势与过去变化趋势越相似。Hurst指数的分类见表1。

表1 Hurst指数分类Table 1 Classification of Hurst index
2.3.3 滑动平均差检测法
基于滑动平均差检测法对时间序列xi(i=1, 2,…,n)的突变性检验步骤如下所述。
分别构造正向和逆向滑动平均序列,即:
i=2,3,…,n,k=min(p,i-1);
(11)
i=2,3,…,n,k=min(p,n-i+1) 。
(12)
计算正逆向滑动平均序列差即
ΔMi=|MUi-MDi| 。
(13)
式中p为变量的常规物理周期。将这些序列差进行排序,统计量ΔMi的极大值表示该样本点前后子序列均值发生了急剧变化,即极大值点为该时间序列突变点。
2.3.4 Mann-Kendall突变检验法
对时间序列xi(i=1, 2,…,n)构造一秩序列,即
(14)

定义顺序统计量为
(15)
式中:UF1=0;E(Sk)是Sk的期望;Var(Sk)是Sk的方差;且UFk~N(0, 1)。
此时将序列xi(i=1, 2,…,n)逆序,用同样的方法计算逆序统计量UBk,同时使UBk=-UFk(k=n,n-1,…, 1),UB1=0。将UFk和UBk绘制到同一幅图上,若UFk和UBk两条曲线超过临界线,表明上升或下降趋势显著;若UFk和UBk出现交点且交点在临界线之间,则该交点对应的时间点为发生突变的时间点,且突变显著[11]。
2.3.5 Morlet小波分析法
给定小波函数Ψ(t)为
(16)
式中:t为时间;c为无量纲频率,常数,且当c≥5时Morlet小波就能近似满足允许性条件,这里取c=6.2;i为虚数单位。
水文时间序列x(t)的连续小波变换系数为
式中:a为尺度因子;b为平移因子;t为时间序列下标。
将时间域上关于a的所有小波变换系数的平方进行积分,即小波方差为

(18)
将式(18)具象后得到的小波方差图能够反映信号波动的能量随尺度a的分布,对应峰值处的尺度为该序列的主要周期[12]。
3 研究结果分析
3.1 降水年际变化趋势分析
1967—2019年果洛州的降水量基本统计参数见表2。从表2可知:果洛州的降水年际变化波动不大,果洛州面平均降水53 a内的变差系数Cv值为0.20,整体变化较平稳,除玛多站波动较为明显外,其他站点的Cv值较小;面平均降水和各站的线性趋势倾向率均为正,果洛州面平均降水线性倾向率为4.01 mm/a,增率较大,其中达日站线性倾向率高达5.58 mm/a,整体呈现出较为显著的递增趋势。倾斜度β均>0且数值较大,表明降水年际变化递增趋势较为显著。M-K趋势检验统计量Z结果显示,果洛州面平均及各站点的Z值均为正且通过了0.05显著性水平检验,表明果洛州降水年际变化呈现显著的递增趋势。

表2 1967—2019年果洛州降水量基本统计参数Table 2 Characteristic parameters of precipitationin Guoluo from 1967 to 2019
1967—2019年果洛州的降水年际变化曲线、线性趋势及5 a滑动平均见图2。从图2(a)可知,果洛州面平均及各站点降水年际变化呈现为明显的逐渐增加趋势,且在1981年之前降水量明显偏少,而1980年之后降水量明显偏多,1980年左右存在明显的降水量跳跃突变;5 a滑动平均结果也显示,1980年左右果洛州的降水变化趋势存在明显跳跃突变。除跳跃突变外,年际变化和5 a滑动平均结果均显示,1980—1990年间果洛州面平均降水量存在微小的波动,而1990年之后波动趋于平稳,玛多站波动相对较大,在1980—1990年、2005—2015年间存在小幅度波动,达日站、1981年后班玛站则在一直处于一个相对小幅波动状态。

图2 果洛州1967—2019年降水量年际变化曲线Fig.2 Inter-annual variation of precipitation in Guoluo from 1967 to 2019
对果洛州1967—2019年面平均降水序列进行R/S分析,得到Hurst指数为0.90,表明趋势演变呈现强持续性,即未来降水演变趋势与当前降水演变趋势基本一致,继续保持递增。
综上所述,1967—2019年果洛州降水年际变化呈现为显著的递增趋势,且年际变化曲线显示果洛州年际降水在1980年左右存在较为明显的跳跃突变,果洛州年际降水未来的演变趋势将与目前的演变趋势保持一致。
3.2 降水年际突变分析
1967—2019年果洛州面平均降水年际的突变情况见图3和图4。从图3可以看出,M-K突变检验法分别检测到1967—2019年果洛州面平均降水,以及玛多站、达日站和班玛站降水序列在1982年、1985年、1988—1989年间和1978—1979年间发生突变,其中仅班玛站UFk和UBk交点落在临界线内,即除班玛站之外其他突变点不显著。另外,果洛州面平均降水、玛多站、达日站和班玛站的UFk曲线在交点之后均在临界线之外,表明降水年际变化自突变点之后保持显著的上升趋势。

图3 M-K突变检验法检测突变点Fig.3 Result of abrupt change detected byMann-Kendall test
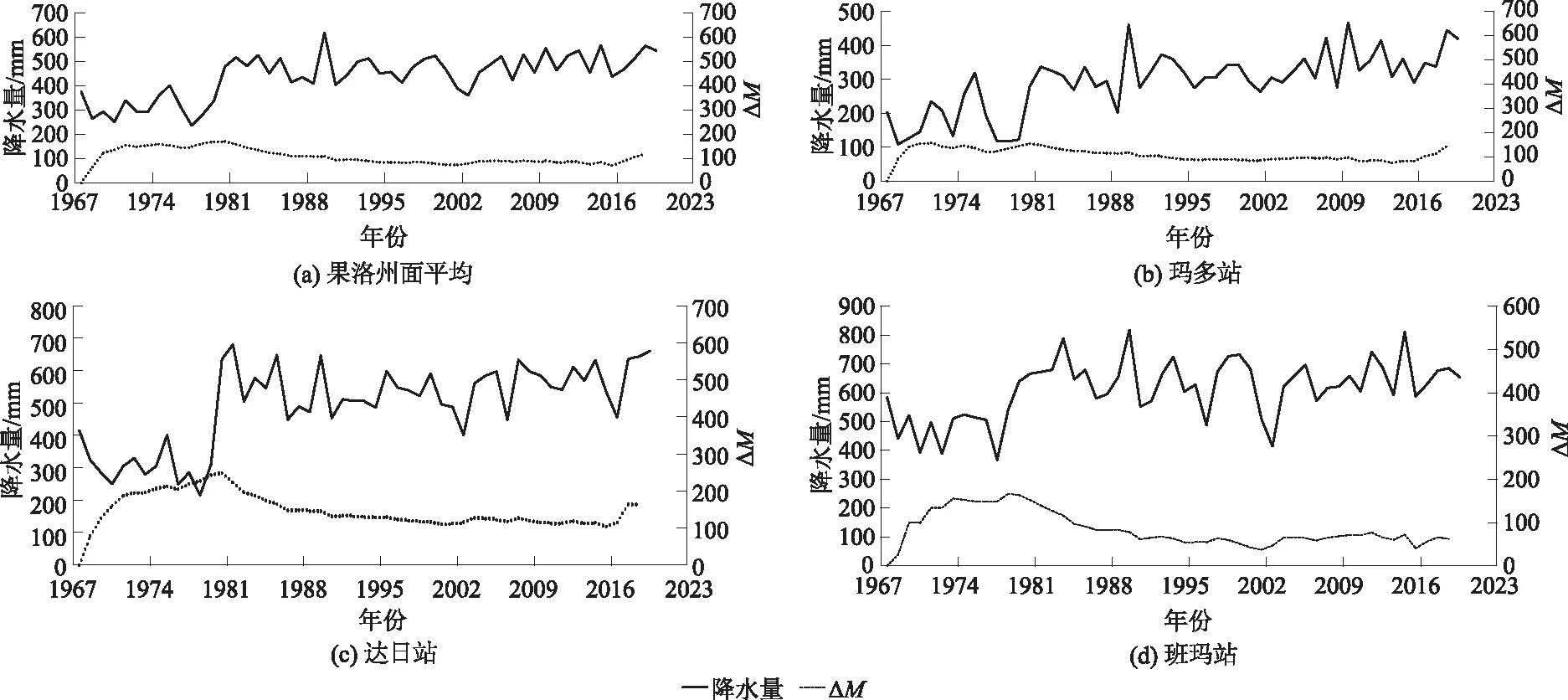
图4 滑动平均差检测法检测突变点Fig.4 Result of abrupt change detected by moving average method
从图4可知,滑动平均差检测法检测到1967—2019年果洛州面平均降水、玛多站、达日站降水序列在1980—1981年间发生突变,与M-K突变检验检测到的结果相比更靠近图2(a)—图2(c)显示的突变时间点;检测到班玛站在1978—1979年间发生突变,这与M-K检验结果一致,且都符合图2(d)发生突变的时间点。相比之下,滑动平均差检测法的检测结果比起M-K突变检验更符合3.1节的分析。
综合3.1节的分析和本节的分析可知,进行趋势性检验之所以如此显著,是因为在突变点前后降水序列的均值差异非常大,在进行全时段拟合和分析时容易得到显著的递增趋势的结论。表3对突变前后的降水年际序列基本统计量进行了对比,可以看到,突变点之后的均值增幅非常明显,果洛面平均降水增幅为55%,玛多站的增幅几乎翻倍。突变点之后的降水年际变化波动较小,Cv值分布在0.11~0.17之间,与3.1节的分析一致。突变后的线性倾向率均不如表2所示的大,但果洛面平均、玛多站、达日站的M-K趋势检验均通过了0.05显著性水平检验,即降水年际变化趋势是显著增加,与3.1节分析一致,而班玛站则呈现为不显著的减少趋势,不同于果洛州主要的降水变化趋势。

表3 突变点前后降水基本统计参数对比Table 3 Comparison of precipitation characteristicparameters before and after abrupt change
3.3 降水年际周期分析
果洛州1967—2019年面平均降水小波系数实部等值线见图5。根据图5可知,时间尺度26~29、20~22、12~15、5~ 8 a表现非常明显,遍布了整个时域;中心尺度大约分别为28、21、13、7 a。但是28 a尺度等值线变化频繁,表明这一时间尺度的面平均降水存在较明显的波动。

图5 1967—2019年果洛州面平均降水小波实部等值线Fig.5 Wavelet coefficient real part of areal averageprecipitation of Guoluo from 1967 to 2019
基于Morlet小波分析法分析1967—2019年果洛州面平均降水小波方差见图6。根据图6可知,果洛州面平均降水存在不同尺度的周期变化,小波方差图存在4个明显的极值,分别为28、21、13、7 a。其中28 a时间尺度对应的极值最大,表明28 a左右的周期震荡最强,是面平均降水量变化的第一主周期,即1967—2019年果洛州面平均降水量存在以28 a变化的主要周期,这一周期的波动,决定着该地区年降雨量的变化特性;21、13 a分别为第二主周期、第三主周期;周期7 a尽管实部等值线分布均匀,无明显交替,但因小波方差极值远不如前述3个周期来得大,以7 a为1967—2019年果洛州面平均降水周期不具备足够的代表性。

图6 1967—2019年果洛州面平均降水小波方差Fig.6 Wavelet variance of areal average precipitationof Guoluo from 1967 to 2019
3.4 降水年际空间特征分析
1967—2019年果洛州面平均降水空间分布特征见图7。根据图7(a)可以看出,区域降水量在空间分布上整体呈现由西北向东南方向递增的规律,形成自西北降水量293 mm极小值递增逐渐汇合至东南角693 mm极大值的闭合曲线的分布格局。根据图7(b)可以看出,降水空间分布与地形高程有关,4 200 m以上海拔地区平均降水量约370 mm,3 500 m及以下海拔、河谷地区平均降水量约560 mm,降水随高程变化差异明显。
4 结 论
(1) 1967—2019年果洛州面平均降水时间序列M-K趋势检验统计值Z为4.96,线性倾向率为4.01 mm/a,呈显著增加趋势。果洛州1967—2019年降水整体波动Cv值为0.20,发生突变之后,降水年际Cv值为0.11,变化过程相对稳定。果洛州1967—2019年降水年际变化Hurst指数为0.90,当前演变趋势具有强持续性。
(2) 1967—2019年果洛州降水时间序列在1980—1981年发生显著突变,班玛站相对提前。突变前后降水量发生明显变化,面平均增加55%,达日站增幅近2倍。滑动平均差检测法检测到的突变点与年际变化曲线显示的突变点更接近,Mann-Kendall突变检验法检测到的突变点大多滞后且不显著。
(3) 1967—2019年果洛州面平均降水存在以28 a为第一主周期、21 a和13 a分别为第二、第三主周期的周期变化特征。
(4) 区域降水量在空间分布上整体呈现由西北向东南方向递增的规律,形成自西北极小值293 mm逐渐递增汇合至东南角极大值693 mm的闭合曲线的分布格局。降水空间分布与地形高程有关,4 200 m以上海拔地区平均降水量约370 mm;3 500 m及以下海拔、河谷地区平均降水量约560 mm;降水随高程变化差异明显。

