基于多元线性回归模型的水质优化研究
黄克勤,吴海洋,贾德庚
(广元中孚高精铝材有限公司, 四川 广元 628000)
1 建模与参数估计
根据过去的一年中每月补水情况(采用纯水与工业水的添加比值)、排污量、月平均气温(来源为气象局网站)统计了一组影响因子的数值,收集每月对应的氯根化验结果,在模型中使用纯水和工业水添加比例的因子,实验数据如表1所示。

表1 实验数据统计表
假设因变量氯根Y与自变量纯水/工业水比例x1、月平均温度x2、排污量x3之间满足公式(1):
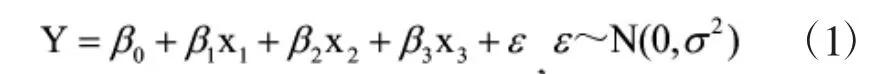
式中:β0、β1、β2、β3为回归系数[2],为了计算四个回归系数的值,需要对(x1,x2,x3,Y)进行12次观察实验,设线性方程式:(xi1,xi1,xi1,Yi),i是一个容量为12的样本,即i=1,2…11,12,可以得到如公式(2)的样本模型:
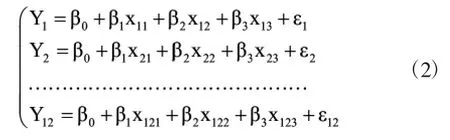
结合本设计中的实验数据,将公式(2)用矩阵表示为:
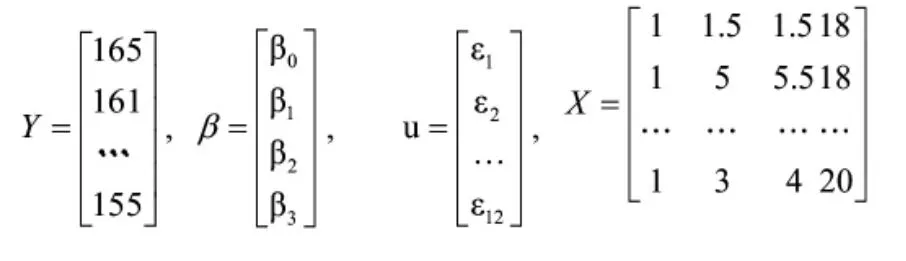
则
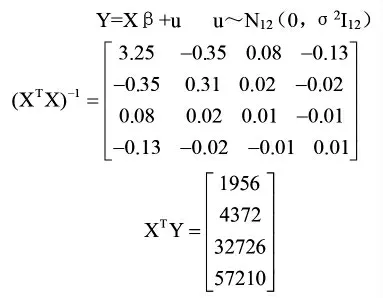
所以
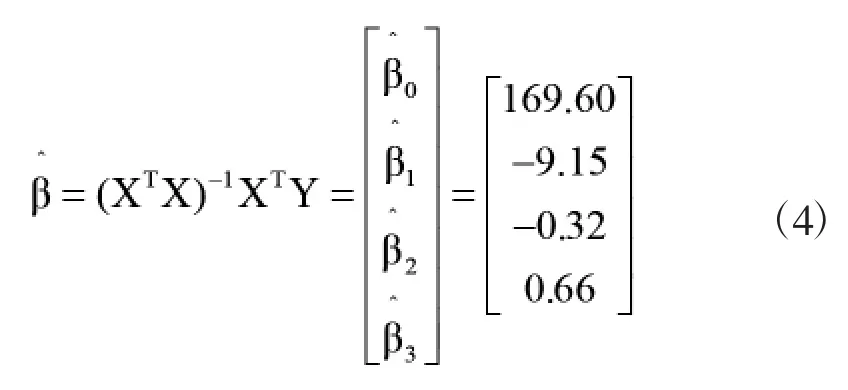
故氯根浓度与纯水/工业水比例x1、月平均温度x2、排污量x3之间的线性回归模型为:
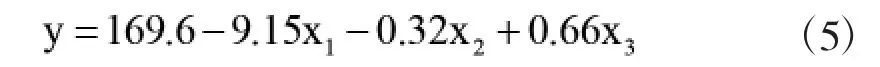
2 模型检验
2.1 线形模型有效性检验
如果要检验氯根浓度与纯水/工业水比例x1、月平均温度x2、排污量x3三个变量之间是否存在线性关系,只需验证β1,β2,β33个回归系数是否同时为0。如果回归系数均为0,即不存在明显线性关系,检验结果为线性回归不显著;反之则认为线性回归显著,因此,假设:

将12组观察值代入公式(6)中,检测是否成立。若12组观察值均满足公式(6)所呈现的关系式,检验结果为线性回归不显著;反之,若12组观察值不全满足公式(6),检验结果为线形回归显著。当H0成立时,有:
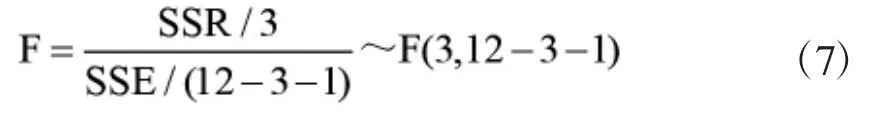
如果F值较大,更精确的说,即当SSR/SSE比值较大时,则说明自变量x对Y的线性作用大于回归系数对Y的线性作用,此时可以认为H0不成立;如果F值较小,则说明回归系数对Y起主要作用,因此H0成立。现给定显著性水平α为0.05,对模型进行检验:
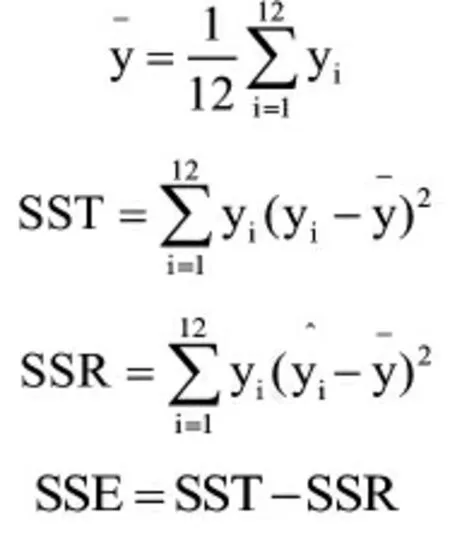
代入计算后得F=16.19。
又因为α=0.05,所以:
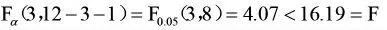
因此线性模型显著。
2.2 回归系数的显著性检验
在此三元线性模型中,在经由线性模型有效性检验之后,可以得知:因变量氯根浓度Y和自变量x之间存在显著线性关系,但由于自变量的不同,每个自变量xi对氯根浓度Y的影响不尽相同。因此在线性模型进行有效性检验之后,可以忽略对氯根浓度Y产生影响微乎其微的自变量xi,只保留有效的重要因素,优化为简洁的线性模型,以便有利于实际应用。故,xi对Y的检验假设:
H0:β1=0,β2=0,β3=0
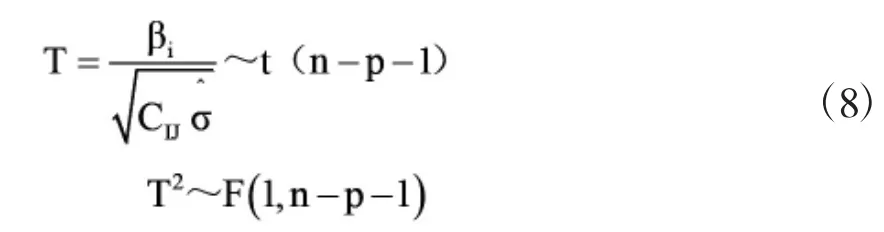
得到拒绝域:
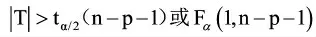
如果检验结果接受H0,即βi=0,应将xi从回归方程中删除,如果有多个变量对Y的影响不显著时,则每次只能删除一个变量,重新建立回归方程后,再进行重复检验。

所以对β1,β3的检验结果拒绝H0,β2的检验结果接受H0,即纯水/工业水比例、排污量对氯根浓度的影响显著,环境温度对氯根浓度的影响不显著,应将其从回归方程中删除。
3 回归方程的改进
根据上一节对回归系数显著性检验的结果,删除回归方程中的环境温度影响因子,将剩下的两个影响因子重新进行建模和模型检验,得到如下结果:
回归方程为:
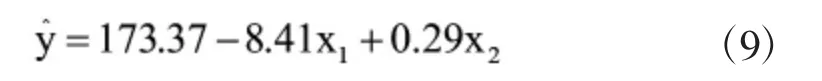
线性模型有效性检验:F0.05(2,9)=4.26<20.28=F,模型显著;
回归系数显著性检验:
T12=31.24>F0.05(1,9)=5.12;
T22=7.56>F0.05(1,9)=5.12;
因此β1,β2都显著不为0,剩余的两个因子纯水/工业水比例、排污量都能够显著影响氯根浓度。
4 预测
假设获得了x1,x2这样一组新的观察值,记为(x01,x02),则可以根据公式1-1获得点预测[3]。
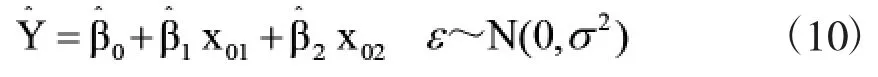
区间预测:

其中:
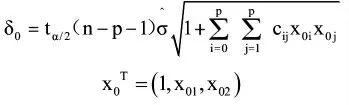
现对x01=2.2,x02=26,相应y0的置信度为0.95的区间进行预测。
根据公式2 得到y0=162.41;t0.025(9)=2.2622;σ=
即氯根离子的浓度置信度为0.99的预测区间为(155.94,168.88)。
5 验证
依据改进后的回归模型,在9月和10月份对对实际效果进行验证,如表2所示:

表2 氯根浓度的预测和验证结果对比
最近两个月的验证结果在预测区间(155.94,168.88)内,达到预期效果。
6 结论
本文主要是针对铝业公司散热器在运行中遇到的问题进行分析,针对影响散热器寿命的氯根腐蚀问题进行建模、改进,为后续维护管理提供决策依据,总结如下。
(1)结合实际,确定了温度、排污量、纯水添加比例三个对氯根浓度影响较大的因子,每月采集实验数据。
(2)根据实验数据,利用高等工程数学知识,建立了氯根浓度与影响因子之间的多元线性关系。
(3)利用改进设计后的方程进行数据预测,为详细掌握氯根浓度提供科学依据。

