考虑从众阈值和主体特征的人群疏散元胞自动机模型*

刘以雪，毛占利，廖明煜，3

(1.中国人民警察大学，河北 廊坊 065000；2.北京市海淀区消防救援支队，北京 100091；3.广东省建筑科学研究院集团股份有限公司，广东 广州 510500)

0 引言

当大型公众聚集场所发生紧急情况时，人员会表现出特殊的疏散行为，不同人群行为会催生出不同人群现象。部分学者采用数值模拟对人员疏散进行研究，常用模型包括元胞自动机(Cellular Automata，CA)[1-3]模型、社会力[4]模型及Agent-Based Model (ABM)模型[5]。Helbing等[6]认为从众行为是人员在群体中表现出的一种趋势，即与他人行为保持一致；Malid等[7]通过对比实验与模拟结果，重点关注人员疏散决策阶段的从众影响；Lovreglio等[8]提出人员在疏散决策时主观认知能力起决定性作用，社会性影响是人员表现出从众行为的原因之一；曹爱春等[9]建立了1种基于多主体与元胞自动机模型相结合的大型体育场馆人群疏散模型；Saloma等[10]对人群的从众程度进行量化，研究从众行为影响疏散时间的临界状态。

本文将元胞自动机与基于主体的疏散模型相结合，通过引入从众阈值概念，讨论从众行为对疏散效率的影响及临界状态。元胞自动机与基于主体的模型相结合，可以强调个体的认知判断能力差异，同时确保系统具备时序逻辑，实行动态演化。通过对从众行为的程度进行量化，可计算最有利疏散的临界值，对人群疏散研究具有现实指导意义。

1 理论描述

1)人群疏散的从众行为

大规模人群在紧急情况下会表现出不同的人群行为和人群现象，此时人员的行为受其身边人的影响较大，在实际事故中存在疏散者选择跟随他人行动路线的趋势，在视野受阻或信息不足时尤为明显。当人群试图逃离充满烟气的双出口房间时发生从众行为，导致一侧出口发生堵塞[11]。人群疏散的从众行为与其他疏散行为现象具有一定关联，研究时会将其与小群体行为、信息传递行为、成拱现象等共同讨论[12-13]。

2)基于主体与元胞自动机的模型

元胞自动机模型具有强大的计算能力，能够充分考虑系统中的环境因素影响，但该模型忽略了个体差异性、空间离散化对人群疏散行为的影响。基于主体的模型(ABM)通过将系统中个体定义为主体，关注个体的特征属性设定，可充分考虑人员运动能力、心理承受、认知能力等方面的差异，但在人员运动及整体动态变化方面有所欠缺，且计算量较大，不适用于大规模人群的模拟。结合2个模型优点，聚焦人群的从众行为，力求更加真实、全面地模拟人群疏散行为与现象，提出基于主体的元胞自动机疏散模型(CA-Agent)。

2 模型建立

2.1 空间与运动状态设定

基于主体(Agent)与元胞自动机的人群疏散模型建立在二维的元胞网格内，元胞大小设置为0.4 m×0.4 m，任意单元格在任意时刻只能由1个主体占据，根据网格位置可确定每个主体位置，采用Moore型[14]邻域表示人员可能的运动方向。边界为疏散空间围墙和安全出口，人员一旦离开出口表明疏散成功。

1)运动角度

人员在划定区域内的疏散运动由运动角度和运动速度确定。主体在元胞中每次位置的更新均伴随运动速度与运动角度的变化，用以模拟真实情况下人群疏散运动过程。由于主体间相互影响，主体运动角度和运动速度均发生变化，故对主体运动角度与运动速度进行规则设定，其中运动角度的变化由主体与安全出口的相对位置及主体前一时刻运动角度决定，主体运动角度由其在t时刻的坐标位置与安全出口位置组成的角度和邻域内其他主体在t-1时刻运动角度的均值决定。

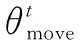
(1)

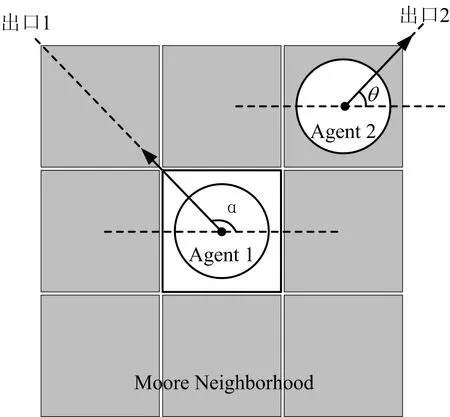
图1 主体1受邻域内主体2影响的运动方向示意Fig.1 Schematic diagram for movement direction of agent 1 influenced by agent 2 in neighborhood

2)运动速度

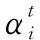
(2)

(3)

人员在疏散过程中的运动速度主要受人员自身运动能力和周围人员密度影响，针对人员不同运动能力，赋予相应的无障碍情况下的运动速度Ve。人员疏散运动速度随邻域内人员密度D(邻域内人员占比，即被主体占据的元胞数量与邻域元胞总数量之比)的增加而降低，人员密度过大时，运动速度接近于0，低密度情况下，人员间相互影响较小，规定该类人员以正常行走速度进行疏散。紧急情况下水平通道内人员行走速度V如式(4)所示[15]：

V=Ve×(1.49-0.36D)

(4)

应用式(4)计算模型中主体运动速度随邻域内人员密度变化情况，每一时刻各个主体运动速度受环境影响，可得到相应运动速度。

2.2 CA-Agent模型假定属性

1)疏散模型从众参数设定

疏散人员从众行为在模型中通过不同从众参数h(herding parameter)进行设置。从众倾向对应人员疏散的独立性与依赖性如图2所示。当h=0或h数值较小时，表示疏散人员情绪冷静，对危险情况有认知能力并且对环境较为熟悉，可依据自己的判断进行疏散，不受身边他人影响，此时人员从众倾向较低，对他人依赖性小，表现出独立的思考与判断，如图2中Ⅱ区域所示；当h=1或h数值较大时，表示疏散人员处于恐慌情绪中，对环境及疏散路线的判断完全依赖于他人，缺少自主认知和理性决策，此时人员从众倾向较强，独立性较弱，如图2中Ⅰ区域所示。从众参数h还可代表疏散中选择从众行为的人群比例，即疏散人群的从众程度。

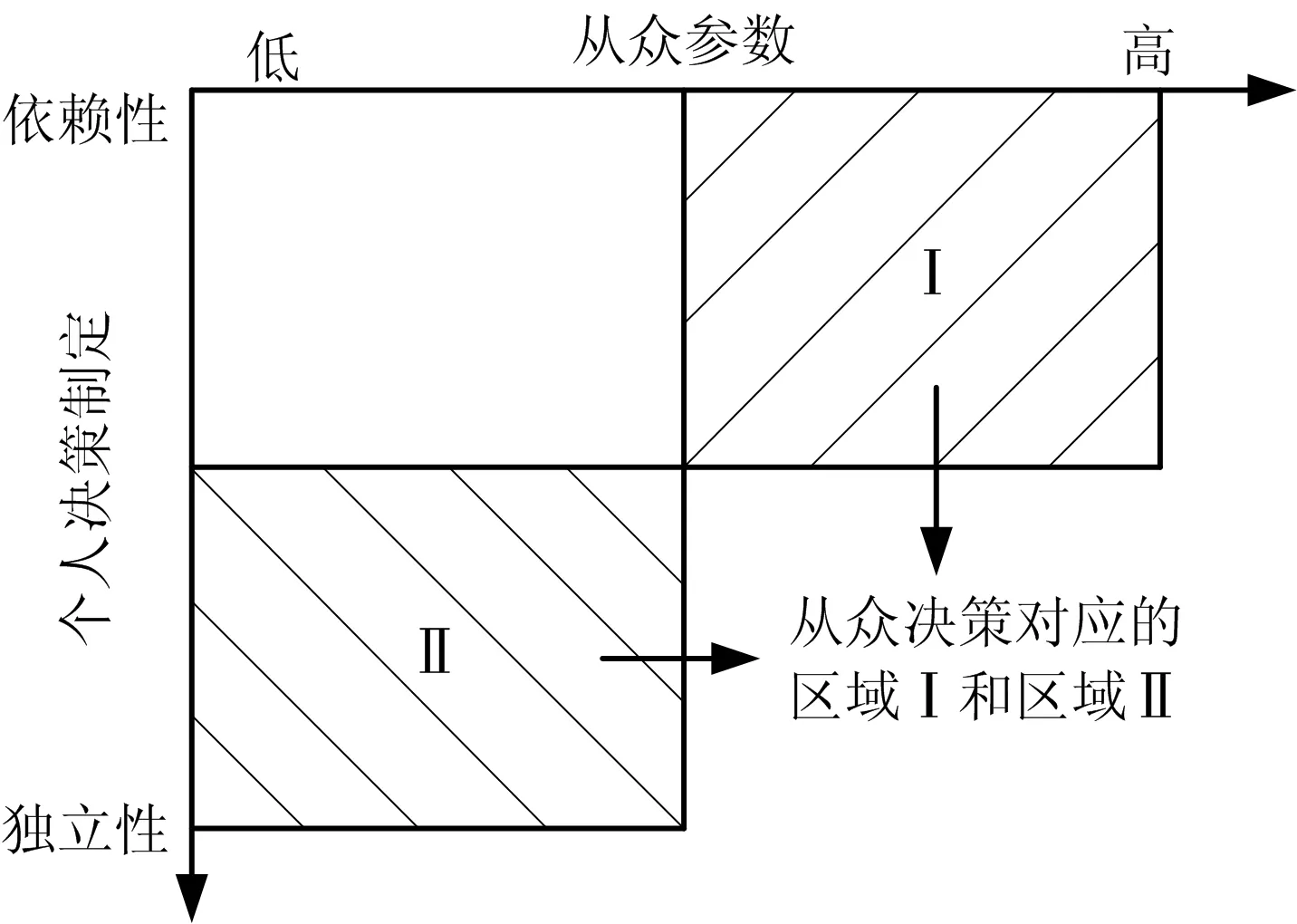
图2 从众倾向对应人员疏散的独立性与依赖性Fig.2 Herding tendency corresponding to independence and dependence of personnel evacuation

部分学者认为人群从众行为可提高疏散效率，缩短疏散时间，但部分学者认为人员会避免跟随人流运动而相信自身判断，同样可以提高疏散效率。因此，本文引入从众阈值的概念，研究人群疏散从众行为临界值。从众阈值指人群疏散效率达到最高时对应人群从众行为选择临界值，表示人群总疏散时间最短(tmin)时对应的从众参数数值(ht)。疏散过程中选择从众行为的人群比例达到从众阈值，则为人群疏散效率最大值点，即从众行为对人群疏散有益的最大人数比例。

2)疏散模型的主体速度设定

因人员身体状况、年龄等因素产生的运动能力差异是模型考虑的属性之一。在1个非特定人群中，人员组成多元化且随机性强，应考虑个体间运动能力差异，并分别对主体速度属性进行设定。学者针对人群分布与设计进行研究时得出，人员在公共场合水平道路中疏散时，运动速度范围为0.51～1.27 m/s；Proulx[16]通过公寓楼疏散实验测得人员平均疏散速度分别为1.05，0.95 m/s。设定主体疏散速度，选定运动速度区间为[0.5,1.5]，按照正态分布随机分配主体运动速度Ve。

2.3 模型疏散流程与算法解释

考虑从众阈值和主体特征的人群疏散元胞自动机模型算法流程如图3所示。人群疏散模型算法主要包括以下6个步骤：

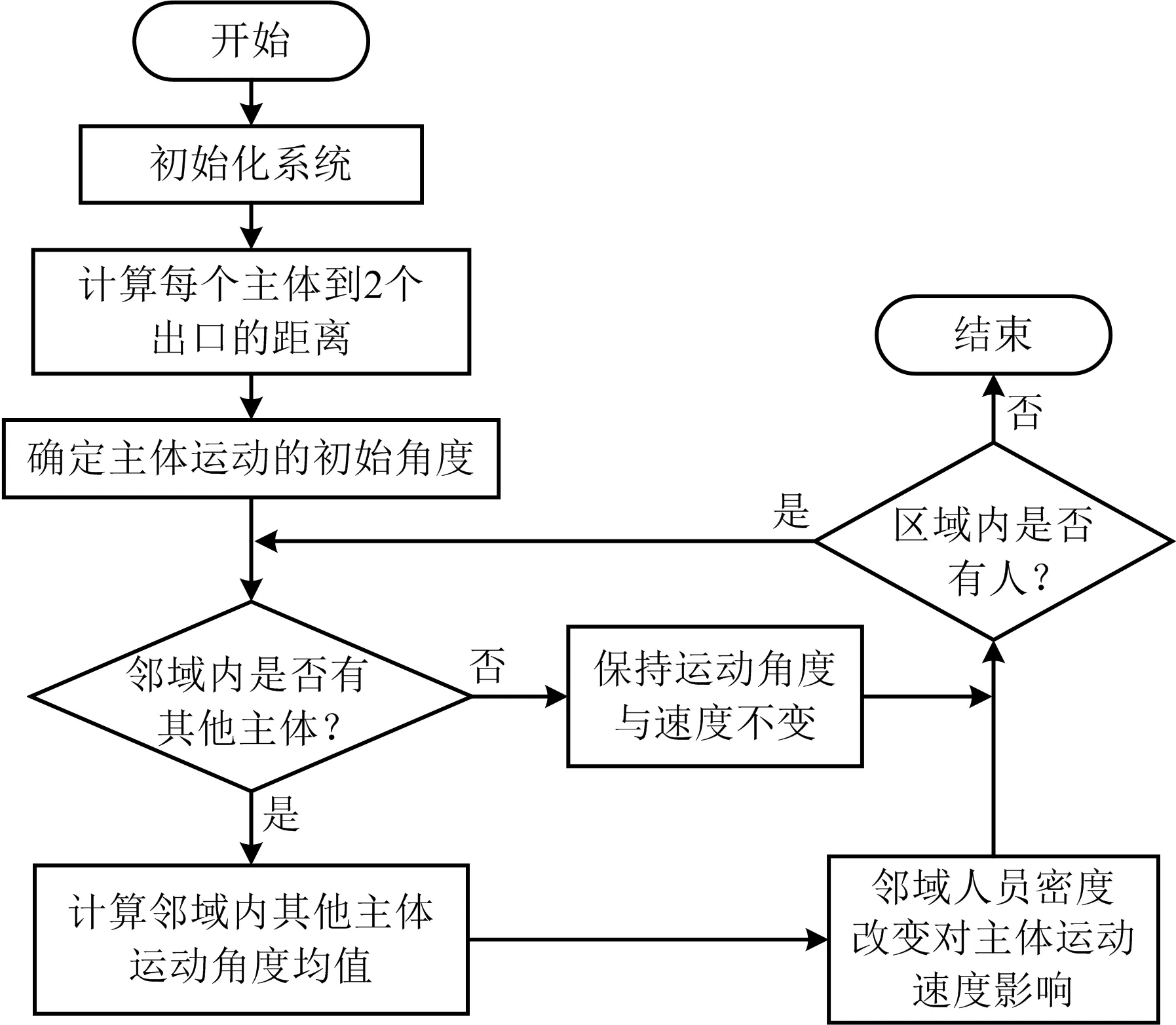
图3 人群疏散模型算法流程Fig.3 Flow chart of crowd evacuation model algorithm

1)初始化计算区域，初始化人员分布。

2)输入从众参数h，时间步0.05 s，设置出口宽度与位置坐标。

3)疏散区域内人员组成集合C={A1,A2,A3,…,A40}。

4)计算主体到2个出口的距离作为选择判据(当与2出口距离相同时，设置随机选择出口)，并以到该出口的角度为初始运动方向。

5)对每个主体判断其邻域内是否有其他主体：若是，则计算邻域内主体运动角度均值，与该主体原运动角度根据公式计算得到下一时刻主体运动角度，并根据邻域内人员密度计算下一时刻主体运动速度；若否，则该主体下一时刻保持原运动角度与速度不变。

6)判断疏散区域内集合C是否还有主体组成：若是，则说明区域内人员未疏散完毕，循环以上计算步骤；若否，则集合C为空集，说明区域内人员已全部疏散完毕，结束运行。

3 人群疏散过程的数值计算与结果分析

3.1 疏散场景与参数设置

应用疏散模型对单一空间人群疏散进行模拟研究。疏散场景为20 m×10 m的矩形空间，内共设2个出口，均位于矩形的同侧长边，双出口疏散区域初始状态主体分布如图4所示。首先令疏散人员随机分布于房间内，人员分别选择出口进行疏散；每次计算人员初始状态分布情况均不同(同组计算保持初始分布相同)，以房间内没有疏散人员为疏散结束的判断依据。

图4 双出口疏散区域初始状态主体分布Fig.4 Distribution of main body in initial state of double-exit evacuation area

3.2 结果分析

1)模型计算结果分析

应用疏散模型进行10组数值计算，每组包含11个数据(分别由h=0,0.1,…,1)。10组数据分别为人群在疏散区域的不同初始分布组成，因初始分布对疏散时间存在一定影响，计算虽不能涵盖所有可能结果，但仍认定具有参考价值。

通过研究可知，改变从众参数数值大小，人群的总疏散时间会随之发生变化，从众参数与疏散时间数值计算均值方差如图5所示。由图5可知，疏散时间均值范围为[22.98,24.58]，均值折线呈先递减后递增的趋势(呈V字型)，说明人群疏散时间随从众参数值的增大先降低后上升，当从众参数值较小或较大时，人群疏散所用时间较多，疏散效率不佳，存在使人群疏散时间最短、疏散效率最大的从众参数值，即为该种工况下的人群疏散从众阈值。

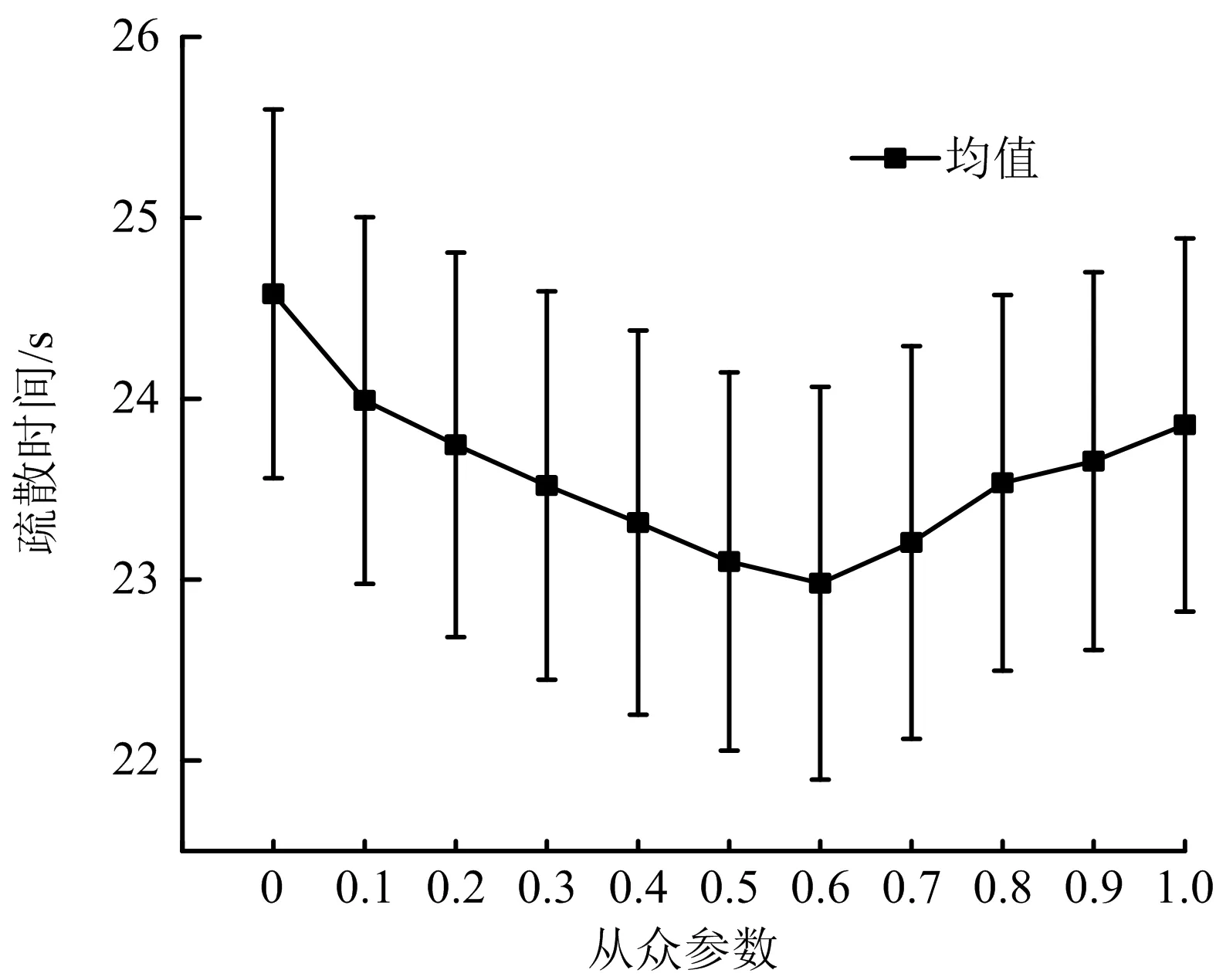
图5 从众参数与疏散时间数值计算均值方差Fig.5 Mean-variance of numerical calculation of herding parameter and evacuation time

由图5可知，从众参数h=0.6时，疏散时间均值达到最小值22.98 s，从众参数在[0,1]取值范围内存在可使疏散时间达到最小值的从众阈值。应用构建的疏散模型计算可知，当从众参数h=0.6时，人群疏散时间达到最小值，即在该工况下的从众阈值为0.6，人群中具有从众倾向的人员占比约为60%，人群疏散效率最优化。该从众阈值仅针对提出的疏散模型及相关工况，实际应用需针对情况进行分析参考。

对计算得到的疏散时间数据进行核密度估计(Kernel Density Estimation)，当采用Gaussian核函数和默认最优窗宽时，核密度估计与分布密度函数如图6所示。

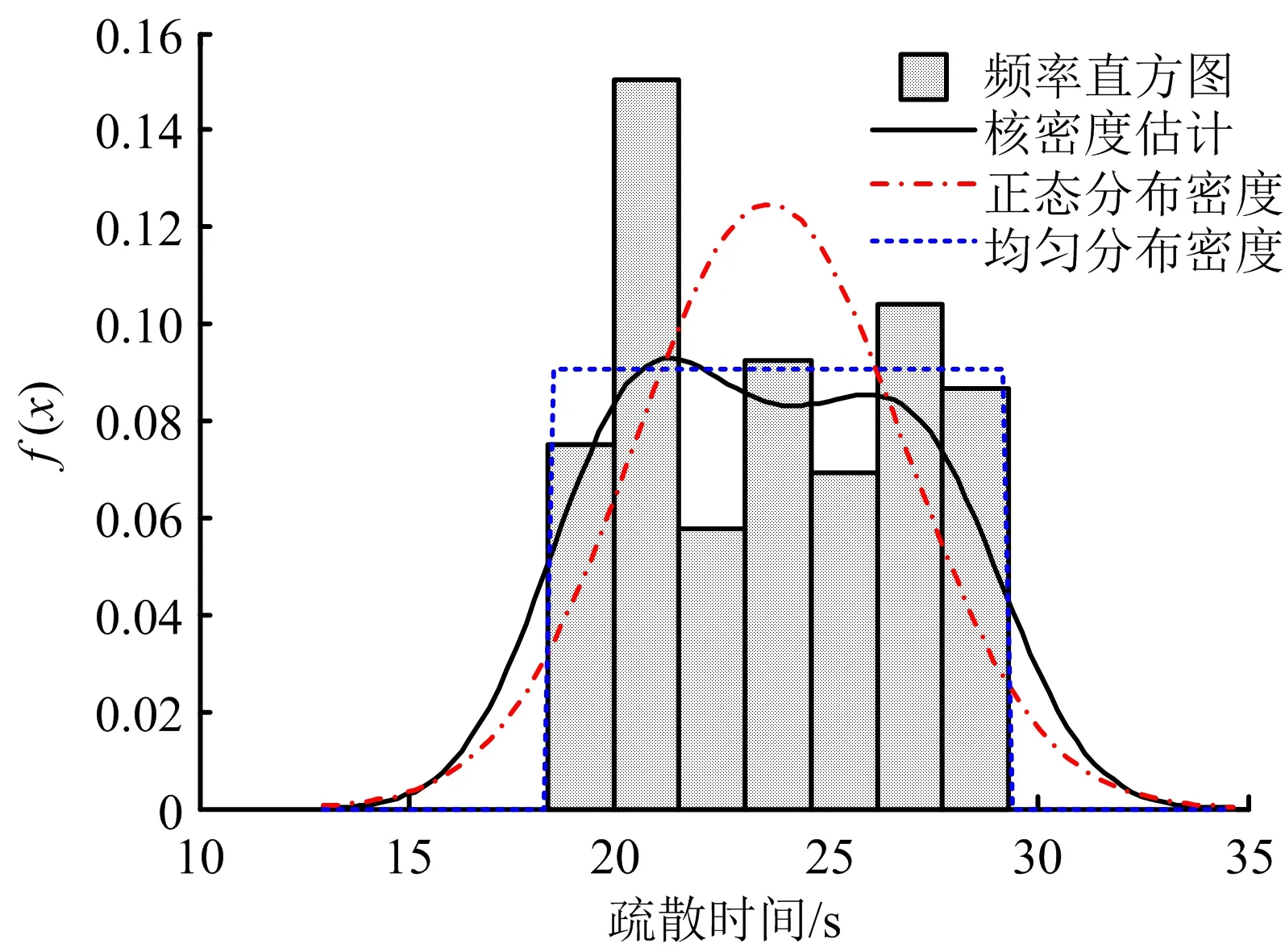
图6 核密度估计与分布密度函数Fig.6 Kernel density estimation and distribution density function graph

由图6可知，当核密度估计的窗宽为1.778 8时，用Gaussian核函数得到的核密度曲线为双峰曲线，峰值出现在21.0，26.0 s 2个时间点附近，说明人群总疏散时间多集中于这2个时间点。核密度曲线与Normal(23.592 3,3.198 32)分布的密度函数进行对比，符合度不够理想，与区间在[18.3,29.3]的均匀分布函数对比，符合度较低。核函数曲线与疏散时间频率直方图(7个小区间)符合度较好，而正态分布密度曲线和均匀分布密度曲线与疏散时间频率直方图符合度不够理想。

2)不同工况下从众参数与疏散时间关系

通过改变疏散条件研究不同工况下从众参数与疏散时间的关系，得到不同工况下人群疏散从众阈值并进行比较，如图7所示。由图7可知，共包括4组模拟人数工况，分别为30、40、50、60人，4组工况下疏散时间的变化规律大体相同，均呈先减小后增加的变化趋势，当从众参数较小或较大时对应疏散时间较大，而不同人数组存在不同的从众阈值(4组工况的从众阈值分别为h=0.5和h=0.6)，其对应疏散时间值达到最小，疏散效率达到最大化。

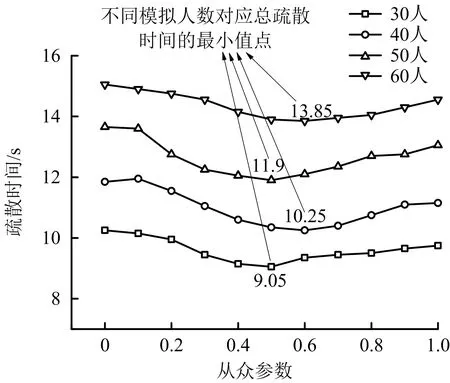
图7 不同模拟人数情况下从众参数与疏散时间对应关系Fig.7 Corresponding relationship between herding parameter and evacuation time under different numbers of personnel

不同双出口间距工况下人群疏散从众参数与疏散时间对应关系如图8所示。由图8可知，共包含3种双出口间距情况：出口坐标(2,10)和(18,10)，间距16 m；出口坐标(5,10)和(15,10)，间距10 m；出口坐标(8,10)和(12,10)，间距4 m。不同双出口间距情况下，疏散时间随从众参数变化趋势相似，呈先减小后增加的变化趋势，当从众参数较小或较大时对应疏散时间较大，而不同双出口间距情况存在不同的从众阈值(3组数据的从众阈值分别为h=0.5和h=0.6)，其对应疏散时间值达到最小，疏散效率最大化。

图8 不同双出口间距情况下从众参数与疏散时间对应关系Fig.8 Corresponding relationship between herding parameter and evacuation time under different distances of double-exit

将不同工况下的疏散模拟与原始工况进行比较发现，人群疏散从众参数与总疏散时间对应的变化规律基本一致，均呈先减小后增大的变化趋势，存在疏散时间最小的对应从众阈值点。与原始工况不同的是，在改变人数与改变出口间距工况下，从众阈值发生变化，存在h=0.5和h=0.6 2个不同的数值，说明工况不同将对从众阈值产生影响，从众阈值可能受疏散人数、出口间距、出口位置、环境能见度、烟气浓度等多种因素影响，还需进一步开展更深入全面的研究。

4 结论

1)建立基于主体与元胞自动机的人群疏散模型，结合2者优点，不仅能通过元胞自动机模拟系统运动状况及整体的动态演化，还能兼顾每个主体的不同特征属性，考虑不同人员认知能力导致的疏散从众选择差异。

2)提出从众参数h，并对模型中疏散人员的从众行为进行设置，引入从众阈值概念对人群行为进行研究，并研究人群疏散从众行为临界值。对从众行为的程度进行量化，计算最有利疏散的临界值，对人群疏散研究具有现实指导意义。

3)对数值计算结果进行核密度估计，讨论从众参数h与疏散时间t的关系，确定本模型原始工况下的计算结果，当从众参数为0.6时疏散时间最短，即当人群中约60%的人员在疏散中表现出从众趋向，整体疏散效率得到优化。