突发公共卫生事件下多阶段应急救援物资配置研究*

段容谷，庄媛媛，张克勇，吴云霞

(中北大学 经济与管理学院，山西 太原 030051)

0 引言

过去十几年中，在全球范围内爆发了多种公共卫生事件，对人类生命安全与财产造成了巨大损失。重大公共卫生事件爆发背景下，应急救援物资数量庞大，种类繁多，在有限的人力、物力资源与时间限制下，对应急物资进行分类和分配是一项十分困难的任务。面对不断变化的需求与供给能力，应急物流发挥着举足轻重的作用。因此，完善应急物流分配方案，提升应急物流物资分配效率势在必行。

国内外有关应急物流物资分配的研究主要集中于物资分配目标选择及优化模型构建[1-5]、多阶段物资分配[6-8]与需求的不确定性相关问题[9-10]。李旭东等[11]剖析了应急物流运行中存在的物流效率低、物资保障混乱等问题。也有一些学者涉及了应急救援的需求紧迫度分级的相关研究。Wang等[12]研究了在紧急状态下按照等级对应急物资分配的问题；张毅[13]指出应急物资种类繁多，应急物资分配存在优先级；Jiang等[14]建立模型，根据供电特性评估了受影响区域的分配优先级。此外，贺俊杰等[15]研究了1个需求点和多个供应点的消防应急物资配置最优化研究问题；Haghi等[16]提出了存在灾前与灾后预算约束条件下的物资分配问题。Wang等[17]研究了灾后医疗救援队伍的派遣和救援物资在需求点之间的分配问题。

在重大公共卫生事件爆发初期，应急物资通常会出现供应短缺，且救援物资需求量与供给量呈现动态变化。因此，需要通过不同阶段多个周期来满足救援物资的需求。而国内外学者对公共卫生事件背景下多阶段应急物资配置研究尚有不足，多数未考虑对救援物资的管理问题。而在突发公共卫生事件爆发后，大量来自于其他地区的捐赠、调拨、补货物资需要花费人力与时间对其进行分类、检验。因此，本文提出在公共卫生事件背景下，以应急物资分配中需求未满足所导致的损失最小及分配距离最短为目标，以分配能力等因素为约束，构建多阶段应急物流物资分配模型进行多阶段、多渠道物资管理研究。以期能够为应急物资快速、精准分配提供依据。

1 研究问题描述及基本假设

重大公共卫生事件爆发后，为在应急物资供给能力不断变化条件下实施精准快速救援。将救援过程根据不同分配方式分为2个阶段，在对需求点进行需求紧迫性评价后统筹安排应急物资分配。

第1阶段分配为属地一次分配，能够实现应急物资的快速分配。具体描述为：某一地区有M个需求点，N个属地供应点，爆发重大公共卫生事件后，将供应点中有限的应急物资分配至需求点。其应急物资分配结构如图1所示。

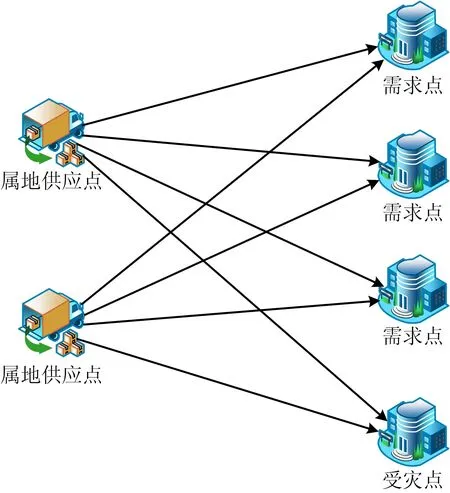
图1 属地供应点-需求点网络拓扑结构Fig.1 Topological structure of territorial supply point-demand point network

第2阶段分配为包括外埠供应点、配送中心、受灾点的3级供应链动态应急物资分配。基于第1阶段分配后数据被更新的基础，能够应对物资需求量及供给能力随疫情发展的不断变化。此阶段外埠供应点作为分配的供应点，属地供应点作为应急物资分配中心，实施应急救援物资的分配。具体描述为：将外埠供应点的应急物资经过属地供应点分配至各需求点。为保证外埠供应点的供应量不断得到补充，各外埠供应点均有相应的供应商及生产商为其补货。同时，社会各界捐赠的应急物资也将不断送达属地供应点以分配到各需求点。应急物资第2阶段分配的网络拓扑结构如图2所示。

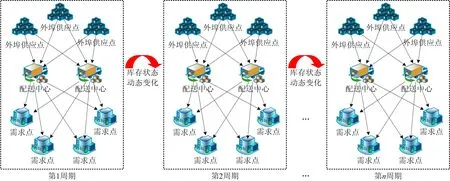
图2 第2阶段外埠供应点-配送中心-需求点网络拓扑结构Fig.2 Topological structure of out-port supply point-distribution centre-demand point network in second stage

2 模型建立

2.1 模型假设

结合公共卫生事件下应急物资分配的实际情景，做如下假设：

1)己知各阶段各需求点的需求量及受灾程度、供应点可供应量、外埠供应点与属地供应点及需求点之间的距离等信息。

2)不同种类物资可以使用同一种分配优化方法。因此，本文构建单一种类应急物资分配模型。

3)考虑到公共卫生事件爆发对城市交通并无直接负面影响，假设外埠供应点、属地供应点、需求点之间的道路畅通，运输车辆充足。

4)供应点储存空间均充足，但由于平时工作量远不及公共卫生事件爆发时大，专业分拣工作人员、装卸分拣设备有限。公共卫生事件爆发后易出现物资管理专业人手、物流作业设备不足的情况。采购物流设备、培训志愿者均需要一段时间。因此，假设公共卫生事件应急救援过程中存在分配能力约束。经过志愿者培训、采购调用物流设备等措施后，分配能力逐渐满足需求。

5)以1 d(24 h)为1个周期分配物资。

2.2 模型构建

现有应急物资分配的相关研究中，通常只假设目标函数为线性函数，采用求取各需求点需求未满足损失率的加权和来进行计算[18]。而考虑到由于应急物资需求未满足所导致的损失通常与物资短缺量呈正相关凸函数关系。因此，本文引入指数效用函数量化由于物资短缺而产生的损失[19],如式(1)：

Pi[δi]=[1-e-α·δi]/αα<0

(1)

式中：Pi为需求点i因应急物资短缺所造成的损失函数；α为常数；δi为需求点i对于应急物资的短缺程度，表示为式(2)：

(2)

式中：Qi为需求点i的需求量；xji为属地供应点j分配到需求点i的物资量；ωi为需求点i的需求紧迫程度。

2.2.1 第1阶段物资分配模型建立

在充分收集、分析公共卫生事件爆发后供需信息的前提下，构建应急物资一次分配的模型，使各需求点应急物资缺货损失及分配距离最小。

1)目标函数如式(3)～(4)：

(3)

(4)

式中:dji为属地供应点j到某一需求点i的距离；目标函数式(3)，(4)分别表示最小化所有需求点应急物资缺货损失与分配距离。

2)约束条件如式(5)～(9)：

(5)

(6)

(7)

(8)

xji≥0 ∀i∈I,j∈J

(9)

式中：Sj为属地供应点j的应急物资储备量；θ为各需求点所需获得的最低满足率；Ej为属地供应点j的最大发货能力。

式(5)表示从所有属地供应点分配给需求点i的应急物资不大于其需求之和；式(6)表示从属地供应点j分配给所有需求点的应急物资之和不大于其可供给量；式(7)表示各需求点i获取应急物资的满足率不低于其最低满足率；式(8)表示从各属地供应点j分配给所有受灾点的应急物资之和，不大于其最大分配能力Ej；式(9)表示决策变量为非负。

2.2.2 第2阶段物资分配模型建立

1)目标函数如式(10)～(13)：

(10)

(11)

(12)

(13)

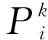
目标函数式(10)，(13)分别表示最小化所有周期所有需求点应急物资缺货损失与分配距离；式(11)表示k周期需求点i应急物资的缺货损失函数；式(12)表示k周期需求点i应急物资短缺量。

2)约束条件如式(14)～(20)：

(14)

(15)

(16)

(17)

(18)

(19)

(20)

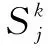
3 模型求解

本文对模型的求解主要分为3个步骤:首先使用TOPSIS法评价各需求点对应急物资的需求紧迫程度；其次本文所构建的优化模型为非线性规划问题，为降低问题计算复杂度，采用线性近似法将非线性目标函数转化为线性目标函数[20]，采用遗传算法求解主要目标函数；最后，在主要目标函数取得最优方案的条件下采用运输单纯形法求解次要目标函数。现有多目标优化问题的相关研究多数采用将多目标转换为单目标函数求解模型，而在本文中，由于2个目标函数为主要目标与次要目标的关系，因此,采用先实现主要目标函数最优，再对次要目标函数实行优化求解，更加符合物资分配现实。

3.1 TOPSIS法

基本过程为：

1)将原始数据矩阵统一指标类型得到正向化的矩阵。

2)对正向化的矩阵进行标准化处理。

3)找到有限方案中的最优方案和最劣方案。

4)分别计算各评价对象与最优、最劣方案间的距离。

5)获得各评价对象与最优方案的相对接近程度。

运用MATLAB2014b进行求解，其计算结果作为各需求点对应急物资需求紧迫度评价信息。

3.2 线性近似法

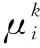
(21)

(22)

3.3 运输单纯性法

基本步骤：

1)寻找初始基本可行解(初始调运方案)。

2)求检验数并判断是否得到最优解，假设目标函数取最小，当非基变量的检验数全部非负时得到最优解。若存在检验数小于0，说明还未达到最优，转到3)。

3)调整运量，即换基。选1个变量出基，对原运量进行调整得到新的基本可行解，转到2)。

运用MATLAB2014b进行编程求解。

4 案例分析

4.1 案例描述

2020年爆发了新型冠状病毒肺炎，世界遭遇了防控难度最大的重大突发公共卫生事件。为实现应急物资的合理分配，本文以某市应急物资分配为例进行优化研究。假设该市共有13个需求点，2个属地供应点即配送中心，6个可以提供应急救援物资的外埠供应点。选取疫情爆发后2个阶段及第2阶段中3个需求供给变化典型周期作为研究对象，以防护服分配为例对其进行分配优化研究。并对分配后的结果进行分析，验证本文构建分配模型的科学性与可行性。选取需求点应急物资需求紧迫度评价的指标为如下3个因素：受灾人数、人口密度、患病人数。由于各需求点的需求紧迫度随疫情发展不断发生变化，因此，收集疫情每阶段的原始样本，见表1。

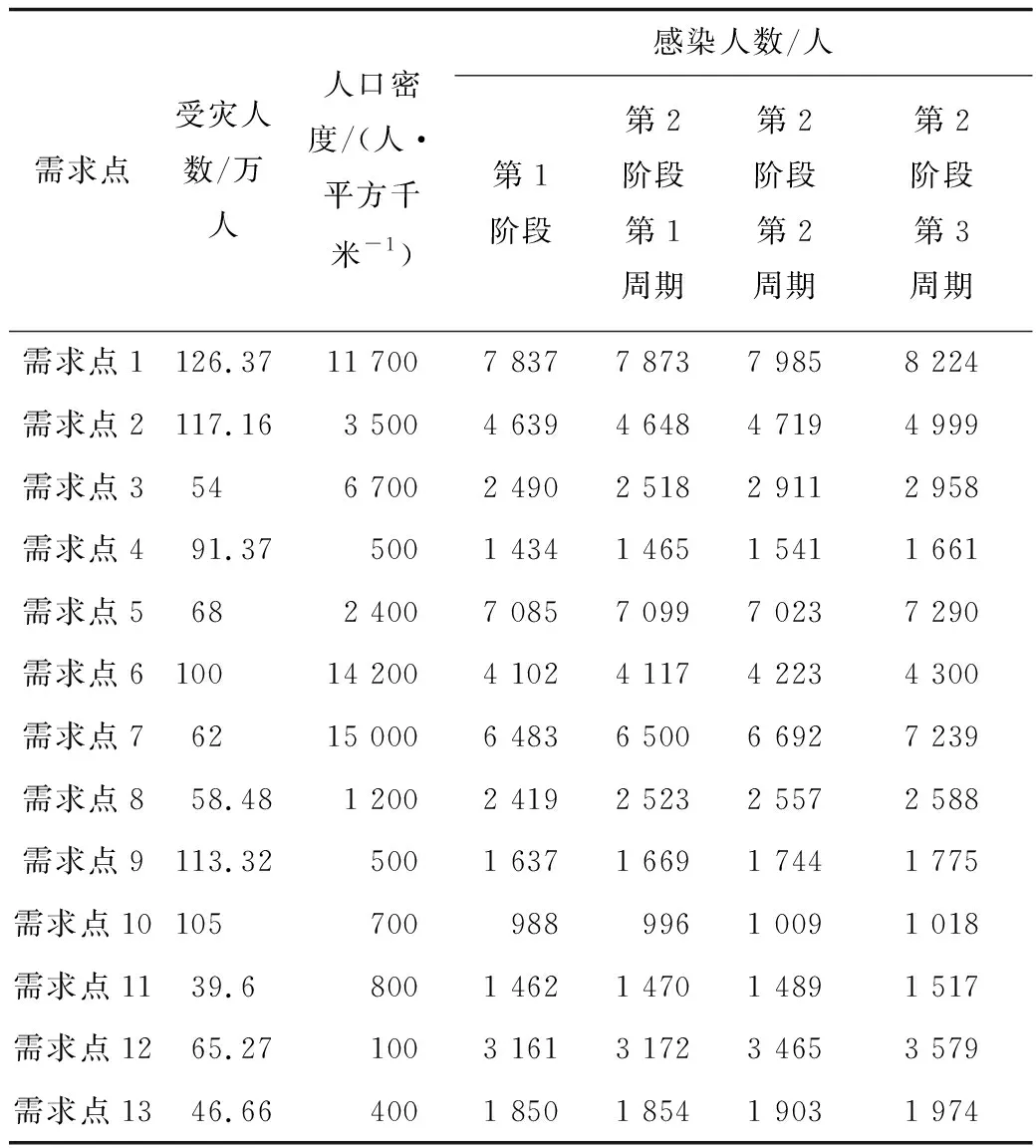
表1 各应急物资需求点紧迫性分级的指标数据Table 1 Index data of urgency classification for emergency supplies demand points

现已知13个需求点各阶段各周期应急物资的需求量与属地供应点到受灾点之间的距离，见表2。各外埠供应点、捐赠物资及属地生产物资配送至配送中心数量与距离见表3。其中假设捐赠物资全部直接由集散地运往配送中心1，属地生产物资直接从集散点运往配送中心2，M为极大值。

表2 各需求点需求量及属地供应点配送距离Table 2 Demand quantity of each demand point and distribution distances of territorial supply points

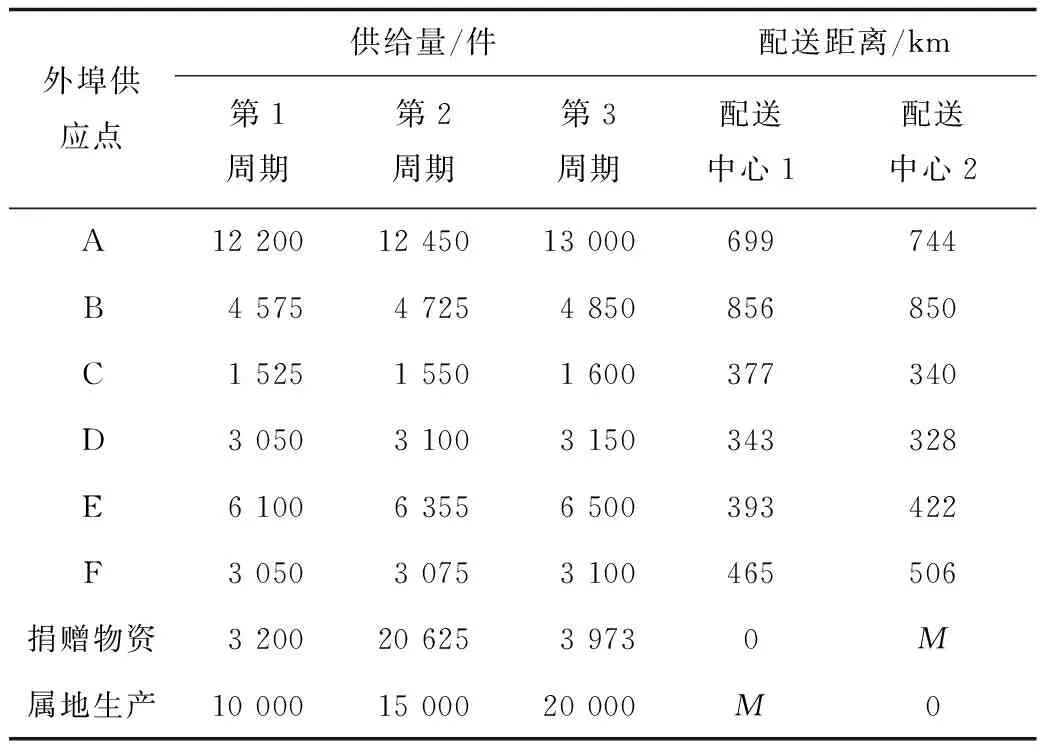
表3 第2阶段外埠供应点供给量及捐赠与属地生产量Table 3 Supply quantities of out-port supply points and donation and territorial production quantities in second stage

2个属地供应点对应急物资在第1阶段的可提供量分别为11 000，8 500，最大分拣配送数量均为10 000；在第2阶段各周期最大分配数量分别为20 000，25 000，35 000。第1阶段应急物资最低满足率为10%，第2阶段各周期分别为60%，70%，90%。

4.2 算例结果

通过Matlab2014b软件实现算例结果。基于表1中的相关数据，使用TOPSIS法评价出武汉市各区对应急救援物资的需求紧迫度。由于所模拟各时间段需求紧迫度评价结果近似，各阶段各周期需求点的需求紧迫度在此算例中赋值相同。因此，武汉市各区对应急救援物资的需求紧迫度由高到低的排序依次为需求点1、需求点7、需求点6、需求点5、需求点2、需求点3、需求点9、需求点10、需求点12、需求点4、需求点8、需求点13、需求点11。赋值分别为10，9，8，6，5，4.5，4，3.5，3，2.5，2，1.5，1。

使用遗传算法与运输单纯形法计算第1阶段属地一次分配与第2阶段3级供应链动态分配各周期结果，取α=-0.001。结果见表4～6。

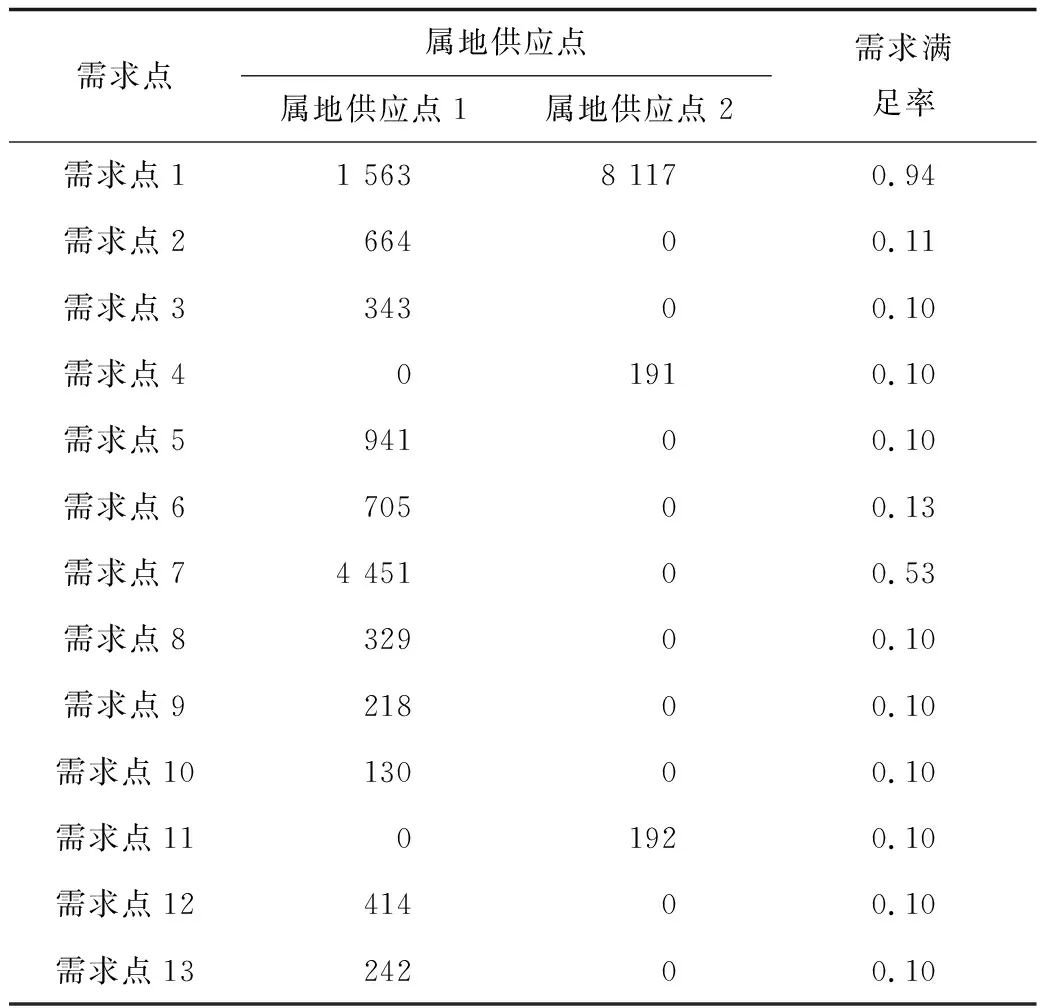
表4 第1阶段各属地供应点向需求点分配物资情况Table 4 Distribution of materials from each territorial supply point to demand points in first stage

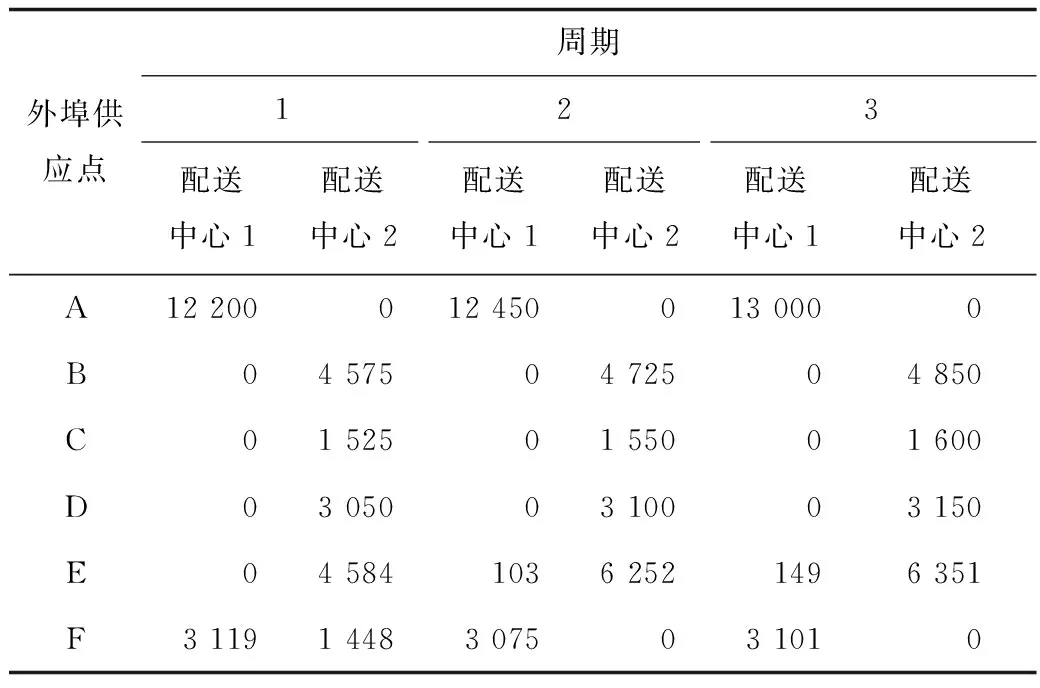
表5 第2阶段各周期外埠供应点分配至配送中心数量Table 5 Distribution quantities from out-port supply points to distribution centers in each cycle of second stage

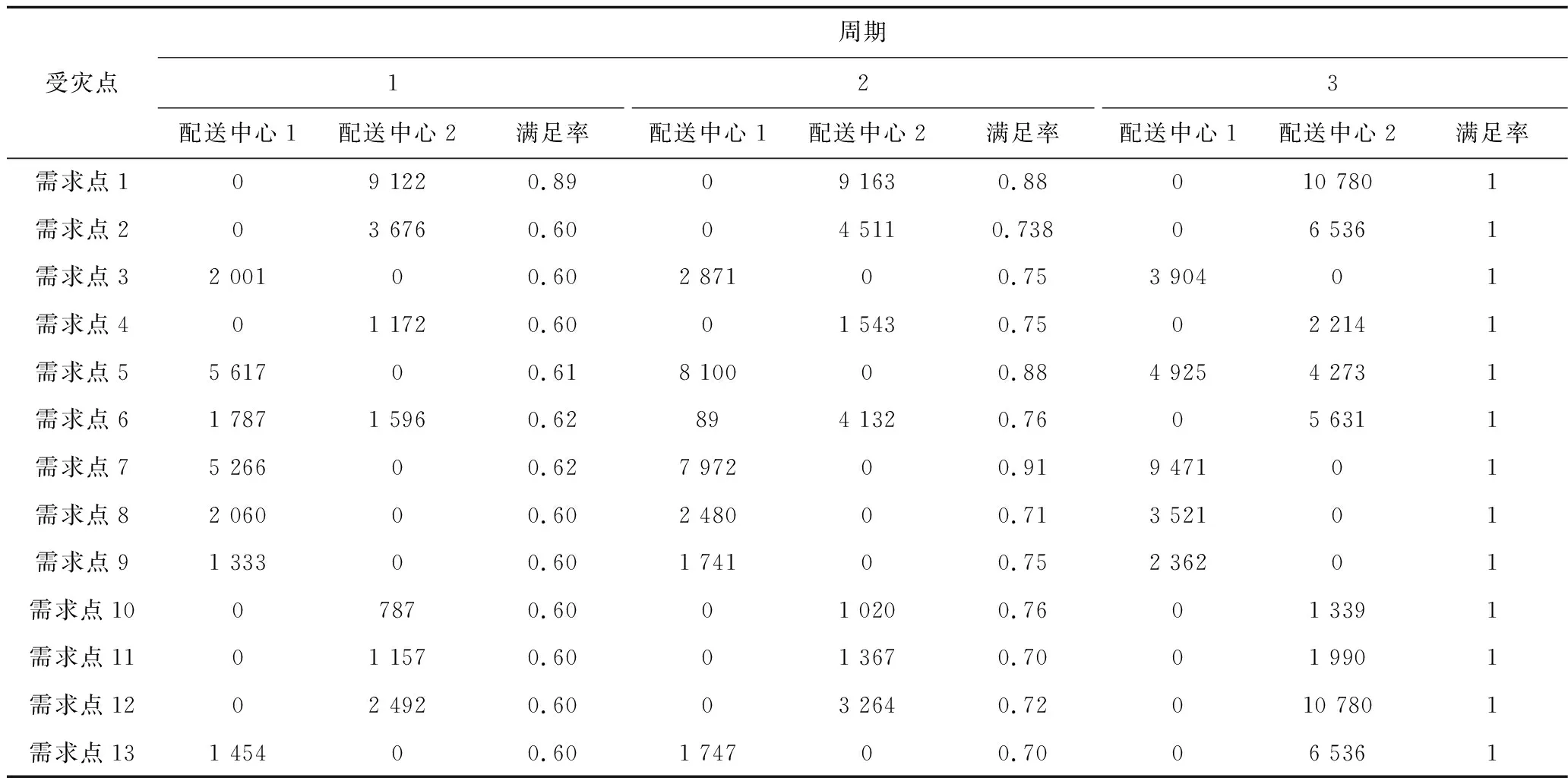
表6 第2阶段各周期各配送中心物资分配至受灾点数量Table 6 Distribution quantities of materials from each distribution center to disaster points in each cycle of second stage

从分配结果可见，本文所提出的模型能够尽可能地提高需求点对物资需求的满足率，进而降低各阶段需求点缺货损失；同时保证了分配的公平性(如表4中第1阶段所有需求点在供给远小于需求的情况下，其满足率均大于0.10,其中需求紧迫度最高的武昌区满足率最高，达到0.94)；该应急救援分配模型具有效率性，分配过程为首先将属地供应点的物资进行一次分配，同时调拨其他地区物资实施第2阶段物资分配，通过如上2个分配阶段在满足就近分配原则的条件下进行物资分配。如属地供应点A距离配送中心1与配送中心2的距离分别为699 km与744 km，则属地供应点A将应急物资运输至距离较短的配送中心1。根据以上算例结果可见，本文所提出的突发公共卫生事件下多阶段应急救援物资分配模型兼顾了物资分配的公平与效率。

结合本文研究与突发公共卫生事件下实际应急物资分配，为提高疫情防控应急物资的保障能力，可以采取以下举措：

1)面对突发公共卫生事件中存在的应急物资在入库、分拣、检测、分配、出库等过程中面临的人力资源与设施设备不足的情况，相关管理部门在储备应急物资之外还应储备一定运输装卸设备，并制定检测、分拣、装卸等人员上岗培训规范，以期在灾害爆发时能够快速招募志愿者上岗采取防控措施。

2)本文研究在基于可快速获取需求信息与供给信息的假设下完成，因此，建立良好的信息平台至关重要。只有快速准确的获取需求、供给及各灾害情况等信息才能精准地采取救援措施。

5 结论

1)为提高物资分配过程中的公平性，将各需求点对应急物资需求紧迫度进行评价，为应急物资分配提供参考条件。

2)突发公共卫生事件发生初期，分配调拨、捐赠、补充生产等渠道提供的应急物资在入库、分拣、检测、分配、出库等过程中面临的人力资源与物流设备不足的情况。因此，将人力资源与物流设备的限制列为应急物流物资分配的约束条件。

3)需求点对应急物资需求的紧迫性及需求量与供给能力随疫情发展趋势的变化而波动。因此，分别建立应急物资分配初期属地供应一次分配模型，与中前期多外埠供应点、多配送中心、多需求点、多周期的3级供应量动态物资分配模型。

4)模型考虑了政府调拨、物资捐赠、供应商与生产商补充多种供应渠道，使本文研究更具有实际应用意义。