基于蒙特卡洛方法的油气井管柱可靠性评估*

张认认，杨尚谕，王建军，赵 楠，徐长峰，李新宏

(1.西安建筑科技大学 资源工程学院，陕西 西安 710055；2.中国石油集团工程材料研究院有限公司 石油管材及装备材料服役行为与结构安全国家重点实验室，陕西 西安 710077；3.中国石油新疆油田分公司呼图壁储气库作业区，新疆 呼图壁 831200)

0 引言

管柱完整性是保障气井工作的先决条件，管柱失效会引发井筒泄漏、停产等严重后果[1]。为了降低超深油气井的生产风险，开展其井筒管柱的可靠性评估显得尤为重要。许亮斌等[2]应用非概率可靠性理论研究变量的不确定性，并计算实际载荷作用下套管的可靠度；赵垒等[3]应用区间模型构建了套管的可靠性模型，计算不同服役阶段套管的可靠性；樊恒等[4]基于分项系数法提出了套管在钻完井和生产阶段的强度可靠度设计方法，分析荷载和强度的变异系数对套管可靠性设计的影响；许志倩等[5]对特殊螺纹接头进行仿真模拟，分析了特殊螺纹接头的应力分布及其实际载荷下螺纹接头的可靠性；LIAO和LONG等[6-7]进行了油气井安全分析，评估了非均匀外载下套管的可靠性；Zhu等[8-9]提出1种基于贝叶斯优化理论的储气库管柱可靠性分析方法，计算管柱抗挤强度；上述研究提出了不同可靠性分析方法及模型，但多采用经验和假设方法确定可靠性模型变量的概率分布，从而对可靠性评估结果产生一定的不确定性。

为了更加准确地评估油气井管柱的可靠性，对影响管柱可靠性的影响因素进行数据统计与分析，并结合蒙特卡洛方法对管柱剩余强度进行计算，以提高管柱可靠性评估的准确性。蒙特卡洛方法是一种传统但准确的可靠度分析方法，且易于与其他可靠性评估方法相结合。Fu等[10]基于蒙特卡洛法提出了二阶可靠性评估方法，并对集成能源系统的失效概率进行了评估；Wang等[11]提出了一种基于哈密顿蒙特卡洛的可靠性评估方法。

基于对外载的数据统计分析，结合理论模型和蒙特卡洛模拟对苛刻油气井管柱进行可靠性评估，并以某油气井为例对管柱可靠性进行分析。首先，确定影响管柱可靠性的2类随机变量，采用极限状态方法构建管柱可靠性理论模型；然后，对外载变量进行数据统计，分析变量的分布规律与参数；最后，结合蒙特卡洛方法构建管柱可靠性数值模型。

1 构建管柱可靠性模型

影响管柱状态的变量xi可分为2大类，第一类是影响管柱外部载荷的随机变量L，第2类是影响套管强度的随机变量S，2类变量的函数表达式如式(1)所示：

(1)

式中：xLi为与套管载荷有关的随机变量；xSi为与套管强度有关的随机变量。

将多个随机变量简化为两个随机变量进行计算，如式(2)所示：

Z=L-S

(2)

式中：Z为极限状态的功能函数。

假设强度和载荷是相互独立的2类随机变量，且服从一定的概率分布，其概率密度函数分别为pL(x)和pS(x)，则可得套管可靠度Pr的表达式，如式(3)所示：

Pr=P(Z>0)=P(S-L>0)

(3)

基于地层岩石力学和套管柱自身性能参数的概率分布，根据极限方程原理建立套管柱的可靠性模型，其变量包括岩石力学、水泥环和套管柱强度影响因素，如式(4)所示：

Z=g(S0,P,P1,P2,P3,E3,ν3,E2,ν2,D2,E1,ν1,D1,T)

(4)

式中：g为套管可靠性影响因素的函数;S0为P110套管抗屈服强度，MPa；P为钻完井阶段套管内压，MPa；P1为某深度地层最大水平主应力，MPa；P2为某深度地层最小水平主应力，MPa；P3为某深度地层的垂向平主应力，MPa；E3为某深度地层的弹性模量，G；ν3为某深度地层的泊松比；E2为水泥弹性模量，G；ν2为水泥环泊松比；D2为水泥环厚度，mm；E1为P110套管弹性模量，G；ν1为P110套管泊松比；D1为P110套管外径，mm；T为P110套管壁厚，mm；

Z大于零时套管的状态是安全的，其发生概率为套管柱的可靠度，记为Pr；Z小于零时套管的状态是不安全的，其Z发生概率为套管柱的失效概率，记为Pf，式中，p为套管极限状态的函数,如式(5)所示：

(5)

2 模型变量概率分布

以某气井为例，评估其井筒管柱的可靠性。通过地应力的统计与计算，取地层3个主应力分别为135.32 MPa、124.19 MPa和113.09 MPa；根据实际钻井液密度计算出管柱内压为79.62 MPa；根据API标准取套管外径为177.8 mm，壁厚为12.65 mm，屈服极限为828 MPa；根据工程实际取水泥环外径为241 mm，设置距井眼1 000 mm的地层厚度。

管柱安全状态主要受外界荷载和管柱抗挤能力的影响，其中外载变化主要受地质和水泥环的影响，抗毁强度主要受管柱自身参数影响。外载和抗挤能力具有不确定性和随机性，会在一定范围内波动变化。因此，需要对影响管柱安全的地质相关因素、水泥环相关因素和管柱自身因素进行数据统计与分析，确定其分布类型和参数。

参考现场数据和大量文献资料，对目标区域的岩石力学参数和地应力进行数据统计，得到弹性模量、岩石泊松比和地应力等数据，统计分析其变异系数、均值和标准差等，得到弹性模量和泊松比服从正态分布，经过拟合得岩石弹性模量和泊松比正态分布曲线方程为式(6)和(7)：

(6)

(7)

得到1.3～3.7 km区间内的地应力数据，包括最大水平地应力、最小水平地应力和地层垂向地应力均服从线性分布，分析可得：地层3向应力分布均符合实际地应力的分布，即相同深度下，威远-长宁区地应力关系为：最大水平地应力>垂向地应力>最小水平地应力。

水泥环是井筒构件的重要组成部分之一，是重要的水力屏障。水泥环的几何性能是指外径和厚度；力学性能是指弹性模量和泊松比。根据现场施工的数据，参考API中水泥环相关性能参数分布，可知水泥环的性能参数均符合正态分布，其分布参数见表1。

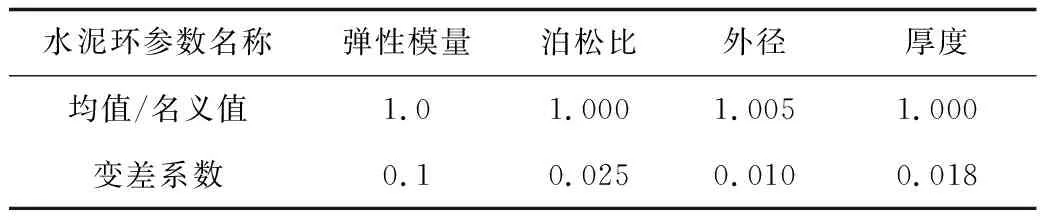
表1 水泥环相关变量及分布参数Table 1 Relevant variables and distribution parameters of cement sheath

管柱属性的随机性是影响其强度的关键参数，包括几何参数(如外径、壁厚)和力学参数(如弹性模量、泊松比、最小屈服强度)。由于受到制造、运输等原因造成的实际套管属性值并不等于名义绝对值，存在一定的偏差。据统计分析可知套管属性均服从正态分布，API套管性能的随机分布及参数见表2。

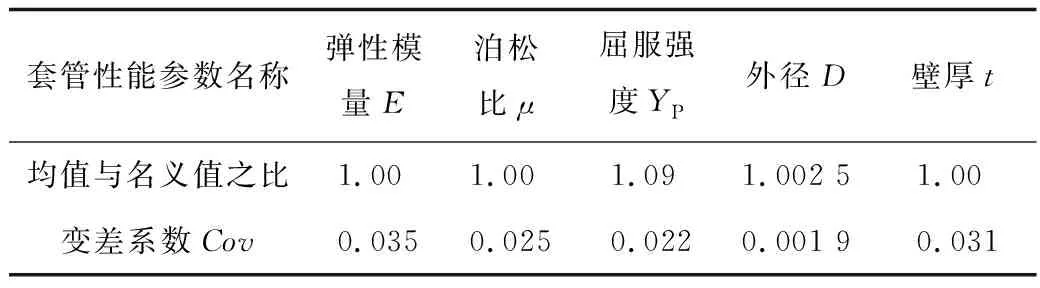
表2 套管性能变量参数随机分布Table 2 Random distribution of variables parameters about casing properties

3 油气井管柱可靠性评估

根据管柱可靠性模型，结合蒙特卡洛方法进行管柱剩余强度模拟，计算管柱的剩余强度及安全系数，评估6 000 m处油气井井筒管柱的可靠性。

管柱可靠度是指管柱实际承受的结构强度小于额定抗拉、抗压和抗挤强度，并满足其安全系数要求。根据美国石油协会API套管强度计算标准[12]，查表可知P110#套管的额定抗拉强度为52.54 MPa，安全设计系数为1.6～1.8；额定抗挤强度为94.423 MPa，安全设计系数为1～1.35；额定抗压强度为89.8 MPa，安全设计系数为1～1.125。参考API标准[12-13]和管柱强度设计资料，分别计算出1～7 km处套管柱的抗拉、抗内压和抗挤强度及安全系数，见表3。

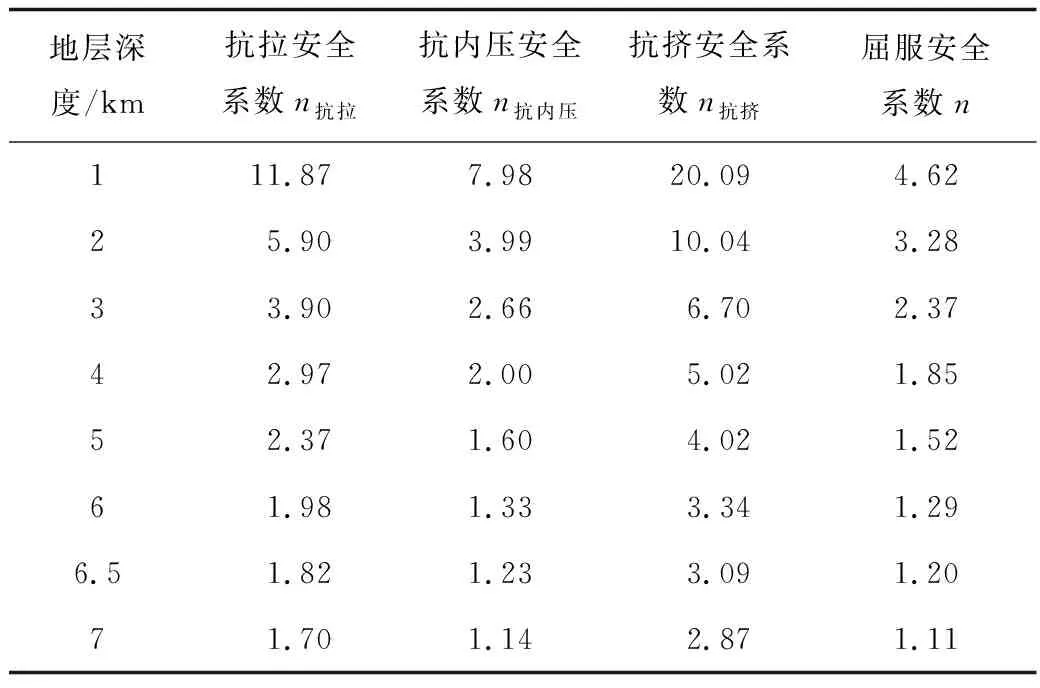
表3 不同深度下套管强度安全系数计算值Table 3 Calculated values of safety factor for casing strength at different depths

以API规定的套管安全系数[13]设计值为基础，同时考虑超深气井的钻采条件的苛刻性，设计套管柱抗挤安全系数n抗挤为1.125，设计抗拉安全系数n抗拉为1.80，设计抗内压安全系数n抗内压为1.20。由表3可知，满足套管强度安全系数的理论计算地深为6.5 km，并绘制安全系数变化曲线，如图1所示。分析可知，管柱的强度安全系数随地层深度增加而降低；且管柱抗挤安全系数n抗挤>抗拉安全系数n抗拉>抗内压安全系数n抗内压。

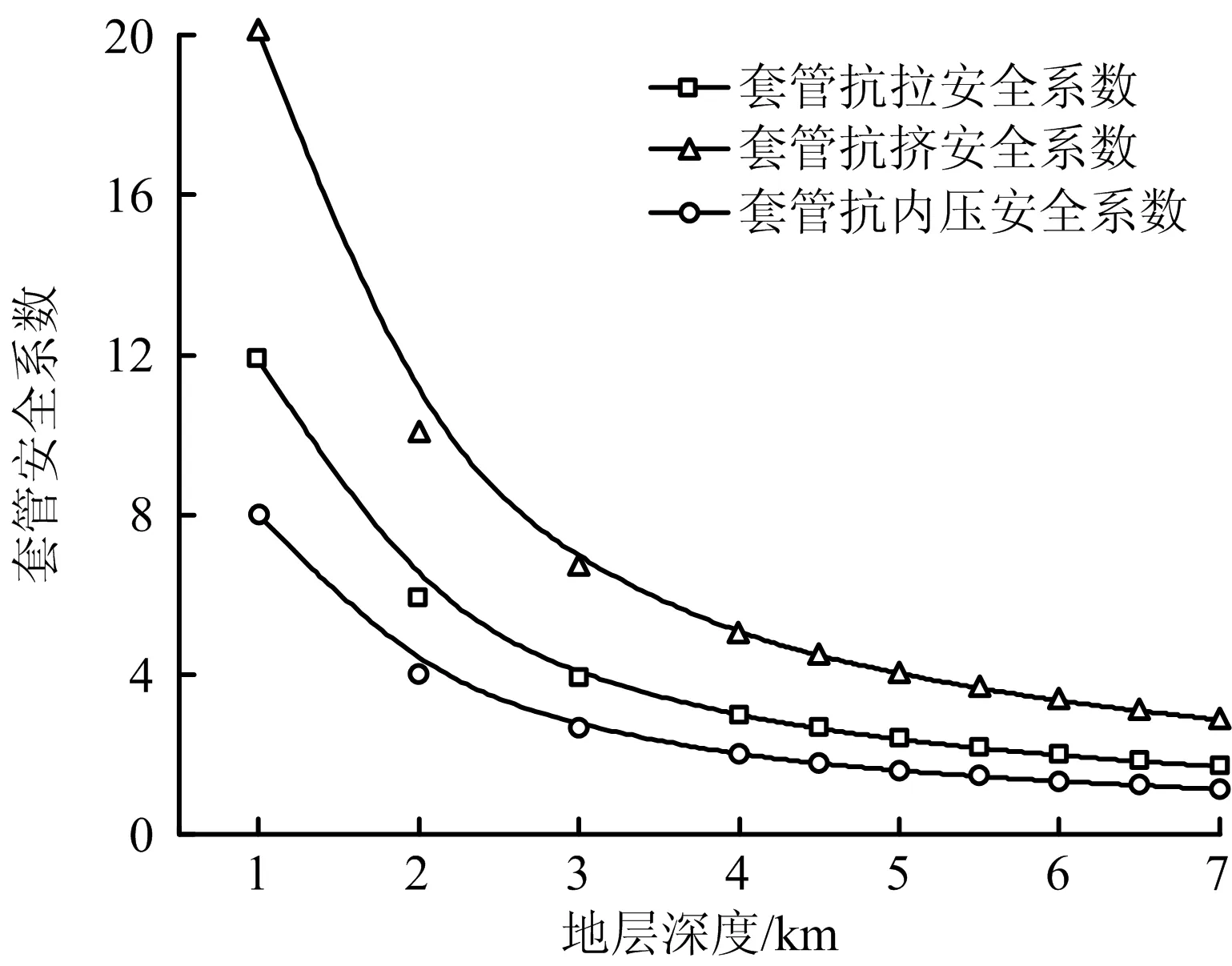
图1 强度安全系数随地层深度变化曲线Fig.1 Changing curves of strength safety factor with stratum depth

根据API[12]，得P110#套管的屈服极限是785 MPa，套管屈服安全系数为1.25。数值模拟计算得到套管随地层深度变化的屈服安全系数，见表3，并绘制曲线见图2，则满足套管强度安全系数的地层深度为6.2 km。取地层深度为6 km进行细化分析，确定此深度下影响管柱的变量及参数，得到了井深6 km处管柱的剩余强度及其分布，如图3所示。

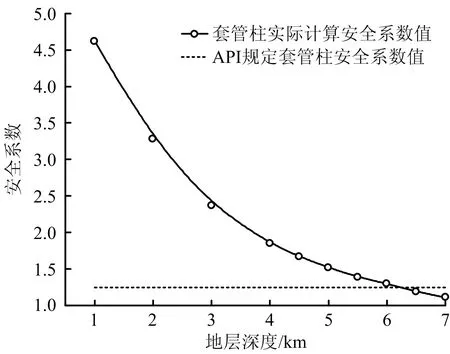
图2 抗屈服安全系数随地层深度变化曲线Fig.2 Changing curves of yield resistance safety factor with stratum depth

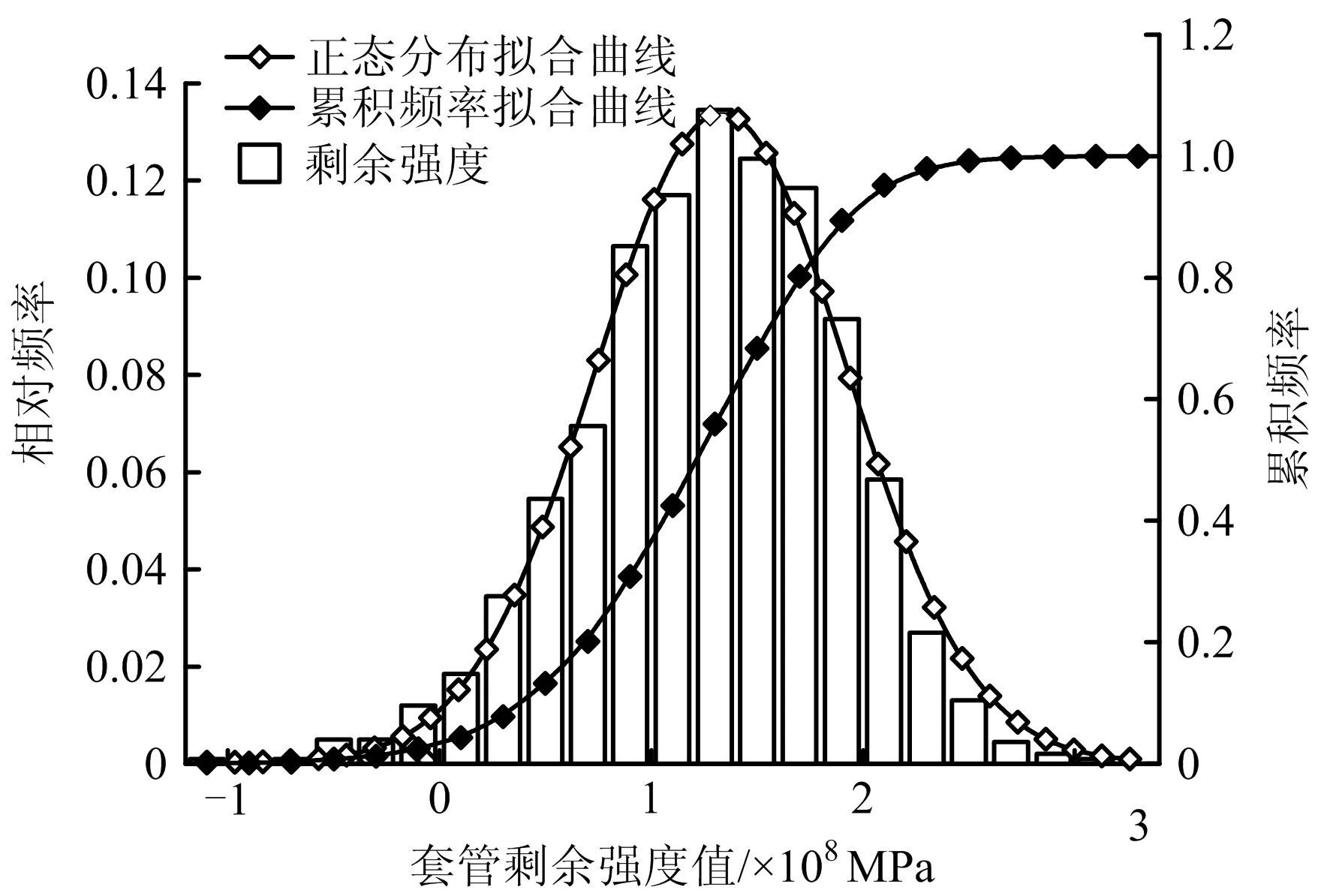
图3 管柱剩余强度正态分布及拟合曲线Fig.3 Normal distribution and fitting curve of residual strength of string

由图3可知管柱剩余强度符合正态分布，比较接近工程实际情况；进一步得到6 km处管柱剩余强度拟合方程和累积概率拟合方程，见式 (8)～(9)，曲线可靠度R2均在99%左右，说明曲线拟合效果较好，可为计算套管柱可靠性作参考。式(8)(9)所示：

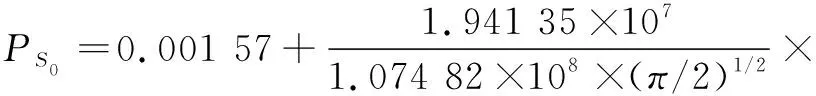
(8)

(9)

进一步计算得到置信度水平为90%～99%的管柱剩余强度置信区间和套管柱的安全系数取值范围，如表4所示。

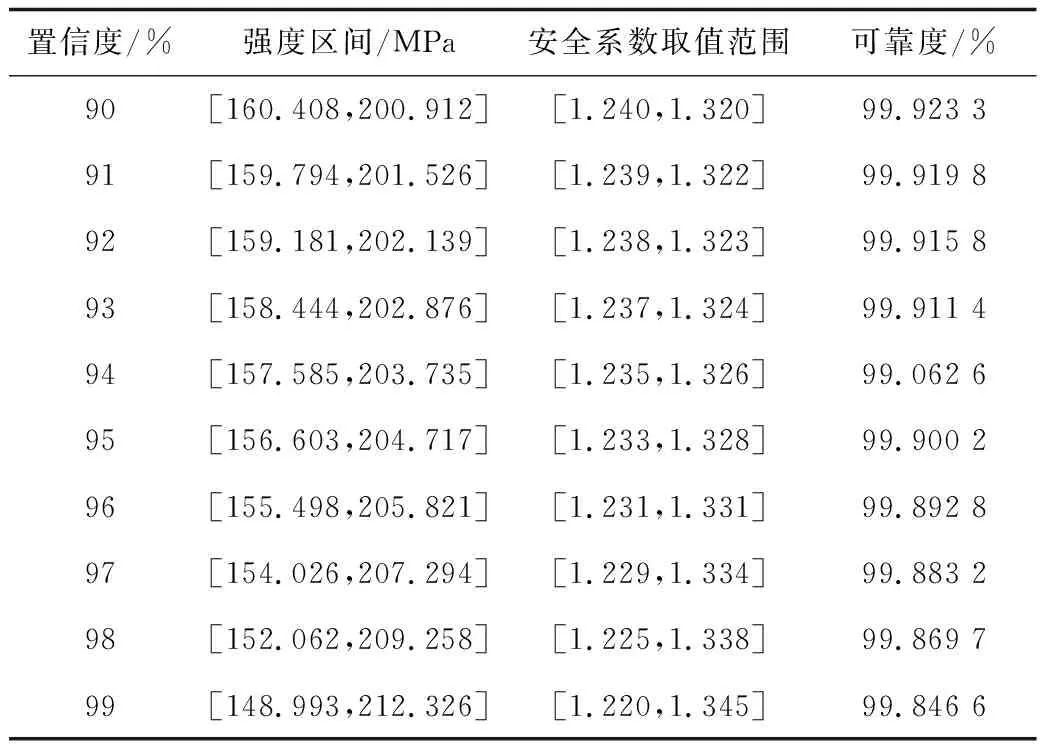
表4 不同置信度下套管柱剩余强度置信区间和安全系数取值范围Table 4 Confidence intervals for residual strength of string and valuing ranges of safety factors under different confidence levels

分析可知，置信度水平越高，套管柱的安全系数取值范围越大，但可靠性指标下降，即可靠度下降。且6 km深度处90%～99%置信度下套管柱的安全系数取值范围为1.220～1.345，参考API标准，取套管屈服安全设计系数为1.20，则6 km处套管柱可满足目标地区油气井管柱的安全设计要求。

4 结论

1)基于极限方程原理建立管柱可靠性模型，确定13个影响管柱可靠性的变量，主要包括管柱、水泥环和地层3方面的影响因素，对其进行统计分析，结果表明：模型中的变量均属于正态分布，并得到变量的相关分布参数。

2)计算得到油气井管柱剩余强度符合正态分布，进一步得到目标深度管柱剩余强度拟合方程和累积概率拟合方程，可为计算套管柱可靠性作参考。

3)采用蒙特卡洛方法对管柱可靠性进行模拟，得到管柱剩余强度的分布规律，计算出不同置信度水平下管柱的可靠度，分析得到管柱的安全系数取值范围为1.220～1.345，可满足管柱安全设计要求。