基于传递矩阵法的艉轴静态校中计算

赵子昂

（中国人民武装警察部队海警学院，浙江宁波 315000）

0 引言

船舶轴系将主机所产生的动力从柴油机动力输出端传递给螺旋桨，再由螺旋桨产生推力传递给整个船舶，使其正常航行。因此，船舶轴系是整个船舶动力装置最为重要组成部分之一[1]。

船舶轴系运转的可靠性，主要与其结构设计、材料、制造工艺和安装质量等因素有关，特别是安装质量的好坏，直接影响轴系能否在正常运转。安装质量差的轴系运转时很容易产生发热、轴承迅速磨损，甚至烧蚀、密封装置破坏和轴系振动等不良现象[2]，最终导致曲轴臂距差超过极限值等一系列影响主机正常运转的问题，进而破坏齿轮箱与其轴承的正常工作，并容易引起振动，直接影响船舶的安全航行[3]。因此，船舶轴系除有合理的结构设计和制造工艺外，还应具有良好的安装状态，使其全部轴承上的负荷及各轴段内的各项状态参数都处在合理范围内，以保证轴系可以长时间以良好的状态运转[4]。而安装状态的好坏主要取决于轴系校中质量，良好的校中质量，对保证船舶正常运转起到至关重要的作用[5]。特别是船舶尾轴部分，其与螺旋桨直接连接，运转工况受到多重因素影响，其产生的故障具有一定的隐蔽性，因此，有必要对其单独研究。

1 基本理论

本文利用基于Matlab计算软件的传递矩阵法，对船舶轴系模型进行静态条件下的各项参数计算，并加以分析。静态计算主要用于对轴系静止状态下的轴承受力计算及转角、挠度、弯矩和剪力这些相关参数的计算，并利用绘图软件绘画出相应图像，以便于对轴系状态进行进一步分析，得到更为合理的轴系布置方案，有利于轴系的合理校中安装。

当轴在平面上产生弯曲时，在工程力学上可以将其简化成梁结构，工程上梁结构的状态由用度y、转角θ、弯矩M和剪力T这4个主要参数来表征，而轴上某一截面的状态用一个矢量Z来表示，即：

式中：Z为某一截面的状态矢量；O为截面标号，O＝L（左）或O＝R（右）；i为对应截面的编号。

顾名思义，该计算方法的关键点在于利用矩阵进行了“传递”，而矩阵之间的“传递”表征的是每个单元的左右两端状态矢量之间的连结关系，其本质就是一个的线性方程组，利用线性代数中矩阵理论的知识可以对其中参数进行求解。对于一个中间没有任何隔断的连续梁实体，倘若仅知道其中某一点的状态矢量，便可通过矩阵间的传递关系对整个梁实体上的各点状态矢量进行求解计算。

在进行计算前，首先要对基本参数的正负值方向进行规定，图1中箭头所指方向为正反向。

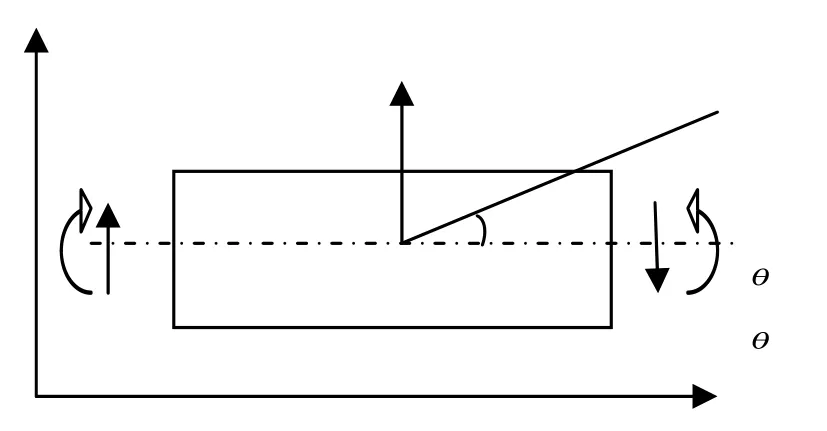
图1 系统的符号规定

2 艉轴试验台试验

2.1 试验台搭建

艉轴试验台从自由端到动力输出端依次由电机、变频调速器、连接法兰、艉轴、螺旋桨和各个轴承（中间轴承、艉轴承）组成，相应的辅助装备由试验平台、各种连接辅助部件及传感器等部件组成。图2为试验台全貌，表1为试验台设备主要性能参数。

图2 船舶艉轴实验台

表1 试验台设备性能参数

在连接法兰与中间轴承之间、中间轴承与艉前轴承之间、艉前轴承与艉后轴承之间分别安装好3个应变片，定义其为1#、2#、3# 3个测量截面，对艉轴进行盘车，利用传感器以测量其应力，再通过公式推导便可计算出其对应位置的弯矩值。

关于应变片的基本原理和安装相对复杂繁琐，本文受篇幅限制不过多赘述。

2.1 试验

本文利用应变片对上面所述的试验台的1#、2#、3# 3个截面的静态弯曲应变信号进行采集。

把中间轴承、艉前轴承、艉后轴承完全排布在一条直线，此时便是挠度为零的情况下，进行安装后的直线校中实测应变数据采集会得到一系列的数据，利用软件将数据进行绘制可得如图3～图5所示。

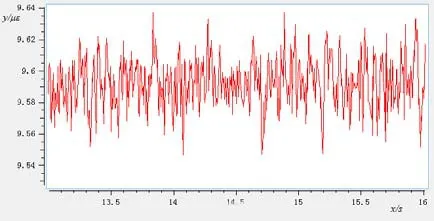
图3 1#测量截面处的弯曲应变信号

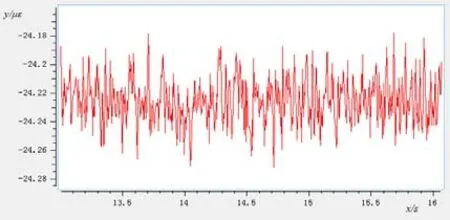
图4 2#测量截面处的弯曲应变信号

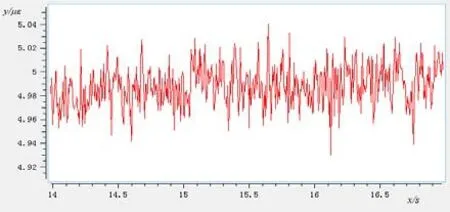
图5 3#测量截面处的弯曲应变信号

对上述信号取均值后，代入梁结构的弯举计算公式便可进行计算，得到对应3个测量节点的弯矩值。

3 计算结果

3.1 理论计算结果

把编辑好的程序导入Matlab软件中，输入执行程序命令，便可得到挠度、弯矩、转角、剪力及轴承负荷值的计算结果数据，再讲导出结果绘制成图像后生成图片格式导出。状态参数图像的横坐标为艉轴上对应位置，单位为m，坐标轴上0坐标点为螺旋桨自由端，从左向右分别为艉后、艉前和中间轴承所对应的位置，一直到坐标轴上4.07 m处，为电机转子的自由端，如图6所示。

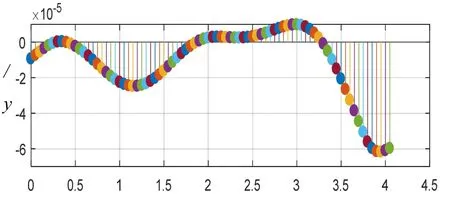
图6 直线校中挠度图

通过表2中的轴承负荷计算值可以发现，艉后轴承更靠近螺旋桨，直接导致导致承受负荷最大；受中间轴承靠近艉轴与中间轴的连接法兰处，到链接法兰重力影响，中间轴承负荷值也较大；艉前轴承负荷值负荷相比前两者较小，因此对该艉轴进行直线校中，各轴承荷分配并不十分均匀。

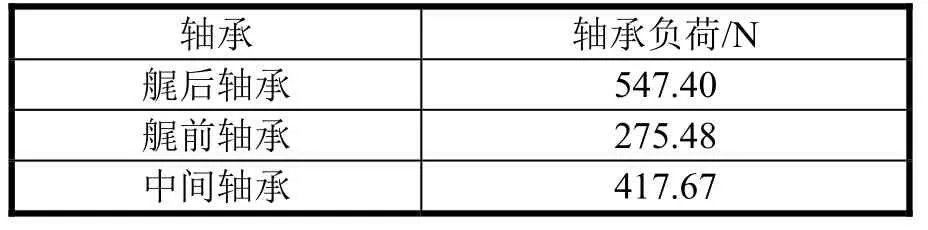
表2 轴承负荷计算值

由图6可知，中间轴承到连接法兰处的挠度逐渐降低，尤其是连接法兰处，由于连接法兰质量较大，导致其挠度值是整个艉轴的极值点。受到艉轴刚度影响，中间轴承前端挠度的降低，使得艉前轴承和中间轴承的轴段挠度为正值。艉前和艉后轴承距离较长，受到重力作用后轴段的挠度为负值。艉后轴承后端受到螺旋桨重力较大的影响，这一段挠度也成负值。

转角指的是梁横截面间的相对角位移。图7为转角图，表达的是艉轴转角值的变化趋势，能够反映轴系在铅垂面上弯曲的剧烈程度及弯曲的方向，转角值为正值且较大的是中间轴承后的一段及艉前轴承和艉后轴承前的2段（图7中横坐标1.5～1.6和0.5～0.9这2段）。

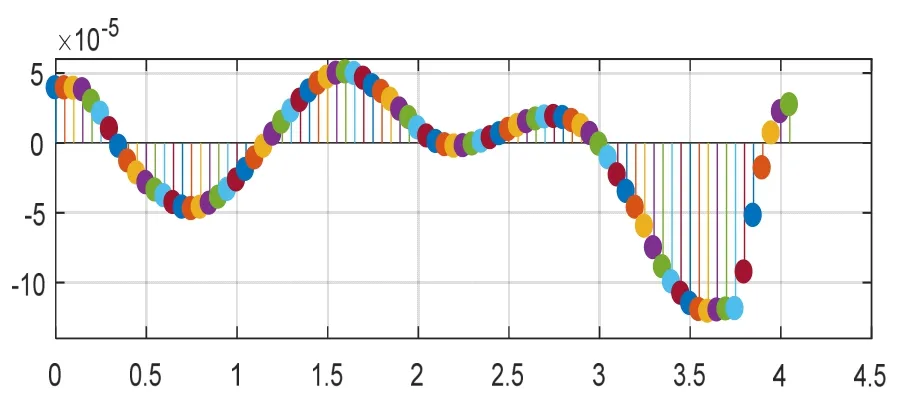
图7 直线校中转角图

观察图8可以发现，艉轴中各个轴承支点所在位置的弯矩值均较大，尤其是艉后轴承和中间轴承所在位置，均承受着较大的弯矩。由于轴的受重力影响，3个轴承中的各两轴承中间轴段也产生一定弯矩，电机内部两轴承之间部分也产生了较大的弯矩。

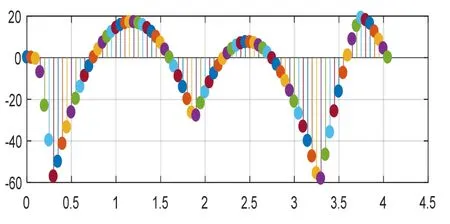
图8 直线校中弯矩图

图9为艉轴直线校中剪力图，反映了整个轴系各处节点的剪力分布状况。由图9可知，剪力围绕轴承支点左右正负交替，最大值处为艉后轴承支点上靠近螺旋桨一侧，这主要是艉后轴承部位受到螺旋桨较大重力的影响。

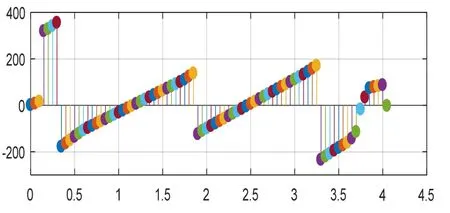
图9 直线校中剪力图

3.2 基于实测的计算结果

本试验台轴系的材料为碳钢，试验台艉轴的弹性模量值为206 GPa，代入公式后得到如下计算结果：M1＝17.742 1 N·m；M2＝-50.311 5 N·m；M3＝-12.866 0 N·m。

将上述3个截面弯矩测量结果带入事先编写好的基于实测值的传递矩阵法计算程序，利用事先编写好的程序带入Matlab进行计算得到3个不同的基于实测值的计算结果。受文章篇幅限制，本文仅以1#测量截面得到的结果带入基于实测计算的程序结果作为展示，结果如表3和图10～图13。

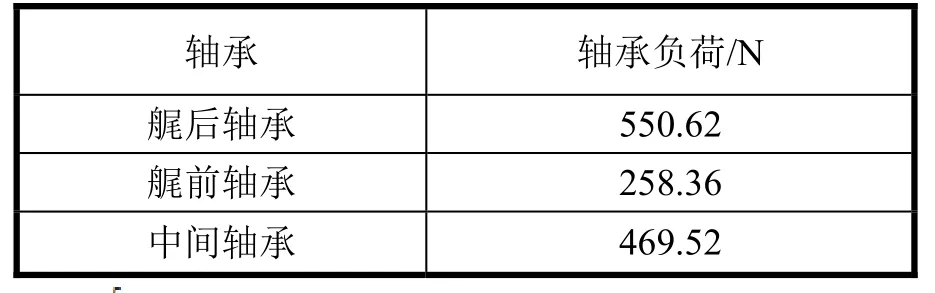
表3 1#测量截面轴承负荷值

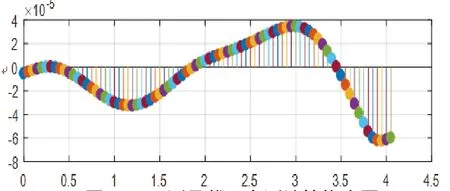
图10 1#测量截面实测计算挠度图

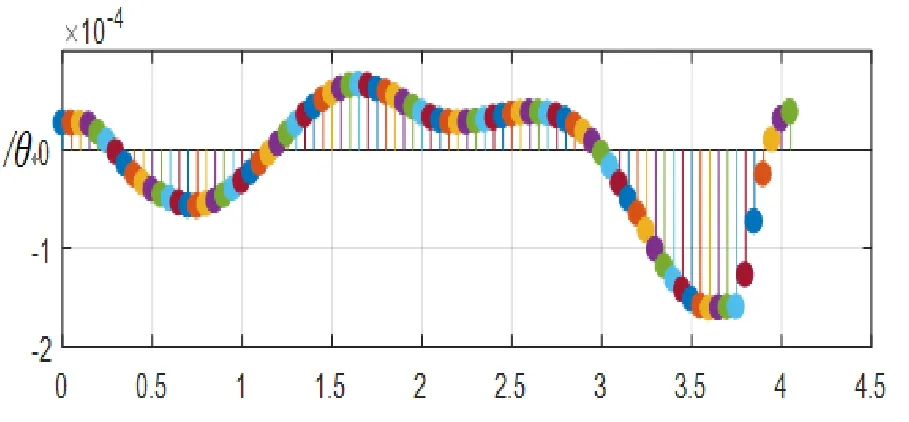
图11 1#测量截面实测计算转角图

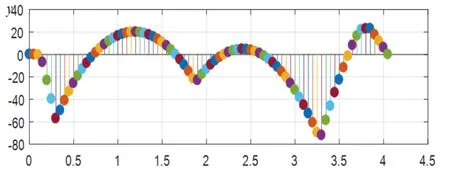
图12 1#测量截面实测计算弯矩图

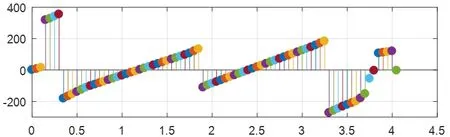
图13 1#测量截面实测计算剪力图

4 结论

将利用MATLAB软件对艉轴试验台进行传递矩阵法的直线校中的各项参数计算结果与基于1#测量点的实测值的计算结果进行对比发现，二者所得的轴承负荷以及其他各项数据及变化趋势基本相符。基于实测值的计算程序只能满足输入一个节点弯矩值并进行计算，下一步可将计算程序进一步优化，使其可以同时带入多个实测点的弯矩值，得到基于多个实测值的艉轴各项状态参数。利用基于实测值的传递矩阵法的校中计算，对轴系合理校中的安装布置提供更好的理论依据。