同侪激励机制下政府补贴对制造商绿色研发影响的演化博弈分析
卢 超 程海芳 蔡建湖
(1. 华中科技大学管理学院; 2. 杭州电子科技大学管理学院)
1 研究背景
推动绿色制造不仅需要技术研发、市场需求的内在驱动,同时也需要绿色政策、发展环境的外部驱动。绿色制造补贴是提升绿色技术创新力和绿色产能的激励政策。在《“十三五”节能减排综合工作方案》《中国制造2025》《工业绿色发展规划(2016~2020年)》等国家政策贯彻下,我国地方政府纷纷将绿色制造补贴纳入政策支持体系,对制造企业的绿色生产研发、节能减排起到了积极作用。例如,在新能源汽车补贴激励下,2015~2020年我国的新能源汽车产业累计推广新能源汽车超过450万辆,占全球50%以上。补贴政策推动了绿色制造发展,部分学者分别从行业发展[1]、外部机遇[2]、企业形象[3]、生存能力[4]等角度研究了政府补贴对绿色制造的正面作用。WANG等[1]研究发现,多种绿色补贴策略对回收再制造企业发展都起到不同程度的积极作用。WU[2]认为,绿色制造补贴会增加企业的外部融资机会,有利于企业研发创新。XIE等[3]通过内容分析方法,研究发现绿色制造补贴提升了绿色研发创新力和制造商的绿色形象。JIAO等[4]认为,绿色制造补贴通过绿色研发水平和产品竞争力间接提高制造企业的生存能力。

演化博弈理论结合了博弈分析和动态演化分析,被广泛应用于各类经济行为[13, 14]、政府规制[15, 16]研究,也适用于补贴机制的研究分析。针对长期导向的补贴政策问题,相关文献主要集中于研究奖励-惩罚结合的补贴激励机制。LONG等[17]建立绿色建筑生产商与回收商的演化博弈模型,研究基于奖惩机制的政府绿色补贴和绿色发展绩效对双方行为策略的影响。LIU等[18]以电动汽车产业为背景,研究不同补贴-税收策略下制造商行为策略的演化路径。尽管带有惩罚的激励机制能够形成长期的政企合作关系,但部分研究认为惩罚不具有经济效应[19],可能带来社会报复行为[20],纯奖励的激励机制比带有惩罚的激励机制创造更多的社会收益[21]。然而,鲜有文献研究无惩罚的政府补贴机制。综上,本研究拟基于“多资金渠道的无惩罚性绿色补贴机制”这一构念,设计同侪激励下的地方政府补贴机制,基于演化博弈理论研究地方政府补贴行为和制造商研发行为的交互影响。
2 问题描述与假设
同侪激励机制描述为:由全体制造商出资组建同侪激励基金池,政府通过绿色补贴将官方补贴与基金一起发放给环保达标的制造商。具体而言,为了激励制造商研发高绿色度的产品,政府提出一种制度性的激励方案——制造商需要向同侪激励基金池中投入一笔固定数额的承诺资金,以获得政府许可的绿色生产资质,并履行积极研发和致力环保的承诺。政府接管基金池,根据制造商的实际研发状况,将基金和官方补贴统筹支付给履约的制造商。
同侪激励机制是基于现实依据与理论依据设计的。现实依据方面,该机制最早产生于联合国在2016年颁布的《巴黎协定》。缔约国家达成共识,大部分发达国家是温室气体排放大国,需要在治理气候问题上承担更多的责任,因此,缔约的发达国家需向发展中国家提供重要资金,用于激励后者的节能减排项目。理论依据方面,YANG等[22]基于公共品博弈论证了组织内部激励的理论可行性。
常规的政府补贴资金完全来源于官方,政府的财政压力可能导致补贴资金拖欠或停发等严重问题,补贴政策可能面临失效。与此不同,同侪激励机制下的补贴支出资金由官方补贴和同侪激励基金两部分组成,地方政府既是官方补贴资金的支付方,也是基金的管理方。由此可见,多资金渠道能够缓解财政压力并保障补贴政策的长期导向,有利于提高地方政府的财政支付意愿;同时,政府提供的官方补贴并未脱离政府补贴的无偿性原则,制造商支付的基金也以环保导向进行二次分配。鉴于此,本研究将着重探讨同侪激励下的补贴政策合理性,并阐明政企双方在同侪激励机制影响下的长期合作机理。
在环保效益、补贴预算、同侪激励等因素影响下,地方政府会改变补贴行为动机,存在政策收益时政府会持续实施补贴政策,反之则放弃补贴;在产品利润、补贴支出等因素的影响下,制造商绿色研发的积极性也不同。政企双方的行为策略选择符合演化博弈的研究范式,因此,基于演化博弈理论对政企双方行为进行深入分析,提出以下问题:哪些情境或者演化规律中的政企合作关系是长期稳定的?是否存在固定的合作策略?若不存在固定策略,则政策应该如何完善?
针对以上研究问题,对模型作如下假设:
假设1博弈双方均符合有限理性人假设。在某一时刻,政府选择补贴的概率为x(t),制造商选择积极研发的概率为y(t),满足约束条件:0≤x(t)≤1,0≤y(t)≤1。
假设2为了简化问题,假设种群内不存在个体差异和地域差异,每个制造商都承担相等的环境保护责任,投入相等的同侪激励基金。
假设3地方政府存在财政压力,官方补贴资金限于维持环保政绩,即补贴支出由环保政绩和同侪激励基金两部分组成。
3 模型建立与稳定性分析
3.1 基本模型
模型中的博弈双方为地方政府群体与制造商群体,两者均为有限理性的主体。根据演化博弈理论,博弈主体均采用两种策略。制造商群体采用积极研发(P)和消极研发(N)两种策略,其可行策略集合为{P,N};地方政府可能面临财政预算紧张,有同侪激励补贴(I)和放弃补贴(U)两种策略,其可行策略集合为{I,U}。
制造商在积极研发和消极研发策略下对应的总利润分别为ΠP、ΠN,产品绿色度分别为eP、eN,政府补贴的启用基准为eB(eP>eB>eN),政府因制造商绿色研发而产生的环保政绩分别为gseP、gseN,其中gs为单位绿色度的环境效益。政府只对产品绿色度高于补贴启用基准的企业予以补贴,即补贴积极研发的制造商,则地方政府的补贴支出为M=k(v+gseP),其中k为基于同侪激励基金v和环保政绩的补贴系数。由于同侪激励是无惩罚的激励机制,地方政府对消极研发的企业不补贴也不惩罚;但是,政府实施补贴策略后,全体制造商都要交付同侪激励基金v。综上,政企双方博弈的支付矩阵见表1。

表1 地方政府与制造商之间博弈的支付矩阵

(1)
根据演化博弈理论,构建出政府的复制动态方程,由式(1)可得
F(x)=dx/dt=x(1-x)((1-ky)v-kyePgs)。
(2)
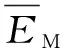
(3)
同理可得,制造商的复制动态方程为
F(y)=dy/dt=y(1-y)(kvx+kxePgs-Πn+ΠP)。
(4)
所以,由政府与制造商组成的二维复制动态方程组为
(5)
3.2 基本模型的稳定性分析
令式(5)中F(x)=0,F(y)=0,可以求得(0,0)、(0,1)、(1,0)、(1,1)、(x1,y1)是复制动态方程组的均衡点。其中,x1=(Πn-ΠP)/(k(v+ePgs)),y1=v/(k(v+ePgs))。
利用Jacobian矩阵判断均衡点是否存在演化稳定策略(ESS)。由式(5)得Jacobian矩阵为

(6)
根据Jacobian矩阵的稳定性分析方法,对均衡点进行稳定性分析的结果见表2。

表2 均衡点的稳定性分析
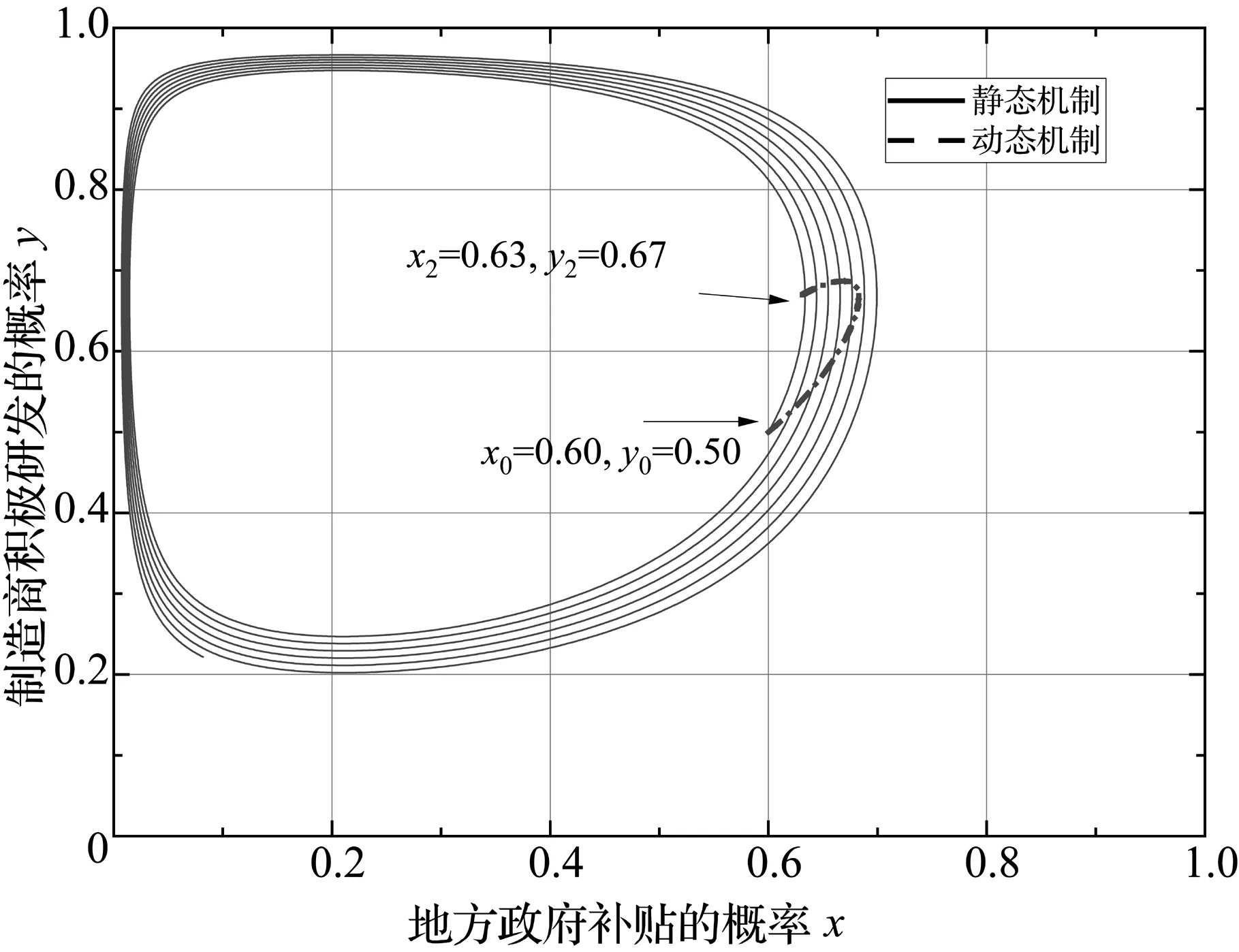
不同情境下的地方政府和制造商演化博弈相位图见图1。对于每个情境的成立条件和管理意义,具体分析如下:①情境Ⅰ的成立条件是制造商积极研发的利润高于消极研发,且政府补贴支出大于同侪激励基金。当满足条件ΠP>ΠN和M>v,制造商选择积极研发,地方政府选择放弃补贴,对应的演化博弈轨迹见图1a。此时,均衡点(0,1)为ESS。②情境Ⅱ的成立条件是制造商积极研发的利润高于消极研发,且政府补贴支出小于同侪激励基金。当满足条件ΠP>ΠN和M 以上分析表明,在政企双方的演化博弈中,①当制造商采用积极研发的策略所得利润高于消极研发时,制造商始终选择积极研发,而地方政府是否实行补贴策略取决于同侪激励基金和补贴支出的大小关系;②当制造商消极研发的策略所得利润高于积极研发时,若ESS存在,则政府始终选择同侪激励补贴的策略,而制造商的研发策略选择取决于政府补贴支出和制造商采用两种策略的利润差额的大小关系;③当制造商消极研发的策略所得利润高于积极研发时,若ESS不存在,则政企双方策略选择的演化轨迹是围绕中心点动态循环的闭轨环线,演化系统不存在固定的合作策略。具体来说,地方政府的补贴政策激励了更多的制造商采用积极研发策略,然而随着积极研发的制造商群体规模扩大,地方政府又因补贴支出过大而逐渐放弃补贴,此时积极研发的制造商群体规模又逐渐缩小。这种动态循环过程形成了“补贴困局”,增大了制造商和地方政府长期合作的难度,因此需要进一步完善补贴机制,以缓解基本模型中存在的系统不稳定性。 完善补贴机制的常规做法是引入被动惩罚,即当制造商消极研发的群体规模增大时,政府加大惩罚力度;反之则降低惩罚力度。此类做法已被大量文献[23, 24]采用,可以缓解系统不稳定。本研究所述的同侪激励无被动惩罚,需要对假设2进行调整,假设制造商投入的同侪激励基金数额不同。由于补贴支出M=k(v+gseP)中可供动态调整的变量为补贴系数k或同侪激励基金v,则可考虑将v作为动态参数,即v′(y)=(1-y)v。动态参数v′的解释为:当制造商积极研发的概率越高时,其支付的同侪激励基金越小;当制造商消极研发的概率越高时,其支付的同侪激励基金越大。将动态调整后的同侪激励补贴机制简称为“动态机制”,以对应于前述的“静态机制”。同理,由政府与制造商组成的二维复制动态方程组为 (7) 令式(7)中F(x)=0,F(y)=0,可以求得(0,0)、(0,1)、(1,0)、(1,1)、(x2,y2)是复制动态方程组的均衡点。其中,x2=(Πn-ΠP)/(k(v′+ePgs)),y2=v′/(k(v′+ePgs))。 在动态同侪机制作用下,政企双方行为策略的演化轨迹由围绕中心点循环的闭轨环线转变为趋向(x2,y2)的螺旋环(见图1g)。情境Ⅵ的成立条件是制造商消极研发的利润高于积极研发,政府补贴支出大于制造商采用两种策略的利润差额,且政府补贴支出大于动态调整后的同侪激励基金。满足情境Ⅵ的成立条件时,制造商和地方政府的策略选择会随对方策略改变而不断调整,最终趋向渐近稳定。 综上,静态机制和动态机制下的激励模型具有如下特点:①动态补贴机制是对静态补贴机制的政策完善,两者均无被动惩罚性,制造商交付基金等同于获取生产资质;②地方政府有财政压力时,例如情境Ⅴ,同侪激励机制依然能够确保政府和制造商之间长期稳定的合作关系;③情境Ⅰ~情境Ⅴ中,制造商投入的基金数额相等,避免了基金份额不均而导致的群体内部矛盾。 考虑到制造商的利润与市场因素、产品质量有关,如消费者需求、产品绿色度、产品价格等,在数值模拟中参考了DAI等[25]、温兴琦等[26]的研究。将制造商的利润函数定义为Π=Q(p-c)-R,其中消费者需求定义为Q=α-βp+γe,研发投入成本定义为R=ηe2,产品成本定义为c=c0+cee,其中,α代表基础市场;β代表消费者的价格偏好水平;γ代表消费者的绿色偏好水平;ce代表单位绿色度的成本。各个参数设置为β=0.20,ce=0.35,p=4,eP=0.30,eN=0.05,eB=0.15,γ视不同情境而定,其余参数为1。制造商和政府行为策略的初始概率为x0=0.6,y0=0.5。下面分析不同情境下同侪激励基金、补贴系数对政企双方行为策略的影响。 图2 参数调整对双方行为策略的影响(情境Ⅰ、Ⅱ) 情境Ⅰ、Ⅱ下参数v、k调整对双方行为策略的影响见图2。当γ=0.8时,v、k取得对应值后满足情境Ⅰ、Ⅱ的成立条件。双方的行为策略随着侪激励基金v和补贴系数k的变化而调整,且参数均以等比例调整。例如,实线组(情境Ⅰ)表示k取值0.38,v分别取值0.07、0.10、0.15,以及v取值0.07,k分别取值0.25、0.38、0.56的模拟结果。情境Ⅰ中,随着同侪激励基金、补贴系数分别增大,双方行为策略的演化时间均相应缩短,同侪激励基金相较于补贴系数的调整效果更显著。在补贴系数较小或者同侪激励基金较高的情况下,地方政府的补贴概率一开始处于增长状态,随着时间推移,制造商群体的研发积极性增强,政府转向放弃补贴,直到达到稳定状态。当v=k={0.07,0.10,0.15}时,双方行为策略的调整过程与情境Ⅱ吻合,积极研发的制造商群体规模始终增大,地方政府保持财政收支平衡,因此双方一直处于合作状态直到形成稳定均衡。 情境Ⅲ下参数v、k调整对双方行为策略的影响见图3。当γ=0.05时,v、k取得对应值后满足情境Ⅲ的成立条件。为了更清楚地表明情境Ⅲ中M和v相对大小关系产生的差异,令当前情境下初始概率x0=0.6,y0=0.7。v={0.010,0.015,0.023},k={0.070,0.100,0.150}表示政府补贴支出大于同侪激励基金(M>v)的情况,v={0.010,0.015,0.023},k={0.027,0.040,0.060}表示政府补贴支出小于同侪激励基金(M 动态机制对双方行为策略的影响见图4。此时γ=0.05,v=0.50,k=2,满足当前情境的成立条件。在静态机制下,制造商积极研发的概率在[0.21,0.96]区间内震荡波动,政府补贴的概率在[0.01,0.70]区间内震荡波动,随时间向边界扩散并形成闭轨环线;在动态机制下,制造商积极研发的概率会随时间收敛于0.67,政府补贴的概率会随时间逐渐收敛于0.63,最终形成趋向于渐近稳定焦点(0.63,0.67)的螺旋线。随着同侪激励基金的增加,政企双方合作的概率也会增大。由于补贴支出过高和制造商研发积极性降低两方面原因,在静态机制下双方的策略选择无法达到稳定状态,只有当地方政府对同侪基金的调控处于动态时,才能稳定调动制造商研发积极性。 情境Ⅴ下制造商与政府的行为策略随参数调整的演化轨迹见图5。当γ=0.05,v={0.07,0.10,0.15},k={0.12,0.18,0.27}时满足情境Ⅴ的成立条件。当前情境下,地方政府处于财政收支平衡状态,政府实施补贴策略调动了制造商的研发积极性,双方的行为策略朝着相互合作的方向发展。相较于调整补贴系数,调整同侪激励基金有更强的合作促进效果。 图5 双方行为策略的演化轨迹(情境Ⅴ) 上述实验表明:①制造商的利润、地方政府的补贴支出分别决定其对应的纯策略选择,两者各自倾向于追求更高的利润和更低的补贴支出,补贴资金不足会造成地方政府放弃补贴和制造商不响应补贴政策两种行为;②相较于补贴系数,调整同侪激励基金可以更有效地平衡财政收支,促进政企双方合作;③补贴支出较高会使双方的合作关系不稳定,动态调节同侪激励基金能够调动制造商研发的积极性,使双方的行为策略更快形成稳定均衡。 不稳定的演化系统中,参数对双方行为策略的影响是不确定的。为了更准确地分析系统参数对双方行为策略的影响,采用蒙特卡洛模拟方法,在对应参数调整区间内随机均匀选取200个取值进行敏感性分析,研究系统不稳定时关键参数的敏感性。图例中的50%、75%、95%、100%分别表示了均匀选取0~50%、50%~75%、75%~95%、95%~100%的随机参数值,并显示出相应区域的模拟结果。 在区间[0.1,1]调整同侪激励基金的敏感性分析结果见图6。由图6可见,除了图6c,系统对同侪激励基金变化都表现出较高的敏感性。一方面说明同侪激励基金是高敏感性参数,对其调节具有更强的针对性;另一方面说明动态调控会间接抑制参数自身的敏感性,使地方政府的政策执行更为灵活简便。 在区间[0.1,6.0]调整补贴系数的敏感性分析结果见图7。对比图6和图7可见,系统对补贴系数k表现出低敏感性,对研发投入水平η、价格偏好水平β、绿色偏好水平γ等环境参数的敏感性分析也得出类似结论。由此可见,同侪激励是影响政策实施效果的重要因素,地方政府在实施补贴过程中既要把握补贴力度,关注到市场环境、企业研发状况带来的变化,更应该合理调控同侪激励基金。 综上,在地方政府对制造商实施同侪激励下的补贴政策时,调整同侪激励基金对政策实施效果的影响最为显著。在不稳定的政企合作关系中,政策调控的难度加大,动态机制的灵活性减轻了地方政府的政策调控压力,进一步增强了补贴政策的长期性和可预期性。 本研究在倡导绿色研发制造的背景下,基于有限理性的基本假设构建了地方政府与绿色制造商的演化博弈模型,考虑到地方财政压力的问题,设计了包含同侪激励基金和官方补贴两种资金渠道的补贴机制,从理论上归纳了静态、动态同侪激励机制下的政企双方交互行为的不同情境和成立条件,并通过数值模拟研究了不同参数对演化系统的敏感性影响。研究表明:①政企行为策略的变化受到生产利润、补贴支出、同侪激励基金三者共同影响而形成不同的演化稳定策略, 较低的政府补贴支出仍能长期激励制造商绿色研发;②调整同侪激励基金或补贴系数可以平衡财政支出,使双方行为向着长期合作的方向演化;③政府的补贴支出应当适度,支出过度会导致“补贴困局”,动态同侪激励机制能够完善补贴政策,消除演化系统的不稳定性;④相较于补贴系数,同侪激励基金具有更高的参数敏感性,动态调整同侪激励基金的效果更为显著。 本研究以政府基于研发投入成本的单性补贴为例,未来可以比较产量挂钩补贴与脱钩补贴、同侪激励与奖惩激励等不同补贴策略的优劣性。此外,同侪激励机制对于防止骗补寻租现象的有效性,以及同侪激励基金保值增值等经济效益问题,是下一步的研究方向。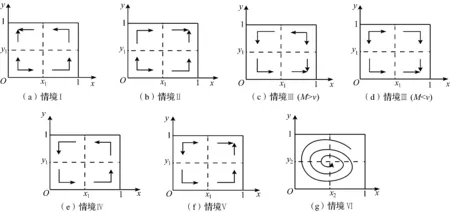
3.3 动态同侪激励下的博弈模型
4 数值模拟
4.1 不同情境下参数对政企双方行为策略的影响



4.2 参数敏感性分析

5 结语