异地多站联合守时方法研究

赵书红，董绍武,3，袁海波,3，白杉杉，屈俐俐，李孝辉,3

异地多站联合守时方法研究

赵书红1,2，董绍武1,2,3，袁海波1,2,3，白杉杉1,2，屈俐俐1,2，李孝辉1,2,3

（1. 中国科学院 国家授时中心，西安 710600；2. 中国科学院 精密导航定位与定时技术重点实验室，西安 710600；3. 中国科学院大学，北京 100049）

异地多站联合守时方法，一方面可以整合有限的原子钟资源，提高各实验室原子钟的利用率，以及综合时间尺度的稳定性和准确性；另一方面提供了一个稳定和可靠的驾驭参考，提升各站点的实时输出物理信号性能。本文基于中国科学院国家授时中心的多场区和多个远程比对链路的优势，分别在蒲城、临潼和西安场区开展实时物理信号产生试验，综合这些场区的原子钟数据，计算产生联合时间尺度TA。以该时间尺度TA为参考，分别对西安和临潼场区的主钟进行驾驭，最终西安和临潼两站产生的实时物理信号与协调世界时UTC的相位偏差保持在±3 ns。试验表明，采用异地多站联合守时方法，可以实现异地多站复现的物理信号一致性。

联合时间尺度；频率驾驭；ALGOS 算法；最优二次型高斯控制算法

0 引言

高精度时间频率已经成为一个国家科技、经济、军事和社会生活中至关重要的参量，关系着国家和社会的安全稳定。随着时间频率的发展和性能提高，推动了基础科学研究（相对论、引力场理论等），以及诸多科学实验和工程技术领域（长基线干涉、载人航天和海洋监测、深空探测）等的飞速发展。

目前“最准确”的时间是国际标准时间——协调世界时（UTC，Coordinate Universal Time），UTC是由国际权度局（BIPM）发布，是国际原子时TAI（International Atomic Time）和世界时UT1（Universal Time）的综合。BIPM通过整合全球89个时间实验室的400多台原子钟数据（截止2019年12月），以及十多台基准钟数据计算得到既稳定又准确的国际原子时，再根据国际地球自转服务组织提供的世界时测量数据，对上述国际原子时进行闰秒调整，形成了国际标准时间UTC。但UTC是“纸面时间”，且滞后40～45 d，不能够满足用户对高精度时间信号的实时性要求，因此各守时实验室需要独立产生和保持一个稳定的标准时间UTC()，即UTC在各守时实验室中的物理实现，为不同守时实验室的缩写。一个国家或地区的标准时间UTC()，一旦建立将持续运行，从而成为国家或地区中经济和社会生活不可或缺的时间标准[1-2]。

通常，多数守时实验室利用部署在本地的若干台自由运行的原子钟数据，通过适当的数学方法进行综合计算，形成一个综合的“纸面时”，称为“独立地方原子时”，用TA()表示。纸面时是基于原子钟的组合加权平均，它的性能一般比守时系统中任何一台原子钟更加稳定、准确可靠。以TA()作为本地实时物理信号的驾驭参考，对主钟频率源进行驾驭，从而得到标准时间UTC()，使其尽可能接近或符合纸面时的频率，因此纸面时的性能好坏是提供准确稳定的实时物理信号的关键。

一般情况下，守时钟性能越好，钟组规模越大，其保持的纸面时性能就越好。而有些时间实验室，仅仅运行有一台或者少数几台守时原子钟，难以形成准确、独立的纸面时。如果通过异地多站联合的手段形成综合时间尺度，一方面可以整合有限的原子钟资源，提高参与综合时间尺度计算的各实验室原子钟的利用率，提升综合时间尺度的稳定性和准确性。另一方面部分时间实验室不具有独立地方原子时或者不具备国际标准溯源能力，可以获得更稳定和可靠的驾驭参考源，有效提高时间实验室产生和保持的标准时间的综合性能。

2018年，我国正式筹备建设“高精度地基授时系统”，通过增补完善增强型罗兰授时系统，以及覆盖主要城市和用户的光纤时频传递网，将国家标准时间UTC（NTSC）以更高精度、更大范围传递给用户。高精度地基授时系统的建设地点分布较广，这些站点配置有性能优良的时频设备，可通过异地多站联合技术，将异地多站的时频设备联合起来，提高国家标准时间的性能，保障国家用时安全。本文综合中国科学院国家授时中心临潼场区、蒲城场区以及西安场区的原子钟数据，以及不同场区之间的远程时间链路比对数据，采用集中式计算的模式，搭建综合原子时比对网络，将蒲城场区和西安场区的原子钟数据和链路比对数据传递至临潼，在临潼处理中心统一处理并归算出综合时间尺度，并以该综合时间尺度为驾驭参考，在临潼场区和西安场区分别产生实时物理信号，分析不同场区复现的物理信号性能。

1 基本原理

1.1 ALGOS算法

每一台原子钟都可以产生一个时间尺度。由于每台钟都存在噪声和偏差，且每一种物理装备都有可能出现物理故障，为保持时间尺度的准确度和稳定度，采用原子时算法，使得生成的时间尺度稳定性优于钟组内单台钟的性能。

ALGOS算法是BIPM采用的原子时算法，也是当前国际上被多个守时实验室采用的本地原子时计算方法。ALGOS算法基本原理描述如下：

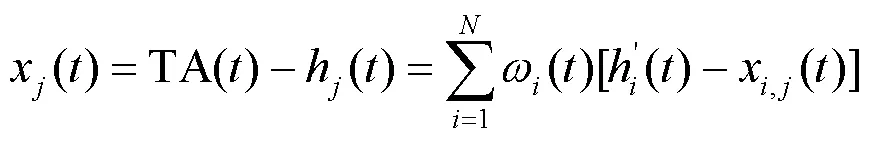
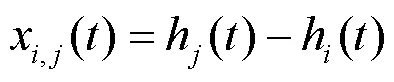
原子钟的频率预报模型为

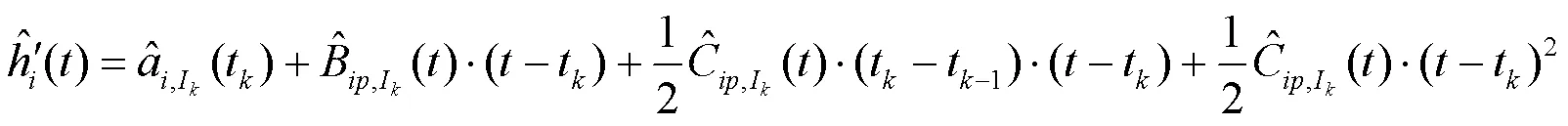
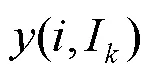
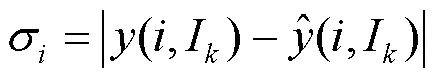
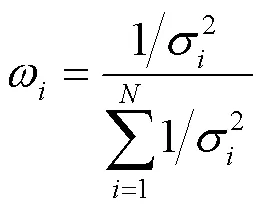
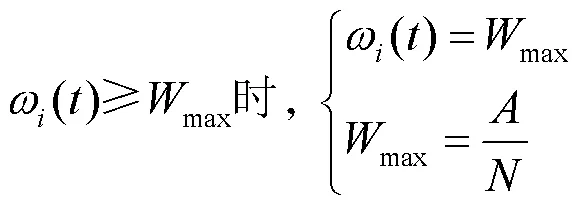
1.2 Vondrak平滑

异地多站联合守时，需要将多个实验室或站点的原子钟数据传送到数据处理中心，但在数据传递过程中，会将链路的噪声带入原子钟比对数据中，同时也必须考虑原子钟的自身噪声等。对原子钟数据和链路噪声的抑制，采用Vondrak平滑技术，其基本思想是建立的目标函数既要尽可能接近测量值，又要尽可能平滑[6-7]。

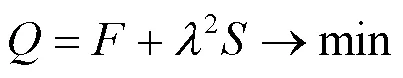
式（7）中

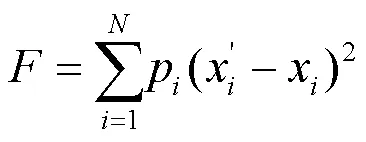
1.3 频率驾驭算法

频率驾驭算法采用Kalman算法与最优二次型高斯控制算法（LQG算法）综合，通过实时调整参数，计算出最优的频率驾驭量。频率驾驭算法采用LQG算法，利用最小化二次代价函数不断地逼近最优控制，再通过Kalman滤波方法，构造增益矩阵的递推公式，将控制值和滤波器不断迭代直至收敛，最终得到最优滤波器的目的。

1.3.1 Kalman算法

含有控制量的Kalman算法状态方程描述为

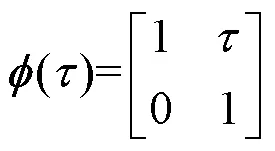
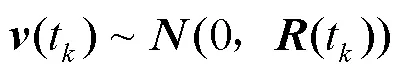
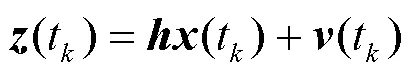
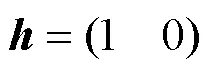
噪声协方差阵和测量方差阵的求解：

1.3.2 LQG算法

最优二次型高斯控制算法（LQG算法）是一种较为灵活的驾驭算法，通过调整和参数值，优化频率驾驭值。为保证LQG算法计算获得最优的主钟频率驾驭值，必须保证代价函数最小化[8-9]：

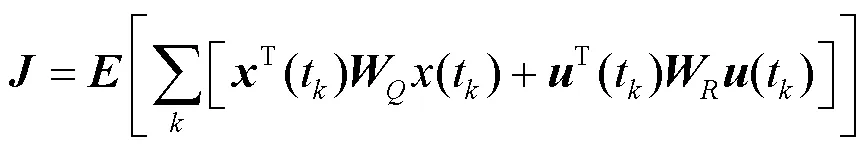
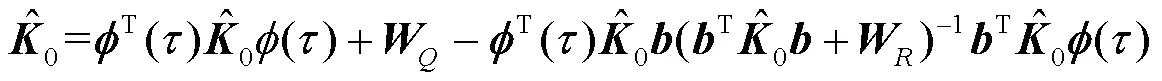
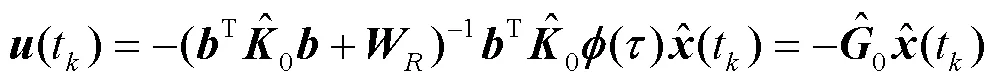
2 异地多站联合守时

异地多站联合守时采用集中式方式构建，利用本地原子钟比对系统，获取各站实验室内原子钟组的比对数据。采用GNSS CV/PPP、双向、光纤等远程比对手段，实现不同实验室间系统时间的溯源比对，最终获得异地多站的原子钟比对数据。参考国际标准时间产生（TAI/UTC）的模式，搭建综合原子时比对网络，选择一个实验室作为主站，其他实验室将原子钟数据和链路数据传递至主站，在主站统一处理并归算出综合时间尺度，以该综合时间尺度为驾驭参考，结合国际溯源比对结果，最终实现高精度异地多站联合时间的产生。在这种计算模式下，无论选择哪个实验室作为主站，采用相同的时间尺度算法和频率驾驭算法，最终产生的标准时间性能差异主要由主钟性能、参数设置不同等引起。异地多站联合守时包含原子钟数据预处理，综合原子时尺度计算和实际物理信号产生三个环节，计算过程如图1所示。

2.1 原子钟数据预处理

基于本地测量系统获得的原子钟数据，存在数据缺失、异常和噪声等情况，如果这些因素的影响没有被减弱或消除，最终会影响输出信号UTC()的控制精度。

国际上通用的高精度远距离时间传递技术包括卫星双向时间频率传递（TWSTFT）、GNSS CV/PPP、光纤等。通过综合原子时比对网络，将多个实验室或站点的原子钟数据传递到数据处理中心，但在数据传递过程中，受时间比对链路性能的影响，会将链路噪声带入原子钟比对数据中，同时远距离比对易出现异地原子钟数据的缺失、异常等情况。因此在参与综合原子时计算前，需要对原子钟进行数据预处理。

依据上述分析，在对原子钟数据降噪时，一方面要考虑传递链路引入的误差，另一方面还需要考虑内部比对系统引入的误差，以及原子钟自身噪声等[10-12]。

数据降噪采用Vondrak平滑算法，该算法的平滑因子选取是一个难点问题，只有当平滑因子的选取与噪声水平相符时，可以更加有效消除噪声。交叉证认法可以通过对数据序列中的一些样本的相互交叉证认来客观选取合适的平滑因子，有效解决了不同类型数据的平滑因子选取困难问题[13]。

原子钟数据预处理的过程包括完整性检测、粗差剔除、数据降噪等环节，其中涉及数据内插和外推算法、数据降噪方法等。只有消除这些异常因素的影响，才能获得有意义的分析结果。数据预处理结束，处理好的数据开始参与综合时间尺度计算。数据预处理模块的流程图如图2所示。

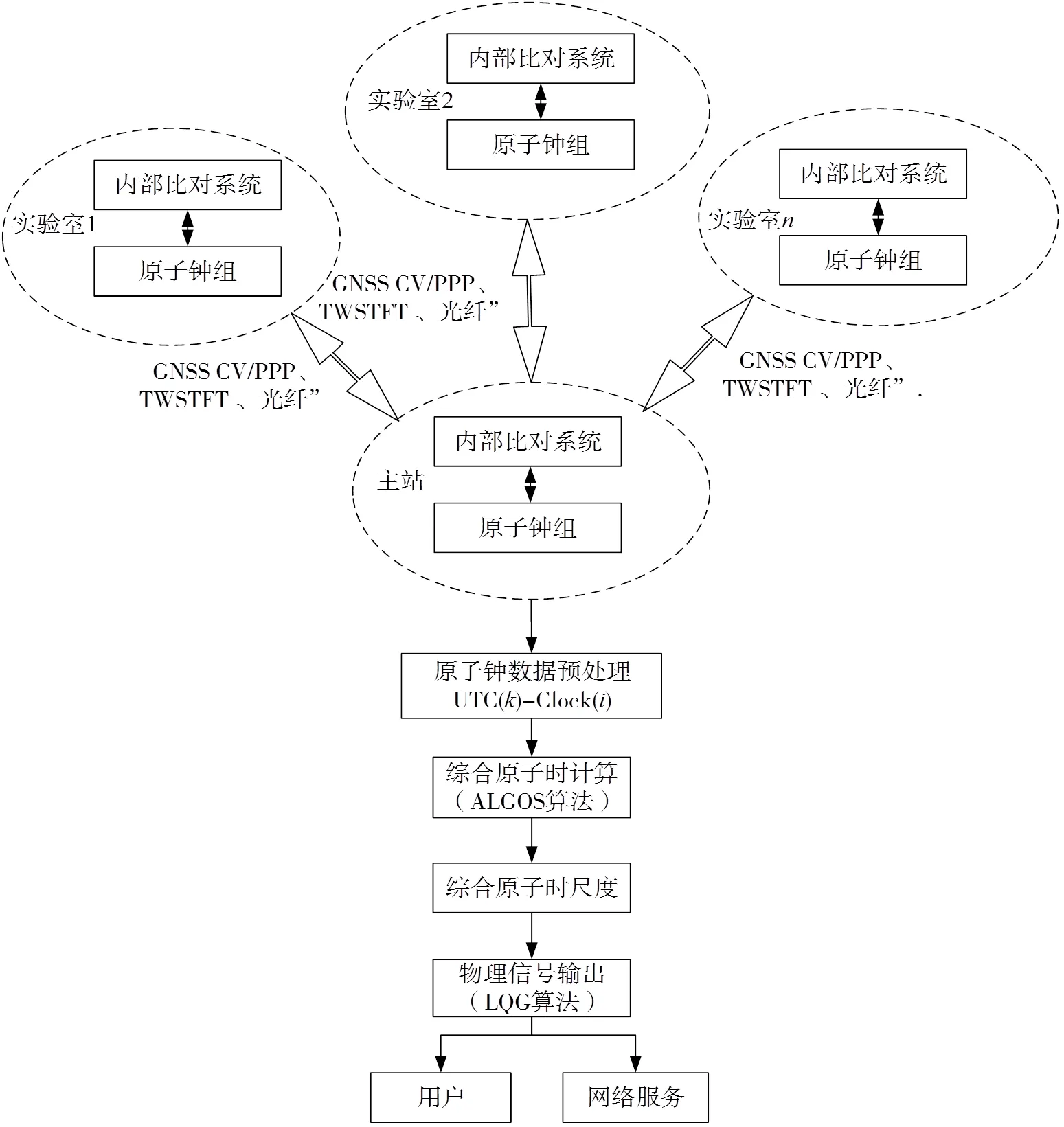
图1 系统组成框图

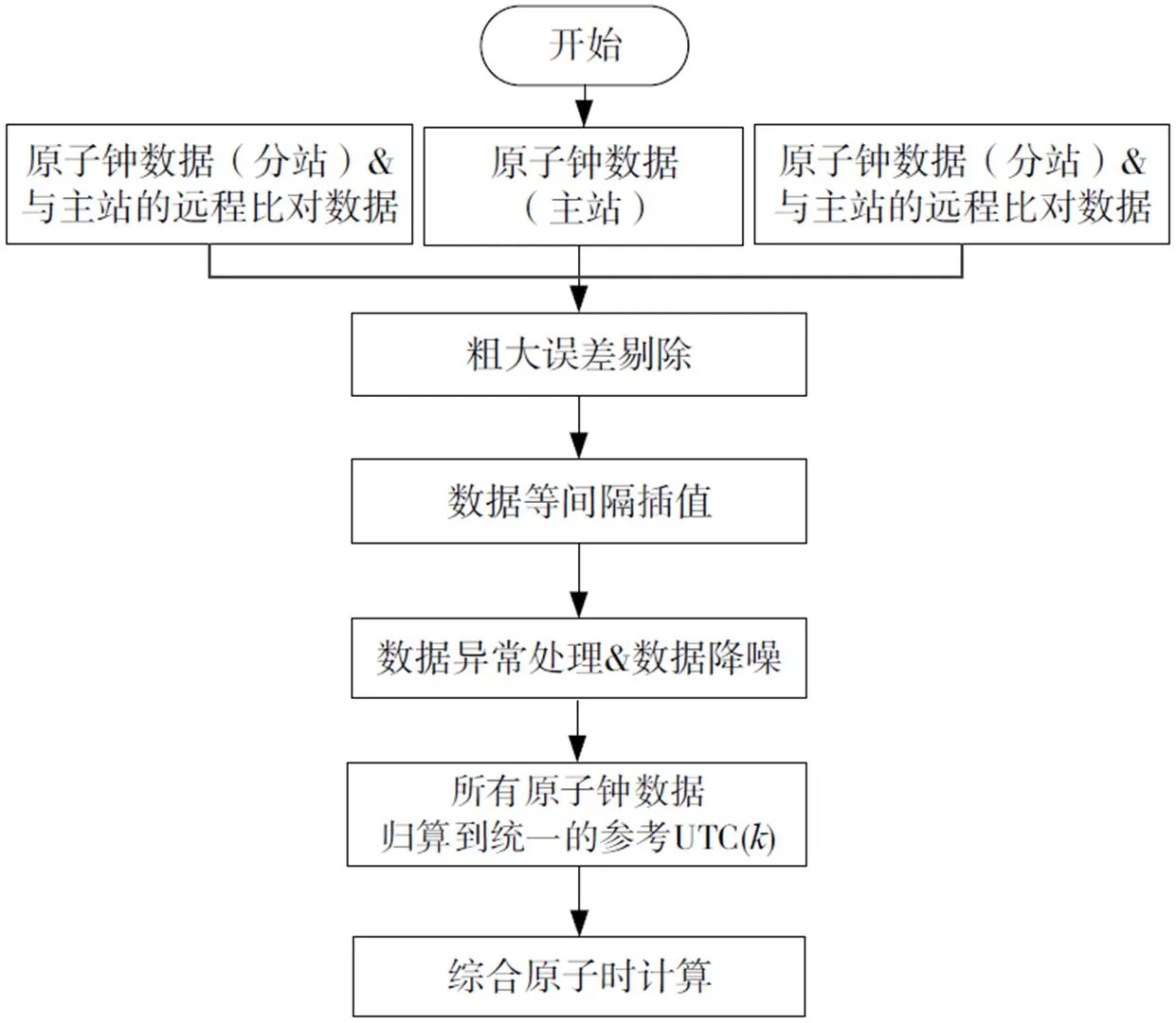
图2 原子钟数据预处理流程

2.2 综合原子时尺度计算

时间尺度作为频率驾驭控制的主要实时参考，对标准时间频率产生的控制精度起到至关重要的作用。氢原子钟和铯原子钟作为两种不同性能的频标，从统计学的角度上来说，它们在短期和长期频率稳定度方面的表现各异。在短期稳定度方面氢原子钟明显优于铯原子钟，虽然近些年氢原子钟在长期稳定度方面有很大提高，但仍存在频率漂移甚至二次漂移[14-16]。

将氢原子钟、铯原子钟分组，经钟差预测、频率估计和权重估计，分别产生氢钟时间尺度TAHM和铯钟时间尺度TACs。这两个时间尺度互为参考，铯钟速率经TAI速率校正后，利用铯钟数据产生的原子时尺度TACs，以及利用铯钟生成的时间尺度TACs将氢钟生成的时间尺度TAHM的长期漂移扣除，综合两者得到稳定度和准确度最优的参考时间尺度TASUM。综合原子时尺度的计算示于图3。

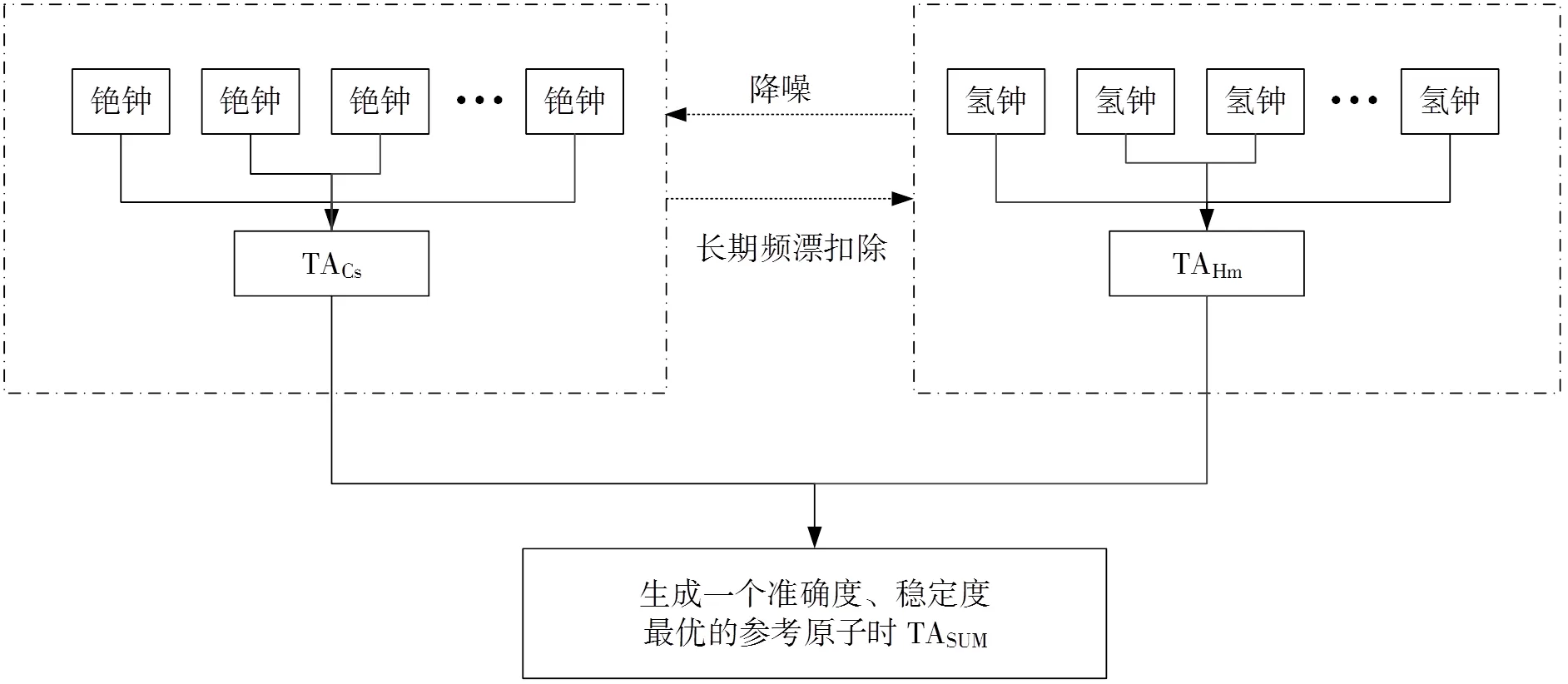
图3 综合原子时尺度的计算

2.3 实际物理信号产生

每台原子钟都可作为一个独立的主钟系统，但原子钟的频率普遍存在偏差和漂移，因此需要对原子钟进行频率调整。为维持原子钟的稳定性，一般不直接对原子钟进行相位或频率的干预，而是通过外部频率调整设备（一般为相位微调仪）实现对原子钟输出信号的修正，不仅需要考虑驾驭后输出信号与标准时间的偏差，还应注意驾驭后信号的频率稳定性。

还需考虑一些特殊情况，当外界环境温度或是其他原因导致的瞬间较大的频率跳变，则必须在短时间内将较大的频率跳变调整到正常频率值附近。由于每小时计算短期参考原子时（reference atomic time，RTA），可以实时监测主钟输出信号是否发生异常，并由此给出是否需要立即进行“临时性”的频率驾驭。

目前最常用的频率驾驭算法是最小二乘估计方法，经过长期试验发现，该方法没有很好消除噪声影响，且易受异常数据和异常信号的影响。最优二次型高斯控制算法（linear quadratic gaussian control，LQG），利用最小化二次代价函数不断地逼近最优控制，再通过Kalman滤波方法，构造增益矩阵的递推公式，将控制值和滤波器不断迭代直至收敛，并且考虑驾驭强度和驾驭周期，最终计算得到最优的频率驾驭量。

为了进行异地多站联合守时方法研究，在不干扰当前实验室内守时系统的工作前提下，搭建实验系统并开展相关实验，在临潼主站建立一个UTC（Test）监测与控制实验系统（包括硬件系统、软件系统），并利用该实验系统进行相关研究。

1）硬件系统

UTC（Test）监测与控制实验系统的硬件部分包括一台HROG-5相位微调仪（分别用作主钟频率源的频率驾驭）、一台计数器和一个工控机，硬件结构图如图4所示。从时频基准实验室引出实验系统的主钟频率源（氢钟）频率信号，经相位微调器进行频率驾驭后，输出1 PPS信号，接入计数器与UTC（NTSC）进行比对，比对结果输出到工控机，用于监测与控制UTC（Test）方法的研究。

图4 硬件结构图

2）软件系统

软件是实现异地多站联合守时的关键，在UTC（Test）监测与控制实验系统中，软件的功能主要包括：

① 数据采集、管理及数据预处理

采集异地多站的原子钟比对数据、溯源比对数据、BIPM最新的CirT公报、以及最新的速率和频漂公报；各种数据格式的检查等。

② 利用ALGOS算法，计算产生综合原子时尺度TA。

③ 以综合原子时尺度TA为参考，对主钟进行频率驾驭，实现实际物理信号产生。

④ 根据实验结果进行分析，分析和验证异地多站联合守时的效果。

3 测试结果与分析

实验时间选择2021年1月1日（MJD = 59 215）至2021年4月1日（MJD = 59 305），采用国际标准时间产生（TAI/UTC）的模式，搭建综合原子时比对网络，将西安场区、蒲城场区和临潼场区的原子钟数据，以及各场区间的溯源比对数据传递至临潼主站，由临潼主站计算异地联合时间尺度TA。以临潼和西安为例，采用相同的时间尺度TA作为驾驭参考，对主钟频率源进行驾驭，分别实现了实时物理信号产生。以联合时间尺度TA和协调世界时UTC为参考，对临潼和西安产生的实时物理信号UTC（Test）的性能进行评估。

利用GPS CV远程比对方法，计算出临潼场区系统时间与蒲城场区系统时间的共视比对结果，并利用Vondrak平滑方法以及交叉证认法确定平滑因子，对共视比对结果进行平滑。共视比对结果和其平滑结果如图5所示。对溯源结果和平滑结果进行稳定度分析，可以看出平滑结果的短期稳定度得到了明显的提高，这主要因为Vondrak平滑方法消除了溯源结果中部分相位白噪声，如图6所示。

利用光纤比对方法，计算临潼场区系统时间与西安场区系统时间的光纤比对结果，并利用Vondrak平滑方法以及交叉证认法确定平滑因子，对光纤比对结果进行平滑。光纤比对结果和其平滑结果如图7所示。对光纤比对结果和平滑结果进行稳定性分析，可以看出，平滑结果的短期稳定度得到了明显的提高，这主要因为Vondrak平滑方法消除了溯源结果中部分相位白噪声，如图8所示。同时，相比于GNSS共视方法，光纤比对链路的不确定度优于共视链路一个量级以上。如果有更高精度的原子钟如铯喷泉钟、光钟等参与异地联合守时，建议采用更高传递精度的光纤比对链路，才能保障高精度原子钟的精度不受链路传递的影响。

图5 临潼场区与蒲城场区系统时间的共视比对结果以及平滑结果

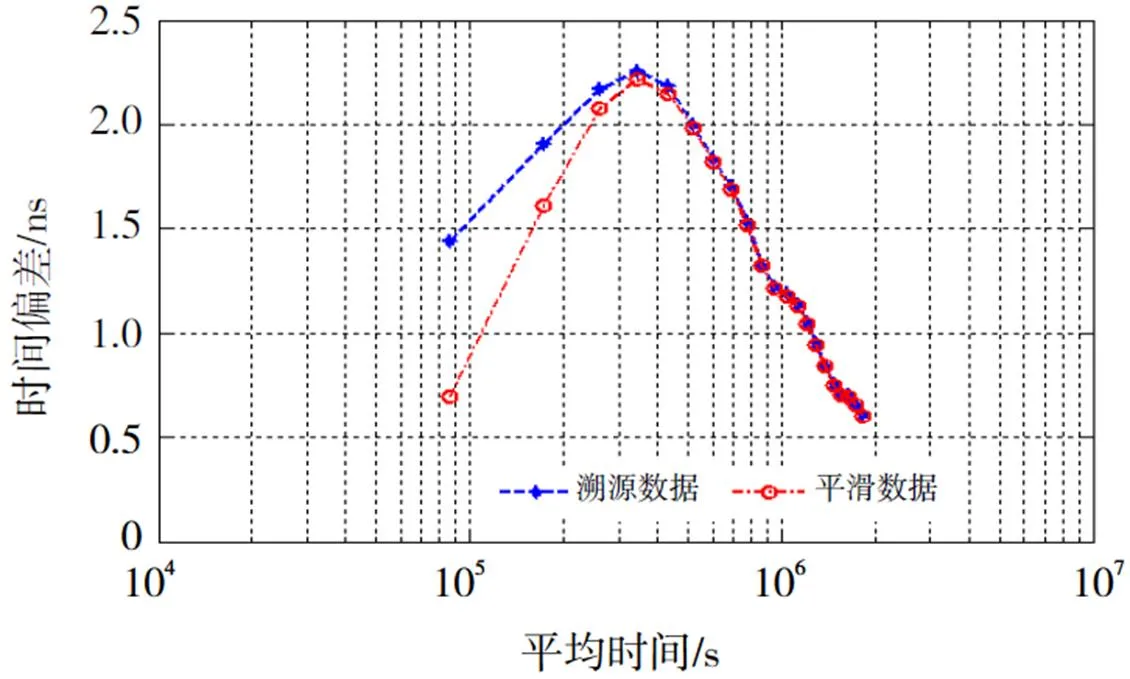
图6 临潼场区与蒲城场区系统时间的共视结果以及平滑结果的时间方差

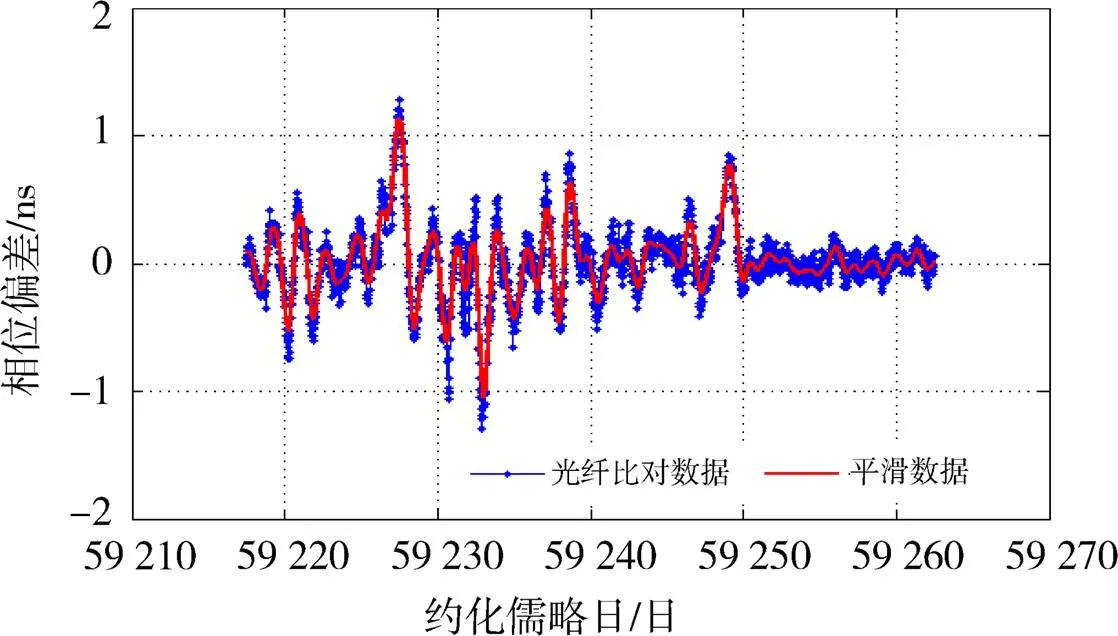
图7 临潼场区与西安场区系统时间的光纤比对结果以及平滑结果

采用综合原子时比对网络和远程比对链路，将蒲城场区以及西安场区的原子钟数据参考到临潼主站的UTC（NTSC）上。利用ALGOS算法，计算获得联合时间尺度TA。

标准时间产生的试验分别在临潼场区和西安场区开展。以临潼场区为例，选择临潼场区的一台氢钟（型号为MHM-2010）作为主钟，以联合时间尺度TA作为驾驭参考，采用LQG方法，驾驭产生标准时间UTC（Test）LT。在西安场区采用相同的方式，其驾驭产生的是标准时间UTC（Test）XA。采用的原子时算法和频率驾驭算法相同，其结果的差异主要受主钟的性能不同，以及驾驭算法中参数设置不同等因素影响。

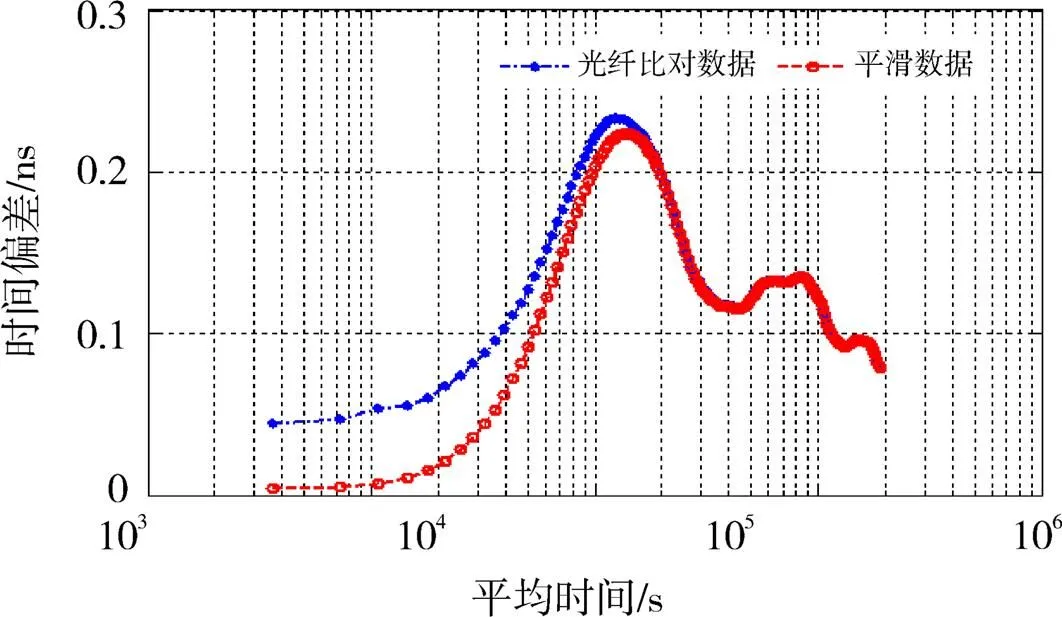
图8 临潼场区与西安场区系统时间的光纤比对结果以及平滑结果的时间方差

从图9可以看出，联合时间尺度TA与标准时间UTC（Test）LT，以及联合时间尺度TA与标准时间UTC（Test）XA的相位偏差均保持在±5 ns以内。相比于TA，UTC（Test）LT相位偏差的均值为1.29 ns，其标准偏差为0.7 ns，而UTC（Test）XA相位偏差的均值为1.45 ns，其标准偏差为1.12 ns。

图9 TA与UTC（Test）LT、TA与UTC（Test）XA的相位偏差

通过本地测量设备，获得UTC（NTSC）与UTC（Test）LT的相位偏差，结果如图10所示。以协调世界时UTC为参考，综合计算得到UTC与UTC（Test）LT，以及UTC与UTC（Test）XA的相位偏差。并利用Allan方差，分析UTC（Test）LT和UTC（Test）XA相比于UTC的稳定度结果，结果如图11和表1所示。

实验结果表明，异地多站联合守时产生的标准时间UTC（Test）LT与UTC（NTSC）的相位偏差小于3 ns。利用远程国际比对链路和临潼-西安的溯源比对链路，分别计算出UTC（Test）LT与UTC（Test）XA与协调世界时UTC的相位偏差。UTC（Test）LT与UTC的相位偏差小于3 ns，其标准偏差为1.19 ns，并且UTC（Test）LT相对于UTC，5d频率稳定度为1.6×10-15，20 d频率稳定度为8.6×10-16。UTC（Test）XA与UTC的相位偏差小于3 ns，其标准偏差为1.32 ns，并且UTC（Test）XA相对于协调世界时UTC，5 d频率稳定度为2.48×10-15，20 d频率稳定度为1.72×10-15。西安场区和临潼场区均采用氢原子钟做主钟，采用联合时间尺度TA作为驾驭参考，频率驾驭算法采用LQG算法，最终西安和临潼场区产生的标准时间性能接近。

图11 UTC与UTC（Test）LT、UTC与UTC（Test）XA的的相位偏差

表1 UTC（Test）LT与UTC（Test）XA的稳定度结果分析

综上所述，异地多站联合守时不仅可以实现多站点的原子钟资源整合，而且提高异地多站联合产生的标准时间性能。同时，采用异地多站联合守时方法研究，实现异地多站复现的物理信号一致性。

4 结语

本文基于国家授时中心的多场区和多远程比对链路，开展了异地多站联合守时方法的研究与实验验证。采用国际标准时间产生（TAI/UTC）的模式，蒲城场区、西安场区将原子钟数据和链路数据传递至临潼，在临潼处理中心统一处理并归算出综合时间尺度。各场区以该综合时间尺度为驾驭参考，最终实现各场区的高精度物理信号产生。

实验结果表明该方法可以有效解决部分站点由于原子钟的个数少，难以形成准确、独立的原子时尺度。通过异地多站联合的方式形成综合时间尺度，不仅可以提高各站点的守时能力，而且通过数量更多的钟加入，可以提高综合时间尺度的稳定性和可靠性。并以此作为驾驭参考，可以在任何站点实现高精度标准时间的产生。该研究内容为后续“高精度地基授时系统”的异地多站联合守时做好前期的理论验证。

[1] PANFILO G, HARMEGNIES A, TISSERAND L. A new prediction algorithm for the generation of International Atomic Time[J]. Metrologia, 2012, 49(1): 49-56.

[2] PETIT G. Towards an optimal weighting scheme for TAI computation[J]. Metrologia, 2003(40): 252-256.

[3] GALLEANI L, SACERDOTE L, TVELLA P, et al. A mathematical model for the atomic clock error[J]. Metrologia, 2003(40): 257-264.

[4] PANFILO G, TISSERAND L, HARMEGNIES A. A new weighting procedure for UTC[J]. Metrologia: International Journal of Scientific, 2013: 652-653.

[5] 赵书红. UTC(NTSC)控制方法研究[D]. 西安: 中国科学院国家授时中心, 2015.

[6] 丁月蓉, 郑大伟. 天文测量数据的处理方法[M]. 南京: 南京大学出版社, 1990.

[7] 赵铭. 观测序列最佳平滑度的确定和精度的估计[J]. 天文学报, 1985, 26(1): 28-33.

[8] KOPPANG P, LELAND R. Linear quadratic stochastic control of atomic hydrogen masers[J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 1999: 517-522.

[9] GÖDEL M, FURTHNER J. Robust ensemble time onboard a satellite[C]//Proceedings of the 2017 International Technical Meeting of The Institute of Navigation, 2017: 26-43.

[10] 白杉杉, 董绍武, 赵书红, 等. 主动型氢原子钟性能监测及评估方法研究[J]. 天文学报, 2018, 59(6): 56-1～11.

[11] BAI Shan-shan, ZHAO Shu-hong, DONG Shao-wu, et al. Joint time scale algorithm of UTC(NTSC) and UTC(SU)[J]. European Frequency and Time Forum & International Frequency Control Symposium (EFTF/IFC), 2018: 197-201.

[12] RILEY W J. Algorithms for frequency jump detection[J]. Metrologia, 2008, 45(6): 154-1161.

[13] 赵书红, 广伟, 袁海波, 等. Vondrak 平滑因子最佳确定方法及在时间比对数据中的应用[J]. 时间频率学报, 2015, 38(1): 21-29.

[14] FARINA M, GALLEANI L, TAVELLA P, et al. A control theory approach to clock steering techniques[J]. IEEE Transactionsons on Ultrasonics, Ferroelectrics and Frequency Control, 2010: 2257-2270.

[15] ZHAO Shu-hong, DONG Shao-wu, QU Li-li, et al. A New strategy for UTC(NTSC) based on hydrogen clock[C]//Proceedings of the 2016 IEEE International Frequency Control Symposium(FCS), 2016: 227-231.

[16] ZHAO Shu-hong, YIN Dong-shan, DONG Shao-wu, et al. A new steering strategy for UTC(NTSC)[C]//Proceedings of the 2014 IEEE International Frequency Control Symposium (FCS), Taipei: IEEE, 2014: 210-213.

Research on multi-station joint timekeeping method

ZHAO Shu-hong1,2, DONG Shao-wu1,2,3, YUAN Hai-bo1,2,3,BAI Shan-shan1,2, QU Li-li1,2, LI Xiao-hui1,2,3

(1. National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China;2. Key Laboratory of Time and Frequency Primary Standards, Chinese Academy of Sciences, Xi’an 710600, China;3. University of Chinese Academy of Sciences, Beijing 100049, China)

For the multi-station joint timekeeping method, on one hand, the limited atomic clock resources can be integrated to improve the utilization rate of atomic clocks, and all the involved atomic clocks can contribute to ultimate time scale, the stability and accuracy of joint time scale can be improved. On the other hand, the joint time keeping can provide a more stable and reliable steering reference, which can effectively improve the performance of real-time output physical signals in various laboratories. Based on the advantages of the multi-stations and multi-comparison links in the National Time Service Center, a real-time physical signal generation experiments were carried out in Pucheng, Lintong and Xi’an respectively, the joint time scale TA were calculated by using the atomic clock data of those stations, and the master clocks in Xi’an and Lintong were steered using this time scale as a reference respectively. Finally, the time differences between UTC and the real-time physical signals generated by stations of Xi’an and Lintong are all keeped within ±3 ns. The experiments shown that the use of the multi-station joint timekeeping method can achieve the consistency performance of physical signals reproduced by different stations.

joint time scale; frequency steering; ALGOS algorithm; linear quadratic Gaussian control algorithm

10.13875/j.issn.1674-0637.2021-04-0288-12

赵书红, 董绍武, 袁海波, 等. 异地多站联合守时方法研究[J]. 时间频率学报, 2021, 44(4): 288-299.

2021-04-29；

2021-06-21

国家自然科学基金面上资助项目（11773030）；西安重大科技创新平台资助项目（20191722615KYPT017JC019）