基于二自由度PI控制的PMSM的参数整定研究
黄新成,简炜,陈宇峰,张金亮,彭国生,李艺仁
(湖北汽车工业学院电气与信息工程学院,湖北 十堰 442002)
近年来随着科技的不断发展,永磁同步电机(permanent magnet synchronous motor,PMSM)因结构简单、效率高等优点广泛应用在工业控制领域,且永磁同步电机的控制算法也成为了研究热点[1]。目前市面上大多控制方法是使用id=0的双闭环PI控制的矢量控制策略。对于PMSM调速系统这种高性能控制系统来说,常规的PI控制只能设定一组参数,难以同时兼容良好的转速响应能力和扰动抑制能力。为了克服这种工业控制系统所共有的矛盾问题,科研人员提出一种二自由度(two degree-of-freedom,2DOF)控制方法,即采用适当的结构解耦方法,对快速响应能力和抗扰能力设计独立的控制器,得到两种特性的最优解,使系统具有良好的闭环特性[2]。2DOF控制既提升了工业控制系统的动态品质,又保证了生产过程的安全和高效[3],所以逐渐被应用在工业控制等各个地方[4-10]。
文献[4]针对不稳定时滞过程,在内模控制的基础上提出一种2DOF Smith预估控制方案,将设定值响应和抗扰动响应完全解耦,大大提高了系统的稳定性。文献[5]针对称重送料机在广义最小方差控制(generalized minimum variance control,GMVC)的基础上设计一个补偿器,2DOF PD控制很好地消除了系统稳态速度误差。文献[6]通过考虑PMSM的非线性动力学模型和系统期望平衡点的全局指数稳定性,设计一个前馈型2DOF控制系统使闭环系统收敛,具有非常强的鲁棒性。文献[7]在PMSM转速环输入增加一个滤波器,使用遗传算法对其参数进行优化,并设计状态观测器将负载转矩估算值补偿到电流环,有效地提高了速度环的快速性和抗干扰性。
本文将2DOF控制方法和PMSM的矢量控制法结合起来,提出一种基于误差判断的2DOF PI控制的PMSM控制策略。首先对PMSM电流环的数学模型进行分析并给出参数整定;然后使用多重主导极点法(multiple dominant poleplacement method,MDPM)对转速环PI参数进行调优,并结合着上升时间、超调量等时域性能指标设计了2DOF PI控制器;最后进行仿真和基于模型设计(model-based design,MBD)实现,结果验证了这种方法的有效性。
1 PMSM数学模型
为了简化分析永磁同步电机的数学模型,通常对其进行一定的假设后,便可建立PMSM的数学模型。对于表贴式的PMSM来说,Ld=Lq=Ls,id=0的控制方法最为简便。在d-q坐标系下的表贴式PMSM数学方程如下:

式中:ud,uq分别为定子电压的d,q轴分量;id,iq分别为定子电流的d,q轴分量;R为定子电阻;ωm为实际机械角速度;ωe为电机转子电角速度;Ls为定子电感;Ψf为永磁体磁链;J为机电系统转动惯量;B为阻尼系数;Te为电磁转矩;TL为负载转矩;Kt为电磁转矩常数;pn为极对数。
2 传统PI控制器设计
常规的PMSM矢量控制系统大多采用双闭环控制结构。电流环作为转速环的内环,一般是设计电机控制系统的首要目标[11]。
2.1 电流环控制器设计
在id=0控制策略中,设计电流内环时主要考虑对转矩电流id的控制性能。将定子电压方程进行变换,便可得到PMSM在电流环的等效传递函数:

将数字控制的逆变器部分等效为一阶惯性环节:

式中:Ts为SVPWM环节设置的逆变器开关周期;Td为延迟环节时间常数,考虑到开关、死区、控制等存在的延时,令Td=0.5Ts;KPWM为逆变器增益系数,由于逆变器的输出和给定电压相同,所以KPWM=1。
因为逆变器的开关频率比较高,所以将PWM环节和延迟环节做近似合并处理。电流环调节器采用经典的PI控制,q轴电流环的结构图如图1所示。

图1 q轴电流环结构图Fig.1 The structure diagram of q-axis current loop
在电机控制系统的设计中,电流环的作用主要是以最大电流启动,抑制内部扰动,实现电流的快速跟随。电流环的设计要求是采用零极点对消的方式将其整定成典型Ⅰ型系统。以q轴电流环设计为例,电流环开环传递函数为

式中:K1为电流调节器的比例系数;T1为积分时间常数。
利用PI调节器的零点来对消掉控制对象的极点,则T1=Ls/R。典型Ⅰ型系统的开环传递函数为

通过与典型二阶系统作对比得到K=K1/Ls,T1=1.5Ts。实际工程设计中考虑到二阶系统的各项性能指标,系统的阻尼比通常选取0.707,即KT=0.5,便可得到电流环调节器的PI参数:

2.2 转速环控制目标
转速环的设计是实现控制系统拥有优良调速性能的关键点,能够减少转速波动和受外部干扰的影响,提高动态响应速度。由于电流环的采样调节频率比转速环高得多,转速环的截止频率较低且有更高的闭环带宽,所以在分析转速环时可以忽略电流环闭环传递函数的高次项,将其降阶等效成一般的一阶惯性环节[12]:
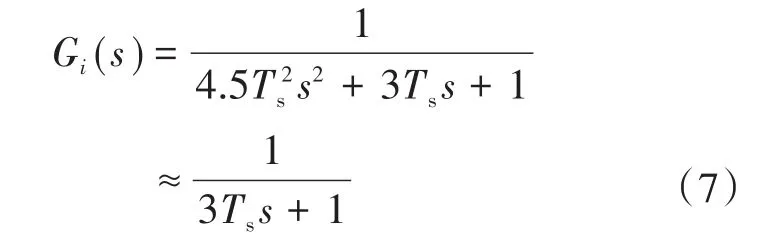
转速环的等效结构图如图2所示。图中,GPI为转速环PI调节器的传递函数;Gi为电流环的等效闭环传递函数;td为转速外环等效延迟环节的时间常数。假设td=Ts,同电流环一样,将延迟环节和电流环闭环传递函数做近似合并处理。

图2 转速环结构图Fig.2 The structure diagram of speed loop
结合图2,便可以得到转速外环控制对象的等效传递函数:
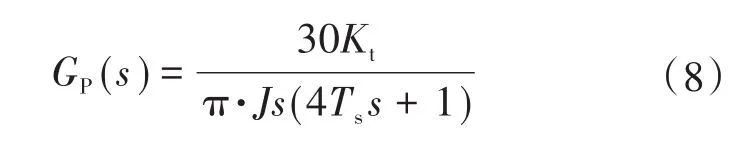
2.3 转速环控制器设计
将PMSM矢量控制系统简化成如图3所示。
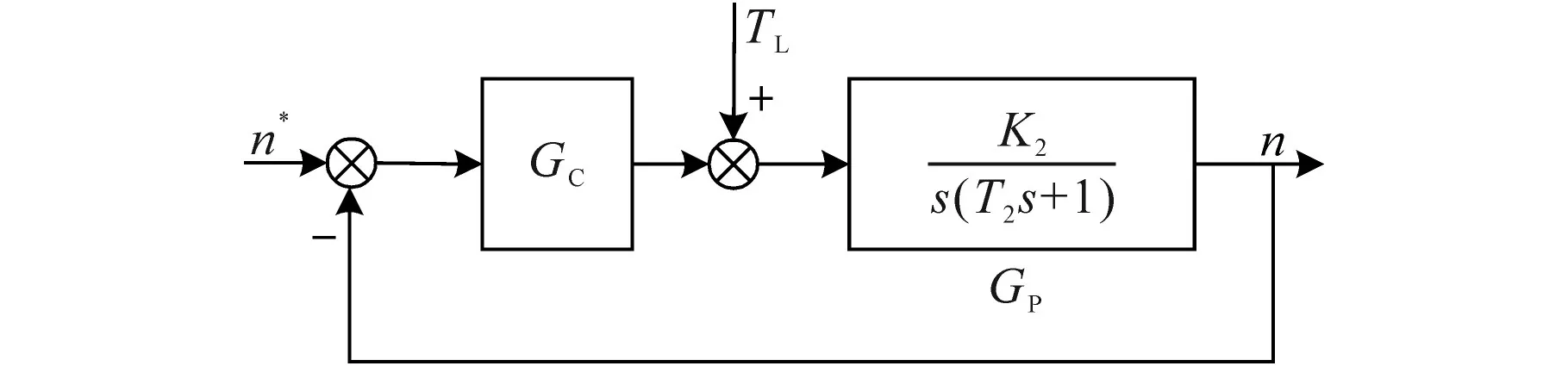
图3 控制系统结构图Fig.3 The structure diagram of control system
图3中,K2为控制对象的等效增益,K2=30Kt/πJ;T2为时间常数,T2=4Ts;GC为标准的PID控制器,如下式:

从式(9)可以看出,当KD=0或者TD=0时,GC就是经典的PI控制器。
转速环PI参数采用MDPM[13]进行整定。MDPM的原理是假设闭环系统存在一个多重稳定的真实主导极点,并且忽略非优势极点和零点对控制过程的影响。结合式(9),得到控制系统传递函数的闭环特征方程N(s):

令N(s)=0,并进行微分可得:
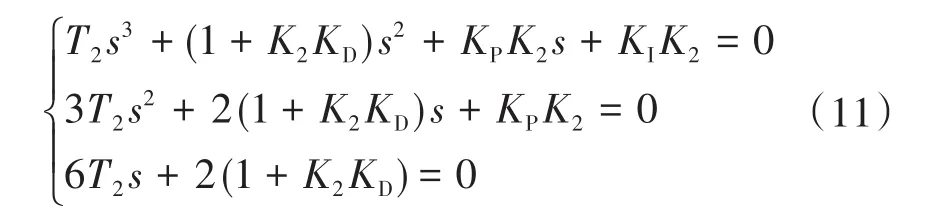
将KD=0代入式(11),可以得到PI控制器的可调参数及三重主导极点:

3 2DOF PI控制器设计
3.1 2DOF控制策略的提出
PMSM是一个非常复杂的控制对象,它的控制系统必须拥有良好的设定值跟随性和抗干扰性能,2DOF控制器可以很好地处理这个问题。2DOF的控制结构有多种,本文在典型的Feed⁃back型二自由度控制结构上做出了改进,提出了基于误差判断的Feedback型2DOF PI控制,其结构如图4所示。
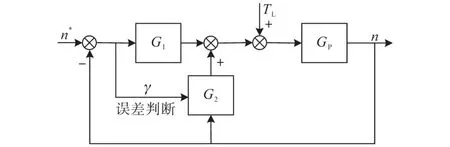
图4 基于误差判断的Feedback型2DOF PI控制结构图Fig.4 Feedback-type 2DOF PI control structure diagram based on error judgment
图4中,GP是控制对象的等效传递函数;由于微分环节的抗噪声干扰能力较弱,所以G1,G2是PI控制器;γ是误差判断环节的判定值。该新型2DOF PI控制结构的闭环表达式为
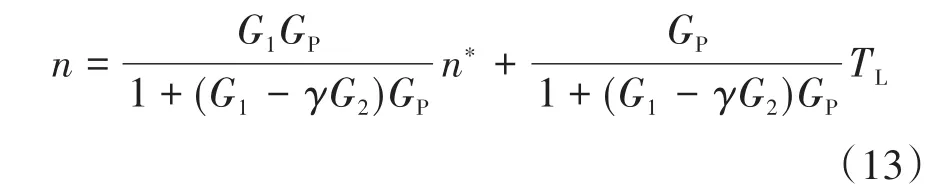
从式(13)中可以看出,两个可调参数控制器G1和G2使得两个闭环传递函数可以分别调整,不仅使控制系统获得良好的抗干扰特性,而且具有灵活的给定值跟踪性能。
3.2 2DOF PI控制器设计
对于图4的控制系统,令Δn=n*-n,其中,n*为期望电机转速,n为电机实际速度,Δn为转速误差值,取:
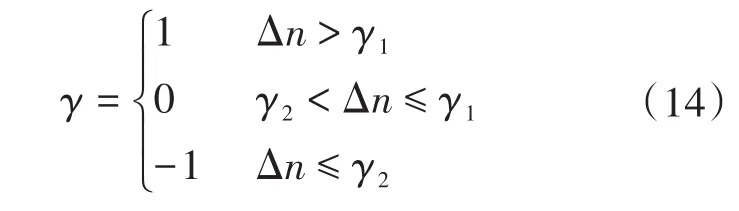
式中:γ1,γ2为误差判断环节的上、下界限值,且γ1> 0,γ2< 0。
设G1(s)= δ+ μ/s,G2(s)= δ1+ μ1/s,则有:
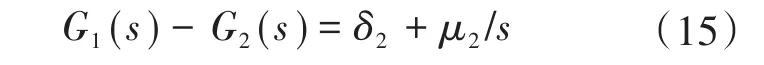
其中

式中:δ,μ,δ1,μ1分别为G1,G2的PI系数,δ和μ为已知值。
1)当Δn>γ1时,电机实际转速低于期望速度,此时系统反馈的信息应该促进并加强控制环节的动作,G2应该是正反馈。
首先,考虑到控制系统的抗干扰特性,列出扰动传递函数如下:
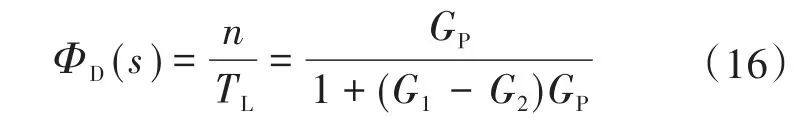
通常TL为阶跃信号,即TL=Q/s,Q为幅值。由终值定理推导可得:
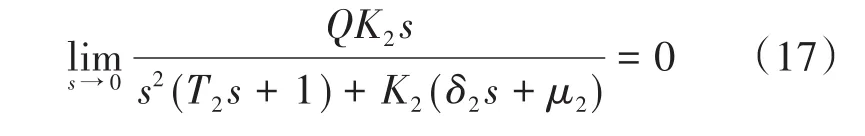
式(17)表明,2DOF PI控制系统的扰动传递函数是一个三阶传递函数,且当系统趋于稳定的工况下,给定扰动TL对控制系统的影响趋于0,说明所设计的控制系统有一定的抗干扰能力。
其次,在实际工程应用分析中,对于高阶系统一般都用二阶系统去近似处理。前提是高阶系统的所有零极点都在左半平面,且具有1对距离虚轴较近的共轭复数极点,也称共轭复数主导极点[14]。假定系统有3个闭环极点:s1,2=-x±jy,s3=-z,且x,y,z>0,从扰动传递函数可得系统的闭环特征多项式F(s)为

根据配置的极值点,得到期望特征多项式如下:
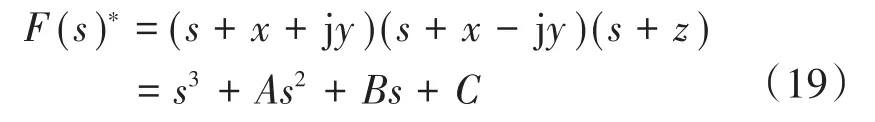
比较式(18)和式(19)的各对应项系数,可解得:
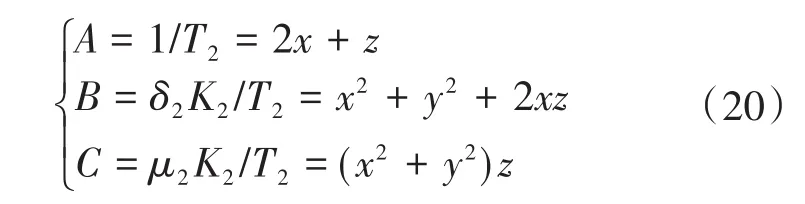
假设z≫x,根据主导极点定义可得:若高阶系统的共轭复数主导极点的实部是其他极点实部的1/5或者更小,则控制系统可以等价二阶系统进行频域响应分析。先忽略极点s3的作用,将系统闭环特征方程改写成二阶标准形式:
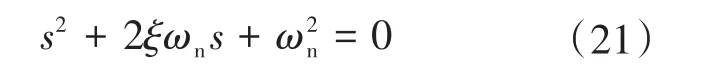
式中:ξ为系统阻尼比,0< ξ< 1;ωn为无阻尼自然震荡角频率。
期望极点的位置必须根据系统的性能指标来推算确定。选择阻尼比ξ和典型性能指标上升时间tr作为配置极点的条件,则
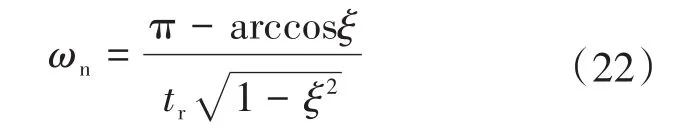
将δ=KP,μ =KI代入,结合式(22)得:
2)当γ2<Δn≤γ1时,电机实际转速稳定在一定的范围内,控制系统为传统的单自由度PI控制。
3)当Δn≤γ2时,电机实际转速高于期望速度,此时系统反馈的信息应该反向调节控制环节的动作,G2应该是负反馈。具体推导过程同步骤1),最终结果为
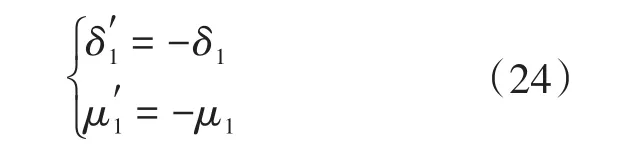
4 仿真及分析
为了验证本文所提出的基于误差判断的2DOF PI控制的有效性,在Matlab/Simulink平台上搭建了永磁同步电机双闭环控制系统的仿真模型。实际控制对象的电机参数如表1所示。
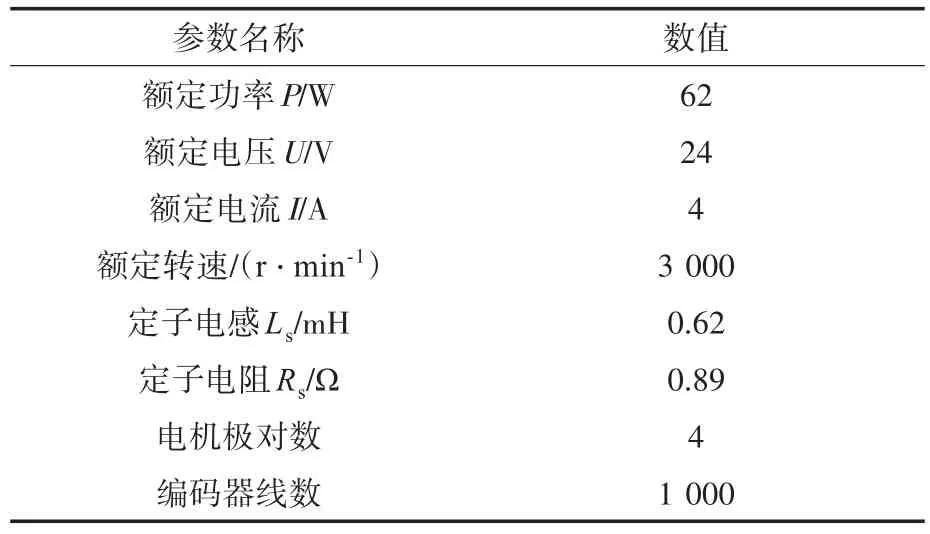
表1 电机参数Tab.1 Motor parameters
对于二阶系统,选择最佳阻尼比ξ=0.707,取上升时间tr=10 ms,误差界限值γ1=γ2=10,然后对不同的控制策略在相同的转速指令和突增负载下进行仿真。为了测试系统的动态响应和稳态响应,设置了阶段性给定转速,在t=0时,系统给定速度为2 000r/min;在t=0.1s时,给定转速下降为1 000r/min;并且在t=0.2 s时,加上负载转矩10 N·m。速度响应波形如图5所示,负载转矩波形如图6所示。

图5 速度响应波形Fig.5 Speed response waveforms

图6 负载转矩波形Fig.6 Load torque waveforms
仿真实验使用三组控制策略进行对比:文献中使用常规控制整定方法得到的单自由度PI参数;本文中使用多重极点配置法得到的单自由度PI参数;所提出的2DOF PI参数。根据图5的速度响应波形分析得到的仿真性能指标对比结果如表2所示。

表2 仿真性能指标对比结果Tab.2 Simulation performance index comparison results
通过图5和表2的结果可以看到,本文所提出的单自由度PI控制系统虽然在速度响应能力上强于传统PI控制系统,但两个系统的抗扰能力是相差无几的;而本文所提出的基于误差判断的2DOF控制无论是在外部扰动抑制性能和目标转速跟踪性能方面,这5个时域系统性能指标的值都远远优于其他两组参数所得到的仿真结果。图6为仿真转矩比较波形,在电机升降速的过程中,相比于其他两个系统,2DOF控制系统具有更好的动态性能;在0.4 s时突加一定的负载转矩,2DOF控制系统能很快地适应负载力,超调转矩较小,具有更快的动态加载特性。
5 实验及验证
5.1 硬件实现
为了验证2DOF PI控制的可行性,搭建了以DSP28335芯片为核心的硬件控制系统对其进行验证。硬件系统如图7所示。整个硬件系统由直流24V驱动电源、驱动模块、控制电路、个人电脑以及目标电机等几部分组成。图7中,编码器采用增量式光电编码器,ia和ib为传感器采集的相电流。
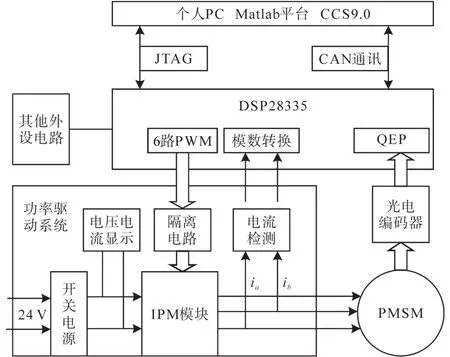
图7 硬件系统Fig.7 Hardware system
5.2 实验结果
本文使用MBD自动生成嵌入式代码[15]的实现方式,首先在Simulink中建立控制系统模型,在参数配置中选择相应的底层配置和编译环境,并在模型搭建过程中使用IQmath模块将数据交互有机统一起来,最后生成嵌入式c代码到CCS9.0中,烧写进DSP28335控制目标电机运行,目标电机参数与表1所示参数一致。传统PI控制系统实验结果如图8所示,2DOF PI控制系统实验结果如图9所示。
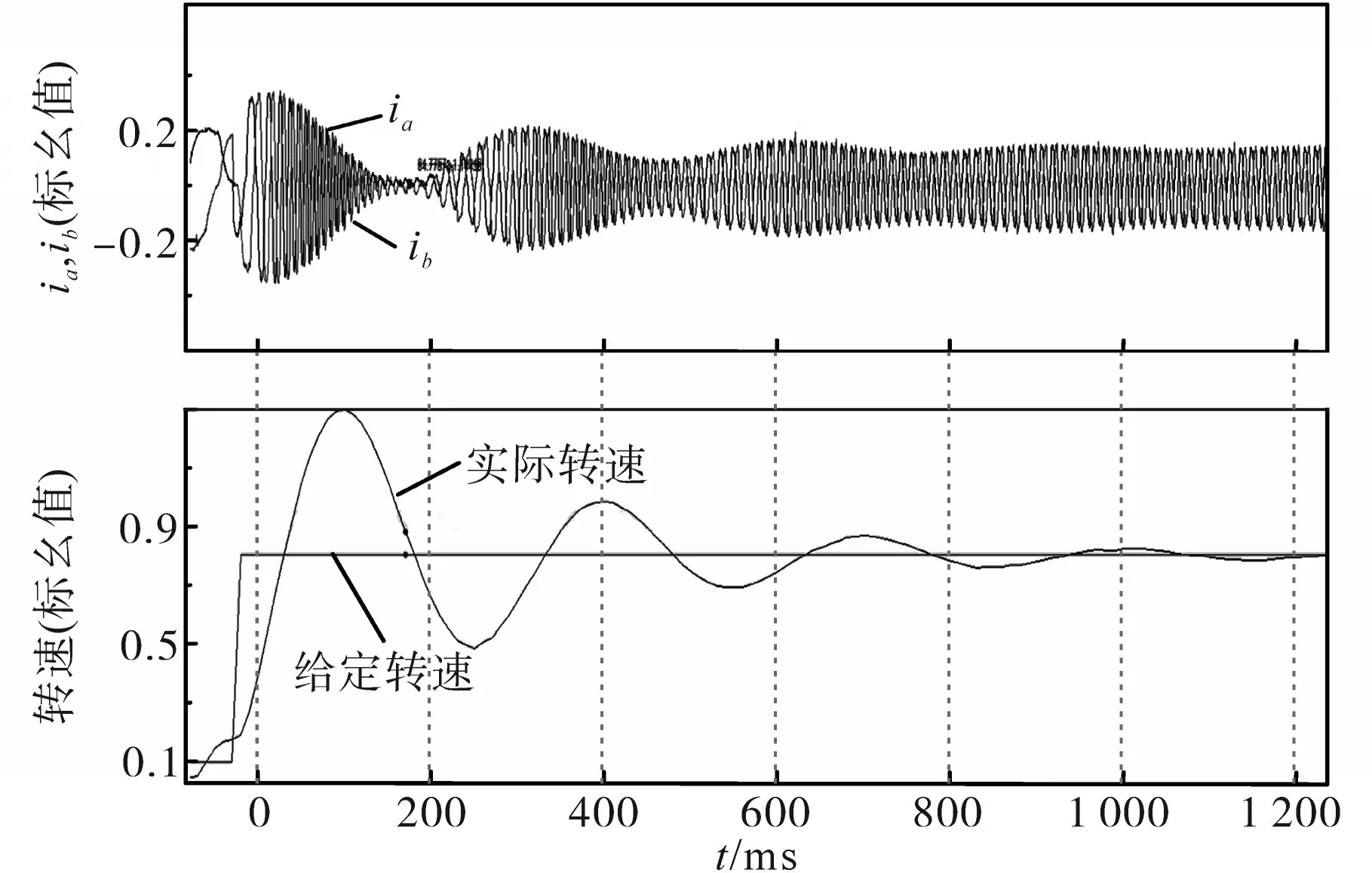
图8 传统PI控制系统实验结果Fig.8 Experimental results of traditional PI control system
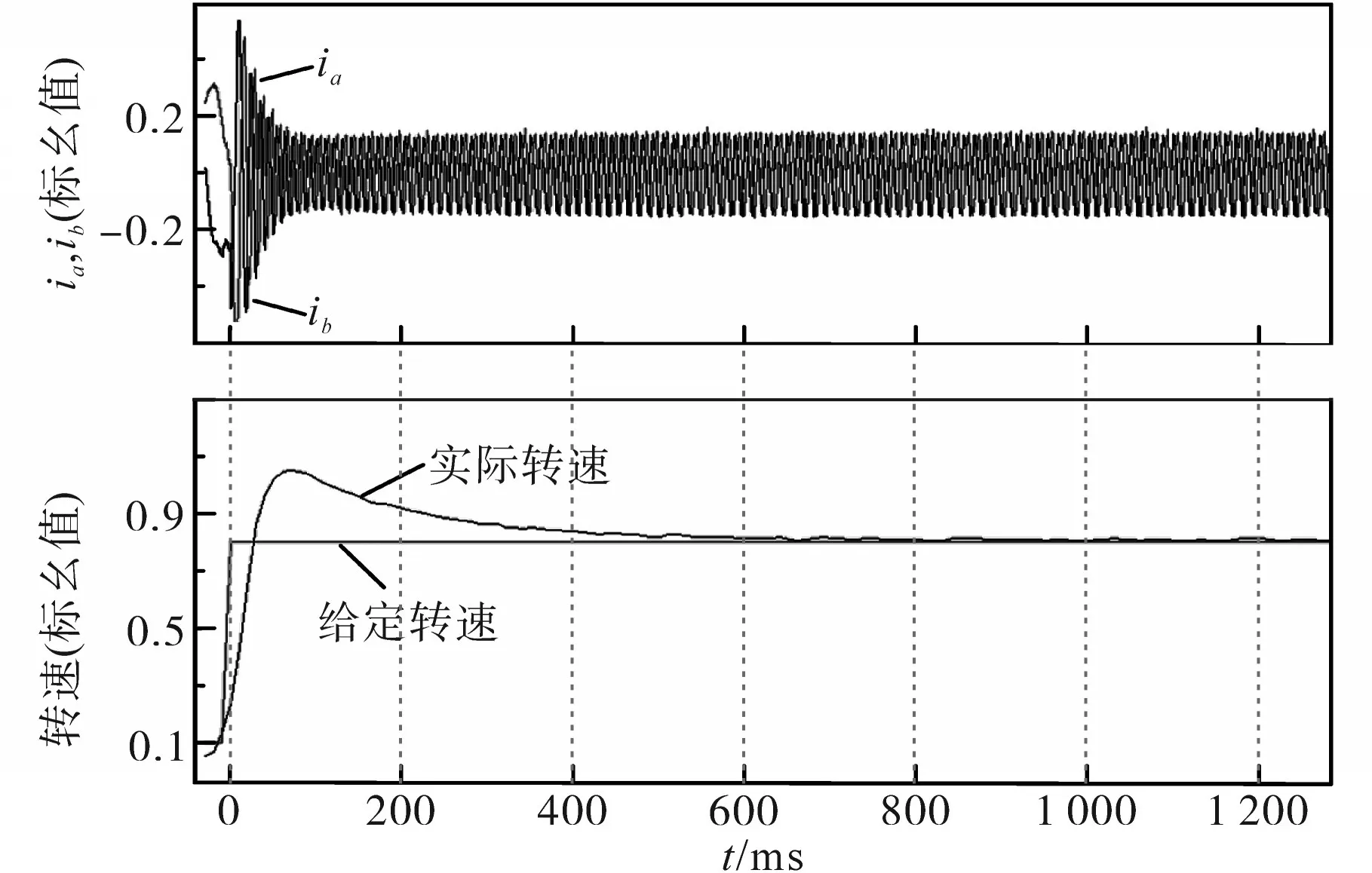
图9 2DOF PI控制系统实验结果Fig.9 Experimental results of 2DOF PI control results
本文使用基于CAN通讯的控制系统调试方式,将采集到的两相电流数据和计算的速度信息通过eCAN模块发送到CANpro工具中,经过解析后呈现实时数据显示。在搭建模型时采用数据类型变换将模型内所有数据信息进行标幺化设置[16]。硬件系统采用三电阻法进行电流采样,采样范围为±1A。因为PMSM控制系统是一个高阶复杂的非线性系统,所以将仿真中按照线性系统设计的控制参数应用到实际中得到的结果会有一些不同。
本次实验中设定电机转速为0.8(标幺值),即2 400r/min,电机空载运行。如图8所示,传统PI控制的电机系统给定转速响应差,电流波动较大,对电流环造成比较大的负荷,系统上升时间为0.06 s,最大超调量达到64.3%,且存在较长的振幅抖动现象,调整时间为1.05 s。与传统PI相比,2DOF控制应用到实际系统中有更好的控制效果,系统上升时间为0.02 s,最大超调量为29.2%,系统没有振荡运动,波形较为平滑,调整时间为0.5 s,且电流波动较小。相比之下,2DOF PI控制的PMSM调速系统具有更好的动、静态性能和强鲁棒性。
6 结论
本文将2DOF控制思想引入到交流PMSM控制系统当中,先将电流环进行参数整定和模型简化,然后对转速环PI参数进行调优,最后根据时域分析法求得2DOF PI参数。在传统PI控制的基础上简单改进,解决了单自由度PI控制不能兼顾指令跟随特性和抗扰动特性的缺点。利用2DOF PI控制可以有效地改善PMSM调速系统的伺服性能,提升系统的鲁棒性,对实际工程应用也有一定的借鉴意义。

