一种虚拟同步发电机的附加阻尼控制策略研究

何伟，熊俊杰，赵伟哲，何昊，李佳，陈拓新

（1.国网江西省电力有限公司电力科学研究院，江西 南昌 330096；2.国网江西省电力有限公司电力调度控制中心，江西 南昌 330077）

近年来，新能源的大规模并网应用，使得传统电力系统中发电单元的构成发生了巨大的变化，深刻改变着电力系统的动态行为[1-3]。由于新能源电力大都需要经过电力电子变换器接入电网，缺乏同步发电机（synchronous generator，SG）的转子惯量支撑，大规模并网后电力系统的频率稳定问题日益突出。

为了解决新能源并网引起的弱惯量问题，借鉴SG的频率运行特性，虚拟同步发电机（virtual synchronous generator，VSG）的控制策略应运而生。文献[4-6]通过对SG转子运动方程的等效模拟来控制逆变器，使其在频率输出特性上与SG的频率响应特性具有一定的相似性。文献[7]对VSG的惯量支撑特性进行了分析，并对比了SG的惯量特性。值得商榷的是，VSG控制的逆变器系统虽然具备了惯量特性，但在并网模式中容易引发系统的不稳定。文献[8-9]指出VSG具备SG惯量的同时，也继承了SG容易引起振荡的风险，在受到扰动时，系统的频率会产生持续的振荡。文献[10-11]分析了VSG虚拟转矩特性及失稳机理。文献[12-13]针对VSG动态特性适应性较弱的问题，提出VSG的惯量自适应控制策略。大量文献研究表明，VSG控制在并/离网运行时所需要的惯量特性并不相同，恒定惯量系数下的VSG控制难以实现不同运行下的惯量需求。文献[14]分析了多机并联系统的振荡问题，并提出通过参数优化的方式来解决该问题，但参数优化对系统结构参数、稳态运行参数的要求较高，适应性较差。文献[15]提出最优响应的VSG控制策略，但切换过程的阈值判断条件并没有给出。文献[16]提出一种自适应虚拟阻抗控制策略，解决中低压阻感线路功率耦合问题，提高了系统的可靠性。自适应虚拟阻抗的实质是强化了有功-频率和无功-电压的耦合关系，减小功率耦合对控制的影响，但阻抗的优化实现较为复杂。文献[17]提出一种适用于微电网系统的转动惯量自适应控制策略，并给出了相关参数的设计原则，但在具体实现中需要实时地判断频率的运行范围，控制的灵活性较差。在以同步发电为主的电力系统中，为了提高系统阻尼能力，抑制低频振荡，通常利用电力系统稳定器（power system stabilizer，PSS）来提高系统的稳定性，因此VSG也可以借鉴PSS的工作原理，通过控制手段来提升VSG系统的稳定能力。

本文在上述文献研究基础上，借鉴SG控制中PSS的运行原理，通过将频率偏差经补偿控制器引入电压控制中构成附加阻尼控制，提高系统的阻尼能力，提升了系统的稳定性。最后，仿真分析验证了本文所提附加控制策略的有效性和正确性。

1 虚拟同步发电机的控制原理

1.1 虚拟同步发电机的结构

VSG的主电路及控制结构如图1所示。系统主电路由逆变器和滤波电路等构成，控制系统由频率-有功、电压-无功控制环节及相应的计算模块构成。主电路中，Udc为直流母线电压；ix（x=a，b，c）为逆变器三相输出电流；ux（x=a，b，c）为 PCC 点三相电压；L，C分别为滤波电感和电容；R为滤波线路电阻。控制电路中，Pref，Qref分别为有功、无功功率给定值；J为VSG系统的转动惯量常数；Dp，Dq分别为频率、电压下垂控制系数；K为控制常数；e为输出电压指令；Mf为模拟励磁系数；if为励磁电流；Un，ω0分别为额定电压和频率；U为VSG输出电压；θ为输出相角；s为微分算子。

图1 VSG主电路及控制系统结构Fig.1 Circuit and control system structure of VSG

根据图1，以a相为例可以得到VSG的电磁方程为

根据文献[4]可以得到VSG的定子与转子间的电气与磁链关系为

其中

式（2）描述了励磁电压与VSG输出端电压关系[4-6]。

1.2 VSG的频率-有功和电压-无功控制

VSG模拟了SG的下垂特性，通过阻尼来反映频率-有功下垂特性，如下式：

式中：ΔTe，ΔP，Δω分别为电磁转矩、有功功率及角频率增量。

同理，电压-无功下垂特性通过引入Dq到控制中，实现电压的调节，如下式：

式中：ΔQe，ΔU分别为无功功率和电压增量；Q%，U%分别为无功功率变化和电压变化百分比。

VSG的控制原理在于通过模拟SG的运行特性，使得逆变器具有了与发电机相似的运行特性，并通过在控制中引入频率和电压的控制，实现了逆变器在稳定频率和电压的同时，也提高了微电网的稳定性（VSG的详细数学模型可参考文献[4-6]）。

2 VSG的附加阻尼控制策略

2.1 虚拟惯量对VSG输出特性的影响分析

根据电力系统中发电机的小信号建模原理，可以得到VSG控制作用下的逆变器系统频率-有功的小信号分析模型。VSG的给定功率与输出功率传递函数为

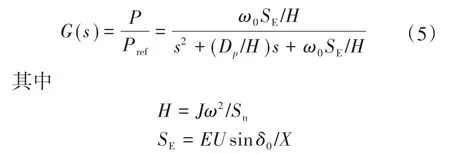
式中：H，SE分别为系统的等效惯性时间常数和同步功率系数；E，U，Sn，X分别为逆变器和电网电压及系统总容量和线路阻抗；δ0为稳态功率因数角。

在不考虑VSG电压耦合的影响时，根据式（5）的传递函数，可以得到频率-有功控制环路的等效小信号框图如图2所示。

图2 系统等效小信号模型Fig.2 System equivalent small signal model

为了直观地体现惯量系数J对系统频率特性的影响规律，图3为不同惯量系数变化时对系统频率响应的影响曲线。

图3 转动惯量变化时VSG的输出频率特性Fig.3 Output frequency characteristics of VSG when the moment of inertia changes

图3中，Nadir为频率曲线最低点。从图3中可以看出，随着J的增大，系统的惯量增大（对应等效惯性时间常数H增大），在受到扰动时，频率的变化率及最低点有所改善，但是振荡时间明显变长。在实际电力系统运行中，频率振荡时间过长可能触发频率解列装置保护动作，威胁系统的安全稳定运行。

为了提高VSG的动态性能，希望VSG在并网时能够具备较大的阻尼作用，在不影响系统出力的情况下提高系统的动态性能。为此借鉴SG系统中的PSS原理，将频率偏差引入到电压控制中形成附加阻尼控制系统，以改善系统的阻尼能力，提高系统的频率稳定性。

2.2 VSG的附加阻尼控制原理

在电力系统中，一般通过加装PSS来提高SG的阻尼特性[18]，PSS的原理如图4所示。图中，Kpss为 PSS 控制的增益；Tω，T1，T2为控制器时间常数；m为补偿控制器阶数；ΔUpss为PSS输出电压增量。

图4 PSS的传递函数框图Fig.4 Transfer function block diagram of PSS

PSS控制器通过对频率偏差的校正，为系统提供一个正的阻尼转矩，在不影响输送容量的情况下提升了发电系统的稳定性。借鉴PSS的工作原理，通过改造原有VSG控制系统的电压环路，引入信号频率偏差，实现附加阻尼控制。电压控制环路的控制结构如图5所示。

根据图5可知，电压由3部分构成，分别为PSS控制（本文中补偿控制器阶数为0，即m=0）、无功调节及电压调节，VSG电压方程为

图5 附加阻尼控制结构图Fig.5 Structure diagram of additional damping control

式中：KQ，DU分别为无功和电压比例系数；Ug为电网电压幅值。

为了分析附加阻尼控制对系统动态特性的影响，建立含电压控制的VSG系统小信号模型。对文献[4]中电磁转矩、输出功率在稳态工作点附近进行线性化，在不考虑电网电压变化时可得：

式中：E0，U0分别为端电压和输出电压稳态值；K1～K5均为与系统稳态运行工作点有关的常数；Δδ为功角增量；ΔE为端电压增量。

对式（7）做拉普拉斯变换，并消去ΔE可以得到下式：

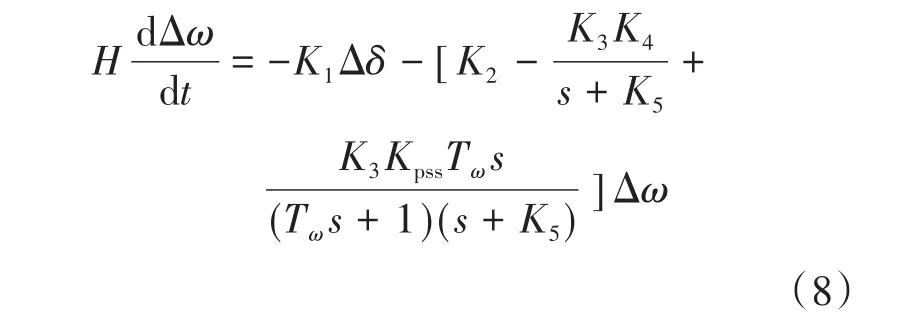
根据式（7）可以得到反应系统动态特性的传递函数框图，如图6所示。

图6 VSG附加阻尼系统的传递函数框图Fig.6 Transfer function block diagram of VSG additional damping system

从图6中可以看出，VSG系统的等效阻尼特性由3部分构成，分别为VSG下垂特性、电压耦合以及附加阻尼作用。其中，原有电压控制会产生一个负阻尼，削弱了VSG系统的阻尼能力。通过频率偏差信号的反馈，一方面可以抵消原有电压控制产生的负阻尼作用，另一方面也可以为系统提供额外的正阻尼，提高系统的阻尼能力，有助于提升系统的频率稳定。

根据式（8）可以得到在附加阻尼控制作用下系统的等效阻尼为

为了保障系统有足够的阻尼作用，需要对附加阻尼控制器进行设计。由式（9）可知，系统等效阻尼为复数量，为了提高对振荡的阻尼作用，要保障等效阻尼具有足够大的实部，从而产生足够的阻尼转矩作用，即Re[D（jωs）]＞n，ωs为振荡频率，n为系统所需最小阻尼系数[18]。

3 仿真分析

为了验证本文所提控制策略的有效性和正确性，利用Matlab/Simulink仿真平台搭建系统模型进行分析验证，系统的整体结构图如图7所示，图中两台VSG的容量比为2∶1，主要参数如表1～表3所示。

表1 VSG1主要参数Tab.1 The main parameters of the VSG1

表2 VSG2主要参数Tab.2 The main parameters of the VSG2

表3 负荷及线路阻抗参数Tab.3 The parameters of the load

图7 系统的整体结构图Fig.7 The overall structure of the system

3.1 VSG的惯量特性验证

为了分析VSG的惯量特性，图8a和图8b分别为离网、并网模式下，当受到负荷扰动时不同惯量系数下的频率输出特性。起始时刻VSG机组单独带负载运行，0.5 s时突加8 kW的有功负荷。并网运行时扰动与离网时相同。为了说明并网时大惯量对系统的影响，图9给出了并网模式下VSG的输出电流曲线图，图中可以明显看到大惯量作用下，并网电流受到扰动后存在明显的振荡过度过程。

图8 不同模式下VSG的频率特性Fig.8 Frequency characteristics of VSG in different modes

图9 并网模式下VSG的输出电流曲线Fig.9 Output current curve of VSG in grid-connected mode

由图8可以看出，VSG在离网和并网模式下不同惯量所表现的频率特性并不相同。具体表现为：离网时，较大的惯量可以缓解系统受到扰动的情况下频率变化率过大的问题，提高系统应对随机负荷的扰动能力；并网时，较大的惯量特性可能会使系统的振荡时间过长，在受到大的扰动时，持续的频率振荡可能触发频率保护动作，不利于系统的安全稳定运行。因此惯量的大小要视具体运行工况来设计，一味地追求大惯量也不一定有利于系统的稳定。

3.2 VSG的附加阻尼特性验证

为了分析VSG附加阻尼控制的有效性，对两台VSG并联运行时的动态特性进行验证。起始时刻两台VSG并联带载运行，输出功率为30 kW，分别由两台机组承担，3 s时突增8 kW的有功负荷，系统频率下跌；5 s时，第二台VSG增加8 kW的有功出力，频率恢复至额定值。图10为两台VSG在没有附加阻尼控制下的运行特性曲线。图11为VSG在附加阻尼控制下的输出特性曲线。

图10 两机并联系统输出特性曲线Fig.10 Output characteristic curves of two-machine parallel system

图11 附加阻尼控制下系统输出特性曲线Fig.11 System output characteristic curves under additional damping control

从图10可以看出，两机并联运行下，当受到负荷扰动时，系统由于阻尼能力不足导致系统发散失稳，频率和功率不能维持正常运行。由此可以看出，为了提高系统的稳定运行能力，增加系统的等效阻尼是非常有必要的。

对比图10、图11可以看出，在附加阻尼控制器的作用下，系统的稳定运行能力有所提高，在受到扰动时仍能够保持系统的稳定运行。这与前文分析的结论一致，附加阻尼控制可以有效地提升系统的阻尼能力，提高系统的稳定性。

为了直观地对比附加阻尼控制的优势，从阻尼、惯量及稳定性角度对比了附加阻尼控制与原控制的优势，具体对比如表4所示。

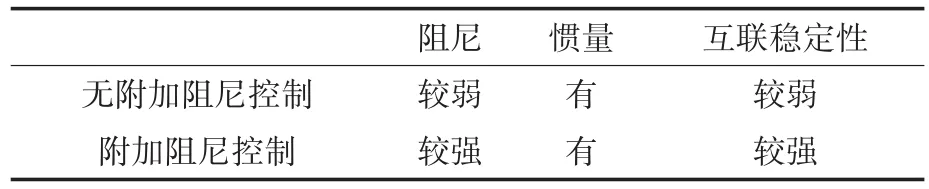
表4 附加阻尼控制性能对比Tab.4 The parameters of the load

从表4可以看出，在VSG中引入附加阻尼控制后，可以有效地改善系统的阻尼水平，同时不影响系统的惯量特性，互联系统的稳定性能够得到有效的提高。

4 结论

本文针对VSG系统动态特性弱的问题，提出一种附加阻尼控制策略，不需要改进电路结构及附加装备的条件下，通过对频率偏差信号的反馈即可实现VSG的附加阻尼控制。通过分析可以得到以下结论：

1）VSG的频率-有功与电压-无功控制的相互耦合弱化了系统的阻尼水平，尤其在VSG并联组网运行时阻尼能力会受到更大的影响，威胁系统的稳定运行；

2）借鉴电力系统PSS的原理，提出了附加阻尼控制，一方面可以抵消电压耦合带来的负阻尼，另一方面，通过参数的合理设计可以有效地提高系统的阻尼能力，提升系统的稳定性；

3）设计附加阻尼控制器时，只需要保证系统总的等效阻尼具有较大的实部，不需要完全补偿掉电压耦合带来的阻尼相位角。

本文对VSG的动态特性进行了分析，提出了一种附加阻尼控制，提高了VSG系统的稳定运行能力，但相关控制参数的优化设计没有进行充分的研究。后续工作将围绕附加阻尼控制器的参数优化设计展开。