基于改进动态下垂控制微网控制方法研究
常潇,侯哲晖,刘翼肇,李慧蓬,高乐 ,任学武
(1.国网山西省电力公司电力科学研究院,山西 太原 030001;2.国网山西省电力公司,山西 太原 030021;3.北京谦润和科技有限公司,北京 100193)
近年来,随着化石能源的持续高消耗,能源的可持续性成为了一个重要问题[1]。随着科技的进步,新能源以及可再生能源受到越来越多的关注。微电网是此分布式电源的主要载体,其运行时对环境的影响较小,还能有效缓解能源紧张问题[2-3]。利用逆变器作为微电网和大电网之间连接的桥梁,进而实现能量的传递[4-5]。因此,对逆变器的控制方法进行研究对系统稳定运行有重要意义。
为了能够有效抑制在运行模型变化过程对电网产生较大影响,需控制侧保持一致性,目前使用最普遍的为传统下垂控制方法[6-7]。然而传统下垂控制方法仍存在输出功率无法均分,甚至会造成较大的环流现象。由于其参数为固定设置,无法针对负荷变化时展开相应变化,将会造成输出不稳定[8-9]。因此,一些针对下垂控制方法的改进方法被研究。文献[10]将逆变器的基波以及谐波结合下垂控制能够降低电压谐波的影响,并根据容量较为合理地分配功率,增大功率均分精确度。文献[11]将负荷的电压幅值结合下垂控制,进而能够有效控制电压幅值,然而其造成无功功率的下垂系数大,影响系统的稳定运行。文献[12]在传统控制技术中引进虚拟电抗,进而让其输出阻抗为感性,并修正无功功率与电压幅值关系,最终实现无功功率均分的准确度,然而虚拟阻抗造成系统电压减小,影响输出电能质量。此外,还有一些基于鲁棒性或基于电网功率裕度等对下垂控制方法进行的改进[13-16],然而目前的改进方法仍存在系统的功率分配准确度不足、系统负荷发生突变时稳定性不足以及在逆变器并联运行时会引发环流等问题[17-18],因此亟待研究一种合理可靠的微电网控制方法。
为了有效抑制负荷波动对系统输出的影响,以及提高分布式电源并联运行时功率分配准确度,本文针对基于改进动态下垂控制的微电网控制方法展开了一系列研究。首先分析了传统下垂控制特性,通过引入动态下垂系数、灵敏度系数建立改进动态下垂系数控制模型,并通过仿真与实验对该改进方法与传统下垂控制方法结果进行对比,从而对该方法的可行性进行验证,其结果具有一定的工程实际意义。
1 下垂控制基本策略分析
下垂控制是微源的控制方法,主要能够完成逆变器有功功率以及无功功率的解耦控制[19]。因为在微电网里的输电线路距离比较短,且逆变器的输出阻抗主要是感性的,分别对其电压幅值以及频率进行调整,进而完成对无功功率以及有功功率的输出。
下垂控制通常针对多个逆变器并联运行时进行控制,系统中有两个逆变器并联运行时逆变器能够视为电压源,其等效电路如图1所示。

图1 逆变器并联运行等效图Fig.1 Parallel operation equivalent diagram of two inverters
传统的下垂控制效率受线路阻抗影响大,令阻抗与电感的比值不大时,微电网的有功功率输出和频率存在正比例关系,无功功率输出和电压幅值也存在正比例关系,其传统下垂控制表达式定义为
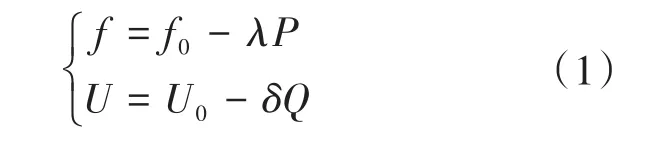
式中:f,f0分别为逆变器电压频率的实际值和基准值;U,U0分别为逆变器电压幅值的实际值和基准值;λ,δ分别为有功功率和无功功率的下垂系数;P,Q分别为系统的有功功率和无功功率。
该系统有功功率的下垂特性如图2所示,其中,两条曲线分别表示了两台逆变器特性。
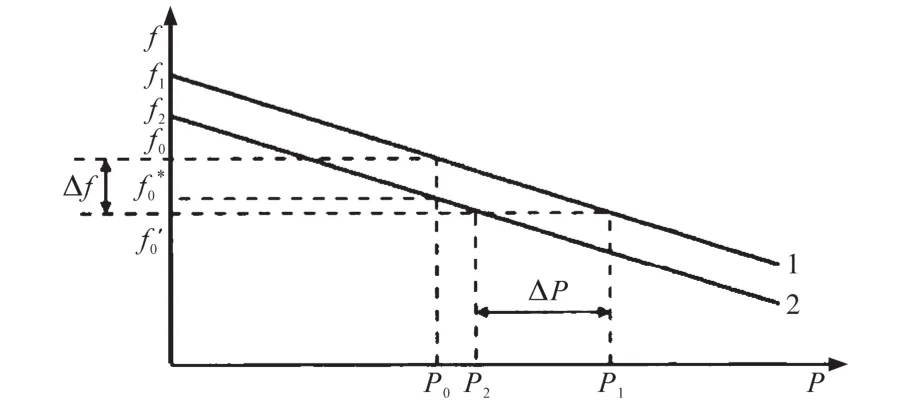
图2 有功功率的下垂特性Fig.2 Droop characteristic diagram of active power
通过图2中能够获得频率的变化关系为
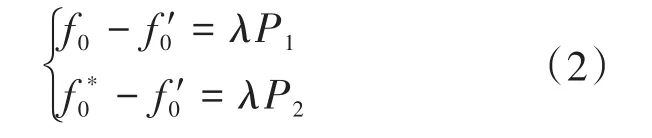
式中:f0*为逆变器的输出电压频率参考值;f'0为因负荷改变导致下降后的频率;P1,P2分别为两台逆变器在频率为f'0时的有功功率值。
进而能够得出有功功率下垂系数表达式为
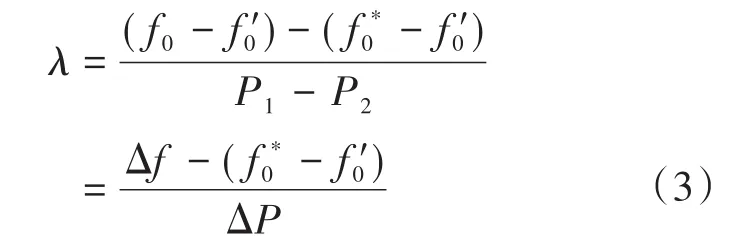
从式(3)中能够得到,当下垂系数λ增大时,其有功功率在一样负荷下的差值ΔP将会下降,频率差值Δf则会上升。因此,该λ值与ΔP以及Δf分别呈现正相关以及负相关的关系。而且无功功率的下垂系数与无功功率、电压幅值之间也存在该规律。
2 改进动态下垂系数的控制方法
2.1 动态下垂控制基本原理分析
在微电网系统里并联多个分布式电源发电,且都利用有功功率与频率的下垂控制策略时,因为不同的分布式电源的输出阻抗以及负荷情况都不一致,可能会导致不同的分布式电源的输出有功功率也有所不同,该差值容易造成环流现象。通过加入虚拟的阻抗,进而对其下垂系统进行调整,从而可以有效减小不同分布式电源间存在的有功功率偏差,然而该虚拟阻抗将会让系统对电压控制的有效性降低。因此,为有效降低有功功率偏差,同时保证系统控制的准确性,提出了一种改进动态下垂系数的控制策略。该策略把传统下垂控制方法里的固定下垂系数变换成具有功率变化和功率灵敏度系数的动态下垂系数,进而增大控制的准确性和有效性。其具体表达式为

式中:m1,m2为有功功率调节时的动态下垂系数;n1,n2为无功功率调节时的动态下垂系数;ε1,ε2为下垂控制系统中的灵敏度系数。
将式(1)和式(4)进行对比能够得到:利用有功功率的动态下垂系数m1+m2P替代原来的系数λ可以让下垂系数跟着功率的改变展开调整,进而有效保持(m1+m2P)P结果稳定,其下垂控制的系统结构如图3所示。灵敏度系数可以让系统在更短的时间内做出反应,进而对下垂系数进行调整,保障下垂控制系统的可靠性以及动态特性。

图3 下垂控制的系统结构Fig.3 System structure of droop control
2.2 动态下垂控制参数设计
改进的动态下垂控制的频率会随着有功功率的变化进行调整,动态下垂控制的频率与功率的关系如图4所示。在传统的下垂控制里有功负荷和系统频率呈现出反比例函数关系,并且其下垂系数即为恒定的斜率,因此传统的下垂控制是图4a中的m2值为0的直线。若有功功率达到目标值时,系统的频率将会逐渐趋于稳定,进而能够让电压在某区间内保持稳定,加强系统出现负载突变后的可靠性和稳定性。此外,通过设计下垂系数的灵敏度系数能够降低功率突变产生的超调量,进而能够保障系统的动态特征。

图4 动态下垂控制的频率与功率关系图Fig.4 The relationship between frequency and power of dynamic droop control
分布式电源并网运行的功率传递等效电路如图5所示。

图5 分布式电源并网等效电路Fig.5 Grid connected equivalent circuit of distributed generation
图5中,Z为输出阻抗;U,i分别为逆变器输出电压和电流;E为耦合点的电压;S为视在功率。通过该模型能够得出系统的P和Q的表达式为
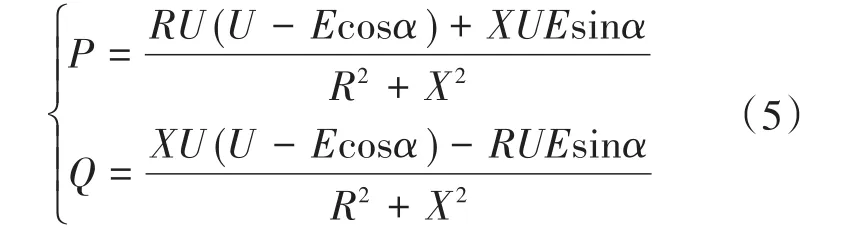
式中:R,X分别为系统线路电阻和电抗值;α为相角。
若逆变器的阻抗为感性,则式(5)能够变换为

为了有效降低谐波的不良反应,把有功功率以及无功功率通过低通滤波,进而得到小信号模型方程为
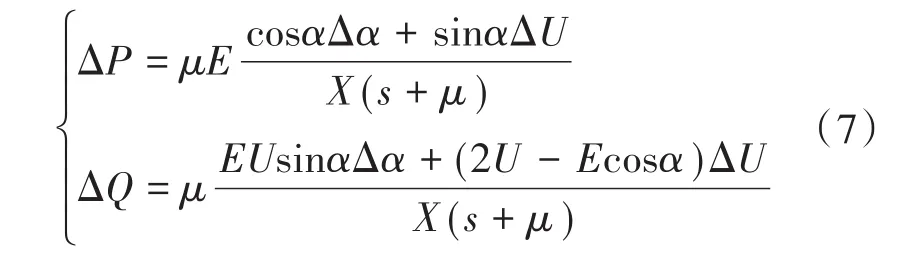
式中:μ为低通滤波的截断频率;Δα,ΔU分别为相角和电压幅值的波动。
令有功功率调节时的动态下垂系数m1和m2分别为

式中:fmax,fmin为频率的最大值和最小值;Pmax为最大的有功功率。
将式(4)和式(7)相结合得到根轨迹模型:

再结合图4将传统的下垂控制中下垂系数m1和m2分别设置为0.002和0,灵敏度系数ε1设置为0.03;改进动态下垂控制中下垂系数m1和m2分别设置为0.002和2.4×10-8。进而得到传统的下垂控制和改进下垂控制的极点曲线,如图6所示。
从图6a和图6b中能够得到,改进的动态下垂控制策略计算的极点与负实轴的距离较传统策略的短,改进后距离仅为传统的1/3,该值越小则系统的稳定性能越佳。从图6b和图6c中能够得到,通过加入灵敏度系数后,极点到不稳定区域的距离变大了,增大了20%左右,该距离越大,表明系统的动态调节特性越好。因此,加入灵敏度系数的改进动态下垂控制的动态调节特性较好。

图6 下垂控制的极点关系图Fig.6 Pole diagram of droop control
3 改进动态下垂控制仿真模型
为了对该改进动态下垂系数控制策略的稳定性和可靠性进行验证,搭建Simulink仿真模型,其微电网等效结构如图7所示。其中主要由3台分布式电源参与,并且将大电网等效为理想的三相电压源,PCC则表示并网开关。

图7 微电网等效结构Fig.7 Equivalent structure of micro-grid
改进动态下垂系数控制的仿真模型如图8所示,该模型由3台分布式电源参与,为了有效控制3个分布式电源之间不会产生环流,则须将其空载的频率和电压设置成一样。主要参数设定为:额定电压220 V,额定电压频率50 Hz,低通滤波电感和电容分别为3 mH和15μF,初始的有功功率和无功功率分别为4 kW和300 var。在仿真过程中,系统运行0.15 s后突加有功功率为1 kW、无功功率为100 var的负载;在0.35 s后再施加有功功率为1 kW、无功功率为100 var的负载;在0.55 s时脱离1 kW负载。
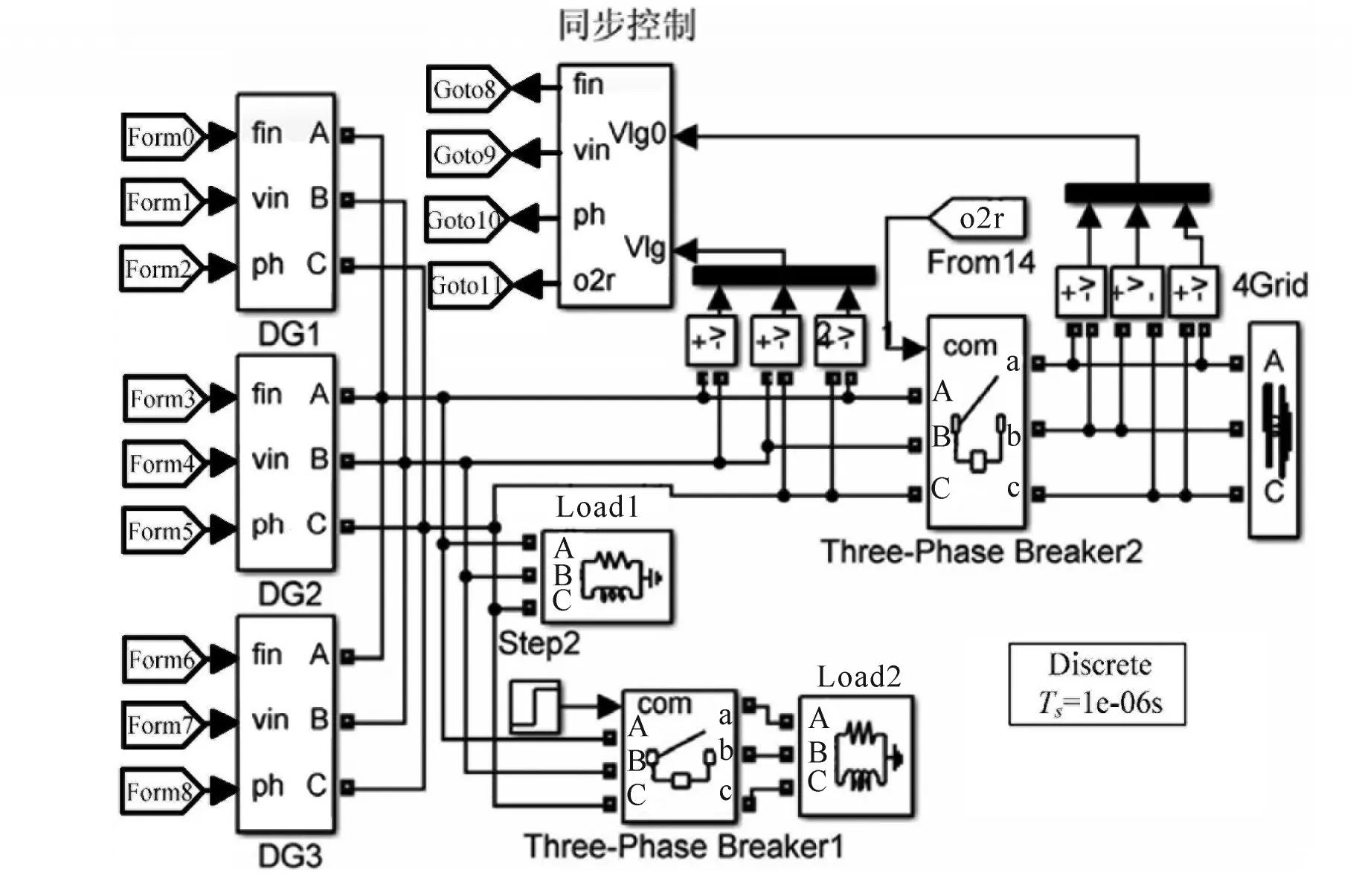
图8 改进动态下垂系数控制仿真模型Fig.8 Improved dynamic droop coefficient control simulation model
4 仿真结果与分析
在传统下垂控制和改进动态下垂系数控制下3台分布式电源输出的电压频率结果如图9所示,输出有功功率结果如图10所示。从图9中能够得到,在传统下垂控制下,系统几次投切负载时,3台分布式电源的频率均从50 Hz降低至49.75 Hz,表明电压频率受系统投切负载时影响较大;而改进动态下垂系数控制下,在突加和脱离负载时频率波动都较小,仅仅降低0.003 Hz,基本仍保持在50 Hz,表明该方法下系统电压频率稳定性和准确性高。结合图10能够得到,两种方法对输出有功功率的精度接近,且均较为准确。因此,所提的改进控制方法具有较高精度,能够有效投切负荷,并减小波动,大幅度提高了系统的稳定性。
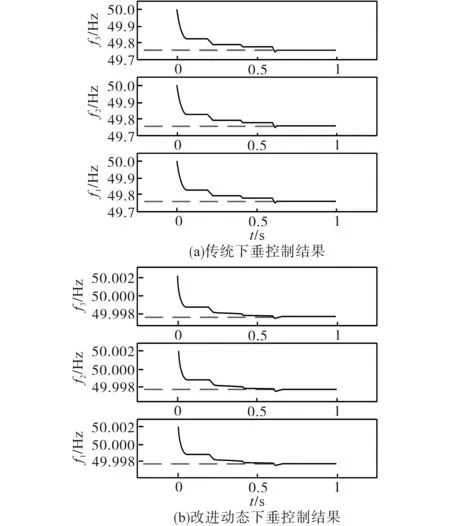
图9 输出电压频率对比结果Fig.9 Output voltage frequency comparison results

图10 输出有功功率对比结果Fig.10 Output active power comparison results
在传统下垂控制和改进动态下垂系数控制下,输出电压幅值结果和输出无功功率分别如图11和图12所示。从图11中能够得到,传统下垂控制在负载投切时,其电压幅值从312.2 mV跌落至311.4 mV,而改进的下垂控制系统中电压幅值则从311.4 mV跌落至311.15 mV,更为接近输入电压,因此表明在改进动态下垂系数控制下电压随着系统负荷投切的变化明显降低。从图12中能够得到,在传统下垂控制下其输出无功功率最终稳定在260 var,而在改进动态下垂系数控制下,其输出无功功率最终稳定在400 var,进一步表明了基于改进动态下垂系数控制方法更加准确和有效,大大提高了系统的稳定性和电能质量。
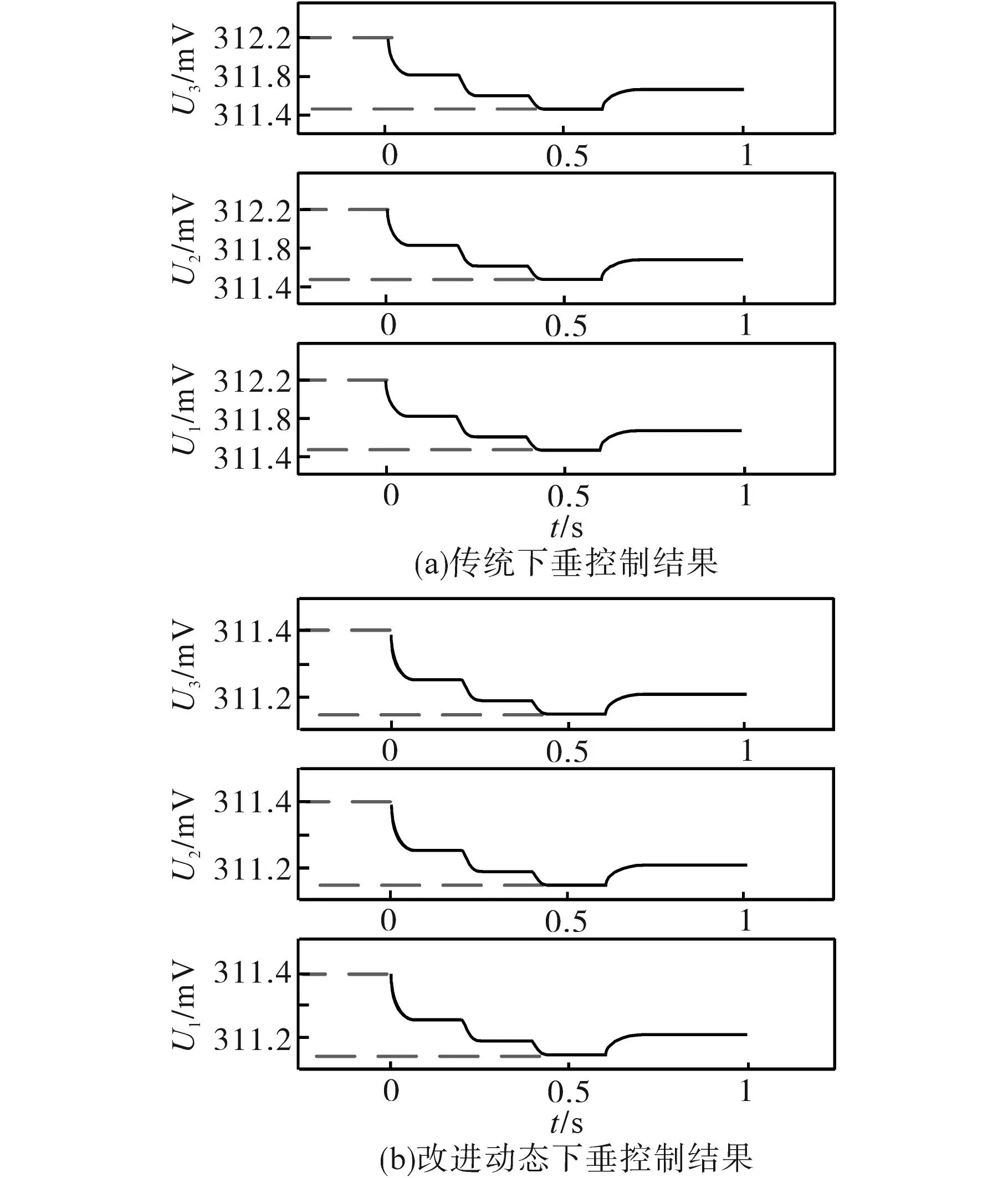
图11 输出电压幅值对比结果Fig.11 Output voltage amplitude comparison results

图12 输出无功功率对比结果Fig.12 Output reactive power comparison results
5 实验结果验证
为了进一步验证所提改进动态下垂系数控制方法的可靠性,搭建实验平台,利用3台3 kW的逆变器样机展开实验,负载谐振角频率设定为20 rad/s,设置线路阻抗为(0.2+j0.58)Ω,等效结构见图7,实验平台如图13所示,通过负载箱可实现负载的变化与调节,综合单元能够实现模拟线路阻抗。

图13 实验系统平台Fig.13 Experimental system platform
实验系统输出的有功功率以及电压频率结果如图14所示。从图中看出,在施加负荷的情况下,传统下垂控制方法频率降幅达到了0.24 Hz,而所提的改进动态下垂系数控制方法其频率降幅仅为0.05 Hz,两种方法的有功功率一致,进而表明所提改进动态下垂系数控制方法得到的结果更为稳定,频率下降幅度更小。
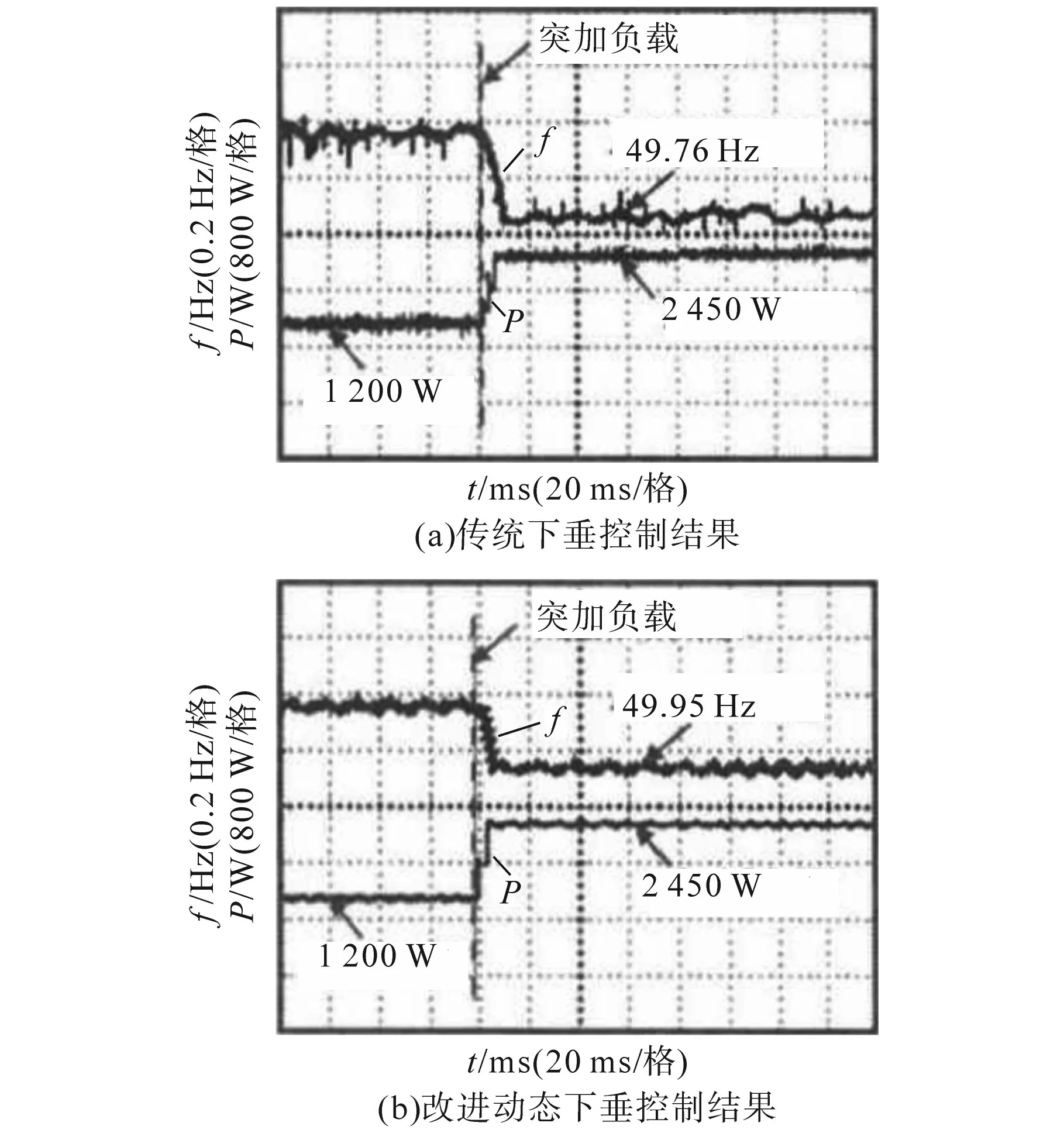
图14 有功功率和电压频率实验结果Fig.14 Active power and voltage frequency test results
系统输出的无功功率以及电压幅值结果如图15所示。从图中能够看出,在施加负荷的情况下,传统下垂控制方法的电压幅值降幅ΔU1达到了100 V;而所提的改进动态下垂系数控制方法其电压幅值降幅ΔU2仅为30 V,有效抑制了电压的下降,同时有效减小了系统的环流,动态响应速度更迅速,进而进一步验证了所提改进动态下垂系数控制方法的有效性和可靠性。
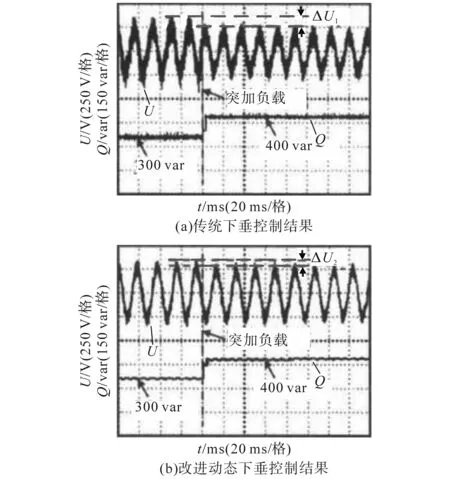
图15 无功功率和电压幅值实验结果Fig.15 Reactive power and voltage amplitude test results
6 结论
本文研究了基于改进动态下垂系数控制策略,以克服多个分布式电源并联运行时造成的控制准确性不足等问题。对所提控制方法进行仿真与实验得到:基于改进动态下垂系数控制方法能够有效抑制在电网投切负荷时出现的电压下降以及系统输出功率的变化,该方法利用灵敏度系数有效提高动态特性,保障功率均分作用以及稳定性。在仿真模拟中负载突变时,基于改进动态下垂系数的微电网控制下电压频率仍保持在50 Hz水平,而传统下垂控制其频率下降达到0.3 Hz,对有功功率与无功功率的输出控制也更为准确。实验模拟突加负载情况时,基于改进动态下垂系数控制策略对系统的电压、频率等控制更为准确和稳定。因此,仿真和实验结果验证了基于改进动态下垂系数控制策略不仅能够保障良好的动态特性与功率均分效果,还能够显著提高电能质量。其结果对微电网控制方法具有重要的参考意义,进一步推动了微电网控制技术的发展。

