人体生理参数参考区间的制定方法和应用

何慧婧，单广良

(中国医学科学院基础医学研究所 北京协和医学院基础学院 流行病学与卫生统计学系, 北京 100005)

生理参数及其标准存在人种、民族和地区间的差异[1-2]。制定符合不同人群生长发育规律的生理参数值范围，可使疾病筛查和临床实践更有针对性[4]。

生理参数参考区间(reference interval, RI)的计算有严格的方法学和规范化要求，美国临床实验室标准化协会(clinical and laboratory standards institute, CLSI)第3版RI制定指南(C28A3)[3]系统介绍了RI的计算方法及其应用，然而国内目前尚无相关方法学介绍。因此，本文旨在系统介绍生理参数RI的制定方法及其应用时的注意事项。

1 制定生理参数值参考区间的流程

1.1 明确研究目的和目标人群

针对不同人群特点和指标类型，RI的计算需要考虑的因素略有不同。例如儿童临床指标RI的制定，需要考虑按年龄等影响因素进行亚组划分[4]；而老年人也可能在某些生理指标方面与一般人群存在差异，RI因此也会不同[5]。一些在民族或种族间存在差异的生理指标，在制定RI时也须明确目标人群来源[6-7]。

1.2 确定参考人群

明确目标人群后，还需明确参考人群(reference individual)。如制定中国健康成人血压值的RI，首先要定义“健康”。然而，绝对的健康是难以界定的，在实际应用中往往根据研究目的而制定健康的相对标准[4, 8-9]，即参考人群中不存在影响血压值的病理因素。根据研究目的不同，可以有不同的纳入和排除标准。

C28A3中列举了一些常见的需要排除的人群(因研究而异，表1)。另外，还可通过文献查阅、专家咨询等方式，确定影响某个或某类指标的影响因素，制定出具体的研究对象纳入和排除标准。现场调查时，可通过问卷调查、体格测量、实验室检测等获得人群健康相关信息，从而按照纳入排除标准限定参考人群。

1.3 异常值的识别和处理

1.3.1 异常值(outlier)的识别:排除可能影响生理参数值的因素后，还需要识别和处理异常值。研究者可首先把分析指标的分布情况以图形方式展示(散点图、箱式图、概率密度图等)，大致了解数据分布特点[3]。识别异常值的方法主要有参数法和非参数法两类。

1) 非参数法，其中有代表性的为Dixon-Reed法则。主要思路是：一组数据按大小排序后，如果极值(最大值或最小值)与其相邻数值的差值(differ-ence, D)大于该组数据(包括该极值)极差(range, R)的1/3，则判断为异常值，即D/R>1/3。虽然Dixon-Reed法易于理解，但实际应用时存在一定的局限性：当数据一端存在多个异常值时，该法则存在“掩盖性”(masking)[3, 9]。非参数法判断异常值的优势为不依赖数据分布特点，易于理解，有较广泛的适用性。

2) 参数法，其中有代表性的Tukey法则。与Dixon-Reed法不同，该方法要求数据满足正态分布，因此是一种参数估计法。对于不满足正态分布的数据，首先要进行数据转换。数据转换可以应用Box-Cox转换[10]。将非正态分布数据转换为正态分布后，计算该组数据的四分位数间距(interquartile range, IQR)和第25、75百分位数值(Q1，Q3)，应用以下公式确定数据的上下限界值：

上限：Q3+1.5×IQR；下限：Q1-1.5×IQR

Tukey法的优点是不存在Dixon-Reed法则的异常值掩盖问题，但缺点是可能将一些本不属于异常值的数据误删，进而导致RI范围变窄；此外，如果数据变换后仍不满足正态分布，使用Tukey法删除异常值，可能会使参考区间的估计存在偏差。

1.3.2 异常值的处理:按照以上两种方法识别出异常值后，是否将其删除尚存在争议。C28A3认为，除非有证据表明异常值为错误记录，否则不宜将其删除。事实上，在应用非参数法估计参考区间时，是否删除异常值对结果几乎没有影响。不过也有学者建议，无论应用非参数法或稳健估计法计算参考值区间，都应删除异常值，以获得更准确的区间估计[9]。无论Tukey法或Dixon-Reed法在识别异常值方面均存在一定的局限性，对异常值的取舍要结合研究目的与样本数据特点谨慎选择。

表1 可能需要考虑的参考人群排除因素(视具体研究目的而定)[3]

1.4 参考区间的计算方法

确定样本人群后可计算RI。RI是由下限和上限所限定的一个范围，通常为95%，表示样本人群95%的指标值落在该范围内。RI的计算方法主要包括参数法、非参数法和稳健估计(robust estimation)法3类。

1.4.1 非参数法:该方法基于数据的百分位数分布来确定参考值范围。例如，拟计算某指标95%的RI，下限即第2.5百分位数(P2.5)，上限即第97.5百分位数(P97.5)。非参数法思路容易理解，易于操作，且对数据分布类型没有要求，适用性广，因此也是C28A3推荐使用的RI估计方法。中国健康汉族成人全血细胞数值RI估计即采用非参数法[11]。

1.4.2 参数法:该方法要求数据符合正态分布，不满足正态分布时需首先进行数据转换。应用转换后的数据，基于正态分布的曲线下面积进行RI估计。数据转换方法可采用Box-Cox转换。应用Box-Cox转换得到y值后，再将其进行标准化转换，将数据分布转换为标准正态分布，即：z=sign(y)·|y|K，其中K为常数。将变换的数值z进行正态性检验，符合正态分布后应用以下公式计算RI：

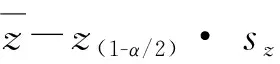
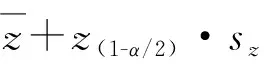
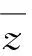
1.4.3 稳健估计:适用于小样本数据的RI估计，可以视为一种介于参数与非参数估计之间的方法[3]。无论是参数法还是非参数法，按照国际临床检验联盟的建议，都要求计算RI的样本数据不少于120[12]。然而某些人群很难达到参数区间估计的最小样本量要求，如新生儿等特殊人群，应用传统估计方法可能会使RI估计产生较大偏差。此时可采用稳健估计[13]。该方法可适用于仅有20～40个样本的RI估计。

1.4.4 不同RI计算方法的比较:对于样本量较大的数据，应用3种方法估计RI结果相差不大(见表2)。对于小样本数据，更适合使用稳健估计。此外，无论使用哪种估计方法，应用样本统计量推断总体参数，都需要计算RI上下限的可信区间，以对估计的精度进行评估。

综上所述，制定生理参数RI的流程与方法可概括为图1。

2 生理参数参考区间制定的应用与注意事项

生理参数RI估计对于健康评估、疾病筛查与诊断、治疗效果评估等具有重要意义。本文为国内学者估计生理参数RI提供了方法学依据和参考。除了方法学之外，还需要注意以下方面。

首先，信息收集的真实性与准确性。数据信息的真实性和准确性、生物样品的规范采集和存储是保证RI准确估计的前提，因此必须依据现场调查和相关实验室指南进行规范化操作。此外，不同实验室和实验仪器分析结果也可能存在差异，需进行结果比较和偏倚估计[14]。

表2 非参数法、参数法和稳健估计法计算参考区间(RI)的方法学比较Table 2 Comparison of non-parametric, parametric, and robust methods in reference interval(RI) estimation

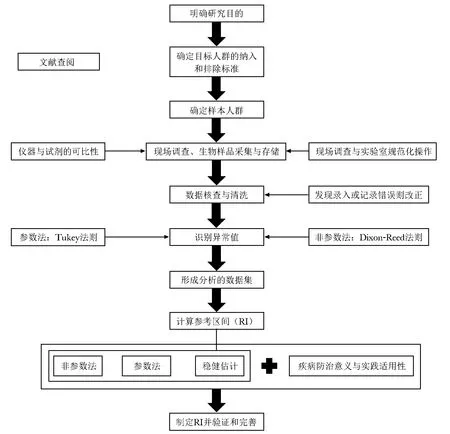
图1 制定生理指标值参考区间(RI)的流程Fig 1 Flow chart of reference interval(RI) estimation

其次，参考区间估计的适用性。生理参数RI估计，不仅要考虑统计学方法，还要考虑在临床或疾病筛查时的适用性以及卫生经济学效益。因此，人体生理参数参考区间的制定，应是综合科学性、可行性、适用性的应用研究。

3 结语

生理参数参考区间的制定对于完善本土化的疾病筛查与诊断有重要意义。本文通过对国内外参考区间方法学的回顾，系统梳理了RI制定的方法和流程，可为中国学者完善生理参数参考区间的制定和应用提供有价值的参考。

志谢：中国医学科学院基础医学研究所韩伟老师为本文提供了方法学支持，特此感谢。