有限信息约束下的离散鲁棒滤波器设计

凌荣耀，冯 宇

1(浙江工业大学 信息工程学院，杭州 310023)2(大西洋高等矿业电信学院 自动化系，法国 南特 44300)

1 引 言

滤波器能从含有干扰的测量信号中估计出未知的系统状态信息，是一类用于抑制干扰的重要工程应用元件，被广泛应用于电力电子、航天技术、工业控制、医疗器械等众多领域[1-5].自被提出以来，卡尔曼滤波器已经被广泛应用于各类工程实践[6].该滤波方法高度依赖于精确的滤波对象模型以及外部扰动的概率分布特征.当外部扰动或滤波对象参数的先验信息未知的情况下，H∞滤波是一种可选的替代方案[7].

随着计算机和网络通信技术的发展，通信网络在工程实践中得到越来越多的应用[8，9].同时，网络环境具有一定的随机性，其中存在的量化[10]、时延[11-13]、丢包[11，14]、网络入侵[15]等现象都可能对系统的实际性能产生影响.针对上述因素，基于通信网络的滤波器设计问题也得到了众多研究的关注.文献[14]引入马尔科夫链用以描述信道的丢包现象，并讨论了数据包丢失过程与卡尔曼滤波器的稳定性之间的关系.针对动态标签跃迁产生的延迟问题，文献[16]提出一种基于卡尔曼滤波的数据清洗方法.文献[17]提出了一类具有对数特性量化级的量化器，使得数据在量化后具有统一的相对误差界，文献[10]在此基础上给出了分段函数的表达方式，现实了对此类量化器的描述.文献[18]研究了基于量化测量信息的模糊系统的滤波器设计问题.文献[19]研究了基于量化测量信息的传感器网络的分布式滤波问题.

针对对数量化器的现有研究通常假设各量化器的量化噪声相互独立并将量化噪声描述为有界的系统参数不确定性加以处理[10，17].本文将量化噪声建模为独立于量化输入的随机噪声，采用随机系统的方法实现滤波误差系统的建模，将滤波误差系统建模成一个具有多个随机变量的不确定性系统.进而基于随机系统分析方法，通过黎卡提方程给出了滤波误差系统均方稳定且符合给定H∞性能指标的条件，同时给出了对应H∞滤波器的设计方法.最后，通过仿真算例验证了本文所提设计方法的有效性.本文中，上标“T”表示矩阵转置，I表示适当维数的单位矩阵，Tr{A}表示矩阵A的迹，E{·}表示数学期望，‖·‖表示欧几里得范数，运算符⊙代表哈达玛积.

2 问题描述

考虑如图1所示的滤波系统，其中，滤波对象由如下离散线性时不变系统描述：

(1)

其中，x(k)∈n，y(k)∈p分别为滤波对象的状态向量和测量输出.随机噪声w(k)∈m用于表示外部扰动输入或者系统的参数不确定性.z(k)∈l是待估计的滤波对象的加权状态信息.A，B，C1，C2，D分别是适当维数的已知常数矩阵.式(1)中的信号z(k)通常无法精确采集，因此需要设计滤波器对其进行估计.假设式(1)中的矩阵对(A，C1)是能观的且测量输出y(k)中的各分量分别以单包的方式传输.

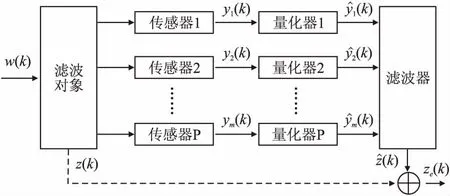
图1 滤波系统结构图Fig.1 Structure diagram of the filtering system

如图1所示，式(1)的测量输出y(k)通过量化器量化后发送至滤波器.各量化器采用文献[10]中提出的对数量化策略，对应的量化过程可由如下分段函数表示：

(2)

其中，v(k)∈是量化器的输入，参数0<ρ<1是量化器的量化密度，ui=ρiu0，i=1，2，3，…，是量化器的量化级，u0称为初始量化级，δ=(1-ρ)/(1+ρ)称为量化器的最大误差系数.易知，量化密度ρ越大，量化器的量化精度越高.根据式(2)，量化器输出Q[v(k)]可进一步表示为：

Q[v(k)]=v(k)+Δv(k)v(k)

在如图1所示的滤波问题中，各量化器均采用式(2)中所述对数量化策略且各量化器的量化密度分别为0<ρj<1，j=1，2，…，p.进而可得各量化器的输入输出关系如下：

其中，

Δj(k)∈[-δj，δj]，δj=(1-ρj)/(1+ρj)，E{Δj(k)}

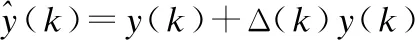
(3)

其中，

Δ(k)=[Δij(k)]，i，j=1，2，…p描述了各量化器之间的耦合关系.不同于现有方法，本文所述建模和设计方法可以处理各量化器的量化噪声存在耦合的情况.特别的，当量化噪声相互独立时，可得式(3)中：

E{Δ(k)}=0，E{Δ2(k)}=Λ，

Δ(k)=diag{Δ1(k)，Δ2(k)，…，Δp(k)}，

本文考虑如下结构的滤波器：

(4)

(5)

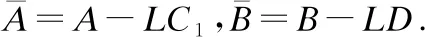
注意到滤波误差系统式(5)包含随机变量Δ(k)和随机噪声输入w(k)，为分析滤波误差系统式(5)的性能，首先给出如下定义.

定义1. 随机信号u(k)=[u1(k)，u2(k)，…，um(k)]∈m是能量有界的，若Ruu(τ)和Suu(ω)存在且满足：

其中，

定义2.记p表示所有能量有界信号的空间，则在空间p中定义如下范数：

定义3.对信号u(k)=[u1(k)，u2(k)，…，um(k)]∈m和v(k)=[v1(k)，v2(k)，…，vm(k)]∈m，定义其N点內积如下：

定义4.对于线性映射算子J：q→l，其伴随算子Ja定义为Ja：l→q，且对于任意X∈q和Y∈l有如下等式成立：

〈J{X}，Y〉=〈X，Ja{Y}〉

定义6.式(5)满足H∞性能指标γ，如果式(5)是均方稳定的，并且满足如下性能指标：

在所考虑的滤波问题中，假设式(5)中的随机噪声w(k)是能量有界的，即w(k)∈p.则本文所述的滤波问题可总结为如下问题.

问题.设计滤波器式(4)中的增益矩阵L，从而使得滤波误差式(5)是均方稳定的，并且满足H∞性能指标γ.

3 主要结果

针对第2章中提出的问题，本节将分析式(5)的均方稳定性以及H∞性能，进而给出滤波器式(4)中的增益矩阵L的设计方法.为便于后续讨论，首先针对式(5)定义线性映射算子T并进而给出与其相关的引理.

当k=0，由式(5)可得：

ze(k)=C2e(0)

(6)

当k>0由式(5)可得：

(7)

其中，

注意到式(6)和式(7)表示从w(k)和e(0)到e(k)的输入输出关系.从而可以定义对应的线性映射算子：

T：[w(k)，e(0)]→ze(k)

(8)

并定义T的伴随算子为：

Ta：ze(k)→[wa(k)，ea(0)]

(9)

对于式(8)及伴随式(9)，有如下引理所述的性质成立.

引理.当e(0)=0，ea(0)=0，对线性映射式(8)及其伴随式(9)有如下公式成立：

(10)

证明：基于定义4可知算子T和Ta满足下列公式：

〈T{[w(k)，e(0)]，ze(k)}〉=〈[w(k)，e(0)]，Ta{ze(k)}〉

(11)

其中，式(11)右侧可基于定义3改写为：

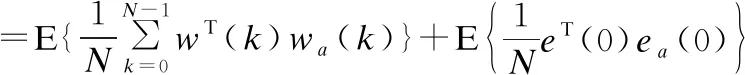
且式(11)左侧可改写为：

将式(7)中ze(k)的表达式代入式(11)可得：

为使式(11)成立，上式中的ea(0)和wa(k)可选取为：

从而可得算子Ta的状态空间表达式为：

(12)

其中，

为证明等式(10)，定义如下算子：

(ze(k)，[w(k)，e(0)])=〈ze(k)，T{[w(k)，e(0)]}〉

(13)

以及对应的范数：

(14)

注意到T{[w(k)，e(0)]}=ze(k)，式(14)可改写为：

当e(0)=0，可得：

(15)

另一方面，根据定义4，式(13)可改写为：

H(ze(k)，[w(k)，e(0)])=〈ze(k)，T{[w(k)，e(0)]}〉=〈Ta{ze(k)}，[w(k)，e(0)]〉

从而式(14)可对应改写为：

进而，由施瓦兹不等式可得：

当ea(0)=0，可得：

(16)

根据式(14)和式(15)可知：

即式(9)成立.

接下来的定理中将通过黎卡提方程给出求解第2章中所提问题的具体方法.

定理.给定常数γ>0，若存在矩阵P>0使如下黎卡提方程成立：

(17)

则滤波误差式(5)是均方稳定的，同时满足给定的H∞性能指标γ，并且对应的滤波器增益矩阵可由下式给出：

(18)

证明：首先证明误差系统式(5)的均方稳定性.式(5)是均方稳定的，当且仅当式(12)是均方稳定的.对式(12)选取如下Lyapunov函数：

(19)

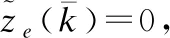
(20)

另一方面，式(17)和式(18)可分别改写为：

(21)

(22)

其中，

将式(22)代入式(21)可得：

从而可得下式成立：

(23)

进而可得：

因此可得：

即式(12)是均方稳定的，从而可以证明滤波误差式(5)的均方稳定性.

接下来，进一步分析滤波误差式(5)的H∞性能.由黎卡提方程式(17)和式(19)可得：

其中，

对上式移项可得

另一方面，由式(21)可得：

从而可得：

进而可得：

根据本章节中引理可知当外部噪声输入w0(k)≡0时，

即式(5)满足给定的H∞性能指标γ.

注释1. 注意到式(17)不是标准的黎卡提方程，难以直接求解其中的矩阵P.为此，本文给出如下迭代算法用于计算满足黎卡提方程式(17)的数值解P.

步骤4.设k=k+1，返回步骤2.

(24)

若式(24)中的优化问题有解，则滤波误差系统式(5)满足最优H∞性能指标γmin且对应的滤波器增益L可根据式(18)求得.

4 仿真算例

为验证本文所提设计方法的有效性，考虑式(1)中的各参数矩阵取值如下：

滤波对象的测量输出通过两个独立量化器进行量化，其量化密度分别为ρ1=0.9，ρ2=0.8.通过求解优化问题式(24)可得：

进而通过式(18)求得滤波器式(4)中增益矩阵L的值为：

在仿真中，取式(1)中扰动w(k)为：

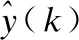
图2 量化误差Fig.2 Quantization errors 图3 滤波效果Fig.3 Filtering performance 图4 滤波误差Fig.4 Filtering errors

上述仿真结果验证了本文所提的滤波器设计方法有效.

5 总 结

本文研究了一类有限信息约束下的离散系统鲁棒滤波问题.文中同时考虑了数据量化和随机噪声的影响.采用随机系统的建模方法，最终将滤波误差系统建模成一个包含多个不确定性的随机系统.通过随机系统分析方法和黎卡提方程给出了滤波误差系统均方稳定且具有给定噪声抑制率的条件及对应滤波器的设计方法.最后通过仿真算例验证了所述方法的有效性.