基于块重构的加密域可逆信息隐藏

杨 阳，李欣然，胡锦川

上海理工大学光电信息与计算机工程学院，上海200093

可逆信息隐藏（reversible data hiding,RDH）是一种可以在提取嵌入的秘密数据后无损地恢复载体图像的技术。RDH 技术所具备的无损性以及可逆性，使其在医学图像、军事图像和法律取证等领域中得到广泛应用。一般来说，可逆信息隐藏可分为面向明文图像的可逆信息隐藏和面向密文图像的可逆信息隐藏[1]。

对于明文图像，从嵌入方法的角度来看，现有的RDH 方法可以分为3 类：基于无损压缩的方法[2-3]、基于差值扩展的方法[4-6]以及基于直方图平移的方法[7-10]。RDH 也吸引了众多研究者的关注，在文献[3]中数据隐藏端通过无损压缩的方式压缩载体图像，目的是对腾出空间进行数据嵌入。文献[6]通过扩展每个像素对的差值，使得对应差值的最低有效位（least significant bits,LSB）为零，以用于嵌入数据。文献[9]指出自然图像灰度值的直方图分布不均匀，因此可以通过修改直方图的方式嵌入秘密数据。这些RDH 方法基本上都是利用明文图像中的冗余，以可逆的方式嵌入秘密数据。若图像已被加密，那么类噪声的加密图像会丢失大量冗余空间。因此，这些方法均不适合用于在加密图像中嵌入数据。近年来，随着云存储和云计算的快速发展，大量的私有数据被存储在云服务器上，并进行一定处理。为了有效地保护这些隐私内容，用户的数据需要先进行加密，然后才能被传输到云服务器上，可见隐私保护已成为内容所有者关注的焦点[11-18]。在加密域中，内容所有者需要在不泄露载体图像内容的前提下借助于云服务器来实现信息隐藏。

下面就如何实现加密图像中的可逆信息隐藏（reversible data hiding in encrypted image,RDHEI）进行简单说明。在RDHEI 方法中，内容所有者先对原始图像进行加密，然后将加密后的图像发送给数据隐藏端。随后，数据隐藏端将其他数据（如用于恢复的标签数据和用于验证的哈希序列）嵌入到加密图像中。接收端可根据不同的需求实现数据提取、图像解密以及图像恢复。因此，RDHEI 方法的关键就是从加密图像中找到一个可用空间进行数据存储，同时确保数据提取和图像恢复的准确性。

现有的RDHEI 方法可分成两类：一类是加密后腾出空间（vacate room after encryption,VRAE）以嵌入数据[13,17-27]，另一类是加密前预留空间（reserve room before encryption,RRBE）以嵌入数据[16,28-33]。

文献[17]提出了一种基于VRAE 的RDHEI 方法，用户根据加密密钥通过按位异或的方式进行图像加密，然后将加密后的图像分块。通过在每个块中翻转一半像素的3LSBs，可以将消息嵌入到所腾出的空间中。根据解密图像的空间相关性，在一个块中找到翻转的部分，然后在接收端实现数据提取和图像恢复的可分离操作。但是，该方案的图像恢复依赖于图像的局部平滑性，因此所恢复的图像可能具有一定的误差。文献[22,34]提出了两种新的平滑函数来提高图像恢复的准确度，但这两种方案都无法准确地恢复图像。文献[23]提出了一种基于块的方法对原始图像进行加密，该方法保留了相邻像素之间的相关性，使得之前众多针对明文图像的RDH 方法都可以在加密域中得到运用。文献[27]提出了一种密文图像的无损、可逆和组合数据隐藏方案，加密方法是基于概率性和同态性的公钥加密系统实现的。

文献[28]基于RRBE，在加密之前采用传统的RDH 算法在原始图像中预留空间，以便于在加密域中可逆地嵌入数据。文献[30]提出了一种将消息位嵌入到二值图像中的二值块嵌入（binary-block embedding,BBE）方法，在提高嵌入率的同时增强了安全性；并且提出了一种可逆的加密域数据隐藏方案。在该方案中，内容所有者利用BBE 方法对原始图像的所有位平面进行压缩，并在加密前将LSB 压缩结果嵌入到最高有效位（most significant bits,MSB）中，通过这种方式实现在LSB 中为数据隐藏预留空间。文献[21]对二值图像中的块进行了重排，并利用获得的冗余和一定的像素预测方法来嵌入额外的数据，但是该方案在实现可观的嵌入率时是以一定程度的失真为代价的。文献[33]使用了扩展游程编码和基于块的MSB 平面重排方式在图像加密前腾出空间用于数据嵌入。

一般来说，比起基于VRAE 的RDHEI 方案，基于RRBE 的RDHEI 方案能实现更大的嵌入空间。并且，基于RRBE 的RDHEI 方案在图像加密前需要进行额外的预处理操作，这会增加内容所有者的计算负担。因此，基于VRAE 的RDHEI 方案比基于RRBE 的方案具有更广泛的适用性。

为了进一步提高信息隐藏的容量和图像恢复的准确性，本文提出了一种基于块重构的RDHEI 算法，该算法在一定程度上实现了信息嵌入率的提高和直接解密图像的解密质量的优化。在本文的方案中，内容所有者采用一种有效的加密方法对每个原始块进行加密，能有效地保护原始图像的内容，同时将冗余从MSB 转移到LSB。通过将LSB 平面的所有块划分为均匀块（全黑或全白像素组成）和非均匀块（黑白像素共同组成），达到将辅助数据和附加数据嵌入到所有腾出的空间的目的。文献[21]将分类方法应用于二值图像，像素预测方案在进行图像恢复时会造成一定程度的失真，而本文利用固定像素来改善上述情况，即利用加密密钥和数据隐藏密钥，在接收端实现了数据提取、图像解密和图像恢复的可分离操作。实验结果表明，本文所提方案在嵌入率、解密图像的视觉质量和图像恢复准确度等方面都有很好的表现。

1 基于块重构的加密域可逆信息隐藏算法

本节基于块重构的RDHEI 算法可分为3 个部分：图像加密、数据嵌入、数据提取和图像恢复。在图像拥有者端，使用特定的图像加密方法对原始图像进行加密，从而生成加密图像。在信息嵌入者端，额外的数据信息被嵌入到加密图像中。在接收者端，根据加密密钥和数据隐藏密钥的可用性，能够可分离地实现图像解密、信息提取和图像恢复。图1是本文提出的基于块重构的加密域可逆信息隐藏算法的流程框图，下面逐一介绍流程图中的各个模块。

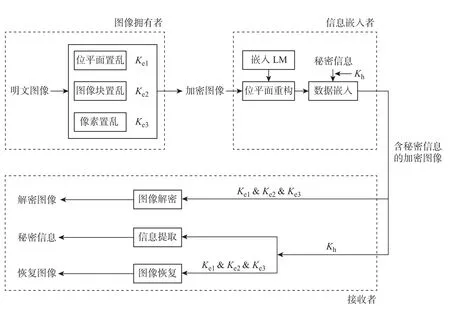
图1 基于块重构的加密域可逆信息隐藏流程框图Figure 1 Flowchart of RDH in encrypted domain based on block rearrangement

1.1 图像加密

记原始明文灰度图像为Io，大小为M ×N，Ii,j表示明文图像Io位于(i,j) 坐标的像素点的像素值，其中1 ≤i≤M，1 ≤j≤N；Ii,j的8 比特位记为bi,j,u(u=1,2,···,8)，且

在图像加密阶段中，图像拥有者首先将明文图像Io分成P个不重叠的图像块，每个块的大小为S×S，则块数P=MN/S2（为了简化计算，本文假定M和N都能被S整除）。接下来利用加密密钥Ke1对位平面进行置乱，其中，Ke1密钥由P个子密钥组成，与P个图像块形成一一对应的关系。根据每一个子密钥(r=1,2,···,P) 能够得到1～8 范围内的不重复整数，其中前λ个数字和后(8-λ) 个数字都是从集合{1,2,···,λ}以及{λ+1,λ+2,···,8}中得到的，从而原始像素的λ位MSB 就被随机移动到λ位LSB中，同时(8-λ) 位MSB 被随机移动到(8-λ) 位LSB 中。

下面通过一个例子具体说明加密过程：假设λ=4，某一个原始像素值的十进制表示为97，用二进制表示为“01100001”。由加密密钥生成的8 位随机整数分别是2,1,3,4,8,6,7,5。也就是说，原始像素的4 个MSB 被移动到4 个LSB 中，同时原来的4 个LSB 被移动到4 个MSB 中，如图2所示。在完成位平面置乱的步骤后，这个被加密像素块的二进制表示为“00010101”，对应的像素值用十进制可表示为21。

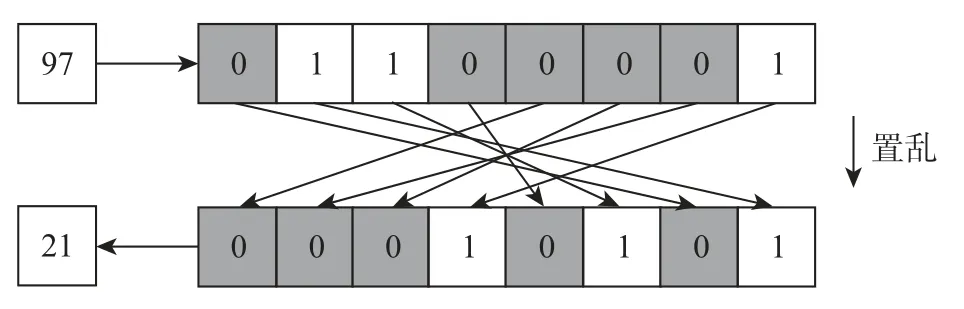
图2 位平面置乱示例（λ=4）Figure 2 Example of bit plane disordering (λ=4)

位平面置乱完成后，利用加密密钥Ke2对P个图像块的位置进行置乱，然后利用加密密钥Ke3对每个块内的S2个像素进行进一步置乱。需要注意的是，Ke3也是与每个块关联，由P个子密钥组成。

本文在图像加密阶段，以图像块为对象进行加密操作，这样做既保证了加密的有效性，又保留了足够的空间用于数据隐藏。

1.2 数据嵌入

在完成上述加密过程后，选择加密图像的λ位LSB 进行重构操作。被选择的位平面定义为Fl，其中l ∈{1,2,···,λ}。此时每一个Fl都是一个二值图像，大小和原始图像保持一致。然后将Fl分成P个不重叠的二值块，每个块的大小为S ×S。本文将由全1 或全0元素组成的块定义为均匀块（homogeneous blocks,HB），而将其他类型的块定义为非均匀块（non-homogeneous blocks,NB）。设置所有HB 的标签为1，而NB 的标签为0，于是所有的标签就可以构成一幅大小为(M/S)×(N/S) 的标签映射图（label map,LM）。具体LM 的生成方式如图3所示，假设位平面的大小为8×8，并且被分成2×2 大小的块，根据上文所述的块类型定义规则就可以获得一幅4×4 大小的LM。

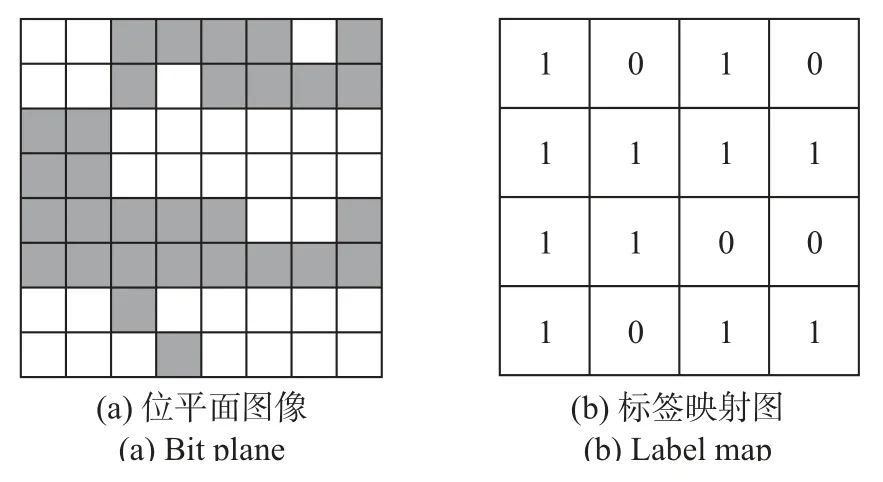
图3 生成标签映射图的示例图Figure 3 Example of generating label map

下面按照从左到右、从上到下的顺序对Fl进行逐块扫描。通过LM 可以获得两种块序列：由HB 构成的均匀序列和由NB 构成的非均匀序列。根据这两种块序列可以对所有的图像块进行重新排列，排列的规则如下：将所有的NB 排列在位平面图像的上部，而将HB 排列在下部。经过上述排列操作所得到的新图像被称为重构的位平面。对所有Fl进行重构之后即可得到最终的加密图像Ie。图4是一个位平面重构过程的示例图。

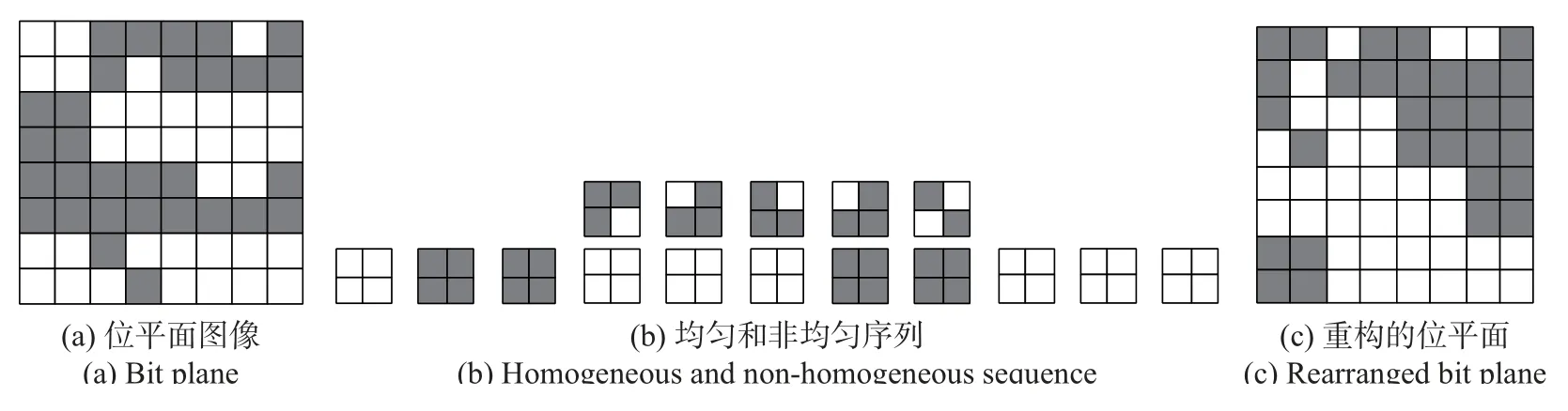
图4 位平面重构过程示例图Figure 4 Example of bit plane rearrangement

由于LM 的存在使得上述过程均可逆，也就是说，通过LM 可以恢复出原始的被选择的位平面Fl。另外，考虑到图像视觉质量的问题，额外数据嵌入到全黑或者全白区域会比嵌入边缘区域更好。翻转边缘区域的像素会比翻转全黑或全白区域的像素获得更好的视觉质量，但是全黑或全白区域的冗余性质能够帮助实现较高的嵌入量。以上结论貌似矛盾，但是本文提出的数据嵌入方案可以通过嵌入必要的辅助数据来解决这一矛盾。在本文的方案中，将LM作为辅助数据嵌入到重构的图像中，然后生成一个重构的自嵌入图像。因此，在加密图像中嵌入额外数据之前先嵌入辅助数据。

由于HB 由全黑或全白区域组成，因此在其中一个像素已知的前提下，这个HB 块中的其余像素可以被轻易推知，即如果一个HB 块中的一个像素是1 或0，那么这个块中的其余像素也一定是1 或0。因此，在保持一个像素不变的前提下，整个HB 块都可以被无误差地恢复。所以将每个HB 右下角的像素作为固定像素，并保持不变，即可通过直接替换原始像素的方式将LM 嵌入到除了固定像素之外的HB 块中。

由于LM 实际上是对大小为M ×N的位平面图像进行了S倍降采样所得，因此LM 的大小为MN/S2。根据线性扫描顺序对LM 进行比特流扫描，扫描所得的比特流就可以被嵌入到合适的位置。其中，比特流的长度等于LM 的尺寸，LM 比特流长度用LLM表示，且

用N1表示嵌入LM 比特流的块的数量，且

此外，为了保证数据提取和图像恢复时的可逆性，辅助数据是从第2 个HB 块开始嵌入的。将第1 个HB 作为指示块，保持不变，详细原因将在2.3 节中说明。随后，将LM 的比特流嵌入到N1个块中，这N1个块是从第2 个HB 块开始计数的。

图5是嵌入辅助数据的示例图。图5(a) 表示LM 扫描所得的比特流，即待嵌入的辅助数据。在图3中，标签映射图LM 的大小是4×4，因此LM 比特流的长度为16 比特。这些比特流信息依次被嵌入到重构的位平面中，如图5(b)所示，其中带有五角星标记的块表示第1 个HB，这个块始终保持不变，并不嵌入任何数据。从第2 个HB 开始嵌入记录位，如图5(c)所示。最后，剩余的可用块就可被用于嵌入额外数据。

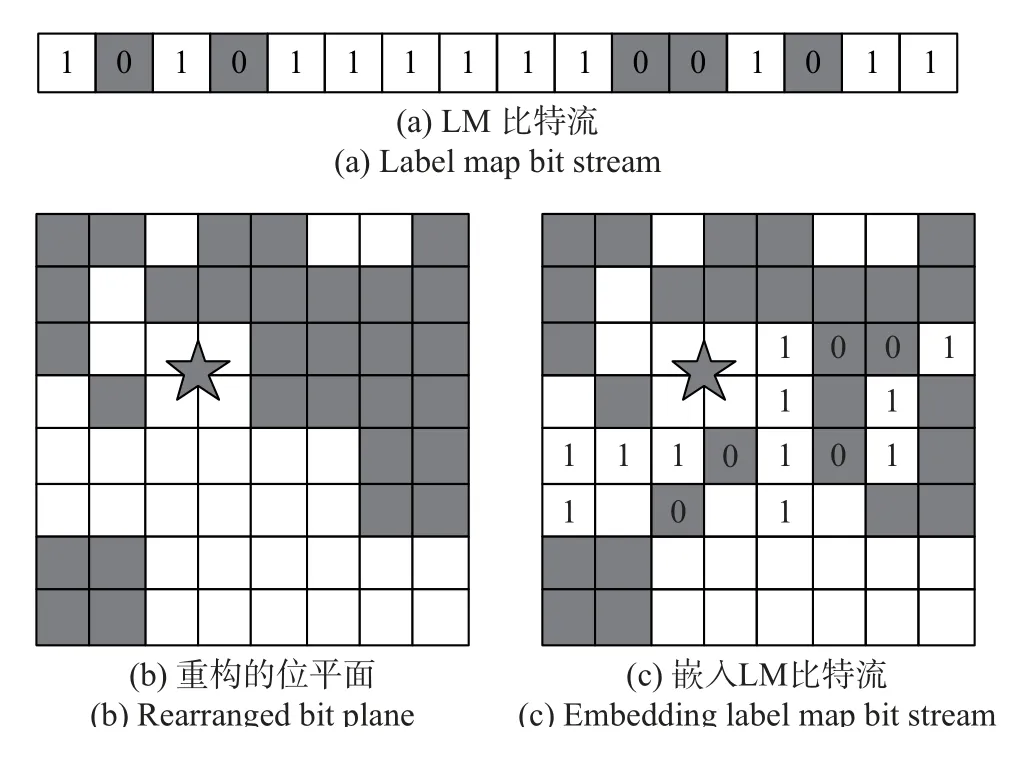
图5 嵌入辅助数据的示例图Figure 5 Example of embedding auxiliary data

对于数据隐藏者来说，额外数据是被嵌入到没有嵌入辅助数据的HB 中的。通过数据隐藏密钥Kh，数据隐藏者首先将额外数据w加密，得到we，并将被加密的额外数据we嵌入到剩余HB 块中。需要注意的是，这些块中的固定像素也不能被改变。N2表示可以用来嵌入额外数据的块数，且有

式中：N0表示所有HB 块数。由于第1 个HB 作为指示块不能被改变，所以计算可用于嵌入额外数据的块数时需注意这一点。

另外，单个位平面Fl的最大嵌入容量用Cl表示，在一个S×S的HB 中，右下角的固定像素不能被改变，则在一个HB 块中能够嵌入数据的比特数为S2-1，像这样的块共有N2个，于是Cl的值可以由式(6) 计算得到

位平面Fl的最大嵌入率Rl可以用式(7) 描述

在嵌入额外数据的过程中，数据隐藏者无法访问原始图像，在生成含密加密图像后，任何没有数据隐藏密钥的人都无法提取额外数据。上述的数据嵌入过程描述的是将额外数据嵌入到单个位平面，当在多个LSB 位平面内嵌入额外数据时，只需重复上述步骤即可。在多个LSB 位平面中嵌入额外数据时，本文方案的最大嵌入率R的计算公式为

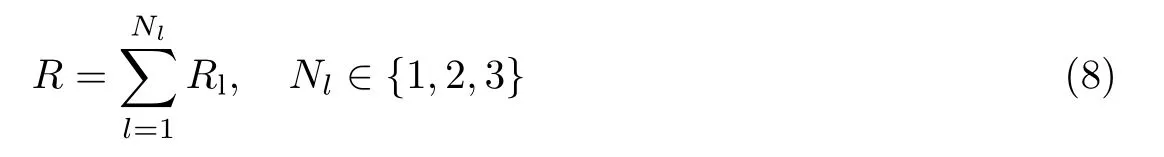
式中，Nl是指参与额外信息嵌入的位平面数。

上述的嵌入方案均采用最大化嵌入，即在所有满足嵌入要求的图像块中均嵌入额外数据。在能够实现某嵌入率的前提下，如需实现嵌入率任意可控，可根据Nl以及ERl代入上述步骤计算出给定的嵌入率对应的嵌入容量，再进行本节所述相关嵌入。

加密图像Ie中坐标为(i,j) 的像素定义为Fi,j，而Fi,j,l是Fi,j的第l位，则有

加密图像Ie的第l个位平面Fl在嵌入数据后变为F′l。是F′l中坐标为(i,j) 的位，因此含密加密图像Iew中坐标为(i,j) 处的像素表示为，且有

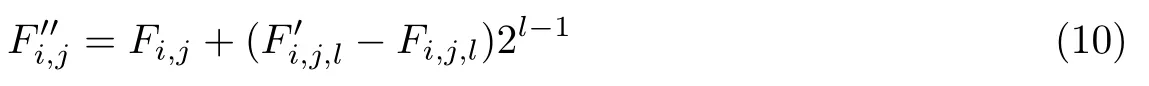
1.3 数据提取和图像恢复

图6大致描述了数据提取与图像恢复的流程。得到含密加密图像Iew后，接收者首先检索第l个位平面F′l，然后利用数据隐藏密钥Kh提取额外数据，最后通过加密密钥Ke恢复出原始图像Io。此外，也可以通过一定方式获得直接解密图像Iw，在视觉感受上，Iw看起来和原始图像Io非常相似。

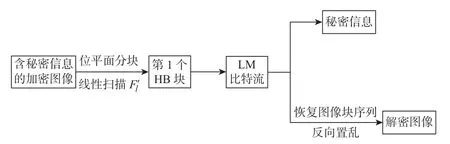
图6 数据提取与图像恢复的流程框图Figure 6 Flowchart of data extraction and image recovery

利用Kh可以实现额外数据的提取，对于Iew中的第l个位平面F′l，也是大小为M ×N的二值图像，接收者可以将其分成P个大小为S×S且不重叠的块B′r(r=1,2,···,P)，其余步骤描述如下：

首先，接收者按线性扫描顺序对位平面F′l进行扫描，以获取第1 个HB 的位置。如上所述，这个块在整个过程中都是保持不变的，所以这个块可以被当作一个指示块，用来区分位平面中哪一部分是NB，哪一部分是HB。或许在嵌入过程中会有某些HB 变为NB，又或许某些HB 的像素值在嵌入完成后没有发生改变，只要有这个保持不变的指示块存在，即可保证可逆性。

其次，接收者读取N1个块中除固定像素外的MN/S2比特位，可提取出LM 的比特流信息。

最后，通过定位余下的图像块就可以提取出嵌入的额外数据。

利用Ke可以对含密加密图像Iew进行解密操作，来得到与原图Io高度相似的解密图像Id，具体步骤如下：

步骤1先提取出辅助数据，即标签映射图比特流。并根据这些HB 块中右下角的固定像素恢复出原始图像块。

步骤2在获取到LM 的比特流之后，能够恢复出图像块的原始序列，那么就可以获得置乱后的加密图像。

步骤3在F′l中的所有块都回到原始的位置后，开始执行图像加密的逆操作，即反向像素置乱、块置乱和位平面置乱。通过加密密钥Ke1，Ke2和Ke3可以得到嵌入额外数据的解密图像。因为失真较低，所以所得图像在视觉效果上与原始图像相似。

除此之外，如果加密密钥Ke和数据隐藏密钥Kh都可用，则接收者可以从上述含密加密图像中提取额外数据，也就是在加密域中实现数据提取。如果接收者想要先解密图像再进行数据提取，则可以进行如下操作：直接解密图像后获得标签映射图和类噪声的重构自嵌入图像，再提取额外数据。通过这种方式能实现解密域的数据提取。

2 实验结果与分析

为了验证本文方案的有效性，选取了一些标准测试图像进行实验。下面将从4 个方面列出实验结果和分析结果：1）实验结果；2）安全性分析；3）参数变化分析；4）与其他方法的对比分析。

2.1 实验结果

如1.2 节所述，数据隐藏端可以从加密图像Ie的λ层LSB 中任意选择一些位平面来嵌入数据。因此，为了达到较高的嵌入率，数据隐藏者可以选择加密图像的λ层位平面（如：F1,F2,···,Fλ）进行数据嵌入。

图7(a) Lena 是一幅512×512 的标准灰度图像，图7(b) 为经过块/像素置乱、位平面置乱后对应的加密图像Ie。可以看到，加密后图像的视觉内容被有效隐藏。这里设置图像块大小为2×2，即S=2；λ设定为3。对于Io中的每个块在位平面置乱过程中，3 位MSB 被随机地移动到3 位LSB，同时5 位LSB 被随机移动到5 位MSB。图7(c) 是含密加密图像Iew，它是由加密图像Ie的3 位LSB（即F1、F2和Fλ）嵌入数据后得到的，嵌入率τ=1.075 00 bpp。图7(d) 是直接解密图像，其峰值信噪比（peak signal to noise ratio,PSNR）为50.183 dB；图7(e) 是对应的解密图像，PSNR 为无穷大，说明直接解密图像与原始图像完全相同。

图7 Lena 图的实验结果Figure 7 Experimental results of image Lena

2.2 安全性分析

本文中的图像加密方法包括位平面置乱、块/像素置乱和位平面重构。为了证明该方案的安全性，从图像直方图、熵和密钥空间几个角度进行了分析。

图8是Barbara、Lake、Lena、Aerial、Baboon 这5 幅标准测试图像加密前后的直方图。图8中的第1 列是5 幅原始图像，第2 列和第3 列分别是这些原始图像和对应的加密图像的直方图。从图像直方图的分布可以看出，加密后像素值的分布趋于均匀，说明了本文加密方法的有效性。

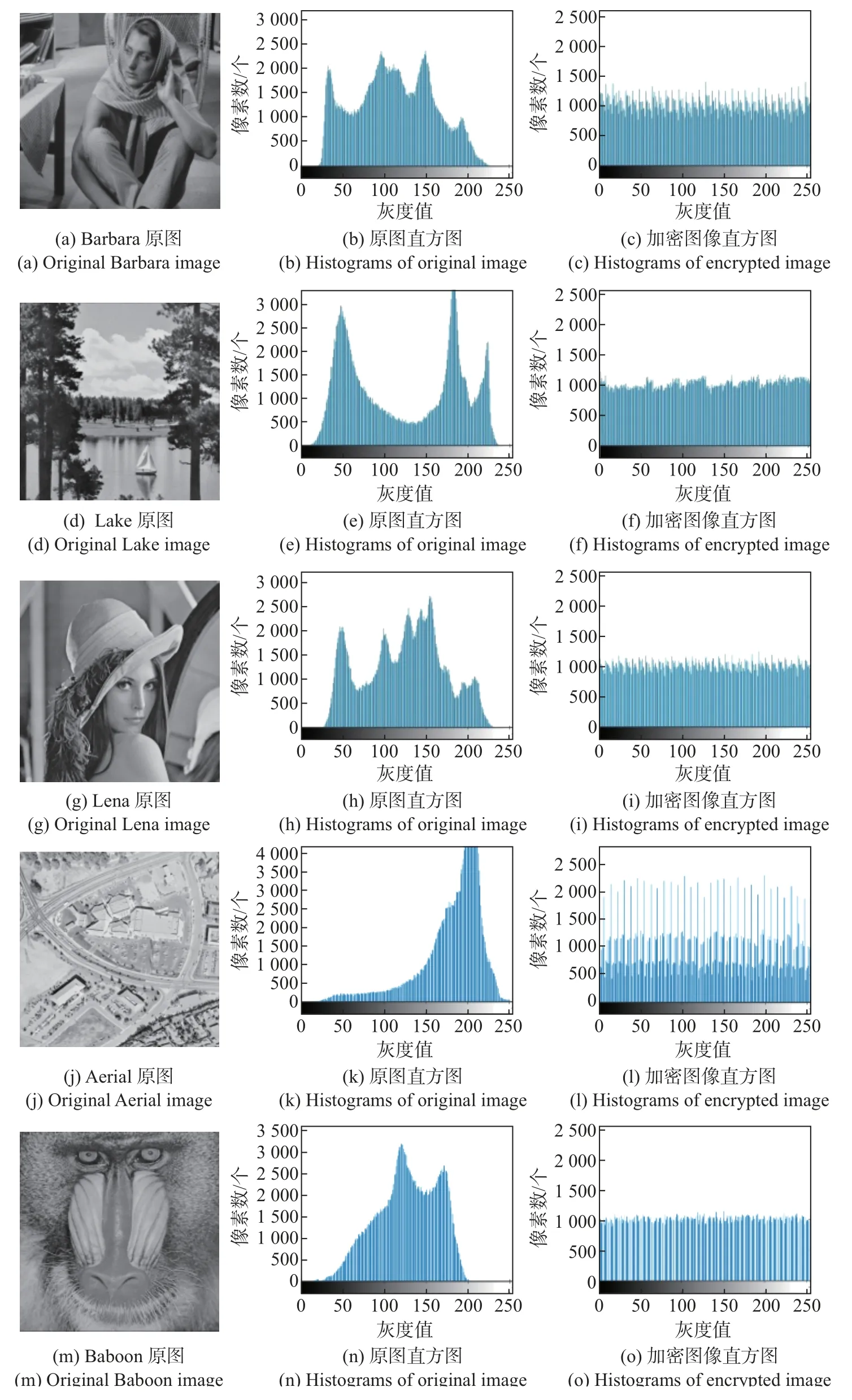
图8 图像加密前后的直方图Figure 8 Histograms before and after encryption

众所周知，信息熵可以用来衡量信源的随机性，计算公式为

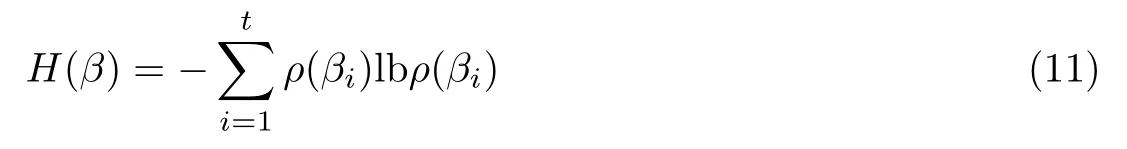
式中：β信源包含了t个符号，即β1,β2,···,βt，而ρ(βi) 表示每个符号βi发生的概率。显然，信息熵的值越大，系统的随机性和不确定性就越大。灰度图像的熵H最大值为8 比特，并且复杂性、随机性越大的图像其熵也就越大。表1列出了不同图像加密前后的熵值，很显然，加密图像的熵值均大于原始图像的熵值。

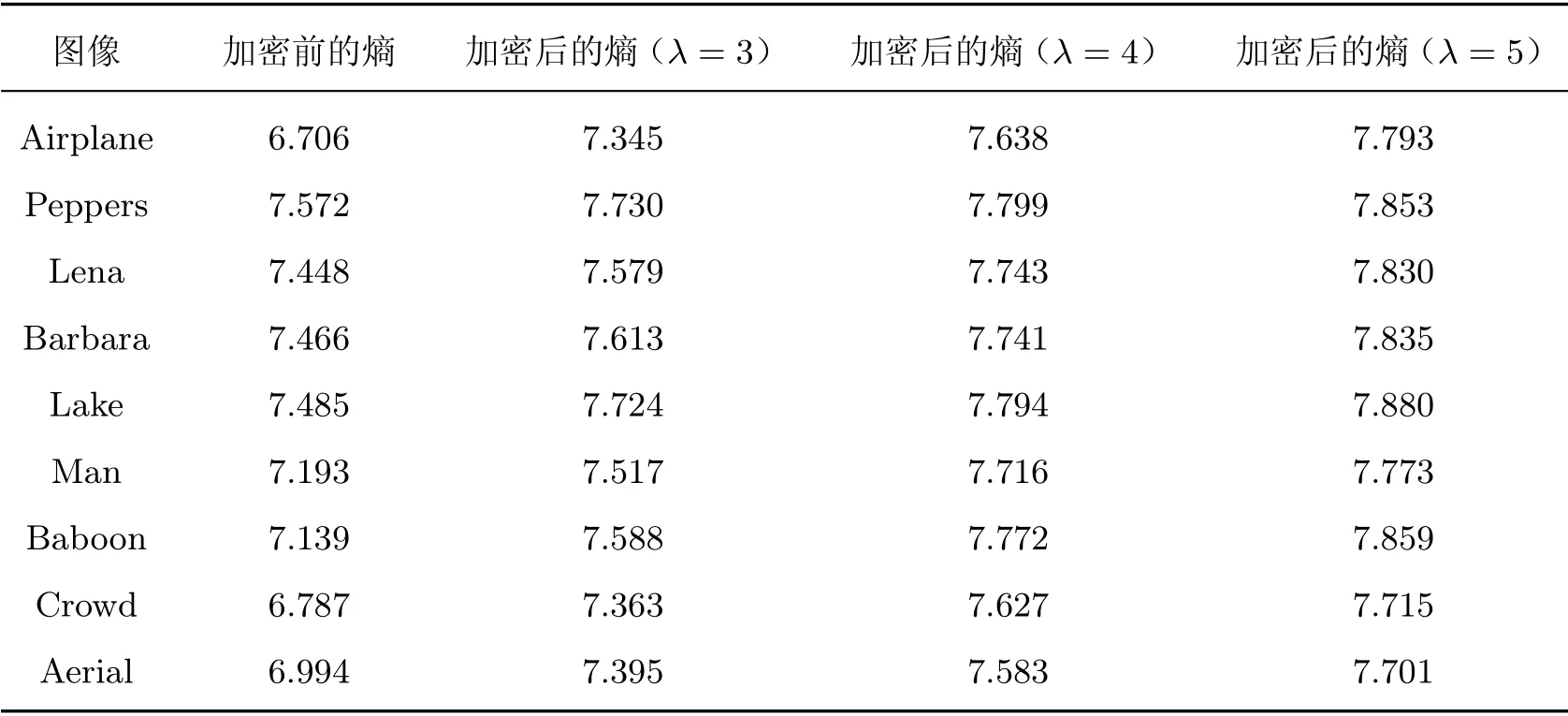
表1 不同图像加密前后的熵值Table 1 Entropies before and after encryption for different images bits

除了上述对图像直方图和熵的分析外，本文还将从密钥空间的角度对加密安全性能进行分析，包括以下几点：1）位平面置乱的加密密钥Ke1；2）图像块置乱的加密密钥Ke2；3）像素置乱的加密密钥Ke3；4）图像块的大小S×S。因此对于一个M×N的原始灰度图像而言，若图像块的个数为P=MN/S2，则对于所有块来说，位平面置乱有φ1种可能性，公式为

块置乱有φ2种可能性，公式为

像素置乱有φ3种可能性，公式为

因此，本文图像加密方法的所有密钥空间组成为

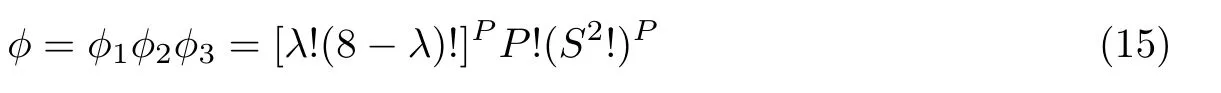
此外，通过伪随机数发生器，加密者只需一个种子即可生成所需的随机数作为置乱密钥，而无须顾虑复杂的置乱密钥所占字节会超过隐藏信息的字节数。一般来说，φ是一个非常大的数字，原始像素和加密像素之间几乎不可能直接建立一对一映射，确保图像加密的安全性和图像内容所有者的隐私性。对于一个512×512 的原始图像而言，当不重叠分块的大小为2时，共有个不重叠图像块，假设加密图像时选定λ=4，则整个密钥空间表示为

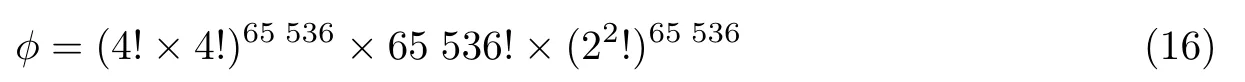
2.3 参数变化分析

本方案中有2 个重要的参数，即块大小S×S和进行位平面置乱的MSB 的层数λ。在表2～5 中，分析对比了本文方案在参数S和λ变化时直接解密图像的嵌入率τ和峰值信噪比PSNR 的值。

表2列出了S=2 时，不同λ下的直接解密图像的嵌入率和峰值信噪比。从表2中可以看出，大多数图像在λ值越大时，能达到更高的嵌入率。只有Baboon 图像在λ=4 时的嵌入率小于λ=2 和λ=3 的嵌入率。原因在于，当高4 位MSB 平面被移动到低4 位LSB 平面时，更多的非均匀块引起实际嵌入率偏低。此外，从表2中还可以看出，平滑图像的嵌入率比纹理图像的更高，这时因为平滑图像的均匀块更多，而纹理图像的非均匀块更多。

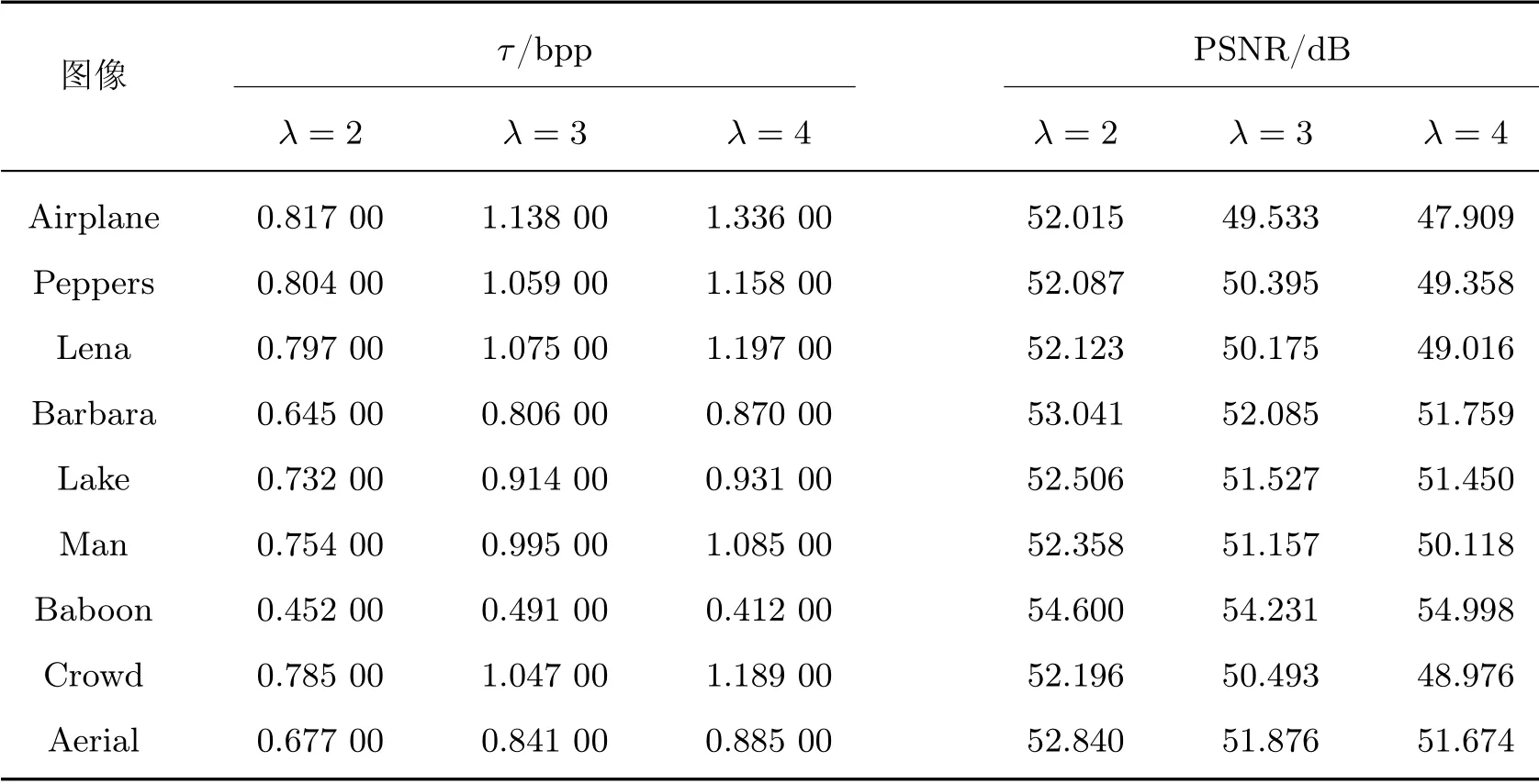
表2 不同λ 的直接解密图像的嵌入率和峰值信噪比（S=2）Table 2 Embedding rate and PSNR of directly decrypted images with different λ(S=2)

在表3～5 中，列出了λ=3 且块大小S变化时直接解密图像的嵌入率和峰值信噪比的值，对应3 种情况：{F1},{F1,F2},{F1,F2,F3}分别被用于数据嵌入。显然，用于数据嵌入的LSB 层数越多，嵌入率就越高，直接解密图像的PSNR 就越低。从以上实验中可以看出，嵌入率随着图像块大小的增加而降低，这是因为块越大，均匀块的数量就越少，所以用于数据嵌入的空间就越小。

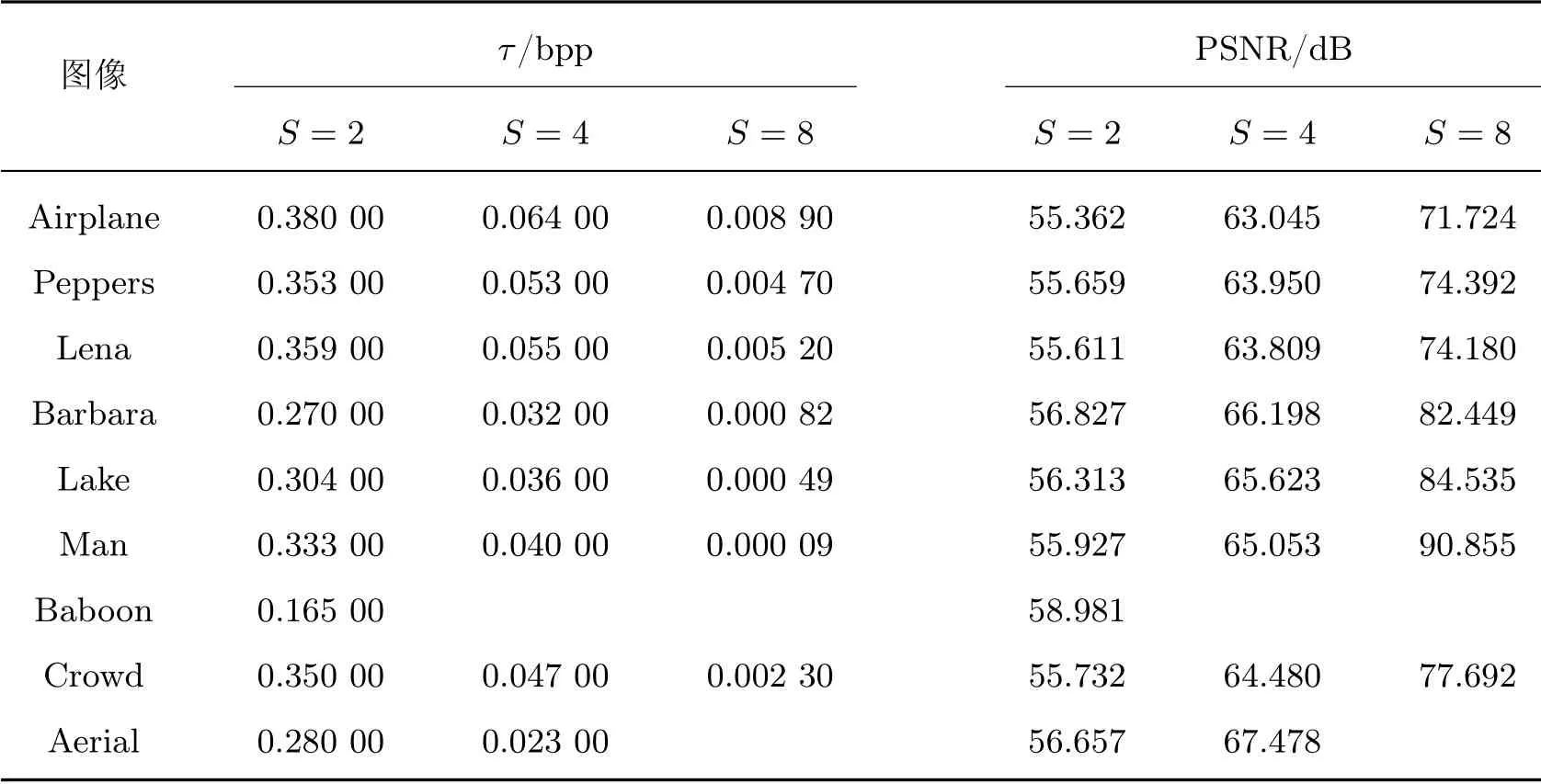
表3 不同S 的直接解密图像的嵌入率和峰值信噪比（F1 用于嵌入数据）Table 3 Embedding rate and PSNR of directly decrypted images with different S(F1 is used for embedding)

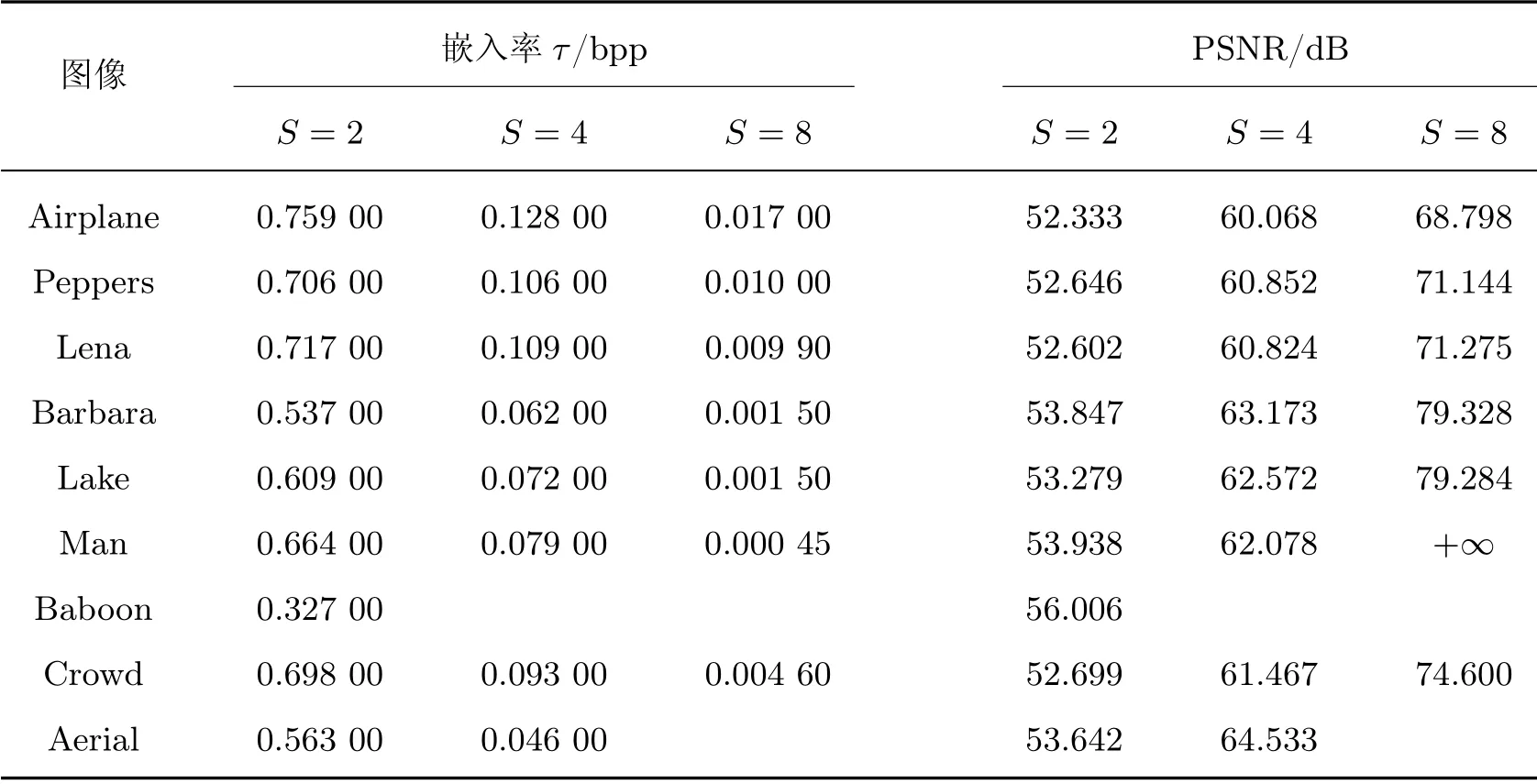
表4 不同S 的直接解密图像的嵌入率和峰值信噪比（F1,F2 用于嵌入数据）Table 4 Embedding rate and PSNR of directly decrypted images with different S(F1 and F2 are used for embedding)

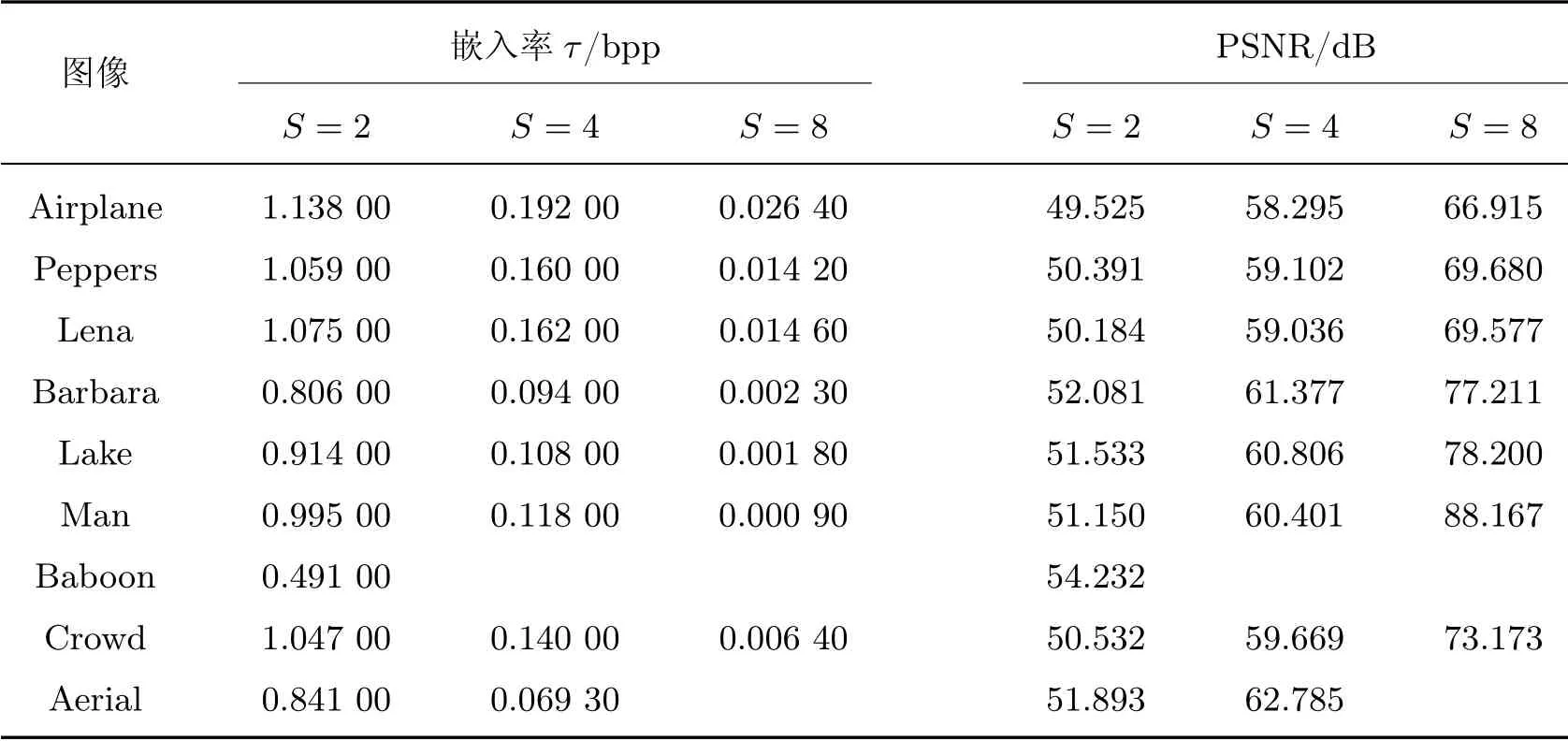
表5 不同S 的直接解密图像的嵌入率和峰值信噪比（F1,F2,F3 用于嵌入数据）Table 5 Embedding rate and PSNR of directly decrypted images with different S(F1,F2 and F3 are used for embedding)

2.4 与其他方法的对比分析

为了验证本文方法的有效性，在下文中与文献[17,28-29,34-36]的方法进行了对比分析。为了保证公平性，上述文献选择的实验参数均为各方案达到最优效果时的参数值，具体如下：文献[17,34-36]中图像块的大小分别设为4、2、2、2；文献[28]中选择3 层LSB；文献[29]中K-SVD 的迭代值设为50。本文方法的参数如下：S=2、λ=3，F1、F2、F3用于嵌入数据。

图9中的(a)～(d) 分别是大小为512×512 的Lena、Airplane、Baboon 和Peppers 在不同嵌入率下，解密图像的PSNR 值。设置本文算法中参数S及λ的值，可以得到不同的嵌入率。从以下实验结果图中可以看出，本文算法的曲线在坐标横轴上的范围较大，说明其能够达到更高的嵌入率；而在嵌入率相同的情况下，本文方法得到的直接解密图像的PSNR 均优于对比的其他文献方法的指标。综上所述，本文的方法比文献[17,28-29,34-36]的方法具有更好的率失真性能。此外，纹理度较复杂的图像的嵌入率比平滑图像的低，这一点在图9中的(a)～(d) 中也能看出：使用本文算法的Baboon 图像的最大嵌入率达到0.491 00，而其他平滑图像的最大嵌入率都大于该数值。

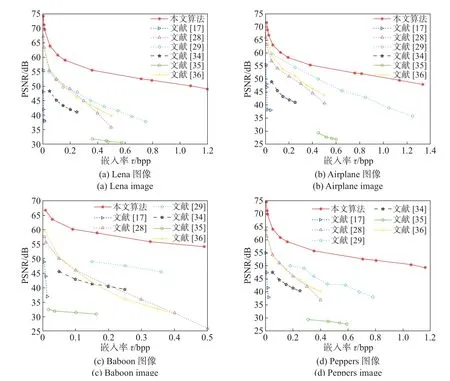
图9 直接解密图像的PSNR 对比图Figure 9 Comparisons of PSNR for directly decrypted image

在图像恢复过程中，本文的方法与文献[28-29,35-36]的方法都可以实现完全可逆恢复，而文献[17,34]的方法在恢复的图像中可能存在一些错误。表6给出了本文方案与文献[17,34]在不同嵌入率下恢复图像视觉质量的比较结果。可以发现，在给定的嵌入率下，本文方案恢复图像的PSNR 值为无穷大，优于文献[17,34]的方案。换句话说，本文的方法能够以可逆且无损的方式恢复图像。

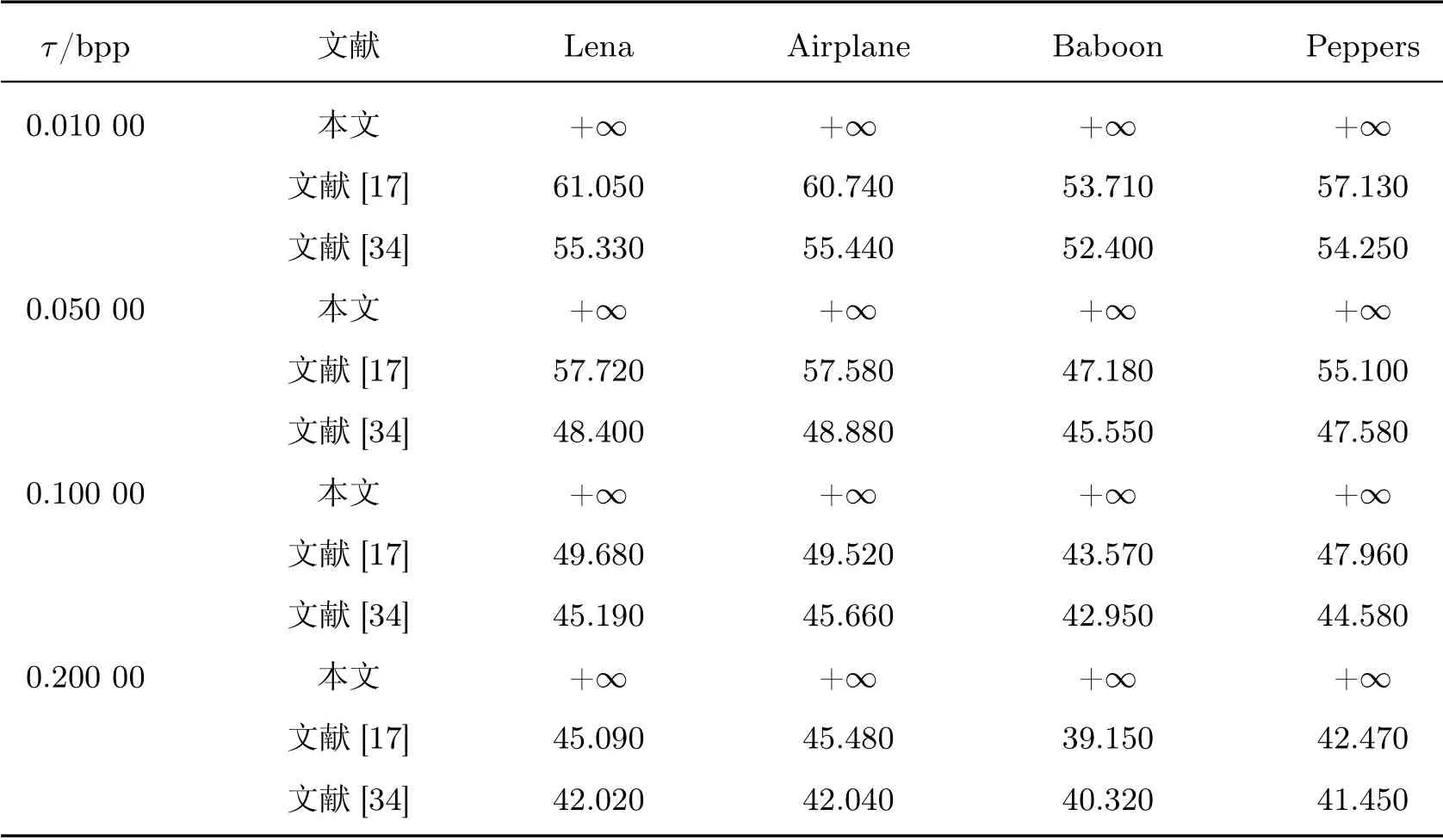
表6 恢复图像的PSNR 值的对比Table 6 Comparisons of PSNR for recovered image

3 结 语

本文提出了一种基于二进制块重构的可逆信息隐藏方案。对于每个块，通过特定的图像加密方法，MSB 平面与LSB 平面随机重排；然后对块和像素进行置乱以提高安全性。数据隐藏者可以通过重新排列二进制块将其他数据嵌入到加密图像的LSB 中。接收端可以根据密钥的可用性分别进行数据提取、图像解密和图像恢复。实验和分析表明，该方案在保护原始图像隐私方面具有较高的安全性，实现了高嵌入率，获得了高质量的直接解密图像，并且在整个过程中准确率高。