一种基于双重网络模型的单幅图像超分辨率方法
倪翠,王朋,张广渊,李克峰
山东交通学院信息科学与电气工程学院,山东济南250357
图像超分辨率(image super resolution,ISR)重建是计算机视觉中提高图像和视频分辨率的一类重要图像处理技术,其目的是由低分辨率(low resolution,LR)图像生成具有丰富细节信息和较高分辨率的高分辨率(high resolution,HR)图像,而不是简单地获得更大尺寸的图像[1-3]。图像超分辨率技术根据不同的对象可分为三类:多幅图像超分辨率、视频序列超分辨率、单幅图像超分辨率。
目前,针对单幅图像的超分辨率(single image super-resolution,SISR)重建的方法大致可以分为三类,即:基于插值的方法、基于重构的方法、基于学习的方法[4]。这里,基于学习的超分重建方法使用最广泛,效果最好。该方法包含基于邻近点特性的方法[5]、基于稀疏性的方法[6]、通过自学习的方法[7]、局部线性回归[8]和基于深度学习的重建方法等。
近年来,利用深度学习技术进行图像超分辨率重建技术的研究取得了显著进展,文献[10]最早提出了利用超分辨率卷积神经网络(super-resolution convolutional neural networks,SRCNN)实现单幅图像超分重建的方法;文献[11]提出了高效亚像素卷积神经网络(efficient sub-pixel convolutional neural network,ESPCN)的重建方法;此外,还有许多其他优秀算法[12-16]。
本文以单幅图像为研究对象,对深度学习领域中的高效亚像素卷积神经网络算法进行了改进。通过调整网络构造结构,进一步结合深度学习中的残差网络知识,提出了一种优化的双重网络超分方法。通过实验证明,该算法在一定程度上能够有效地提高单幅图像超分辨率重建的精度。
1 基于深度学习的单幅图像超分方法介绍
1.1 基于卷积神经网络重建方法
Dong等[9-10]最早将卷积神经网络应用于图像超分辨率重建问题,构建出一种3层的超分辨率卷积神经网络模型的方法,称为SRCNN方法。主要步骤为:首先对低分辨率图像进行一次预处理,然后通过双三次插值的方法将低分辨率图像放大至与目标图像相同分辨率的尺寸,最后将此过程图像作为模型的输入,通过网络模型实现特征提取(feature extracting)、非线性映射(non-linear mapping)等操作获得指定放大倍数的高分辨率目标图像。SRCNN模型网络结构示意图如图1所示。

图1 SRCNN模型网络结构示意图Figure 1 Schematic diagram of SRCNN model network structure
1.2 深度递归卷积神经网络
因SRCNN的层数较少和感受视野较小等问题,文献[12]提出了一种深度递归卷积神经网络(deeply-recursive convolutional network,DRCN)重建方法。该方法由3层网络模型构成,分别为嵌入层网络(embedding network)、推断层网络(inference network)、重建层网络(reconstruction network)。DRCN的3层网络与SRCNN的功能是一一对应的,即嵌入网络实现对原始低分辨率图像的特征提取,进而通过推断网络建立起非线性映射关系,最后实现单幅图像的超分辨率重建。
DRCN算法中的推断网络是一个递归网络,相当于多个卷积层串联在一起。该算法的缺点为:随着网络层数不断加深,容易产生梯度爆炸/消失问题。为了解决这一问题,文献[13]采用梯度监督和跳跃连接(skip connection)的知识来弥补该算法的缺陷。图2为DRCN模型网络结构的示意图。
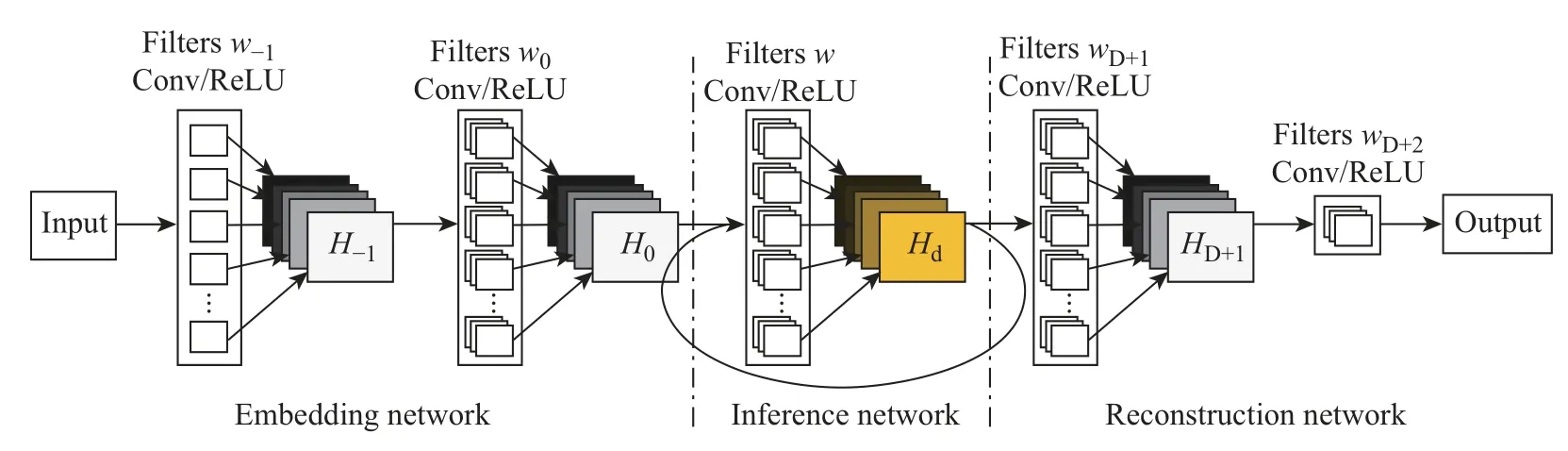
图2 DRCN模型网络结构示意图Figure 2 Schematic diagram of DRCN model network structure
1.3 高效亚像素卷积神经网络算法
SRCNN等方法在实现过程中需要对原始低分辨率图像进行双三次插值得到放大后的图I′。此时,以I′作为初始值会增加整个超分重建过程的运算量,导致运算效率明显降低。于是文献[11]提出了一种基于高效亚像素卷积神经网络模型。该模型可直接将原始图像作为输入对象,输入模型后经由L层(L≥2)卷积神经网络得到的结果应用亚像素卷积层进行特征映射,获得指定扩大倍数的高分辨率图像。
图3为原ESPCN模型网络结构的示意图。前一部分隐藏层(如图3中的左半部分hidden layers)是由L层网络构成的,其作用是通过特征提取得到指定放大倍数r的平方倍通道数的特征图。后一部分亚像素卷积层(如图3中的右半部分sub-pixel convolution layer)是一种上采样方法,目的是将低分辨率图像上采样到高分辨率图像。这是一种较适于超分辨率任务的方法。简单来说,该方法的思想是若要将目标图像进行r倍放大,需要已知相应的r2幅特征图,对r2幅特征图像进行组合得到1幅超分重建图像。

图3 ESPCN模型网络结构示意图Figure 3 Schematic diagram of ESPCN model network structure
2 本文研究方法
传统的ESPCN算法相比于SRCNN算法,主要是在速度上的提升。从图3可以看出,ESPCN算法中的隐藏层(hidden layer)是由比较简单的单网络层组成的,容易造成图像边缘细节特征的丢失。针对该特点,为了得到细节更为丰富的超分图像,本文拟引入复杂的双重网络层,进一步优化ESPCN网络结构,提高图像超分辨率重建的精度。
图4为本文改进后的ESPCN网络模型结构示意图,该模型由2个并联的网络构成。上层网络结构与原ESPCN网络模型隐藏层部分基本相同,即由L层卷积层构成(L=2)。下层网络结构由带组归一化(group normalization,GN)卷积层和残差网络两部分组成。
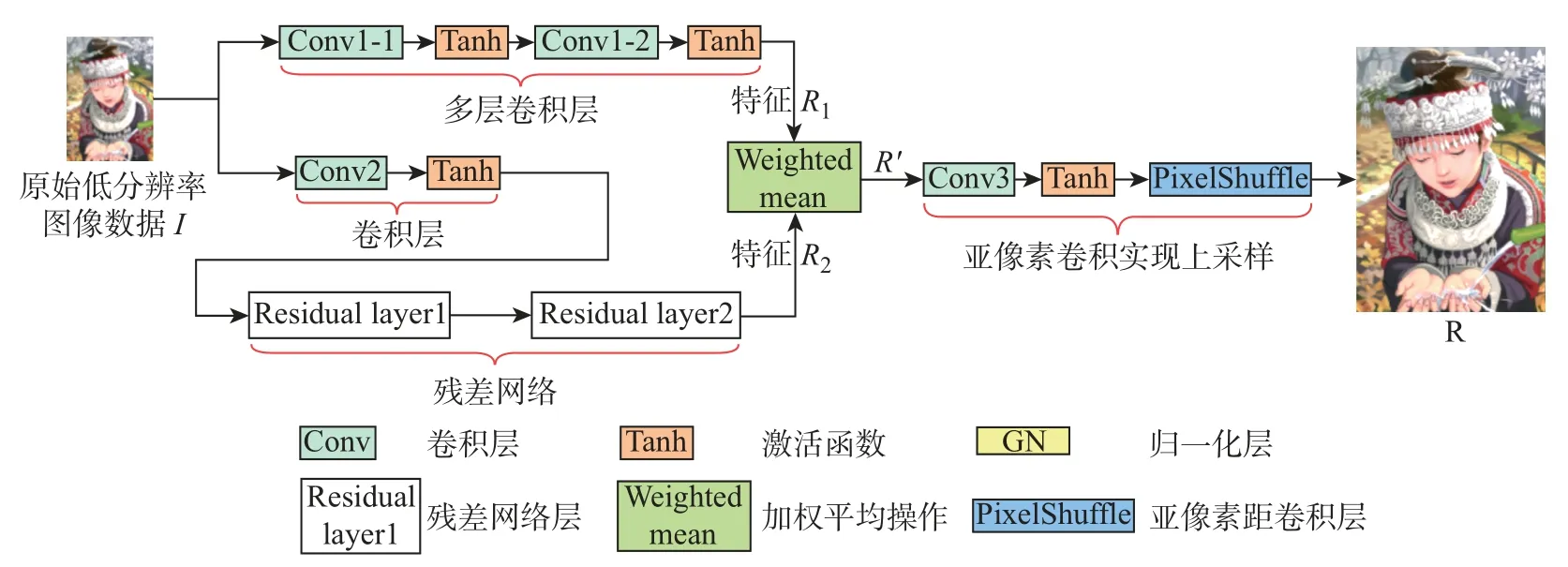
图4 本文双重模型网络结构示意图Figure 4 Schematic diagram of the dual model network structure in this article
本文研究方法的具体步骤为:
步骤1原始低分辨率图像数据I经过上层网络训练后,得到其特征R1。
卷积层covn1-1采用64个卷积核(f ilter),卷积核大小(kernel_size)为5×5。卷积层covn1-2采用32个卷积核,卷积核大小为3×3。激活函数采用Tanh()函数,其函数形式为

步骤2I与下层网络训练后,得到其特征R2。
步骤3对R1与R2进行加权平均,得到过程结果R′。
步骤4对R′通过亚像素卷积层实现最终的超分辨率重建R,如图4所示。
卷积层covn3采用N个卷积核,卷积核大小为3×3。其中N的值为

式中:C为原图像通道数;r为扩大倍数。
激活函数采用Tanh()函数,PixlShuffle层实现特征图转目标图。下面将具体介绍本文方法中的步骤2和3。
2.1 带组归一化的卷积层
在卷积神经网络中,归一化层具有防止梯度爆炸和梯度消失的作用。根据批处理样本数量N的大小,选择合适的归一化类型。本文设置的样本数量较小,故选用的归一化层为带组归一化(GN),即在原卷积层后加上GN,让后续残差网络获取更多的特征信息。
带组归一化的卷积层(图4中“带GN的卷积层”所示)具体执行过程如下:
首先提升卷积层的卷积核数量,即卷积核由原来的64个增加至128个,该做法可以得到更多的细节信息。然后添加GN层,使下一层输入数据的均值与方差能够固定在一定范围内,从而能更快地找到最优解。
这里,归一化层GN通道数为128,组数为4;激活函数采用Tanh()函数。
2.2 残差网络
残差网络是由一系列的残差块组成的,可以解决由于网络深度增加而带来的收敛问题。本文的残差网络模型由2个残差网络层构成,第1个残差网络层的输入通道数为128,输出通道数为64,残差块数量为2。第2个残差网络层的输入通道数为64,输出通道数为32,残差块数量为2。残差网络内使用的激活函数为ReLU()函数,其函数形式为

式中:x为输入数据。
图5为残差网络层的结构示意图,由2个残差块组成。具体解释如下:

图5 残差网络层结构图Figure 5 Structure diagram of the residual network layer
在第1个残差块中,输入数据x分别通过卷积层conv 2-1和conv 2-2,采用激活函数ReLU得到降维后的特征图像F1。由于该残差块中输入通道和输出通道的维数不同,对x进行1×1的卷积降维操作后的结果记为F′1。随后对F1和F′1进行简单的单位加操作。对上一步结果进行激活,得到第2个残差块的输入数据。
在第2个残差块中的具体操作与第1个残差块步骤相同。
2.3 加权平均操作
上层网络训练后得到图像特征的整体信息R1,下层网络训练后得到图像特征的高频信息R2,即细节信息,如图4所示,因此本文采用加权平均的方法,将更多细节信息添加在上层的整体信息中,从而获取到精度更高的超分结果。
在图4中,R1为图像特征的整体信息,既包含低频信息,也包含高频信息,R2为下层网络训练后得到的高频信息,通过加权平均的方式调整优化原有图像特征中的高频信息,从而得到整体较好的超分辨率分效果。考虑到整体和局部的特点,根据主观经验法对权重进行分配,其选取原则为:R1的系数远大于R2,且二者系数之和为1。因此,加权平均的系数分别选取(0.7,0.3)、(0.8,0.2)、(0.9,0.1)3组值进行实验,结果显示,系数组(0.8,0.2)的超分辨率重建效果最佳。故式(4)中R1和R2的系数选用0.8和0.2,由此可以得到最终改进优化后的超分辨率图像R′为

3 实验及分析
针对不同的超分倍数,本文选用了双三次插值、SRCNN、ESPCN和本文算法进行实验,从主观和客观两个层面来描述各个算法的超分辨率重建效果。这里,实验模型搭建和训练均采用了Pytorch框架。客观层面则采用峰值信噪比(peak signal-to-noise ratio,PSNR)和结构相似性(structural similarity,SSIM)两个指标进行评估,二者的数值越高,说明重建效果越好。
3.1 实验数据集
本文采用Timofte数据集的91幅图片作为原始数据,选择其中65幅图片作为训练集,26幅图片作为验证集。测试集采用公用基准数据集Set5、Set14、BSD100和urban100。如图6所示,为原始图像中的部分图像。

图6 原始数据中的部分数据Figure 6 Parts of the original data
3.2 实验结果及分析
图7和8分别对数据集鹦鹉和鲜花进行了2倍的超分重建效果,图9为数据集湖泊的3倍超分重建图像,图10为数据集后视镜4倍超分重建图像。实验中,分别选用双三次插值、SRCNN、ESPCN和本文双重网络下的ESPCN算法这4种方法进行实验。为了进一步说明各算法的重建效果,将超分辨率重建图像的局部部位进行了单独显示,如图7~10中超分图像的右下角所示。在图7~10中,LR为原始低分辨率图像,HR为原始高分辨率图像,用以检测超分方法的效果。

图7 Set5-鹦鹉超分辨率2倍后的重建效果图Figure 7 SR images of the Set5-parrot in twice

图8 Set14-鲜花2倍对比图Figure 8 SR images of the Set14-f lower in twice

图9 BSD100-湖泊3倍对比图Figure 9 SR images of the BSD100-lake in three times

图10 Urban100-后视镜4倍对比图Figure 10 SR images of the Urban100-rearview mirror in four times
从主观层面上看,图7~10中双线性插值(Bicubic)超分后的效果最差,边缘细节比较模糊。SRCNN重建的效果优于双线性插值的效果,但是与ESPCN和本文算法的效果相比,略差一些。ESCPN算法与本文算法的超分重建效果相当,均优于双线性插值效果和SRCNN重建效果,但通过右下角显示的局部细节图来看,当超分重建倍数为2、3、4时,本文算法的重建效果均略优于原ESPCN的重建效果,特别是边缘细节部分较原ESPCN重建的边缘细节部分更为清晰。
从客观层面上看,本文选用了峰值信噪比(PSNR)和结构相似性(SSIM)两个客观指标对超分重建后的图像质量进行评价,计算所有放大倍数下超分重建图像的PSNR和SSIM值,如表1所示。从表1中可以得出,本文方法重建图像的PSNR和SSIM值均高于其余三种算法重建图像的PSNR和SSIM值。这说明,本文方法的超分重建效果优于双三次插值效果、SRCNN重建效果和原ESPCN重建效果,本文方法的重建图像质量更高一些,且最接近原始高分辨率图像。
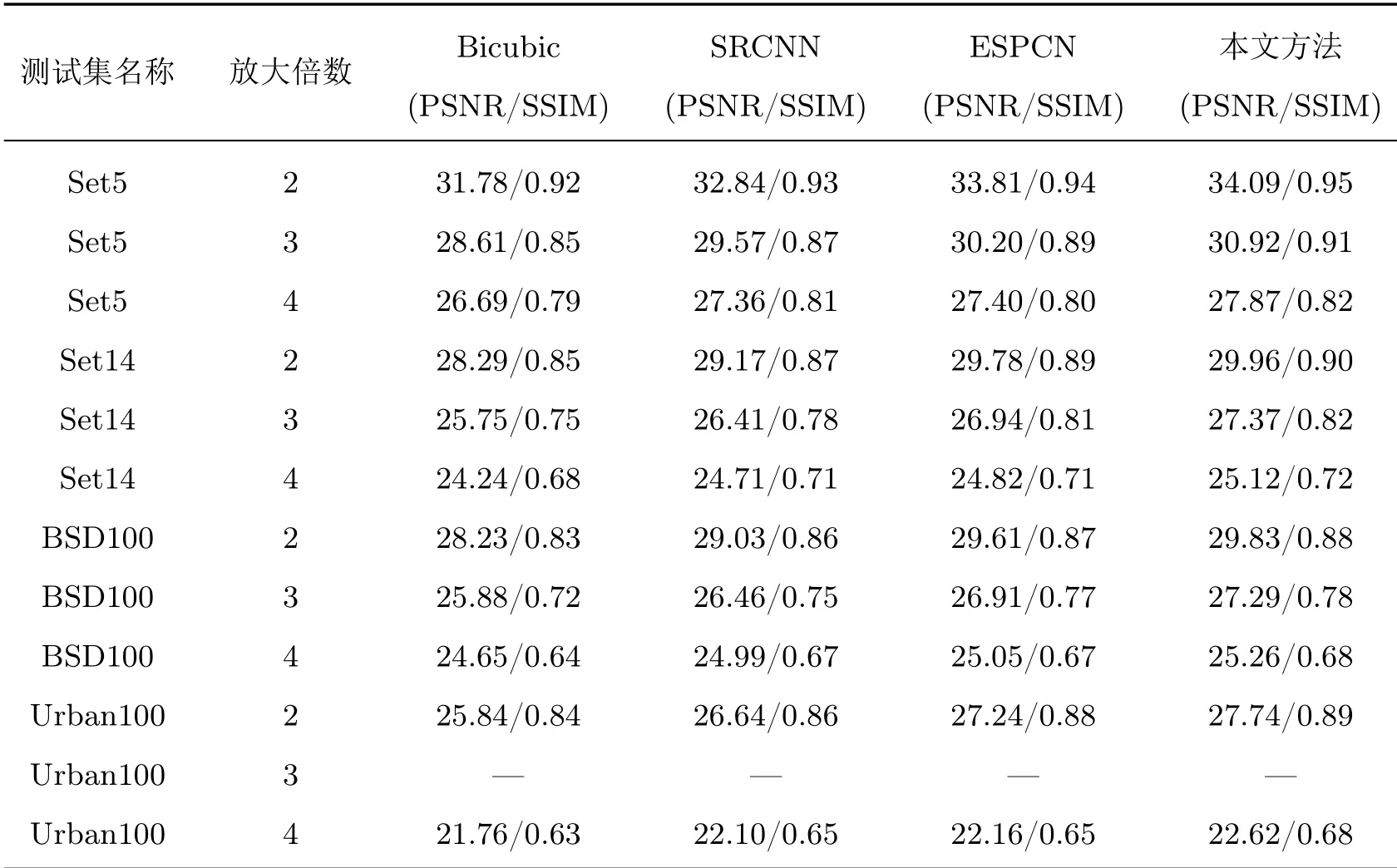
表1 不同算法下超分结果的客观评价Table 1 Objective evaluation values of different algorithms
图11为本文方法与原ESPCN方法在模型训练过程中loss值的变化曲线图,可以看出本文算法loss值比原ESPCN算法下降更快,由此可以说明该方法在实现过程中收敛速度更快,重建效率更优。
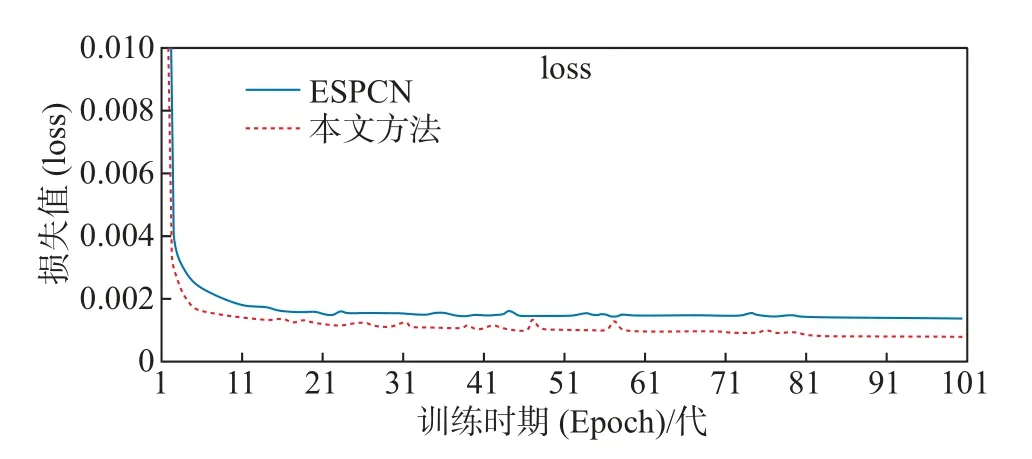
图11 本文方法与原ESPCN的loss值变化曲线Figure 11 Loss value change curve between the method in this paper and the original ESPCN
4 结语
本文提出一种对单幅图像超分辨率重建的改进算法,重点在于解决单幅图像的超分重建优化问题。通过改进原始ESPCN算法,增加一层残差网络模型,构成一种双重卷积神经网络模型,进而通过加权平均的方式获取图像中更多的细节部分,提高超分重建质量。实验结果表明,无论在主观层面上还是客观层面上,本文所提算法较原有ESPCN算法得到了较好的超分重建图像,特别是在局部细节部分,重建图像整体质量得到了较好的改善。

