冻融作用下污泥固化轻质土动力特性及结构演化

杨爱武 ，王斌彬 ，钟晓凯

（1.东华大学环境科学与工程学院，上海 201620；2.天津城建大学天津市软土特性与工程环境重点实验室，天津 300384）

随着城市化的加速发展，城市污泥的生成量越来越多，对于环境的影响也越来越严重。污泥具有含水量高、有机质含量大的特点，且力学性质差，重金属含量高[1]。如若不加以处理，会对环境产生严重影响，甚至会危及人类健康。通过污泥固化技术，使污泥变成一种新型的污泥固化轻质土。世界上很多国家和我国北方大部分地区各类土体存在冻融循环现象。

国内外很多学者对冻融循环作用下各类土体动力特性做了很多研究，取得较多的成果[2-6]。如魏海斌等[5]对粉煤灰土进行冻融循环后的动三轴试验，发现3次冻融循环后粉煤灰土动力性能指标优于粉质黏土，具有良好的稳定性和抗冻性。卢连长等[6]发现冻融过程中力学性质的变化不仅与土样的种类有关，也与土样的矿物成分有关，前10次冻融循环对高岭土及膨润土的长期强度影响很大。马玉涛等[7]对冻融循环作用下的路基粉质黏土进行动三轴试验，发现受冻融循环次数影响土体动强度、动黏聚力下降趋势明显，动内摩擦角有一定的下降趋势，但无明显规律性。Simonsen E.等[8]对冻融循环后的土进行动三轴试验，发现冻融作用对土体动弹性弹性影响显著。宋金华等[9]对冻融循环作用下的石灰改良土进行动三轴试验，建立了一个预测冻融循环和动应力共同作用下的累计塑性变形模型。孙静等[10]研究了冻融循环对粉砂土动力特性影响，并建立了一个动模量比与动应变关系曲线的归一化拟合模型，建议将冻融循环5次后的土体动力参数作为基本参数，进行动力反应分析。杨爱武等[11]发现污泥固化土静、动长期强度随冻融次数的变化规律基本一致，在其他条件相同的情况下，土体静长期强度明显大于动长期强度。王静等[12]对3种不同塑性指数的季冻区路基土进行冻融循环后的动三轴试验，发现季冻区路基土动弹性模量和动剪切模量的大小与围压和塑性指数正相关，与冻融循环次数呈负相关，在6次冻融循环后均趋于稳定。JIN Qing等[13]发现冻融循环有利于粉土阻尼比的增加，动剪切强度和动模量随冻融次数的增加而减少。

目前，有关冻融循环作用下土体动力特性的研究成果较为丰富，但是冻融循环作用下土体结构特性变化研究还不多见，另外针对污泥固化土的相关研究也很少。中国存在广大的多年冻土和季节性冻土区，这些地区的土体都遭受到不同程度冻融破坏，严重影响了工程质量，是冻土地区道路破坏的主要影响因素之一。本文对冻融循环作用下的污泥固化轻质土进行动三轴试验和固结试验，分析冻融循环作用对污泥固化轻质土动力特性和结构特性的影响，为污泥固化轻质土在实际工程的应用提供依据。

1 试验方案

1.1 试验材料

试样采用的污泥取自天津某污泥填埋场，伴有浓烈腐臭味，颜色呈黑褐色，呈流塑状。污泥从现场取回后，放置在阴凉处储存，并封箱覆盖防止雨水渗入和阳光直射。由于污泥本身强度低，加入适量的黏土以提供足够的土颗粒形成骨架结构，可以提高土体强度。黏土采用天津滨海新区的软黏土，将黏土捣碎成小块，在105 ℃温度下烘干24 h后研磨、筛除杂质，将处理好的黏土密封保存，防止受潮。污泥和黏土的物理指标见表1。其中发泡剂为铝粉，固化剂为石灰、水泥。试验采用的材料配比（质量比）见图1。

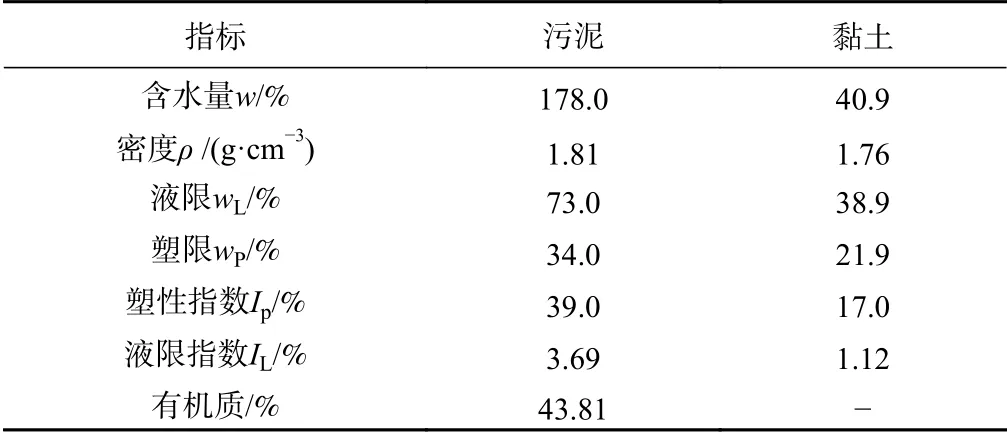
表1 试样物理特性指标Table 1 Physical characteristics of the soil samples

图1 材料配比饼状图Fig.1 Pie chart of the material ratio

1.2 试样制备

污泥固化轻质土（固化土）具体制备步骤如下：在有机玻璃管内壁涂刷1层凡士林，用胶带和透气不透水布将一端封闭。按照配比将材料混合搅拌均匀后倒入模具。为防止断层和较大空隙，需边倒入边振捣以排出空气。装土完成后，封闭另一端，放入养护箱中养护后完成并模。

污泥固化轻质饱和土试样（饱和土）制备步骤如下：将固化土放置在饱和罐中，在真空抽气容器封闭后用抽气管将饱和罐内的空气抽出，直至饱和罐内压力为-0.1 MPa，完成抽气。静置24 h至饱和罐内无气泡冒出，试样饱和。

污泥固化轻质重塑土（重塑土）制备步骤如下：将同一批次破碎后的固化土进一步碾碎，与水充分搅拌后用保鲜膜包裹，静置24 h后取出击实。击实后，用削土刀将土削成设计尺寸，包裹保鲜膜以防止含水率变化。

1.3 试验方案

1.3.1 冻融循环试验方案

将养护完成的固化土放入低温冷冻箱内，设置冻结温度，进行12 h低温冻结，之后取出并在室内放置12 h，即完成1次冻融循环。

考虑到天津地区冬季的低温波动、冻土深度以及路基厚度，试验冻结温度选择-5 ℃、-10 ℃、-15 ℃、-20 ℃。根据杨爱武等[14]对污泥固化土工程性质的研究，发现在养护28 d后，污泥固化土无侧限抗压强度趋于稳定。因此，选择固化土在标准养护条件下养护28 d后进行冻融试验。养护完成后，测得土体无侧限抗压峰值强度与冻融次数n（图2）。由图2可知，冻融循8次之后，无侧限抗压峰值强度趋于稳定。因此试验设置有限次冻融循环次数为0，1，2，4，6，8，10次。

图2 峰值强度与冻融循环次数n的关系曲线Fig.2 Relationship between the peak intensity and freezing-thawing cycle times n

1.3.2 动三轴试验方案

采用DDS动三轴仪对冻融循环后的污泥固化轻质土进行不固结不排水动三轴试验。污泥固化轻质土主要作为路基填料，考虑到交通荷载对路基土的影响，试验设置围压为40 kPa，波形为类似交通荷载的正弦波。交通荷载的频率与车速及交通工具有关[15]，设置频率为1 Hz。

试验设计为单轴循环加载方式，根据三轴剪切试验结果确定动应力幅值。按照《土工试验规程》SL 237—2019要求，确定破坏标准为轴向累计应变达到5%。由于已在文献[11]中研究了冻融循环对固化土累积变形的影响，表明随着冻融次数的增加，土体临界动应力降低，且动应力幅值相同时，固化土应变趋势基本一致。因此，本文着重研究冻融循环次数和冻结温度对污泥固化轻质土动应力-应变曲线、动强度、动模量以及结构性的影响。试验的具体方案见表2。

表2 试验方案Table 2 Test scheme

2 冻融循环作用下污泥固化轻质土动力特性

2.1 冻融作用对动应力-应变关系的影响

不同冻结温度和冻融循环次数下的污泥固化轻质土动应力-应变曲线见图3。从图3可以看出，在不同冻融循环次数下土体动应力-应变呈弹塑性应力应变关系。曲线表现为弱应变硬化型。同一动应力下，随着冻融次数的增加，动应变幅值也增大。前4次冻融作用后，固化土变形较大，经历8次冻融后基本趋于稳定。这是因为未冻融前，土体结构未发生破坏。几次冻融循环使得土中水冻结膨胀、融化迁移，土体内部出现裂缝，土颗粒重新排列组合，进而导致土骨架失稳，土体结构开始破坏。经历8次冻融循环后结构性完全破坏，应力趋于新平衡，达到稳定状态。

图3 σd-εd曲线Fig.3 σd-εd curves

随着冻结温度的降低，固化土动应变相差不大。特别是冻结温度为-15 ℃和-20 ℃时，动应力-应变曲线几乎重合。这说明冻结温度对固化土变形的影响十分有限，冻融次数是影响固化土变形的主要因素。

2.2 冻融作用对动强度的影响

动强度定义为在一定的振动次数（Nf）下，土体产生一 定的允许动应变所需的动应力。在土力学中，剪切强度为试样在45°剪切面上的剪应力τd=σd/2，因而土体的动强度曲线可表示为σd/2-Nf曲线。根据动三轴试验结果，取允许应变为1%[16]，得到动强度曲线，即σd/2-Nf关系曲线，见图4。由图4可知，固化土动强度随着冻融次数的增大而降低。前4次冻融循环作用后，动强度减小较大， 比n=0时降低了21 %～25 %。当n≥8以后动强度逐渐趋于稳定，动强度由200 kPa降低到140 kPa左右，比n=0时减小了27 %～30 %。这说明未经历冻融循环的固化土有较强的结构性，土体动强度较高，随着几次冻融循环后土体内部发生变化，土颗粒间排列和联结发生改变，颗粒间作用力逐渐减小，土体结构性变弱，动强度下降幅度较大。当n≥8后，土体结构完全破坏，并趋于一个新平衡，动强度趋于稳定。

图4 动强度曲线Fig.4 Dynamic strength curves

图5为污泥固化轻质土的峰值强度随冻融次数n变化的关系曲线。峰值强度为偏应力，即轴向应力与径向应力之差（σ1-σ3）。由图5可知，冻结温度越低，峰值强度越小。但随着冻融次数的增加，动强度减小，且最终趋于一点。这说明冻结温度会影响固化土动强度，但随着冻融次数的增加，冻结温度对固化土动强度的影响会减弱。冻融次数是影响污泥固化轻质土动强度的主要因素。

图5 峰值强度与冻融次数n的关系曲线Fig.5 Relationship between the peak strength and freeze-thaw times n

2.3 冻融作用对动初始弹性模量的影响

初始弹性模量：在应力-应变曲线上相当于应力接近于零时的弹性模量，即通过应力-应变曲线起始点所作切线的斜率。由动应力-应变曲线换算后得到Ed-εd曲线，如图6所示。由图6可知，与动强度变化规律类似，初始弹性模量Ed损失量随着冻融次数n的增加逐渐减小，n≥8时，曲线几乎重合。这是由于在几次冻结和融化过程中，土体结构发生变化且骨架重组，土颗粒间排列发生变化，进而导致土颗粒间接触面减少，摩擦力和咬合力降低。随着冻融次数的增加，土体结构趋于新的平衡状态。

图6 Ed-εd曲线Fig.6 Ed-εd curves

冻结温度越低，首次冻融后的Ed损失量越大。T=-15 ℃时，首次冻融后Ed损失量相当于之后多次冻融损失量的累积。当冻结温度为-15 ℃和-20 ℃时，首次冻融后Ed损失量相差不大。由于在首次冻融时，冻结和融化的温差越大，在融化初期土体“融胀”现象[17]越明显。“融胀”现象的出现导致冻结温度降低，土体变形加剧。

3 冻融与循环荷载作用下污泥固化轻质土结构特性演化分析

土体结构性是指土颗粒和孔隙的形态、排列特征以及颗粒间联结作用。土体结构性的强弱是导致土强度变化、变形的根本原因。

3.1 固结压力作用下污泥固化轻质土结构性演化分析

土体原有结构一旦被破坏时，强度突然降低和变形量急剧增加的能力，即结构的可变性[18]。由于结构性土具有强的结构可稳性和结构可变性，因此利用扰动、加荷载等方式破坏土结构性，用结构性破坏时的难易程度和破坏后的变形程度，即结构势，来反映土体结构性的强弱，并提出一个一般土体的结构性定量参数——“综合结构势”。将“综合结构势”定义为：

式中：mp——土体在压力p下的综合结构势；

Sr、Ss、S0——污泥固化轻质重塑土、饱和土、固化土在压力p下的应变量；

m1、m2——结构可变性、可稳性；

将污泥固化轻质土、重塑土和饱和土分别进行固结试验，得到3条e-lgp曲线（图7）。由图7可知，随着外压增大，污泥固化轻质土和饱和土的曲线有明显的拐点。在拐点之前，变形慢慢增加。当压力大于拐点对应的固结压力p=200 kPa后，变形迅速增大，说明此时土的结构性开始丧失；重塑土曲线不具有拐点，说明重塑土不具有结构性。对比3条曲线，污泥固化轻质土的变形特性受结构性影响较为明显。

图7 e-lgp曲线Fig.7 e-lgp curves

将固结试验结果代入式（1）（2）中，计算得到结构势参数m1、m2、mp随着压力p的变化曲线（图8）。

由图8可知，m1随着压力的增大呈下降趋势，说明在压力作用下土颗粒排列受到影响，产生一定的变形， 随着压力增大，下降趋势加快。当压力p为200 kPa（即为e-lgp曲线中，固化轻质土曲线拐点所对应的的压力p）时，S0增大，m2增大，说明此时土颗粒间联结开始破坏，固化土结构性开始丧失。压力继续增大，m2加速增长，说明此时土结构中的联结多数已被破坏。

图8 m1、m2、mp随压力p变化曲线Fig.8 Changes of m1, m2 and mp with pressure p

随着压力的增加，mp先增大后迅速减小，存在峰值点。这是由于较小的压力会挤压固结土颗粒使土颗粒间的摩擦力增加，使得m2减小，mp增大。此时，较小的压力对土体结构有一定的增强作用。之后压力继续增大，导致固结土中联结破坏，土颗粒间发生移动，m2迅速增加，mp迅速降低，结构性加速丧失。

3.2 冻融与循环荷载作用下污泥固化轻质土结构特性分析

郑勋等[19]在“综合结构势”的基础上，提出建立一个既能考虑冻融循环扰动的影响、又能反映结构性随扰动程度不断增加的演化规律的定量参数——冻融结构势：

式中：mpn——冻融作用下固化土在压力p下的冻融结构势；

Sn——冻融作用下固化土在压力p下的应变量。

为研究冻融与循环荷载双重作用下污泥固化轻质土结构特性，在冻融结构势的基础上，提出基于重塑土、饱和土和固化土动应力-应变关系的结构性参数mdσn：

式中：mdσn——冻融与循环荷载作用下污泥固化轻质土的冻融结构势，下标dσn为土体产生一定应变所需的动应力；

σdn、σds、σdr——冻融与循环荷载作用下固化土、饱和土、重塑土相同动应变所需的动应力。

冻融与循环荷载作用下固化土结构性参数mdσn与动应变εd关系曲线见图9。由图9可知，曲线存在峰值点。这是因为荷载小于结构的峰值强度时，土体处于弹性变形阶段，有较小的变形。较小的外力能够增强土颗粒间的咬合力和摩擦力，使得土体结构性有所增强。但随着荷载的增大，土颗粒间的联结被破坏，土颗粒间发生移动，进而导致土体内部结构开始破坏。当荷载进一步加大时，结构完全破坏，土体内部又趋于一个新平衡，mpn变化不大。宏观表现为随着循环荷载的增加，土体内部结构先被加固，产生较小的变形，随后土体结构发生破坏，变形迅速加大。而动弹性模量先迅速减小后趋于平缓，动强度下降。

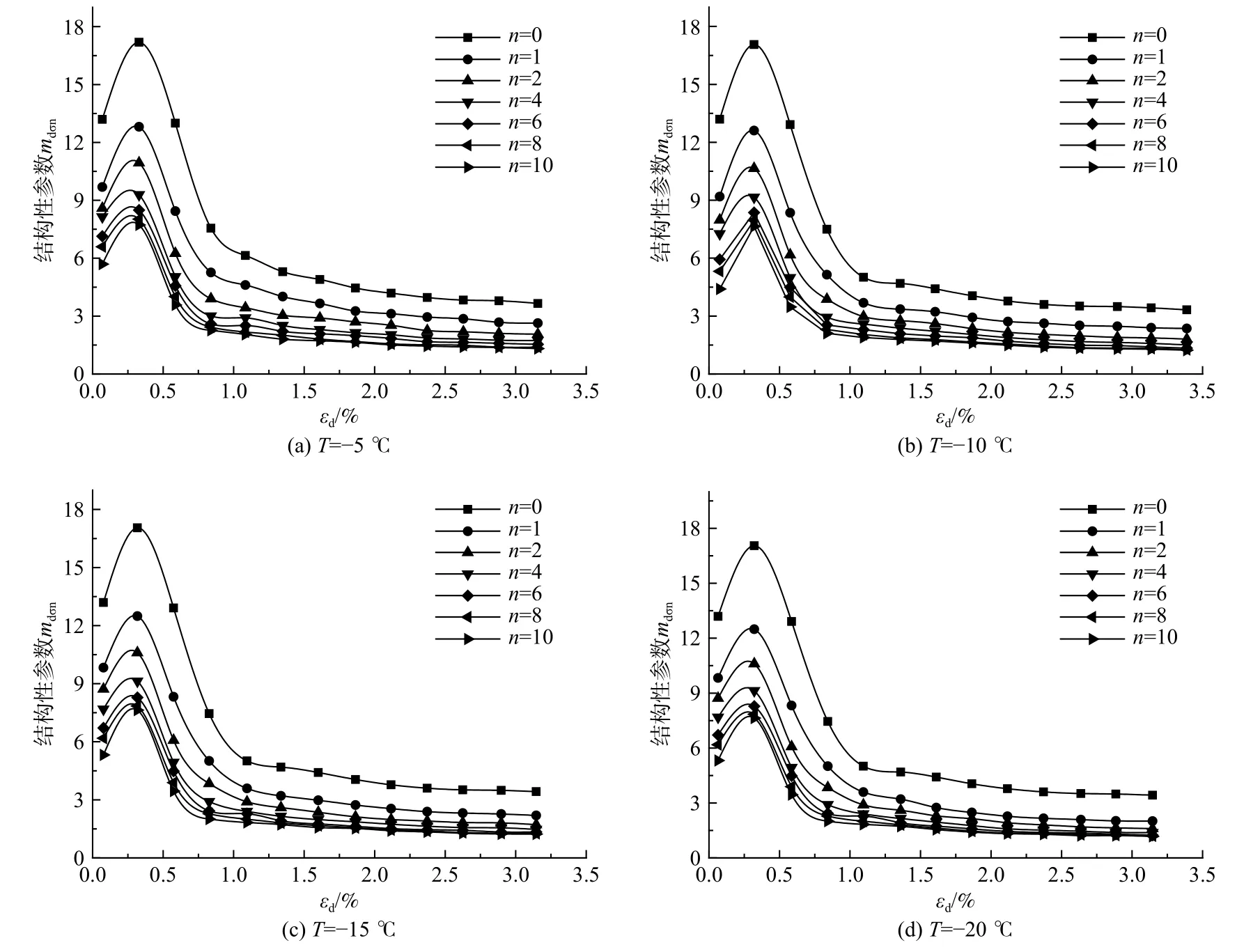
图9 不同冻融循环作用下mdσn-εd曲线Fig.9 mdσn-εd curves under different freezing-thawing cycles

随着冻融次数的增加，mpn损失量增大后趋于稳定。当n≤4时，mpn减小量较大。n≥8时，mpn减小量基本不变。随着冻结温度的降低，mpn有所降低，但下降幅度并不大。从宏观角度来说，冻结温度降低，土体结构性降低，进而导致土体变形，动强度降低。而冻结温度低于-15 ℃时，结构性有所降低，但十分有限，变形和动强度变化不明显。说明固化土结构性是影响土体变形和动强度变化的根本原因。

4 结论

（1）污泥固化轻质土动强度随着冻融循环次数的增加和冻结温度的降低而减小。前4次冻融循环作用后，动强度减小较大。当n≥8时，动强度逐渐趋于稳定。冻结温度对土体动强度的影响较小。

（2）随着冻融次数的增加，动应变增大。前4次冻融作用后，固化轻质土变形较大，经历8次冻融循环后基本趋于稳定。随着n的增加，Ed损失量逐渐减小，n≥8时，曲线几乎重合。随着冻结温度越低，首次冻融后的Ed损失量越大。当冻结温度低于-15 ℃时，Ed损失量相差不大。

（3）当εd＜0.3 %时，结构性参数mdσn增大，达到峰值。当εd＞0.3 %时，mdσn先迅速减小后趋于稳定。当n≤4时，mdσn减小量较大。n≥8时，曲线几乎重合。随着冻结温度的降低，mdσn有所降低，但下降幅度并不大。