海洋湍流对光子轨道角动量量子通信的影响
刘瑞熙 马磊
(成都理工大学地球物理与空间科学系,成都 070801)
本文研究了基于光子轨道角动量的量子通信在水下量子信道中受海洋湍流运动的影响.基于Elamassie等提出的海洋湍流功率谱模型,本文建立了不同海洋湍流参数与光子轨道角动量量子通信的单光子探测概率、信道容量、密钥产生率以及双光子共生纠缠度的定量关系,并利用纠缠光子对的共生纠缠度在海洋湍流中的普适衰减特性进一步研究了轨道角动量纠缠光子对在海洋湍流中的最大纠缠距离.研究结果表明:水下量子通信性能和纠缠光子对的共生纠缠度都随海洋湍流的湍流动能耗散率的增大或温度方差耗散率的减小而降低;温度和盐度因素对海洋湍流贡献的比值对水下量子通信的影响在海水是否稳定分层的条件下具有显著的区别;在通过海洋湍流进行量子通信时,增加信号光子的初始轨道角动量量子数可以提高量子密钥分发的密钥产生率和纠缠光子的纠缠衰减抵抗性.
1 引言
量子通信是一种应用量子叠加态和量子纠缠等量子特性进行信息传输的通信方式,与传统通信技术相比,其最大的优势是由量子力学原理保证的安全性.2010年,潘建伟团队[1]实现了16 km 的量子隐形传态实验,首次证实了在自由空间进行远距离量子态隐形传输的可行性.2017年,金贤敏团队[2]完成了基于海水信道的量子通信实验,首次验证了水下量子通信的可行性,对进一步开拓包括水下量子信道在内的全球化量子通信系统具有重要意义.量子信号在传输过程中会不可避免地受到外界环境因素的影响导致量子退相干,使得量子通信性能下降甚至中断.在自由大气中进行量子通信时,光子的传输会受到天气、空气污染等自然环境因素的影响.聂敏等[3-6]对基于单光子传输的量子通信性能在降雨[3]、降雪[4]、沙尘暴[5]和大气污染[6]等具体自然环境因素影响下的衰减做了大量的研究.与自由空间量子通信类似,水下量子通信的性能也会受到海水的吸收、散射和复杂的湍流运动等环境因素的影响.嵇玲等[2]进行了室内海水管道中的偏振光子传输实验,发现光子的偏振特性在通过海水通道时能够得到保持.已有的理论和实验研究表明,在海水通道的吸收和散射作用的影响下利用偏振光子进行短距离的水下量子密钥分发是可行的[7,8].
涡旋光束可以携带具有任意整数形式的量子数l=0,±1,±2···的轨道角动量光子(Orbital-angularmomentum photons,OAM 光子)进行量子态传输[9].不同于偏振光子只能用于编码二维量子信息,OAM 光子可以运用任意数量的特征态编码高维度的量子信息[10],同时确保更高的信道容量[11,12]并增强量子通信信道的安全性[13].此外,由于OAM态在传输方向上具有旋转不变性,采用OAM 编码可以避免通信双方对参考系的实时校准[14].然而当涡旋光束在湍流介质中传播时,由于介质折射率的随机波动,涡旋光束的波前相位结构将会遭到破坏而产生相位畸变,造成OAM 信号光子的丢失.对于自由空间中的OAM 量子通信,国内外学者就大气湍流影响下的OAM 单光子以及纠缠 OAM光子对的传输开展了大量研究.Paterson[15]推导了OAM 光子在大气湍流影响下的探测概率公式,并且从理论上分析了大气湍流对量子信道容量的影响;Ibrahim 等[16]通过数值和实验研究了纠缠OAM 单光子和双光子在大气湍流中的纠缠衰减,证明了量子纠缠态在大气湍流中随着OAM 量子数的增加而变得更加稳定.
对于水下OAM 量子通信,Bouchard 等[17]完成了基于光子轨道角动量的水下量子通信实验,并对水下量子信道中不同的量子密码协议进行比较,证明了水下高维编码方案的可行性;胡涛等[18]基于Nikishov 提出的海水折射率功率谱模型,计算了拉盖尔-高斯(Laguerre-Gaussian,LG)光束在不同水下湍流因素和不同传输距离条件下的OAM量子信道容量;Cheng 等[19]用Rytov 近似理论给出了海洋湍流因素对轨道角动量螺旋谱的影响,结果表明不同模式的OAM 信号光子在海洋湍流作用下会发生串扰;Elamassie 等[20]提出了新的海洋湍流功率谱模型,考虑了海水分层的不稳定性以及温度与盐度的涡流扩散率的差异,为研究更接近真实海洋环境下的海洋湍流运动特性奠定了基础.目前,国内外学者针对海洋湍流对OAM 量子通信性能的影响的研究基于简单地假设海水稳定分层的Nikishov 海洋湍流模型,而采用Elamassie 海洋湍流模型能够反映OAM 光子在更复杂的海洋湍流中的传输情况.此外,研究海洋湍流中的光子纠缠特性对于提高水下量子通信性能具有重要意义,然而对于纠缠OAM 光子对在海洋湍流背景下的纠缠衰减特性的研究还未见报道.
本文基于Elamassie 等提出的海洋湍流功率谱模型,针对LG 光束在海洋湍流中传播的波前相位畸变所导致的OAM 量子态串扰,通过分别计算不同海洋湍流参数下的OAM 单光子探测率、信道容量、密钥产生率和纠缠OAM 光子对的共生纠缠度,分析研究了OAM 量子通信性能以及纠缠OAM光子对的纠缠特性在海水量子信道中受各海洋湍流因素的影响,并且提出了纠缠OAM 光子在海洋湍流中的最大纠缠距离与各海洋湍流参数的关系,为进一步研究基于光子轨道角动量的水下高维量子通信系统提供了理论依据.
2 理论模型
Elamassie 等[20]基于Nikishov 提出的海水折射率功率谱模型,考虑了温度和盐度的涡旋扩散率彼此不同而导致海水分层的不稳定,提出了更符合实际海洋环境的海洋湍流功率谱模型,即
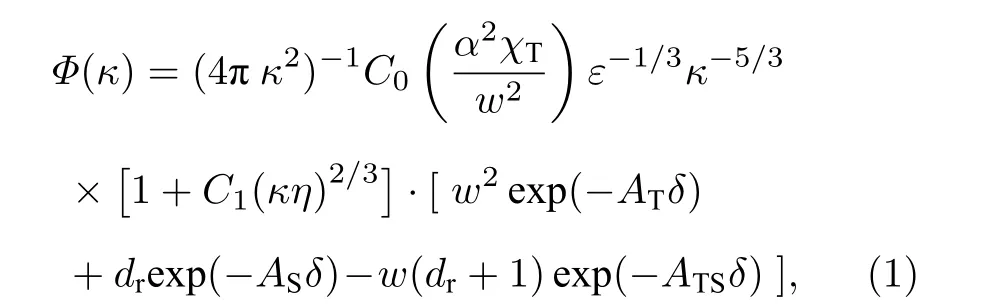
式中:κ是海洋湍流功率谱空间波数;η是Kolmogorov 内尺度;χT是温度方差耗散率,χT∈[10-4,10-10]K2·s-1;ε是湍流 动能耗散率,ε ∈[10-1,10-10]m2·s-3;w∈[-5,0]是温度和盐度对折射率变化贡献的比率,当其取值为—5 和0 时分别代表由温度和盐度起伏引起的海洋湍流;温度因子为AT=1.863×10-2,盐度因子为AS=1.9×10-4,综合影 响因子ATS=9.41×10-3,中间变量为δ=8.284(κη)4/3+12.978(κη)2;α是热膨 胀系数;常数C0=0.72,C1=2.35 ;dr为涡流扩散率,当海水稳定分层时,dr取值为1,当海水不稳定分层时,dr表达式为关于w的分段函数[20]

在Rytov 近似下,各向同性海水介质中球面波的波结构函数为[21]
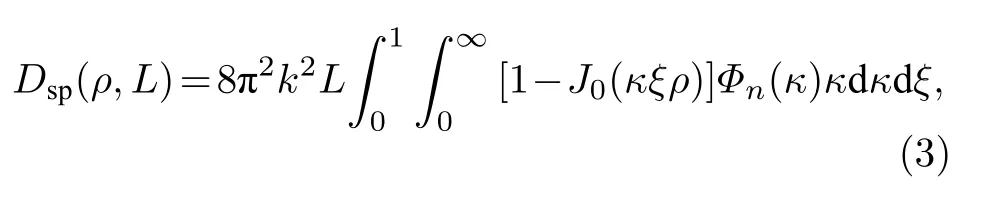
其中ρ为光束波阵面上两点间距,L为传播距离,ξ=1-z/L为归一化距离变量,z是可变距离.由此可以推导出在惯性范围内即(ρ≫η)的海洋湍流中球面波的波结构函数的解析表达式为[22]
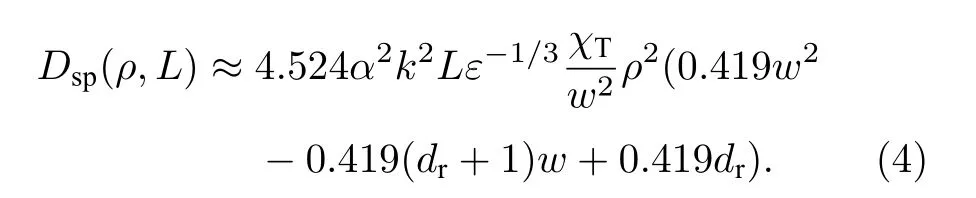
根据空间相干长度ρ0的定义式D(ρ0,L)=2,得到海洋湍流中球面波的空间相干长度为
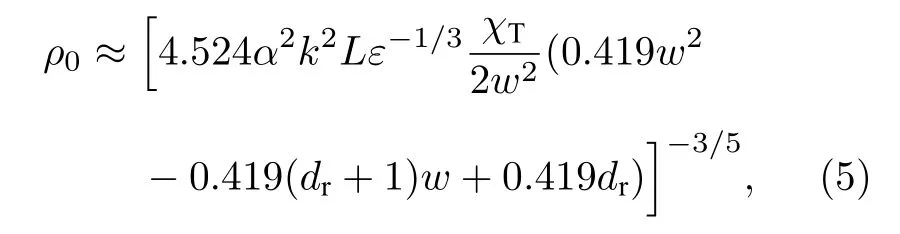
由(4)式、(5)式可以得到
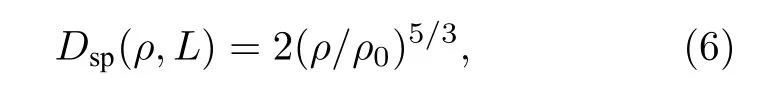
由Fried 参数的定义[23]可得海洋湍流中的球面波Fried 参数r0的表达式
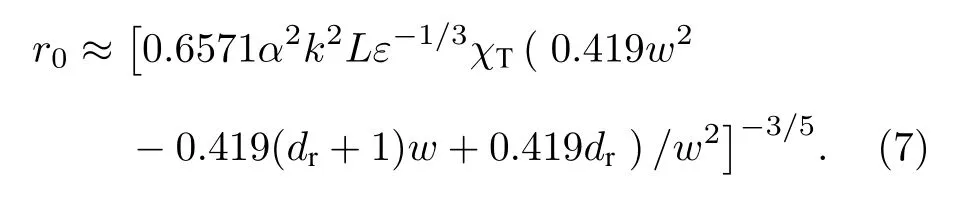
引入Fried 参数r0,再由(5)式、(6)式可得到由海洋湍流导致涡旋光束波前相位畸变的相位结构函数表达式为

(8)式表明基于Elamassie 海洋湍流功率谱得到的在惯性范围内的海洋湍流中传播的球面波相位结构函数仍满足大气湍流中的Kolmogorov 三分之五幂律.
3 数值仿真
3.1 海洋湍流对OAM 单光子探测率的影响
根据LG 光束在湍流中传播的Rytov 近似理论,可以设初始OAM 量子数为l0,径向量子数为p0的LG 光束在湍流中传播距离z处的波函数复振幅为

其中,LG 光束的径向分量Rl0,p0(r,z)的表达式为[24]

定义半径为r处的相位畸变的旋转场相干函数为

其中,Dϕ(r)是海洋湍流中的球面波相位结构函数.
由此得到OAM 量子数为l的光子的探测概率[15]为
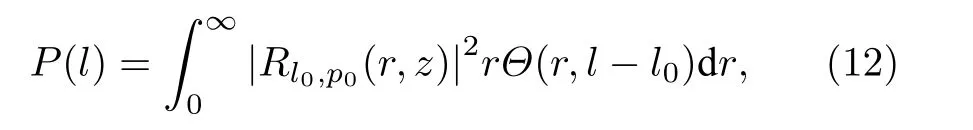
式中,Θ(r,l-l0) 是旋转相干函数的圆谐波变换,其表达式为

下面根据(2)式、(6)式、(8)式和(12)式,对初 始OAM 量子数l0=1,径向量子数p0=0的OAM 单光子探测概率与不同海洋湍流因素的关系进行仿真.
图1(a)分别给出了dr=1和对应的两种海洋湍流功率谱模型下的单光子探测概率随温度-盐度贡献比变化的曲线.计算参数为λ=417 nm,ω0=0.01 m,z=10 m,α=2.6×10-41/deg,ε=10-5m2/s3,χT=10-7K2/s.从图1(a)可以看出:当dr=1时,对应于海水稳定分层的情况,单光子探测概率随温度-盐度贡献比的绝对值|w|的减小而单调递减,由盐度因素主导的湍流对单光子传输的影响更加显著.当时,对应于海水不稳定分层的情况,在1<|w|≤5的范围内,单光子探测概率随温度-盐度贡献比的绝对值|w|的减小而降低并且始终满足,表明海水不稳定分层时的海洋湍流对单光子探测的干扰更加显著;值得注意的是在|w|=1时,满足,此时两种情况下的海洋湍流对单光子探测的干扰相等;而在0.5 ≤|w|≤1的范围内,随|w|减小而逐渐增大,并在|w|=0.5处取得最大值之后随|w|减小而讯速降低;以上结果表明海水是否稳定分层对单光子探测概率的影响具有较大的差异.

图1 单光子探测概率与w 的关系Fig.1.Relationship between single photon detection probability and w.
图2 给出了单光子探测概率随湍流动能耗散率χT和温度方差耗散率ε变化的关系.计算参数为λ=417 nm,ω0=0.01 m,z=10 m,α=2.6×10-41/deg,w=-5,dr=1.可以看出:当湍流动能耗散率χT增大或温度方差耗散率ε减小时,海洋湍流随之增强,导致单光子探测概率降低.

图2 单光子探测概率与 χ T 和ε 的关系Fig.2.The relationship between single photon detection probability and χ T and ε.
3.2 海洋湍流对OAM 量子信道容量的影响
信道容量可以通过单光子探测概率量化,从而评价海洋湍流对通信链路的影响,信道容量的定义为
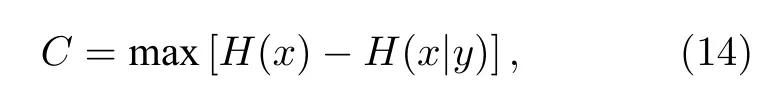
其中,H(x)是信号原始信息的熵,H(x|y)给定接收信息为y 时的条件熵,二者分别定义为[15]

式中,P(xi) 是传输信号为{xi}的概率,P(yj|xi)是给定发射信号为{xi}的条件下所接受到的信号为{yj}的条件概率.假设信道中传输的LG 光束具有OAM 量子数的范围为l0=-L0,···,L0,则每种信号的概率为Pxi=1/(2L0+1),信号源的熵为H(x)=log(2L0+1).经过海洋湍流传输后,探测器接收到具有不同OAM 量子数的光子的概率可以通过(12)式得到.
下面通过对不同初始OAM 量子数范围的LG光束在不同程度的海洋湍流环境中的信道容量进行数值计算,研究在不同海洋湍流环境下的OAM量子信道衰减特性.
图3 为不同初始OAM 量子数范围的LG 光束在海洋湍流背景下的信道容量随不同海洋湍流参数的变化曲线.计算参数分别为λ=417 nm,ω0=0.01 m,α=2.6×10-41/deg.由 图3(a)、图3(b)可知:信道容量随湍流动能耗散率χT增大或温度方差耗散率ε减小而不断衰减;图3(c)表明:随着传输距离的增加,信道容量迅速衰减;图3(d)表明:温度-盐度贡献比对信道衰减的影响与对单光子探测概率的影响在变化趋势上是相似的,即在海水是否稳定分层的条件下具有显著的差异.以上结果表明:在海洋湍流强度相同的条件下,初始OAM量子数范围越大的LG 光束具有数量更多的量子编码态,其对应的信道容量就越大.
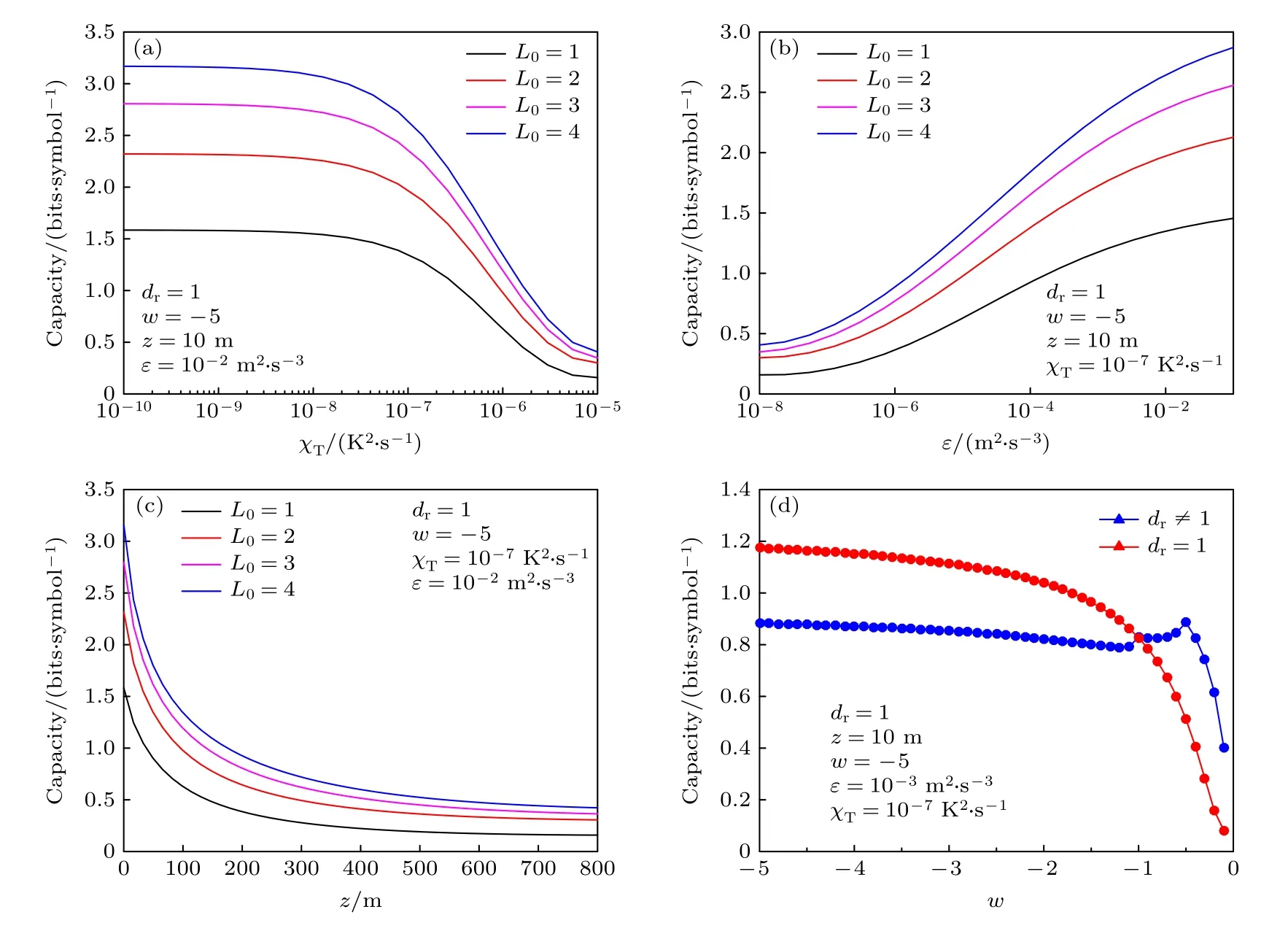
图3 信道容量随各海洋湍流参数的变化关系Fig.3.The relationship of channel capacity with the ocean turbulence parameters.
3.3 海洋湍流对OAM 量子密钥分发的密钥产生率的影响
基于Lo 等[25]提出的测量设备无关量子密钥分发(measurement-device-independent quantum key distribution,MDI-QKD)协议的OAM 量子密钥分发系统,其安全密钥产生率的计算公式为[26]

式中,µ、υ分别为Alice、Bob 每次脉冲发射的平均光子数;为在OAM 基下发射单光子的计数率;为叠加基下的单光子误码率;是平均光子数分别为µ、υ时的总接收率(总误码率);f为纠错效率;H(x)为二元香农熵函数.
采用Wang 等[26]提出的方法计算,设为接收光子与发射光子具有相同(不同)OAM 状态的概率,η0和可以利用(12)式计算得到,即密钥分发系统的仿真参数值如表1 所列,其中Pd为探测器的暗计数率,ed为基未对准概率.
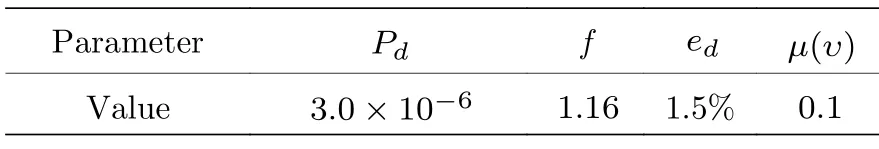
表1 密钥分发系统的仿真参数值Table 1.Simulation parameters of key distribution system.
图4 给出了不同初始OAM 量子数下的密钥产生率随传输距离的变化关系.计算参数为λ=417 nm,ω0=0.01 m,α=2.6×10-41/deg,w=-5,dr=1,χT=10-7K2·s-1,ε=10-5m2·s-3.结果表明:在海洋湍流的影响下,量子密钥分发系统的密钥产生率随传输距离的增加而迅速减小;OAM 编码光子的最大传输距离随初始OAM 量子数的增大而增加.
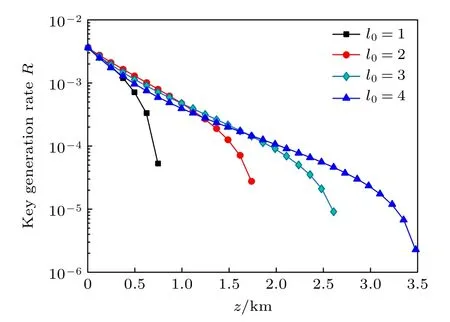
图4 密钥产生率随传输距离的变化关系Fig.4.The relationship of key generation rate with transmission distance.
3.4 海洋湍流对OAM 光子对纠缠衰减的影响
下面考虑一对由束腰半径为ω0的LG 光束传输的纠缠光子,它们具有相同的径向量子数p0=0,以及相反的OAM 量子数l0和-l0.设初始状态下的纠缠光子处于可以通过实验制备的Bell 态[27],定义为
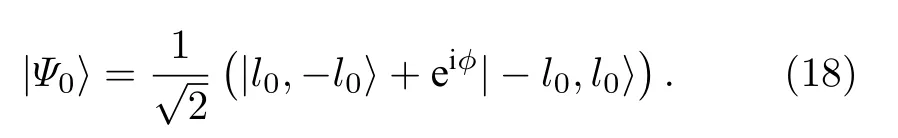
若仅考虑海洋湍流对LG 光束的相位畸变效应,则纠缠光子穿过的海洋湍流层可以等效为一个随机相位屏.将海洋湍流对光子的作用视为一个线性算符Λ,则探测器接收到光子的量子态表示为[28]
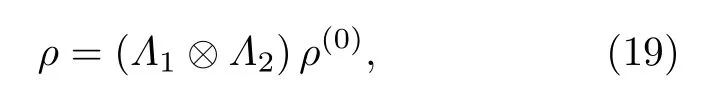
其中,Λ1和Λ2分别表示这两个光子所处信道中的海洋湍流对光子的作用.假设海洋湍流对两个光子的相位干扰具有相同的统计特性,则有Λ1=Λ2=Λ.算符Λ的矩阵元表示为
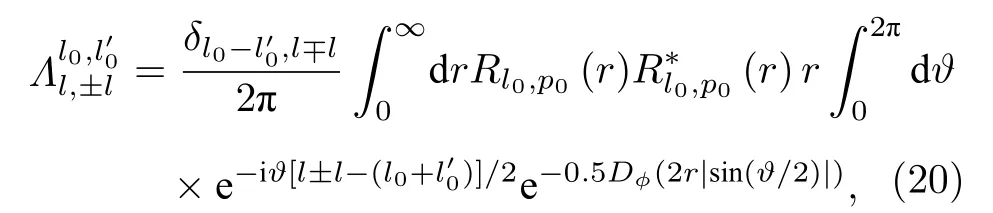
定义初始量子态的基矢为{|l0,l0〉,|l0,-l0〉,|-l0,l0〉,|-l0,-l0〉},根据Wootters 提出的双量子混合态的共生纠缠度公式[29],可以得到输出量子态共生纠缠度的解析表达式为
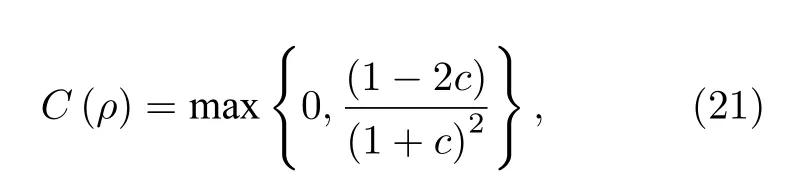
其中,c=b/a,a和b分别定义为OAM 光子信号的生存振幅和串扰振幅

下面根据(20)—(23)式,对初始OAM 量子数l0=1,径向量子数p0=0的OAM 双光子共生纠缠度与不同海洋湍流因素的关系进行仿真.
图5 给出了共生纠缠度随湍流动能耗散率χT和温度方差耗散率ε变化的关系.计算参数为λ=417 nm,ω0=0.01 m,z=1000 m,α=2.6×10-41/deg,dr=1.由图5 可知:共生纠缠度随湍流动能耗散率χT增大或温度方差耗散率ε减小而降低,对应于海洋湍流随湍流动能耗散率χT增大或温度方差耗散率ε减小而增强,导致信号光子的串扰振幅增大直至纠缠完全消失,即纠缠猝死现象[30].
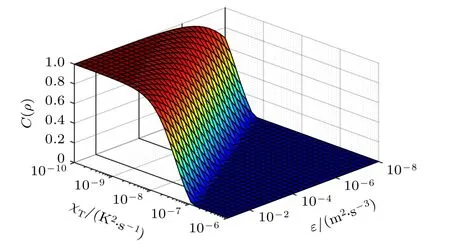
图5 共生纠缠度与 χ T 和ε 的关系Fig.5.The relationship between output state concurrence and χ T and ε.
图6 给出了共生纠缠度随传播距离z和温度-盐度贡献比w变化的关系.计算参数分别为λ=417 nm,ω0=0.01 m,χT=10-7K2·s-1,ε=10-5m2·s-3,α=2.6×10-41/deg,dr=1.由图6可知:在相同传播距离的条件下,共生纠缠度随温度-盐度贡献比的增大而降低,表明由盐度起伏引起的湍流对共生纠缠度的影响更加显著.
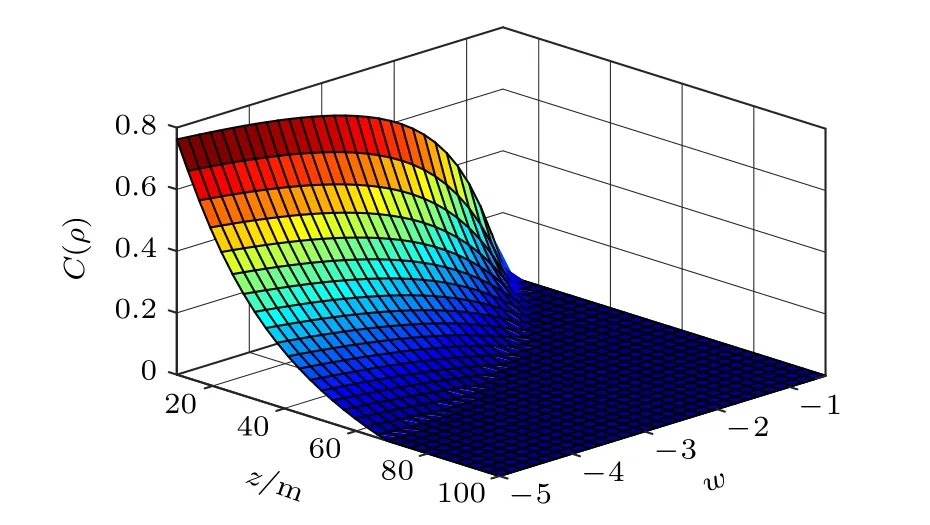
图6 共生纠缠度与z 和w 的关系Fig.6.The relationship between output state concurrence and z and w.
为了探究不同初始OAM 量子数的纠缠光子在海洋湍流中的纠缠衰减特性,在应用Fried 参数r0表征的特定湍流强度下,计算了不同初始OAM量子数l0的共生纠缠度衰减曲线,结果如图7 所示.计算参数为λ=417 nm,ω0=0.01 m,χT=10-7K2·s-1,ε=10-5m2·s-3,α=2.6×10-41/deg,dr=1.由图7 可知:在海洋湍流强度相同且纠缠未完全消失的条件下,初始量子数l0越大则共生纠缠度越高,表明具有更高初始OAM 量子数的纠缠光子对在湍流中的纠缠衰减更缓慢.

图7 共生纠缠度与 l0 和 r0 的关系Fig.7.The relationship between output state concurrence and l0 and r0.
为了研究不同初始OAM 量子数的纠缠光子对的共生纠缠度在海洋湍流中的普适衰减特性,按照文献[28]中的方法引入相位相干长度,定义为
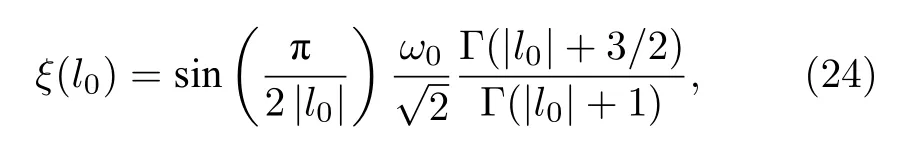
其中,ω0为LG 光束的束腰半径,Γ (x)为伽玛函数.
对共生纠缠度C(ρ)、相位相干长度与Fried参数的特征比值x=ξ(l0)/r0之间的关系进行仿真,结果如图8 所示.
图8 给出了不同初始OAM 量子数l0的纠缠光子对应的共生纠缠度衰减曲线.当r0≫ξ(l0)时,海洋湍流对双光子态的共生纠缠度几乎没有影响,随着r0逐渐趋近于ξ(l0),海洋湍流对光波波前的相位扰动效果增强,导致不同量子态之间的串扰加剧,从而使共生纠缠度快速衰减至0.此外,不同初始OAM 量子数l0>1的纠缠光子的纠缠衰减与一条指数型函数曲线拟合得很好,由此可以得到不同OAM 量子数l0>1的纠缠光子的普遍纠缠衰减特性,其拟合曲线的表达式为f(x)=exp(-3.54x2.93).为了验证计算结果的可靠性,图8 还画出了Leonhard 等[28]提出的OAM 纠缠光子对在大气湍流中传播的普遍纠缠衰减曲线,其表达式为g(x)=exp(-4.16x3.24),可以看出两条拟合曲线的结果基本一致.

图8 共生纠缠度与 ξ (l0)/r0 的关系Fig.8.The relationship between output state concurrence and ξ (l0)/r0.
3.5 海洋湍流中的最大纠缠距离
为了表征在大气湍流中传输的纠缠光子发生纠缠衰退的空间尺度,Ibrahim 等[16]将退相干距离Ldec被定义为共生纠缠度衰减至0.5 所对应的传播距离,并且退相干距离与量子数满足关系Ldec∝(l0)5/6.纠缠光子对在海洋湍流中的共生纠缠度随特征比值ξ(l0)/r0的衰减规律对于不同量子数的纠缠光子具有普适性,因此可以将特征比值ξ(l0)/r0作为判断纠缠衰减程度的依据.定义共生纠缠度衰减至0 所对应的传输距离为最大纠缠距离,将ξ(l0)/r0=1作为纠缠完全消失的判别依据,根据(6)式、(8)式、(20)式、(21)式可以得到海洋湍流中的最大纠缠距离的表达式:
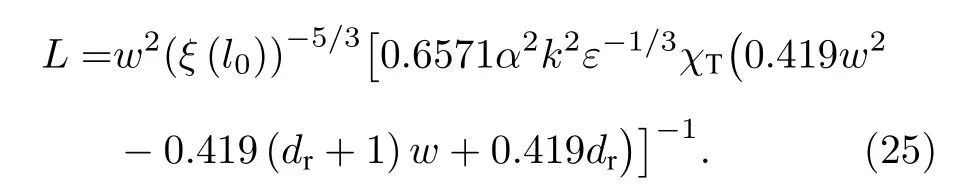
下面根据(24)式、(25)式,对不同初始OAM量子数的纠缠光子在海洋中的最大纠缠距离与各海洋湍流因素的关系进行仿真.
图9 为不同初始OAM 量子数的纠缠光子对在海洋湍流背景下的最大纠缠距离随不同海洋湍流因素的变化曲线.计算参数分别为λ=417 nm,ω0=0.01 m,α=2.6×10-41/deg.由 图9(a)、图9(b)可知:最大纠缠距离随湍流动能耗散率χT增大或温度方差耗散率ε减小而迅速降低;图9(c)表明:温度-盐度贡献比对最大纠缠距离衰减的影响在海水是否稳定分层的条件下具有显著的区别,与图1(a)中的不同海洋湍流模型下的单光子探测概率随温度-盐度贡献比变化的曲线具有相似的变化趋势;图9(d)给出了最大纠缠距离与初始OAM 量子数的关系:在海洋湍流强度相同的条件下,初始OAM量子数越大则对应的最大纠缠距离越远,并且最大纠缠距离与初始OAM 量子数满足关系L∝(l0)5/6,图中给出的拟合曲线表达式 为L(l0)=62.2l05/6,与Ibrahim 等[16]定义的大气湍流中的退相干距离Ldec随l0变化的指数关系一致.
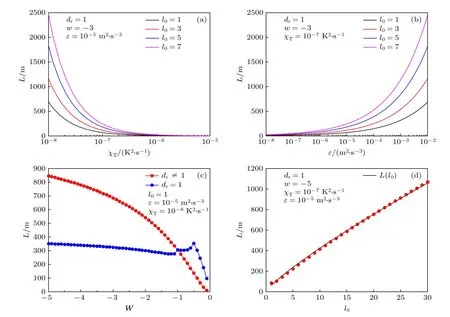
图9 共生纠缠度随各海洋湍流参数的变化关系Fig.9.The relationship between concurrence and the ocean turbulence parameters.
4 结论
本文基于Elamassie 海洋湍流功率谱模型,建立了OAM 单光子探测概率、信道容量、密钥生成率和纠缠OAM 光子对的共生纠缠度与各海洋湍流参数之间的定量关系,研究了海洋湍流运动对基于光子轨道角动量的水下量子通信性能和纠缠特性的影响.仿真结果表明:当湍流动能耗散率χT增大或温度方差耗散率ε减小时,海洋湍流随之增强,引起OAM 信号光子在不同模式之间的串扰加剧,从而导致OAM 量子通信的信道容量、密钥产生率和纠缠光子对共生纠缠度的降低;对于Nikishov海洋湍流功率谱,信道容量、密钥生成率和纠缠光子对共生纠缠度随温度-盐度贡献比的绝对值|w|的减小而单调递减,由盐度因素主导的湍流对水下量子通信的干扰更加显著;而Elamassie 提出的海洋湍流功率谱考虑了更合理的海水不稳定分层的情况,即涡流扩散率dr的取值不再恒等于1 而是随温度-盐度贡献比w变化,因此温度-盐度贡献比w对水下量子通信性能和纠缠特性的影响在海水是否稳定分层的条件下具有显著的区别;在海洋湍流强度相同的条件下,初始OAM 量子数l0越大则对应的最大密钥分发距离和最大光子对纠缠距离越远.因此,在进行基于光子轨道角动量的水下量子通信时,可根据实际情况适当提高信号光子的初始OAM 量子数以降低海洋湍流对量子通信的影响.本文的研究结果对于海洋湍流环境下的某些实用性的量子密码协议,如量子保密查询[31]等,也具有重要的参考价值.

