基于改进Henon映射和超混沌的双重语音加密算法
张秋余,宋宇杰
基于改进Henon映射和超混沌的双重语音加密算法
张秋余,宋宇杰
(兰州理工大学计算机与通信学院,甘肃 兰州 730050)
针对现有语音混沌加密算法密钥空间小、安全性差、加密效率低且无法实现密钥复杂度与加密效率的权衡等问题,提出了一种改进Henon映射和超混沌的双重语音加密算法。首先,为了使Henon映射具有更大的混沌空间和更高的混沌复杂度,通过扩展控制参数范围将非线性三角函数作为输入参数变量等手段对经典Henon映射进行了改进;其次,利用改进的Henon映射生成伪随机序列,并对语音数据进行单次不重复置乱加密,获得语音数据的初次加密结果;最后,利用Lorenz超混沌系统对初次加密后的语音数据进行Arnold二次置乱加密和异或扩散加密,获得最终的密文语音数据。实验结果表明,与现有方法相比该算法具有更大的密钥空间和更高的加密效率,且对各种密码攻击拥有更好的鲁棒性。
语音加密;改进的Henon映射;Lorenz超混沌系统;Arnold变换;鲁棒性
1 引言
随着云存储、计算机网络的快速发展,多媒体技术已经在人类的日常生活中发挥了重要作用[1]。其中,语音具有表义功能而被广泛关注,如会议录音、法庭证据等,这些应用都体现了语音内容的重要性,如何确保语音数据的安全传输成为研究热点之一。
目前,学者们提出了许多用于保护语音数据的加密方法。常用的加密方法有混沌映射加密[2]、置乱加密、同态加密[3]、AES加密[4]、RSA加密[5]、DES加密[6]等,这些加密方法使加密后的语音数据变得杂乱无章,有效地保护了语音数据免受不法分子的破译和篡改。混沌系统生成的随机序列因其对初值敏感性、密钥不可预测性和良好的统计特征,被广泛地应用于图像、音频、视频等多媒体加密[7]。经典的混沌系统主要包括一维的Logistic映射[8]、二维的Henon映射[9]、三维的Lorenz映射[10]以及基于改进的超混沌系统。但现有低维的混沌映射大多存在周期性短、混沌区间小、复杂度低等问题,无法实现对多媒体数据的安全加密;高维的混沌映射又普遍存在算法复杂度高、加密效率低等问题,无法实现海量多媒体数据的安全存储。因此,学者们对常用的混沌加密算法进行了改进和创新,并取得了众多成果。通常混沌加密算法的改进主要分为两类:一类是通过优化改进适用于语音加密的伪随机序列;另一类是针对加密算法的设计结构改进和创新。
针对第一类语音加密方案中,不少学者在保证不改变系统变量的情况下,对经典的混沌映射进行改进,创建了具有系统复杂度更高的混沌系统用以实现对多媒体数据加密。Sayed等[11]提出一种具有3个独立参数改进的混沌映射,并利用该算法与置换网络实现了语音加密。改进的混沌映射增强了混沌特性,简化了映射方程的取模运算,有效地克服了控制参数范围限制和动态退化问题。Farsana等[12]提出一种基于音频置乱的语音加密方案,该方案在经典Henon映射的基础上对算法进行优化改进,改进后的算法具有更大的混沌区间和更高的系统复杂性,使用改进的Henon映射对语音数据执行置乱操作,结合Lorenz超混沌系统进行替换操作,实现了语音数据高效安全的加密。Hamdi等[13]通过改进Henon映射,增大了混沌参数区间,减小了周期窗口,扩展了密钥空间。为避免长时间使用固定混沌序列作为密钥带来的安全隐患,该方法增加混沌序列的随机性,并利用动态分组加/解密系统良好的保密性,有效防止了基于混沌的模型重构方法带来的攻击,提高了算法的鲁棒性。Zghair等[14]提出一种具有12个正参数的七维三阶非线性超混沌系统,该算法增加了语音的密钥空间,提高了算法的鲁棒性,但高维数的混沌系统增加了算法复杂度,降低了加密效率。
另一类语音加密方案是通过对现有的加密结构设计优化,用以实现更高效安全的多媒体信息加密。如Shah等[15]提出一种新的三维混沌映射的语音加密方案,首先将语音分成8位序列和7位序列,随后对分离的序列用不同高质量的替换盒进行替换,并将替换盒通过伽罗瓦域上Mobius变换生成密文语音,能够抵抗统计攻击和差分攻击,具有较强的鲁棒性。Imran等[16]提出一种非对称密钥语音加密模型,发送方使用生成的公钥对语音加密,接收方使用生成的私钥解密并实现语音重构,具有较高的安全性。Elsafty等[17]提出一种基于动态S-box的语音加密算法,该算法提出S盒中的数据并不是固定不变的,而是利用混沌系统生成的伪随机序列对S盒中的数据进行动态变换,用以实现语音数据加、解密。
综上所述,为了解决现有基于混沌映射的语音加密算法大多存在密钥空间和加密算法复杂度等问题,本文给出了一种基于改进Henon映射和超混沌的双重语音加密算法,该算法在确保语音加密系统拥有较大密钥空间的同时,降低了语音数据的加密时间,增加了算法的鲁棒性,实现了高效安全的语音加密。本文的主要创新工作如下。
(1)为了解决现有混沌系统控制参数多、混沌区间小等问题,通过扩展控制参数范围、将非线性三角函数作为输入参数变量等手段对经典Henon映射进行了改进,增大了混沌序列的伪随机性。
(2)利用改进Henon映射生成的伪随机序列对语音数据实现单次不重复置乱加密,克服了传统随机置乱加密中对单列数据重复置乱的缺点,减少了语音的加密时间,提高了语音加密效率。
(3)为了提高加密算法的密钥空间、鲁棒性和安全性,将改进Henon映射与Lorenz超混沌加密系统相结合,采用改进的广义Arnold置乱算法,实现了语音数据双重加密。
2 预备知识
2.1 改进的Henon混沌系统
经典的Henon映射函数[18]表达式如式(1)所示。
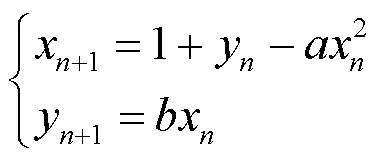
本文改进的Henon混沌映射是在经典的Henon混沌映射的基础上对函数表达式和系统参数进行改进,改进的Henon映射表达式如式(2)所示。
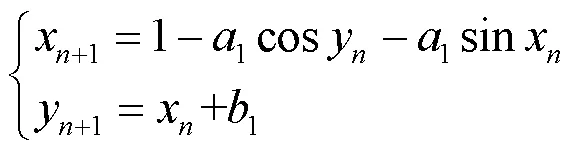
从图3中可以看出,改进的Henon映射相空间图相比于经典的Henon映射相空间图具有更大的混沌区间、更复杂的混沌特性。因此,本文改进的Henon混沌映射具有更大的随机性、低互相关性和遍历性,更适用于语音加密系统。
2.2 Lorenz超混沌系统
Lorenz超混沌系统是在经典Lorenz混沌系统[19]的基础上进行改进和优化[20],并利用附加的状态变量将原始的三维系统改进为四维超混沌系统。本文引用Lorenz超混沌系统,不仅增大了加密算法的密钥空间和伪随机性,同时增加了算法的鲁棒性和安全性。Lorenz超混沌系统函数表达式如式(3)所示。

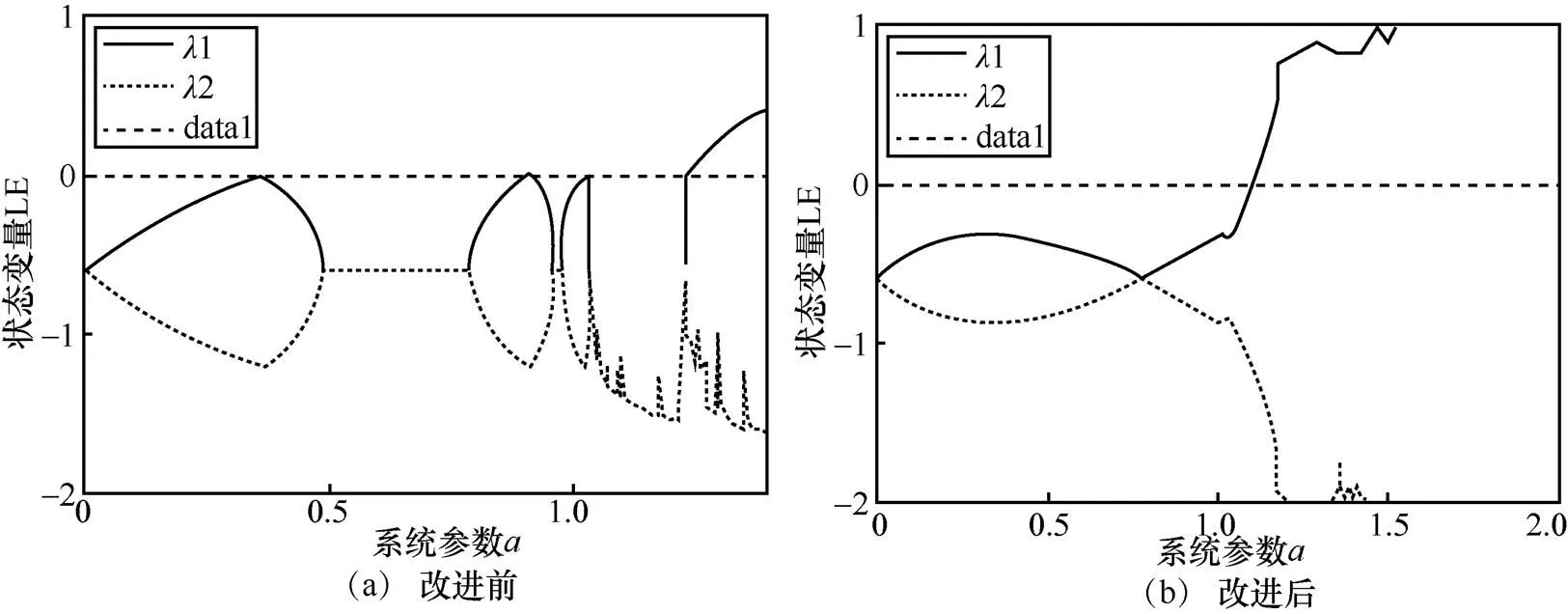
图2 Henon映射改进前后的Lyapunov指数图
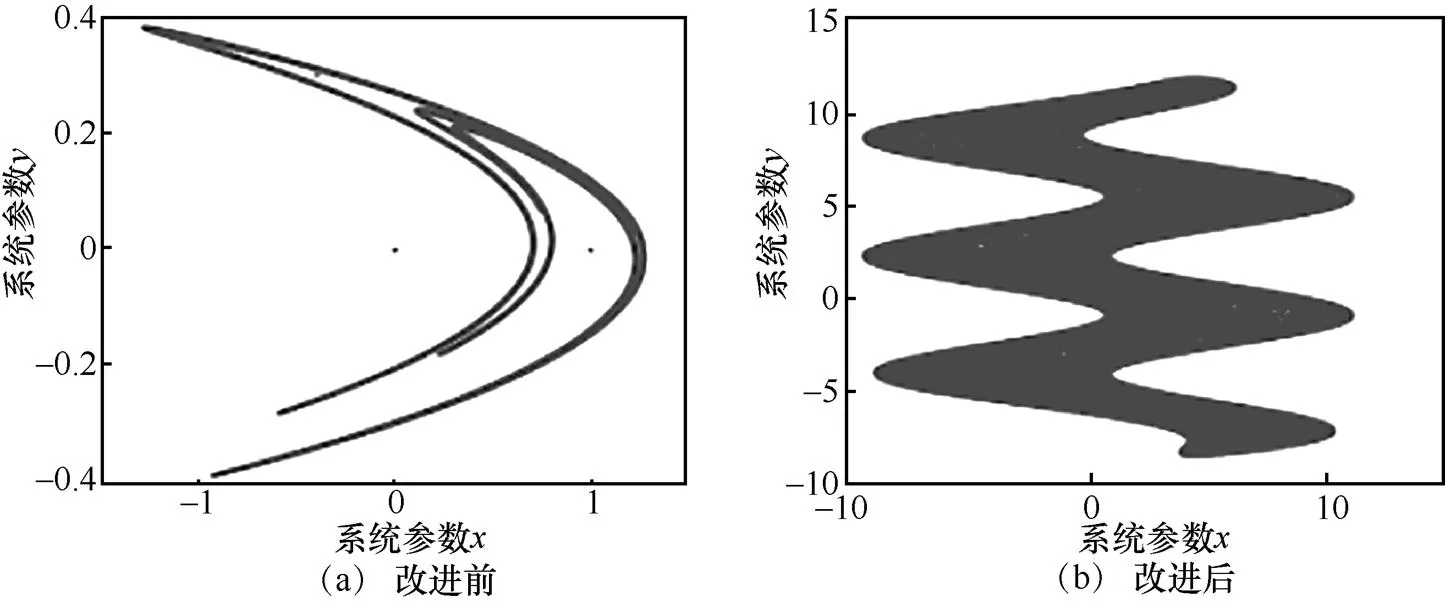
图3 Henon映射改进前后的相空间图
2.3 改进的Arnold变换算法
本文对经典的Arnold变换算法[21]进行优化,将传统的二维矩阵转化为一维向量进行置乱操作。具体方案如下。
(1)经典的二维不等长Arnold置乱算法定义如式(4)所示。
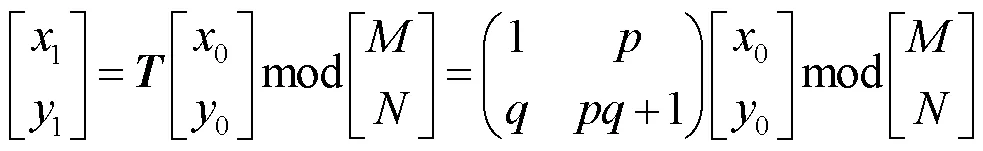
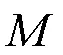
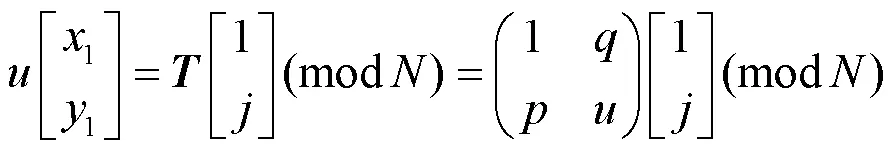
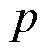
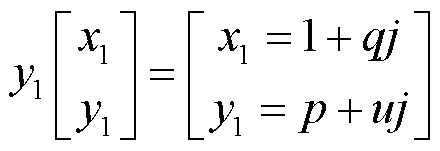
(5)Arnold置乱反变换:在使用伪随机矩阵进行语音置乱加密时,由于置乱算法本身是可逆的,在对数据进行解密时,只需要对Arnold置乱变换的加密数据按语音数据长度进行反向置乱即可恢复原始语音数据。
本文改进的Arnold置乱加密算法相比较于传统的Arnold行列置乱加密算法,有效地克服了传统Arnold置乱加密中存在周期短、安全性差等问题,并且将数据转换为一维向量,有效地减少了加密时间,提高了加密效率。
3 算法设计
3.1 语音初次加密算法
语音初次加密算法处理流程如图4所示,主要包括:语音数据预处理、模数转换、置乱加密、数模转换、密文语音输出等步骤,具体过程如下。
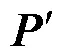
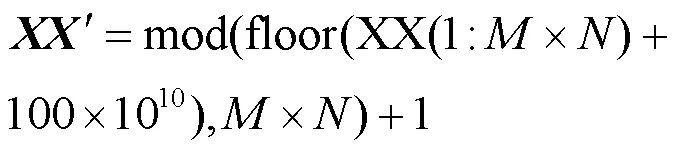
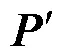
(6)语音解密。语音初次加密算法为对称加密算法,故解密为加密的逆过程。
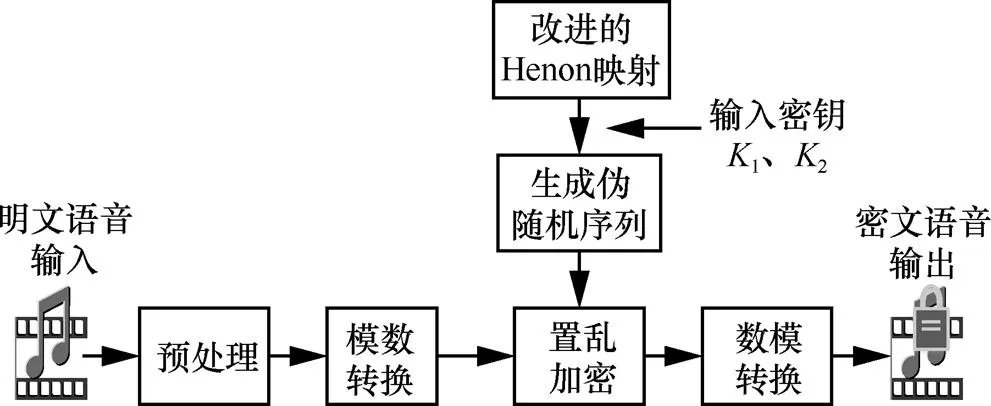
图4 语音初次加密算法处理流程
3.2 双重语音加密算法
本文提出的双重语音加密算法处理流程如图5所示,主要包括:密钥生成、改进的Henon置乱加密、Lorenz超混沌系统中Arnold置乱加密、异或扩散加密等步骤。
3.2.1 密钥生成
本文提出的加密系统属于对称加密系统,解密密钥和加密密钥必须完全相同才能正确解密。
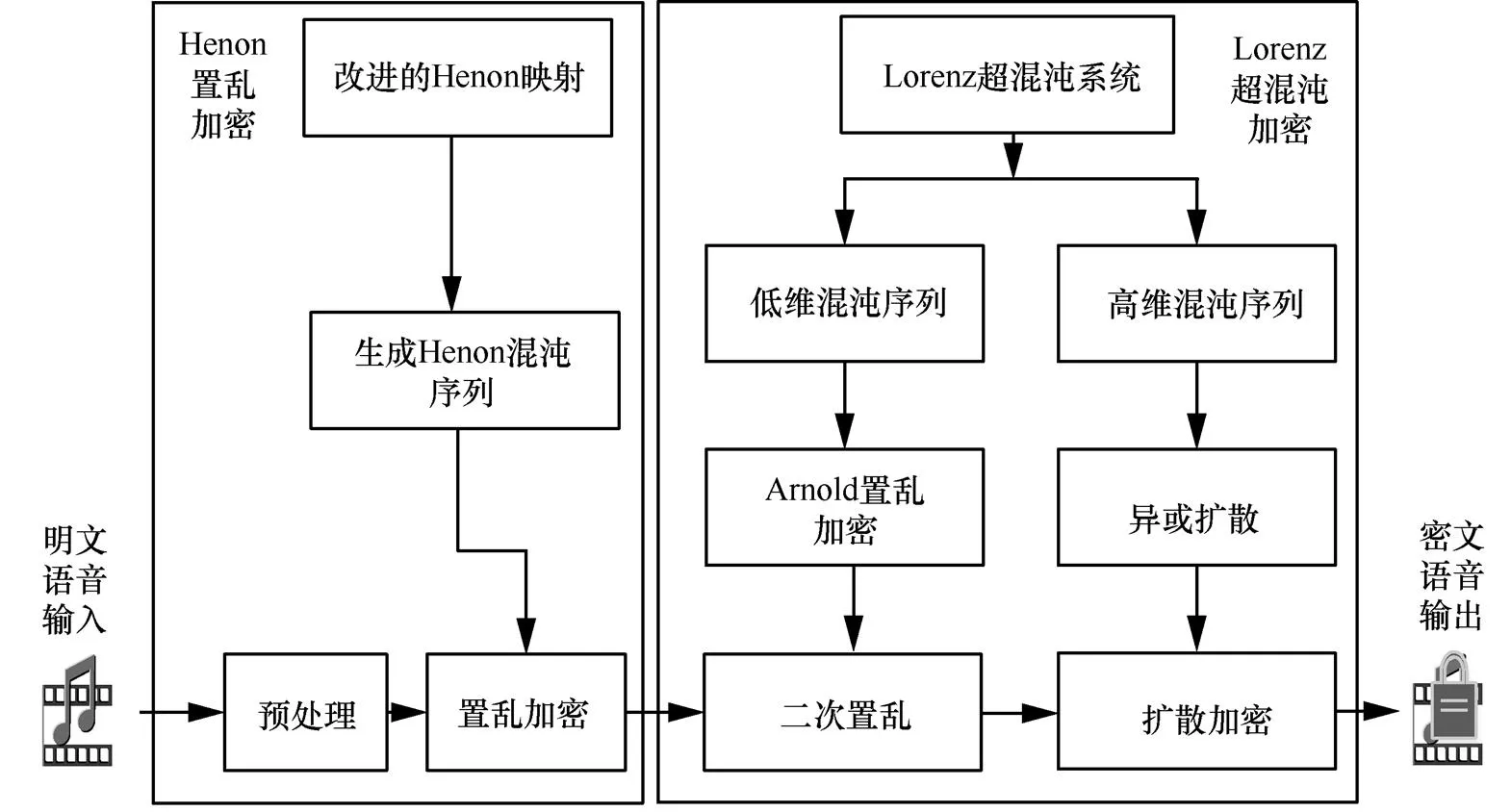
图5 双重语音加密算法处理流程
3.2.2 改进的Henon置乱加密
通常语音加密系统需要对语音数据先进行预处理操作。将模拟信号转换为数字信号,再利用混沌映射生成伪随机序列对语音数据加密。具体步骤包括以下几个。
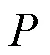
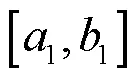
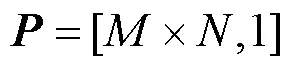
3.2.3 Lorenz超混沌语音加密
Lorenz超混沌语音加密系统主要包括多维混沌序列生成、Arnold置乱加密和按位异或扩散加密3部分组成。具体步骤如下。
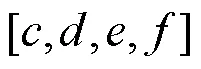
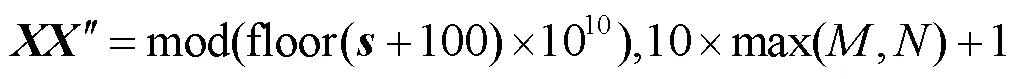
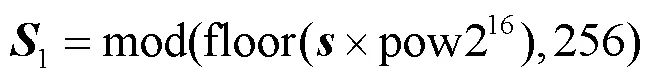
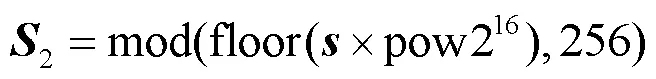
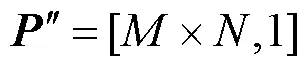
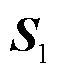
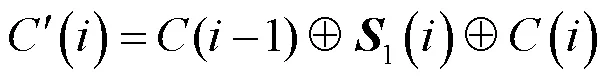
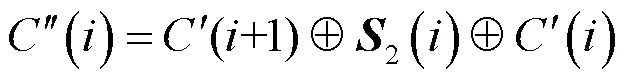
3.3 双重语音解密算法
本文提出的双重语音解密算法处理流程如图6所示。
双重语音解密处理具体步骤如下。
(2)混沌序列生成。使用与加密相同的密钥对Lorenz超混沌系统和改进的Henon混沌系统生成混沌序列。
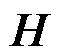
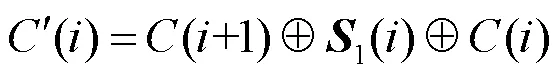
(14)
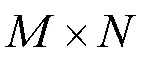
(6)解密语音重构。最后将解密后的语音数据重构恢复为时域语音信号,完成语音的解密过程。
3.4 对比论证分析
语音初次加密算法相较于双重语音加密算法在加密、解密性能和安全性等方面均有较大的差异,其具体区别如下。
(1)密钥空间。语音初次加密算法仅有两个密钥控制参数,相较于双重语音加密算法的6个密钥控制参数存在密钥空间小、安全性低等问题,不足以抵挡现有的密码学攻击等。
(2)加密时间分析。语音初次加密算法加密时间较快,主要原因是该加密算法结构简单、加密模块单一等。双重语音加密算法加密时间消耗略大,主要因素是该算法加密结构复杂、加密模块丰富,不仅进行了两次置乱加密且进行了正反向异或扩散加密。
(3)算法安全性分析。语音初次加密算法只针对语音帧的顺序进行了简单置乱操作,无法打乱语音帧相关联的统计特性,不能抵挡统计分析,存在安全性低、加密效果差、敏感信息易泄露等安全隐患。双重语音加密算法因其进行了两次置乱加密和正反向扩散加密,有效地打乱了语音数据相邻信号的统计特征,在保证语音加密数据安全性的同时也有较高的加密效率。
4 实验仿真和性能评估
为了评估本文语音加/解密系统的性能和效率,实验选用清华大学开放的汉语语音数据库THCHS-30[22]中的等长语音作为本次实验的测试语音进行加密、解密,其中,选取不同长度的语音类型各10条作为本次实验数据,见表1。实验硬件平台:Inter(R) Core(TM)i5-10200H CPU,3.17 GHz,内存16 GB。软件环境:Windows10、MATLAB R2017b软件实现编程和仿真。
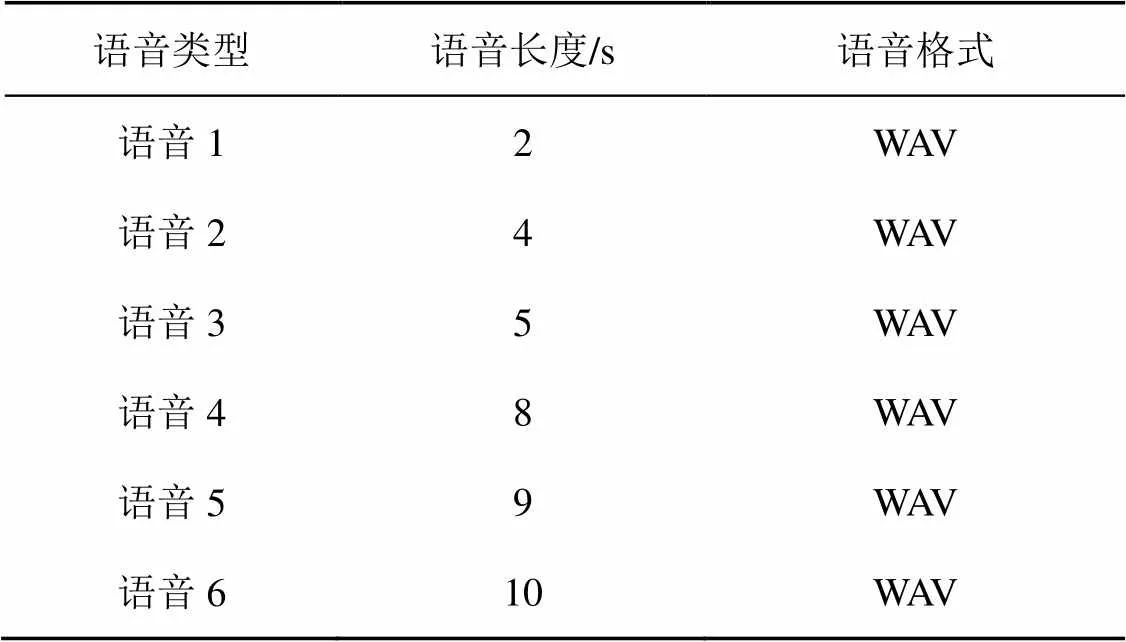
表1 测试语音类型
4.1 语音加密算法
4.1.1 密钥空间和密钥敏感度分析

以语音4为例生成的原始语音和两种加/解密语音波形图和频谱图如图7所示。混沌系统对密钥高度敏感,只有输入正确的密钥,才能完全解密出密文语音。即使密钥发生微小的变化时,无法正确地解密出原始语音。
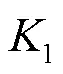
4.1.2 直方图分析
直方图[23]因其客观性和可视化被广泛应用于评估语音信号质量的方法之一。本次以语音3为例分析。本文两种加密算法的原始语音和加密语音的幅度直方图如图8所示。
图8(a)和图8(b)均有不规则的统计特征,图8(c)分布较为平稳,无较大的起伏和波动。说明语音初次加密算法无法打破语音数据的统计特征,相关性较高,不足以抵挡统计分析攻击;而双重语音加密算法对语音数据的统计特性具有较好的掩盖效果,相关性较差,统计信息少,足以抵挡统计攻击。
4.1.3 感知质量评估分析
感知语音质量评估(perceptual evaluation of speech quality,PESQ)是国际电信联盟电信标准化部P.862建议的客观平均意见得分(mean opinion score,MOS)[24]。通常取值从1.0(最差)~4.5(最好)的PESQ-MOS范围。
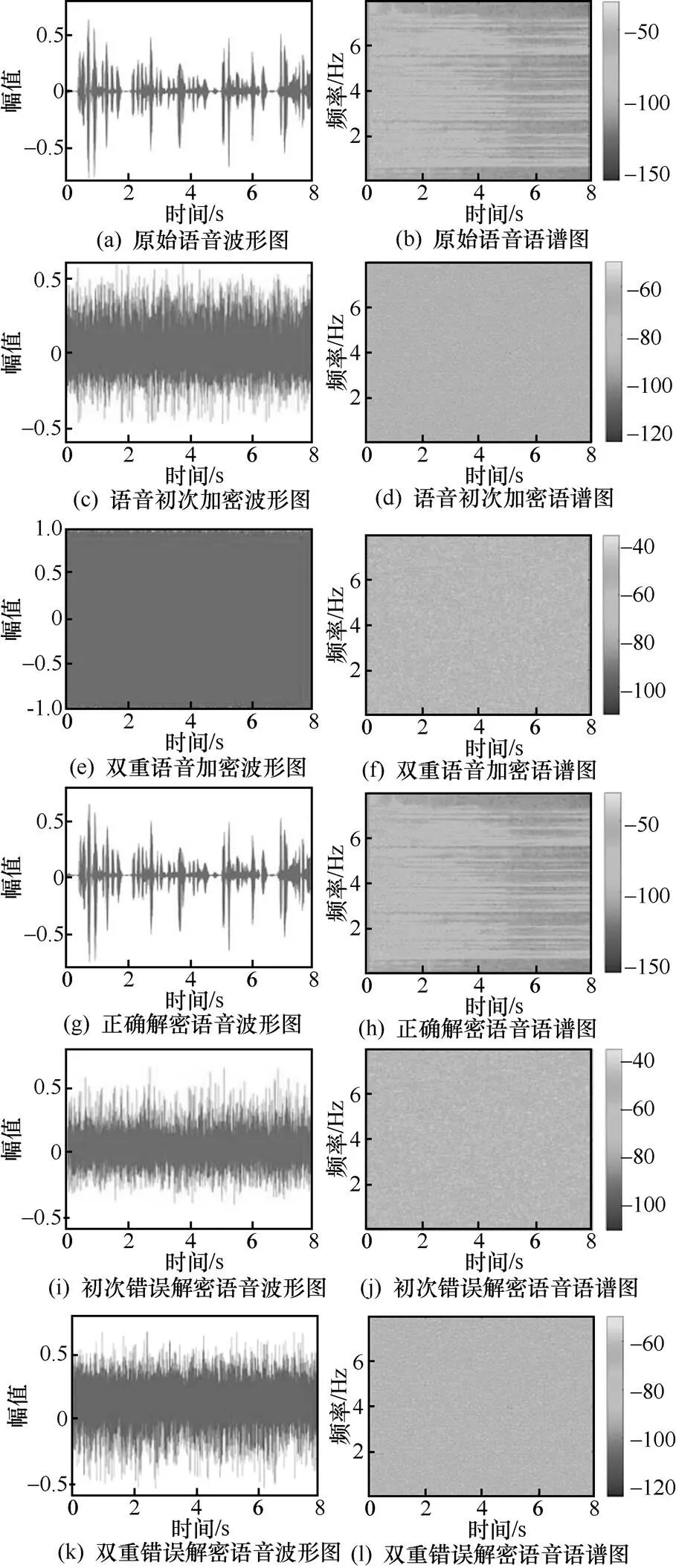
图7 原始语音和加/解密语音的波形图和语谱图
各项语音PESQ数值见表2。
由表2可知,两种加密算法所得到的加密语音PESQ值均在1以下,无法获得任何有效信息,而恢复的语音信号均为4.5,实现了无损恢复。因此,本文提出的两种加密算法均有较好的加密效果和无损解密性能。
4.1.4 信噪比和峰值信噪比分析
信噪比(signal noise ratio,SNR)[25]主要用于测量加密数据中信号的噪声含量和失真程度,被广泛应用于多媒体数据加密中。
信噪比的定义如式(15)所示。
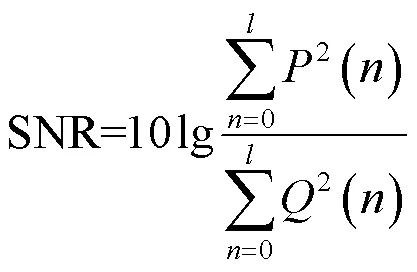
其中,为原始语音信号,为加密语音信号。
峰值信噪比(peak signal noise ratio,PSNR)[26]是原始语音信号最大功率与加密语音信号最大功率的比值。PSNR数值越低代表加密效果越好。峰值信噪比函数定义如式(16)所示。
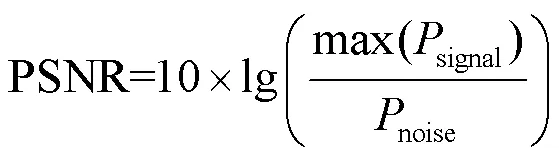
其中,signal表示原始语音信号功率,noise表示加密信号功率。
两种不同语音加密算法对语音信号的SNR和PSNR值见表3。
从表3可以看出,语音初次加密算法相较于双重加密算法的SNR数值和PSNR数值均较高,加密性能有待提高。双重语音加密算法的SNR和PSNR数值较低,满足语音加密指标要求,说明本文提出的双重语音加密算法具有很强的安全性。
4.1.5 相关分析
相关分析[27]作为一种数据统计方法,被广泛地应用于语音加密算法的性能评估。如果相关系数在+1或-1左右,则表明这两个语音信号相关性较强;如果两个语音信号相关系数在0左右,则代表这两个语音信号关联性极差。相关系数公式如式(17)~式(19)所示。
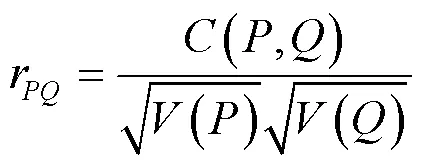
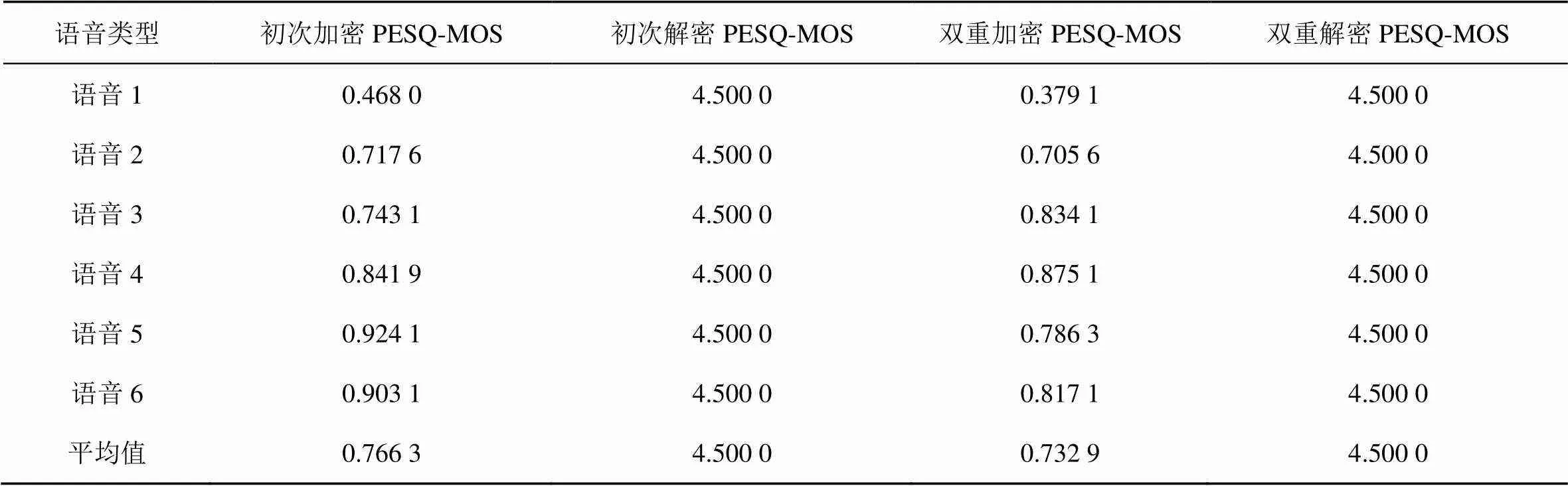
表2 加密与解密语音的PESQ-MOS数值数
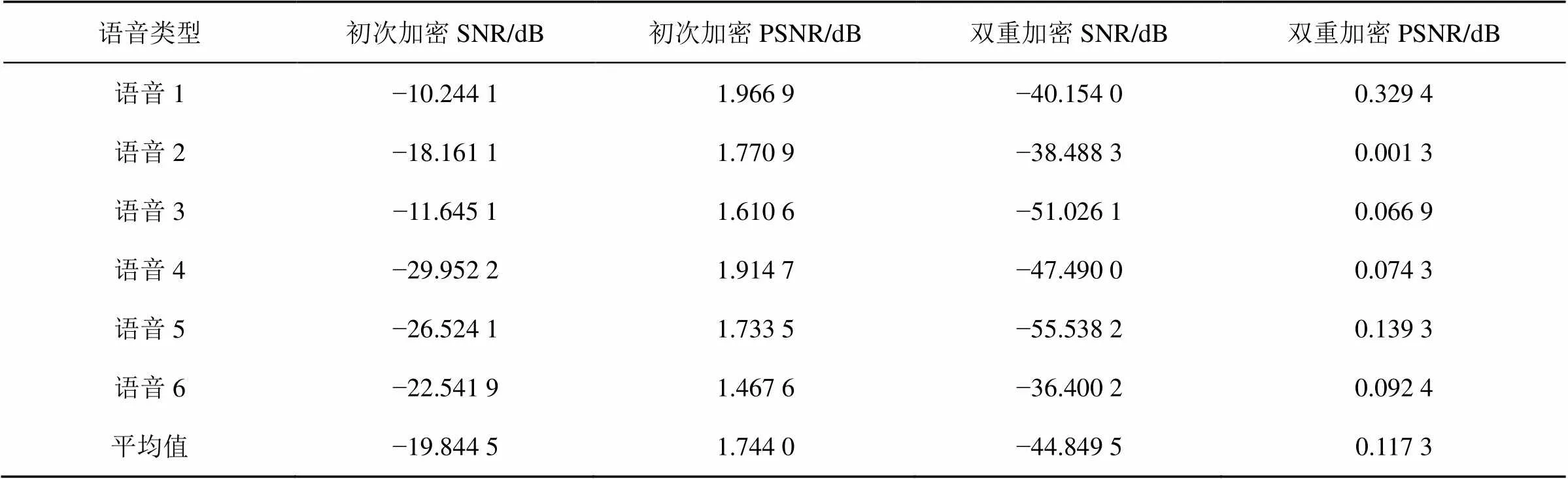
表3 加密语音的SNR和PSNR值
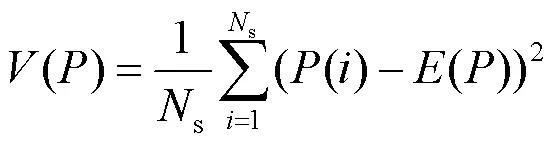
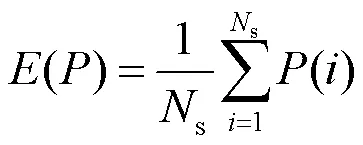
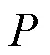
从表4可以看出,初次加密语音和双重加密语音的相关系数在0附近,表示原始语音和加密语音不相关,语音加密性能较好;初次解密语音和双重解密语音的相关系数在1附近,表明语音的恢复重构性能较强,可以实现无损恢复。但初次加密语音相较于双重加密语音的相关系数略高,加密性能有待提高。
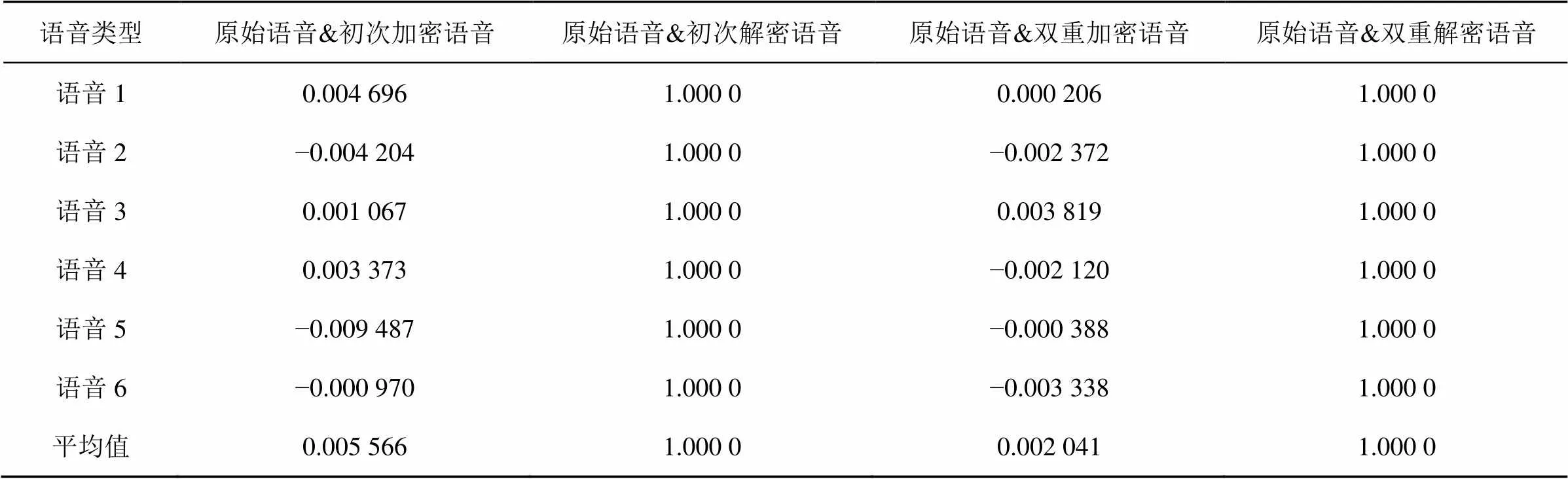
表4 语音的相关性分析
4.1.6 信息熵分析
信息熵分析主要用于语音加密数据中的错误率,通常信息熵的数值与语音的错误率成正比,加密语音数据的信息熵越高,代表语音加密效果越好,其定义如式(20)所示,如果加密的语音数据信息熵数值接近16,则表明该语音加密系统加密效率较好、安全性较高。
语音初次加密和双重语音加密的信息熵分析结果见表5。
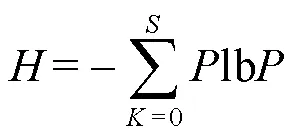
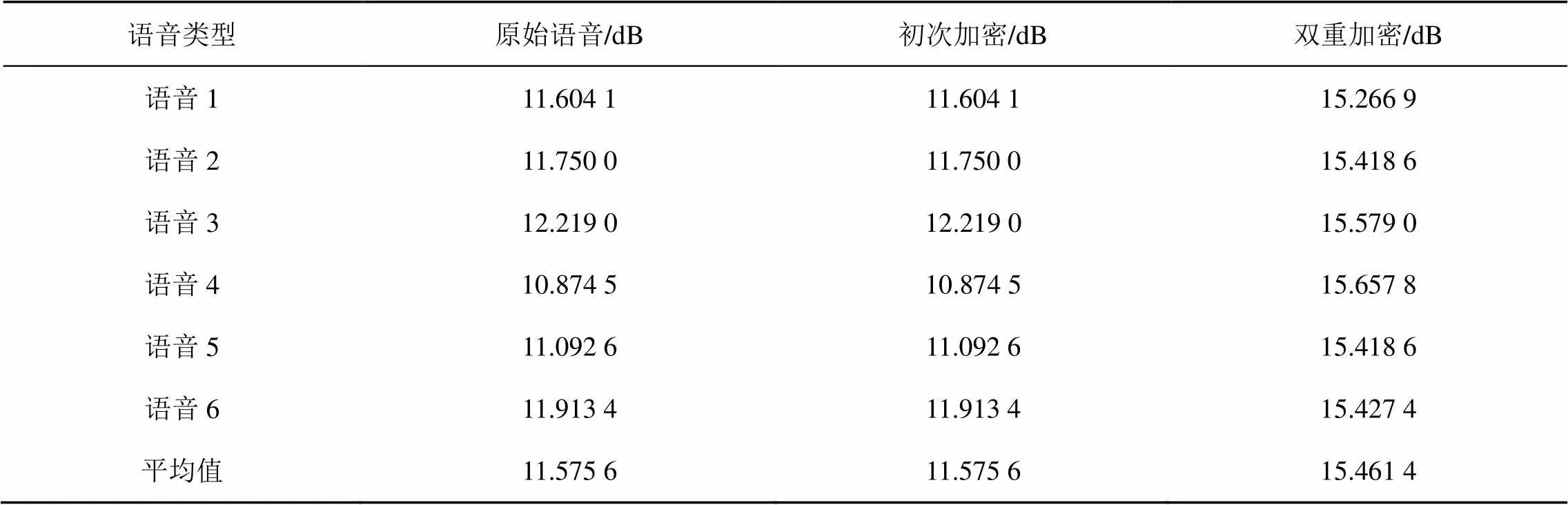
表5 语音的信息熵分析
从表5可以看出,语音初次加密的信息熵数值并没有改变,说明该加密方案无法抵御熵攻击,存在较高的安全性隐患;双重加密算法的加密语音数据信息熵均接近16,说明双重语音加密算法具有较高的安全性,足以抵抗熵攻击。
4.1.7 选择明文攻击分析
样本变化率(number of samples change rate,NSCR)[28]是一种选择明文攻击评价指标,它反映了两个语音数据相同位置不相等的数据点所占整个数据点的比例。如果NSCR近似等于100%,则认为加密算法性能较高,能够抵挡各种不同的明文攻击。
语音初次加密和双重语音加密的NSCR值见表6。
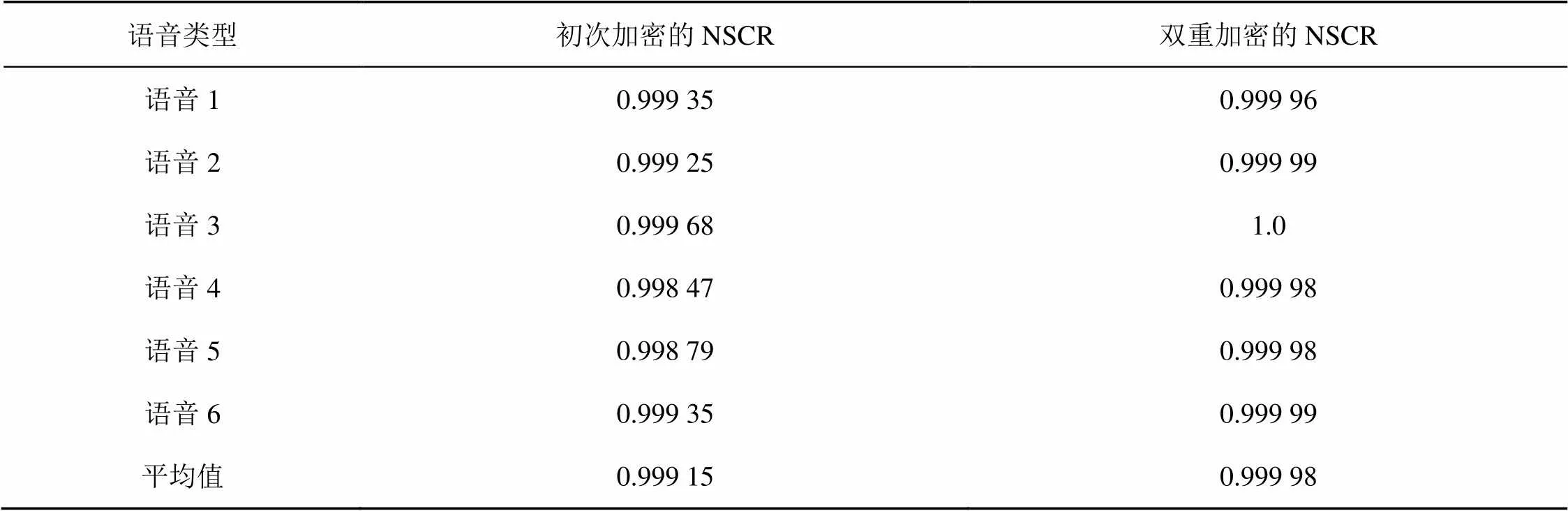
表6 选择明文攻击分析
从表6可知,本文提出的两种算法得到的NSCR数值均接近100%,表明加密后的语音数据样本点与原始语音截然相反,可以有效地抵挡差分攻击。语音初次加密算法相较于双重语音加密算法NSCR数值较低,说明双重语音加密更适用于语音数据的加密。
4.1.8 加/解密效率分析
语音加密系统的复杂度和语音的加密效率是相互制约的,现有的算法在确保密钥安全性时,往往忽略了语音的加/解密时间,并不能适用于海量的语音加密数据。语音初次加密和双重语音加密对不同语音长度的加/解密时间见表7。
由表7可知,本文对60条不同长度语音数据进行测试,实验结果表明语音初次加密算法加密每秒语音所用时间大约在0.07 s;双重语音加密加/解密每秒语音所需时长大约为0.11 s。根据语音时长,加密时间呈线性增长。语音初次加密算法相较于双重语音加密算法时间较少的主要原因是:初次加密算法结构单一、加密复杂度低、运算量小等因素,但两种加密算法结合密钥空间、加密安全性、加密效率、算法实时性等综合考虑,本文提出的双重语音加密算法具有较高的安全性和较好的加密效率,更适用于海量语音数据的安全加密。
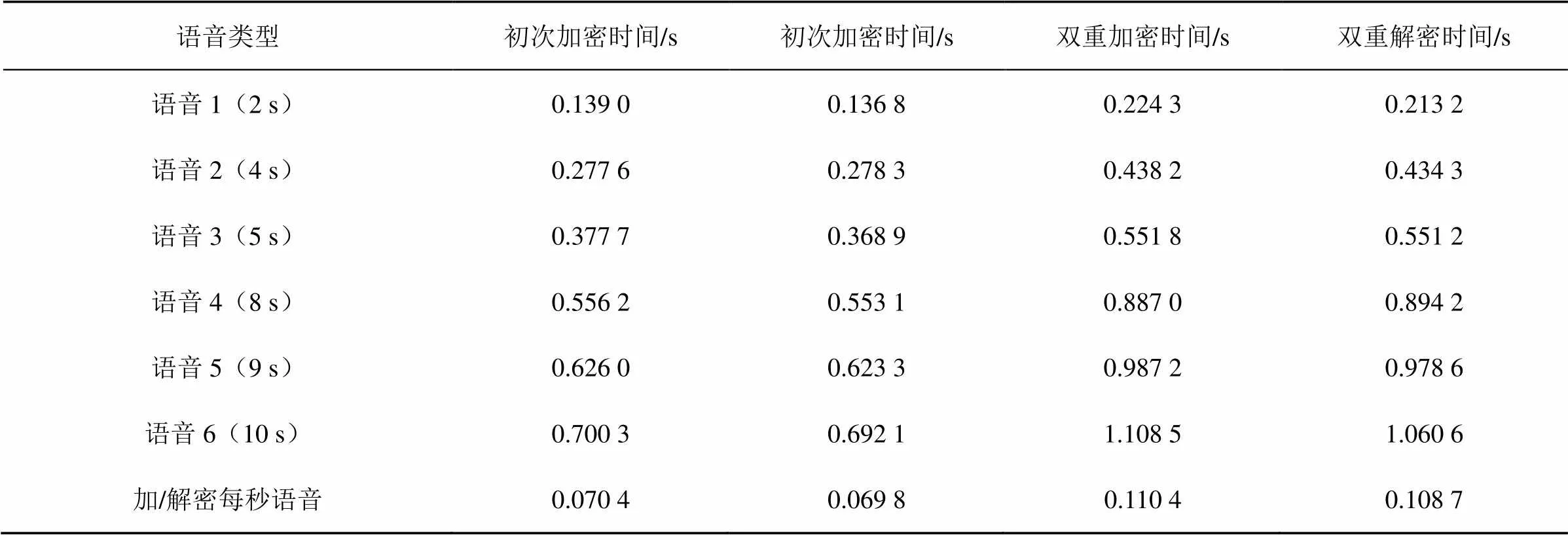
表7 加/解密效率分析
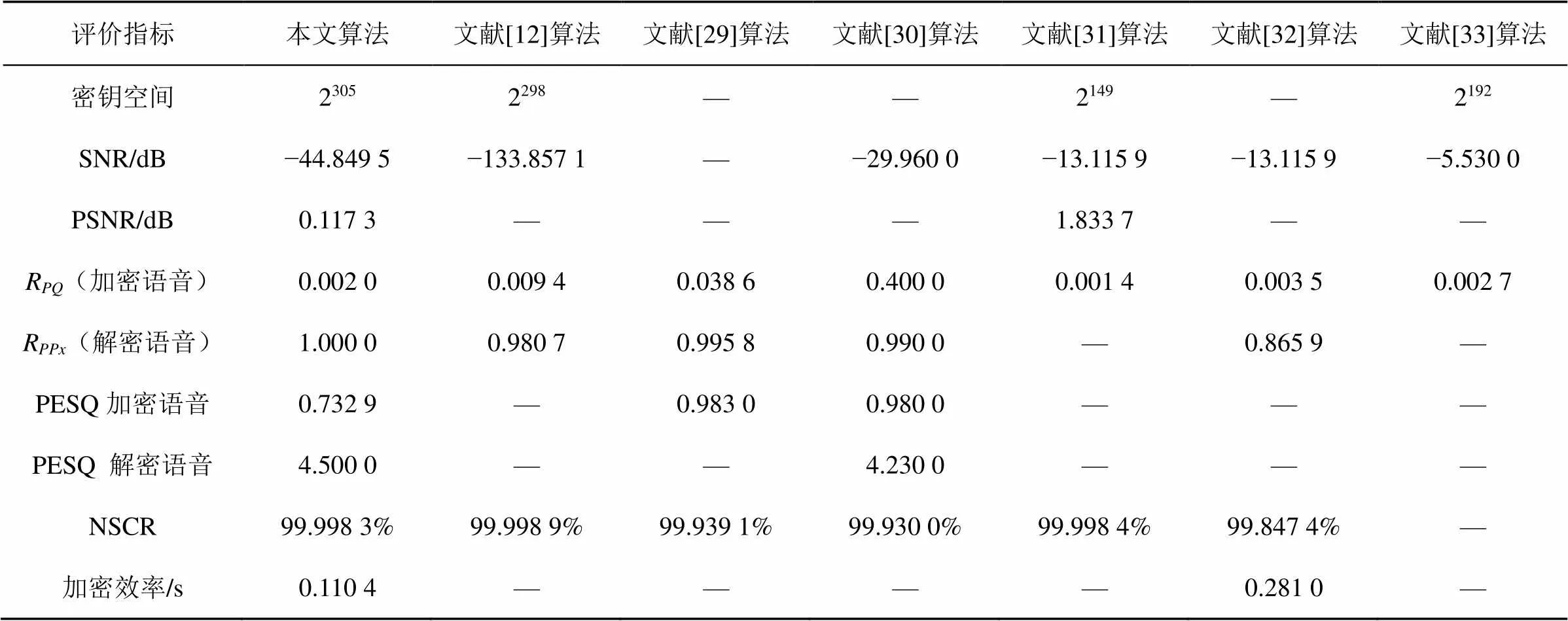
表8 与现有加密算法的性能对比结果
4.2 与现有加密算法性能对比
本文提出的双重语音加密算法与现有文献[12, 29-33]语音加密算法进行实验结果比较,对本文加密算法进行了客观准确的评价,对比数据均取自各项指标的平均值。本文算法与现有加密算法的性能对比结果见表8。
从表8可以看出,本文提出的双重语音加密算法从总体上优于文献[12, 29-33]的算法,主要原因是本文算法将语音数据先进行了一次二维的Henon置乱加密,又进行了超混沌加密,在保证良好加密安全性的同时又提高了加密效率。但文献[12]的SNR、文献[31]的NSCR、PQ性能优于本文。出现微小差值的原因是本文双重加密算法只进行了置乱和扩散加密,没有进行替换,除此之外不同的实验环境也会导致加密效率产生的微小差异等。
5 结束语
本文提出了一种基于改进Henon映射和超混沌的双重语音加密算法,并与语音初次加密算法进行性能比较分析,解决了现有语音混沌加密算法密钥空间小、加密效率低等问题。该方法在不改变系统控制参数的前提下,通过扩展控制参数范围,将经典的Henon映射控制变量修改为非线性三角函数变量,使得改进后的Henon映射具有更大的混沌空间和更高的混沌复杂度;将改进的Henon混沌系统与Lorenz超混沌系统相结合,并采用改进和优化的广义Arnold置乱算法,实现了语音数据的双重加密。实验结果表明,双重语音加密算法可以抵抗暴力攻击、差分攻击、统计攻击、熵攻击等,且具有较低的算法复杂性和较高的安全性,适用于海量语音数据的安全存储和隐私保护。未来的研究方向主要是将语音加密算法应用到数据流的实时传输中。
[1] SHAH D, SHAH T, JAMAL S S. Digital audio signals encryption by Mobius transformation and Hénon map[J]. Multimedia Systems, 2020, 26(2): 235-245.
[2] ZHENG J Y, LIU L F. Novel image encryption by combining dynamic DNA sequence encryption and the improved 2D logistic sine map[J]. IET Image Processing, 2020, 14(11): 2310-2320.
[3] SHI C, WANG H, HU Y, et al. A speech homomorphic encryption scheme with less data expansion in cloud computing[J]. KSII Transactions on Internet and Information Systems, 2019, 13(5): 2588-2609.
[4] ABRO F I, RAUF F, MOBEEN-UR-REHMAN, et al. Towards security of GSM voice communication[J]. Wireless Personal Communications, 2019, 108(3): 1933-1955.
[5] FUERTES W, MENESES F, HIDALGO L, et al. Rsa over-encryption implementation for networking: a proof of concept using mobile devices[J]. Investigacion Operacional, 2020, 41(4): 586-598.
[6] PATEL K. Performance analysis of AES, DES and Blowfish cryptographic algorithms on small and large data files[J]. International Journal of Information Technology, 2019, 11(4): 813-819.
[7] KAUR G, SINGH K, GILL H S. Chaos-based joint speech encryption scheme using SHA-1[J]. Multimedia Tools and Applications, 2021, 80(7): 10927-10947.
[8] SUHAIL K M A, SANKAR S. Image compression and encryption combining autoencoder and chaotic logistic map[J]. Iranian Journal of Science and Technology, Transactions A: Science, 2020, 44(4): 1091-1100.
[9] AL-HAZAIMEH O M. A new speech encryption algorithm based on dual shuffling Hénon chaotic map[J]. International Journal of Electrical and Computer Engineering (IJECE), 2021, 11(3): 2203.
[10] AL-HAZAIMEH O M. A new dynamic speech encryption algorithm based on Lorenz chaotic map over Internet protocol[J]. International Journal of Electrical and Computer Engineering (IJECE), 2020, 10(5): 4824.
[11] SAYED W S, TOLBA M F, RADWAN A G, et al. FPGA realization of a speech encryption system based on a generalized modified chaotic transition map and bit permutation[J]. Multimedia Tools and Applications, 2019, 78(12): 16097-16127.
[12] FARSANA F J, DEVI V R, GOPAKUMAR K. An audio encryption scheme based on Fast Walsh Hadamard Transform and mixed chaotic keystreams[J]. Applied Computing and Informatics, 2020.
[13] HAMDI M, RHOUMA R, BELGHITH S. An appropriate system for securing real-time voice communication based on ADPCM coding and chaotic maps[J]. Multimedia Tools and Applications, 2017, 76(5): 7105-7128.
[14] ZGHAIR H K, MEHDI S A, SADKHAN S B. Speech scrambler based on discrete cosine transform and novel seven-dimension hyper chaotic system[J]. Journal of Physics: Conference Series, 2021, 1804(1): 012048.
[15] SHAH D, SHAH T, AHAMAD I, et al. A three-dimensional chaotic map and their applications to digital audio security[J]. Multimedia Tools and Applications, 2021, 80(14): 22251-22273.
[16] IMRAN O A, YOUSIF S F, HAMEED I S, et al. Implementation of El-Gamal algorithm for speech signals encryption and decryption[J]. Procedia Computer Science, 2020, 167: 1028-1037.
[17] ELSAFTY A H, TOLBA M F, SAID L A, et al. Hardware realization of a secure and enhanced s-box based speech encryption engine[J]. Analog Integrated Circuits and Signal Processing, 2021, 106(2): 385-397.
[18] HÉNON M. A two-dimensional mapping with a strange attractor[J]. Communications in Mathematical Physics, 1976, 50(1): 69-77.
[19] STEWART I. The Lorenz attractor exists[J]. Nature, 2000, 406(6799): 948-949.
[20] 薛伟, 王磊. 一种基于新型混沌的彩色图像加密算法[J]. 光学技术, 2018, 44(3): 263-268.
XUE W, WANG L. A color image encryption algorithm based on novel chaos[J]. Optical Technique, 2018, 44(3): 263-268.
[21] PAN T G, LI D Y. A novel image encryption using Arnold cat[J]. International Journal of Security and Its Applications, 2013, 7(5): 377-386.
[22] WANG D, ZHANG X W. THCHS-30: a free Chinese speech corpus[J]. CoRR, 2015.
[23] NASKAR P K, PAUL S, NANDY D, et al. DNA encoding and channel shuffling for secured encryption of audio data[J]. Multimedia Tools and Applications, 2019, 78(17): 25019-25042.
[24] Perceptual evaluation of speech quality (PESQ): an objective method for end-to-end speech quality assessment of narrow-band telephone networks and speech codecs[EB]. 2001.
[25] BABU N R, KALPANA M, BALASUBRAMANIAM P. A novel audio encryption approach via finite-time synchronization of fractional order hyperchaotic system[J]. Multimedia Tools and Applications, 2021, 80(12): 18043-18067.
[26] SHEELA S J, SURESH K V, TANDUR D. Image encryption based on modified Henon map using hybrid chaotic shift transform[J]. Multimedia Tools and Applications, 2018, 77(19): 25223-25251.
[27] AUGUSTINE N, GEORGE S N, PATTATHIL D P. An audio encryption technique through compressive sensing and Arnold transform[J]. International Journal of Trust Management in Computing and Communications, 2015, 3(1): 74.
[28] BELAZI A, ABD EL-LATIF A A, BELGHITH S. A novel image encryption scheme based on substitution-permutation network and chaos[J]. Signal Processing, 2016, 128: 155-170.
[29] SATHIYAMURTHI P, RAMAKRISHNAN S. Speech encryption algorithm using FFT and 3D-Lorenz–logistic chaotic map[J]. Multimedia Tools and Applications, 2020, 79(25): 17817-17835.
[30] SOLIMAN N F, KHALIL M I, ALGARNI A D, et al. Efficient HEVC steganography approach based on audio compression and encryption in QFFT domain for secure multimedia communication[J]. Multimedia Tools and Applications, 2021, 80(3): 4789-4823.
[31] KORDOV K. A novel audio encryption algorithm with permutation-substitution architecture[J]. Electronics, 2019, 8(5): 530.
[32] KHOIROM M S, LAIPHRAKPAM D S, TUITHUNG T. Audio encryption using ameliorated ElGamal public key encryption over finite field[J]. Wireless Personal Communications, 2021, 117(2): 809-823.
[33] FARSANA F J, GOPAKUMAR K. Private key encryption of speech signal based on three dimensional chaotic map[C]//Proceedings of 2017 International Conference on Communication and Signal Processing (ICCSP). Piscataway: IEEE Press, 2017: 2197-2201.
A dual speech encryption algorithm based on improved Henon mapping and hyperchaotic
ZHANG Qiuyu, SONG Yujie
School of Computer and Communication, Lanzhou University of Technology, Lanzhou 730050, China
Aiming at the problems of small key space, poor security, low encryption efficiency, and the inability to realize the trade-off between key complexity and encryption efficiency of existing speech chaotic encryption algorithms, a dual speech encryption algorithm based on improved Henon mapping and hyperchaotic was proposed. Firstly, the traditional Henon mapping was improved by extending the control parameter range and taking the nonlinear trigonometric function as the input parameter variable, which made the Henon mapping have larger chaotic space and higher chaotic complexity. Secondly, the improved Henon mapping was used to generate pseudorandom sequence, and the speech data was encrypted single time without repeated scrambling to obtain the first time encryption results of the speech data. Finally, Lorenz hyperchaotic system was adopted to encrypt the speech data after the first time encryption by Arnold secondary scrambling encryption and XOR diffusion encryption to obtaining the final ciphertext speech data. The experimental results show that, compared with the existing methods, the proposed algorithm have larger key space, higher encryption efficiency, and stronger robustness against various cryptographic attacks.
speech encryption, improved Henon mapping, Lorenz hyperchaotic system, Arnold transform, robustness
TP309
A
10.11959/j.issn.1000−0801.2021271
2021−09−09;
2021−12−10
国家自然科学基金资助项目(No.61862041)
The National Natural Science Foundation of China (No.61862041)

张秋余(1966− ),男,兰州理工大学博士生导师,主要研究方向为网络信息安全、智能信息处理与模式识别等。
宋宇杰(1994− ),男,兰州理工大学硕士生,主要研究方向为网络信息安全、密文语音检索等。

