平方耦合光力系统中光传输研究

于 凯 贾 晓

（南阳理工学院信息工程学院，河南 南阳 473004）

0 引言

近年来，通过调整光与1个或多个机械振子的相互作用来控制光的传播的研究取得了许多成果。一种类似于原子物理学中电磁感应透明现象[1]，即光力诱导透明[2]，这一现象在最近的理论和试验上都得到了证实。在最近几十年的研究中，有关于光和机械振子耦合的研究大多数都是线性耦合的[3]。除了经典线性耦合的光力系统外，还存在一个平方耦合的光力系统[4]，即光腔场与机械振子位移的平方相互耦合。与线性耦合不同，平方耦合是双声子过程，而线性耦合只涉及单声子过程，这使平方耦合能提供更多复杂的非线性效应。Huang和Agarwal分析了在平方耦合膜系统中也会出现的光力诱导透明效应，并解释了环境温度及其他系统参数影响平方耦合光力系统中出现透明窗口[5]的原因。平方耦合腔光力系统表现出复杂的干涉效应，导致信号场从不透明传输到透明再到被显著放大[6]。这些现象取决于光力耦合的强度、弱相干驱动场的振幅和外加场的相位。因此，平方耦合的光机械系统可以用作光学晶体管，其中信号场可以被视为由控制场和探测场控制。首次观察到电磁诱导透明现象是在原子蒸气中，最近在量子阱、超材料等各种固体系统中也观察到了电磁诱导透明现象。对腔光力学系统来说，在光学领域和微波领域都已经观察到基于光力诱导透明的慢光与快光现象。

1 系统结构模型与动力学方程

1.1 物理结构

平方耦合光力系统原理图如图1所示。由1个振幅为εS、频率为ωS的强探测场和1个振幅为εc、频率为ωc的弱探测场共同驱动。机械谐振器的位置用x表示，l是法布里-珀罗腔的长度，kL=ηLk（kR=ηRK）表示左（右）镜的空腔衰减率（K为总衰减率）。其中，总损耗率k=kL+kR+k0，k0表示系统固有损耗率，kL和kR分别表示左边和右边镜子的耗散率，耦合参数ηL（ηR）可连续调节，选择ηL=ηR=0.499。强控制场振幅为εS、频率为ωS，弱探测场振幅为εc、频率为ωc，力学驱动振幅为εd、频率为ωd，εt-out表示输出场振幅。

图1 平方耦合光力系统原理图

1.2 动力学方程

该平方耦合光力系统的哈总密顿量如公式（1）所示。

式中：δa为湮灭算符的波动值；δp为系统动量的波动值；δP为动量平方的波动值；A1+为湮灭算符一阶上边带系数；A1-为湮灭算符一阶下边带系数；A2+为湮灭算符二阶上边带系数；A2-为湮灭算符二阶下边带系数；x1为位移一阶上边带系数；x1*为位移一阶下边带系数；x2为位移二阶上边带系数；x2*位移二阶下边带系数；p1为动量一阶上边带系数；p1*动量一阶下边带系数；p2为动量二阶上边带系数；p2*为动量二阶下边带系数；X1为位移平方的一阶上边带系数；X1*为位移平方的一阶下边带系数；X2为位移平方的二阶上边带系数；X2*为位移平方的二阶下边带系数；P1为动量平方的一阶上边带系数；P1*为动量平方的一阶下边带系数；P2为动量平方的二阶上边带系数；P2*为动量平方的二阶下边带系数；Q1为动量平方的一阶上边带系数；Q1*为动量平方的一阶下边带系数；Q2为动量与位移乘积的二阶上边带系数；Q2*为动量与位移乘积的二阶下边带系数。

基于系统的光力非线性，输出场有一系列的频率分量（ωc±nω）产生，整数n是边带的阶数。A1±表示一阶边带的系数，频率为ωc±Ω。其中，一阶上边带ωc+Ω被称为反斯托克斯场，一阶下边带ωc-Ω被称为斯托克斯场。该文只关注一阶边带和二阶边带的过程，忽略其他频率分量。

该文重点讨论输出场的分量，它通过法布里-珀罗腔的右镜传输，并在信号场的频率上振荡。利用输入和输出理论，可以得到法布里-珀罗腔传输的输出场如公式（9）所示。

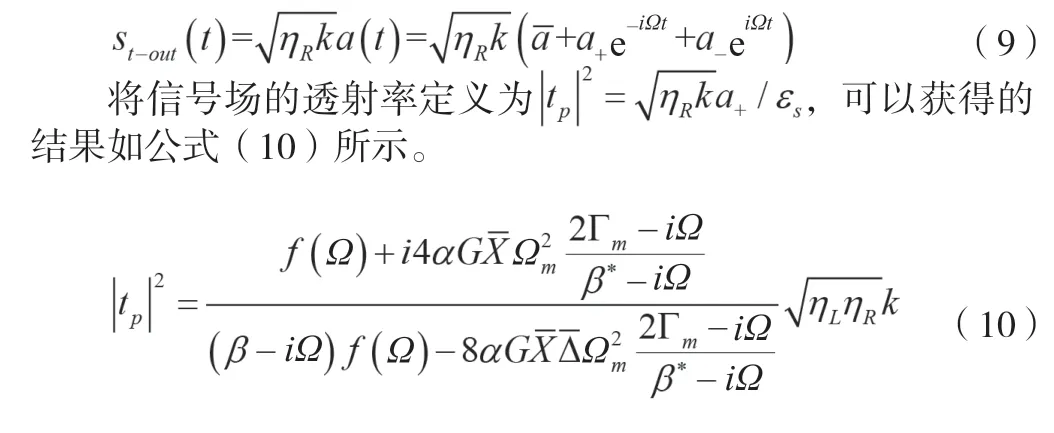
公式（10）表示信号和耦合场的贡献，它在平方耦合光力系统中引起光机械诱导的不透明度。结果表明，信号场探测法布里-珀罗腔有3条途径：通过右镜直接透过光耦；通过2个声子过程干扰磁共振散射的耦合场；通过2个声子过程干扰磁共振直接机械驱动散射的声子散射的耦合场。因此，信号场的透射谱是由这3条路径的干涉决定的。其中，耦合功率Pc、相位差φ和机械驱动场的振幅εd发挥了重要的作用。

2 系统参数对系统透射谱线的影响

2.1 不同功率激光场的驱动对探测场透射率的影响

该文选择的所有参数都来自于最近的试验。可以清楚地看到，在平方耦合机制下，探测场的透射率随着失谐量的变化的谱线图如图2所示。探测场透射率是指将一束探测光入射到平方耦合腔光力系统后，透过该系统的探测光的光通量与入射探测光的光通量的比值。失谐量为控制场与探测场之间频率的差值。

图2中|tp|2表示探测光的透射率，Ω=ωs-ωc是信号和耦合场之间的失谐量，Ωm=2 π×0.1 MHz为振子频率，驱动功率为50 μW。

图2 平方耦合机制下，探测场的透射率随着失谐量的变化图

图2（a）在平方耦合机制下，受驱动场影响的探测场透射率随着失谐量的增加不断变化，在失谐量Δ=2 Ω时，控制场产生的反斯托克斯光与探测光发生干涉形成共振。图2（b）增大驱动场的幅值，在该驱动场的影响下，在失谐量Δ=2 Ω时，探测场透射率发生变化，出现了1个很小的透明窗口。出现透明窗口的原因为探测场与驱动场2个频率不同的激光形成1个拍频，拍频驱动振子，在该过程中出现非线性的上下转换，产生反斯托克斯光，一阶边带需要转换1次，二阶边带需要转换2次，控制场失去2个振子，吸收或增加1个振子为反斯托克斯光。反斯托克斯场与探测场之间是共振的，反斯托克斯场与探测场的频率相同，在腔场内方向一致，相位差恒定。即反斯托克斯场与探测场会发生相消干涉，从而使探测场的透射谱线在控制场与探测场失谐量和机械振子频率匹配处出现1个透明窗口。图2（c）继续增大驱动场的幅值，在该驱动场的影响下，当失谐量为1.5 Ω～2.0 Ω时，探测场透射率逐渐减少，而当失谐量为2.0 Ω～2.5 Ω时，探测场透视率逐渐增大。当失谐量为Δ=2 Ω时，探测场透射率发生突变，此时，探测场透射率等于0.6，出现很明显的透明窗口。图2（d）继续增大驱动场的幅值，在该驱动场的影响下，在失谐量为1.5 Ω～2.0 Ω时，探测场透射率逐渐减少，在失谐量2.0 Ω～2.5 Ω时，探测场透视率逐渐增大。在失谐量Δ=2Ω时，探测场透射率发生突变，此时探测场透射率趋近于1，即探测光被完全吸收。由于图2中驱动场幅值的不同，因此会导致透射率谱线出现很大差异。其中，透明窗口出现的物理过程为控制场产生的反斯托克斯光与探测光发生相消干涉，使探测场的透射谱线在控制场与探测场失谐量和机械振子频率匹配处出现1个透明窗口。而驱动场的功率大小会影响反斯托克斯场的出现，不能使所有的探测光都与反斯托克斯场发生相消干涉，影响透明窗口的出现。

2.2 温度对透明窗口的影响

透明窗口（光力诱导透明现象）可以由泵浦光与探测光之间的拍频Ω=ωp-ωl振荡的辐射压力来解释，透明窗口出现的原因为如果驱动力接近于机械共振频率Ωm，则振动模相干激发，导致强控制场光产生斯托克斯散射和反斯托克斯散射。如果在腔的红边带驱动光学腔，腔场内的斯托克斯的散射过程将被抑制，只剩下反斯托克斯散射。当探测光与腔发生谐振时，控制场产生的反斯托克斯场与探测场之间是共振的，它们之间满足干涉的条件，反斯托克斯场与探测场的频率相同，在腔场内方向一致，相位差恒定。即反斯托克斯场与探测场会在法布里-珀罗腔内发生干涉，并导致出现透明窗口。

改变环境的温度，选取T=50 K。将图3的透射率谱线图与图2进行对比，升高温度，透明窗口会变宽，出现了本征模式劈裂，透射率谱线从尖锐变得圆滑。如果继续升高温度，那么谱线会出现2次吸收凹陷，此时透明窗口消失。通过分析透射率谱线图可以得出，温度的变化很大程度地影响了透明窗口的大小，当温度过大时会导致透明窗口消失。

图3 T=50 K时，失谐量对透射率的影响

3 结论

综上所述，该文介绍了腔力光学的研究历史、当前研究现状以及非线性的平方耦合光力系统的模型，通过分析该模型，在双色激光场包括控制场和探测场驱动在内的情况下，根据量子光学的基本知识写出系统的哈密顿量以及其相应的海森堡-朗之万运动方程。当控制场的强度远远大于探测场的强度时，即在微扰机制的条件下时，可以将系统运动方程中的光力非线性项线性化。在半经典近似的条件下，将运动方程中的算符写为平均值和小量涨落的和，并忽略其高阶小量，只保留到一阶小量，从而得到线性化的运动方程。根据该线性化的运动方程可以求解一阶边带即探测场振幅的解析表达式。最后通过MATLAB对理论计算的结果进行数值模拟并画图，进一步探究系统参数对探测场透射率的影响。该文主要探究了不同功率激光场的驱动对探测场透射率的影响以及温度对透明窗口的影响。

驱动场功率的大小会影响斯托克斯散射，从而使腔场内反斯托克斯场与探测场发生不完全的相消干涉，影响透明窗口的出现。温度也会影响透明窗口的大小，当温度过大时，会出现本征模式劈裂，从而导致透明窗口消失。