基于遗传算法的一种串联机构性能指标分析

王学雷，张 宾，冯志新，吕世霞

（1.北京电子科技职业学院，北京 100176；2.中国农业大学工学院，北京 100083）

1 引言

串联机器人是一个开式运动链，这种结构决定了串联机器人在工作空间和姿态调整上具有较高的灵活性和柔性，因此串联机器人在工业自动化中有着广泛应用[1-6]。

机器人运动学性能好坏直接影响其运动效果，为此，研究者提出多种性能指标来评价机器人的运动学性能，为机器人优化设计提供了依据[7-12]。

1991年，文献[7]基于雅可比矩阵首次定义了机器人全域性能指标。2012年，文献[8]应用动力学性能指标对4 自由度SCARA并联机构进行了优化设计。2015年，文献[9]对Tricept 并联机构的笛卡尔工作空间进行了优化。2019年，文献[10]选取了兼顾全域性能指标和全域条件波动指标的优化函数对机器人进行了优化设计。文献[11]提出了机构运动性能的全局尺度分析方法，为仿生机械腿的设计和全局尺度分析提供了一般的理论和方法。这些研究均针对一种具体的机器人机构进行研究，仍存在评价不全面、不系统等问题，计算过程复杂，工作量大，没有形成一个确切的全局综合性能评价指标，因此建立一种能全面反映机器人运动学性能的通用性强的性能评价指标对机器人进行优化设计有着重要意义，针对6R串联机构的优化设计还亟待研究与改进。

针对机器人速度同性指标、灵巧度指标和全域性能波动指标的不足，根据加权法，提出一种改进的全域综合性能评价指标对6R 串联机构进行性能指标分析，该分析方法可用于对其它机器人的性能分析，可更全面的分析机器人运动学性能，具有通用。基于改进后的全域综合性能评价指标，利用遗传算法求得了6R串联机构性能较好的尺寸，为机器人关键部件的尺寸选取提供了理论依据。

2 6R串联机构介绍

一种六自由度混联机器人可简化为2SPU+U+RRRR，如图1（a）所示。其两自由度并联部分由两个驱动分支2SPU和一个约束分支U构成，将两驱动分支2SPU对约束分支U的驱动作用等效为由组成U副的两个转动副RR提供，这样2SPU+U并联机构可简化为两自由度串联机构RR，即2SPU+U+RRRR六自由度混联机器人可简化为一个两自由度串联机构RR 末端串联四自由度串联机构RRRR，等效为六自由度6R 串联机构，如图1（b）所示。其结构简图，如图1（c）所示。

图1 6R串联机构Fig.1 6R Serial Mechanism

3 6R串联机构全域综合性能评价指标分析

设串联机构输出速度和输入速度之间的映射关系，如下式所示：

式中：Vc—串联机构末端执行器输出速度；v—串联机构末端执行器输出线速度；ω—串联机构末端执行器输出角速度；θ˙∈n—串联机构各关节输入速度；J∈n—串联机构速度雅可比矩阵。

定义串联机构速度雅可比矩阵J=[Jv Jω]T，式中：Jv∈R3×n—线速度雅可比矩阵；Jω∈R3×n—角速度雅可比矩阵，则式（1）可写为如下表达式：

式中：ηcv—线速度灵巧度评价指标；

ηcω—角速度灵巧度评价指标；

Kcv—线速度条件数；

Kcω—角速度条件数，且0＜ηcv≤1，0＜ηcω≤1，ηcv和ηcω的值越大，机构灵巧度越高。

基于统计学中变异系数概念得6R串联机构线速度和角速度全域性能波动指标如下：

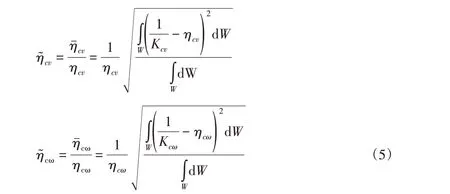
采用加权求和原理，采用一种基于速度同性指标、灵巧度指标和全域性能波动指标的全域综合性能评价指标ηcξξ来综合评价机器人的运动性能，如式（6）所示：

采用单变量分析法分别绘制6R 串联机器人重要结构参数a1和d1对全域综合性能指标ηcξξ的影响规律，借助Matlab 软件分别绘制a1和d1对全域综合性能指标ηcξξ的影响曲线，得到关系曲线，如图2所示。

仅考虑a1变化时对ηcξξ的影响规律，如图2（a）所示；仅考虑d1变化时对ηcξξ的影响规律，如图2（b）所示，其余参数均按照初始设定参数进行赋值。

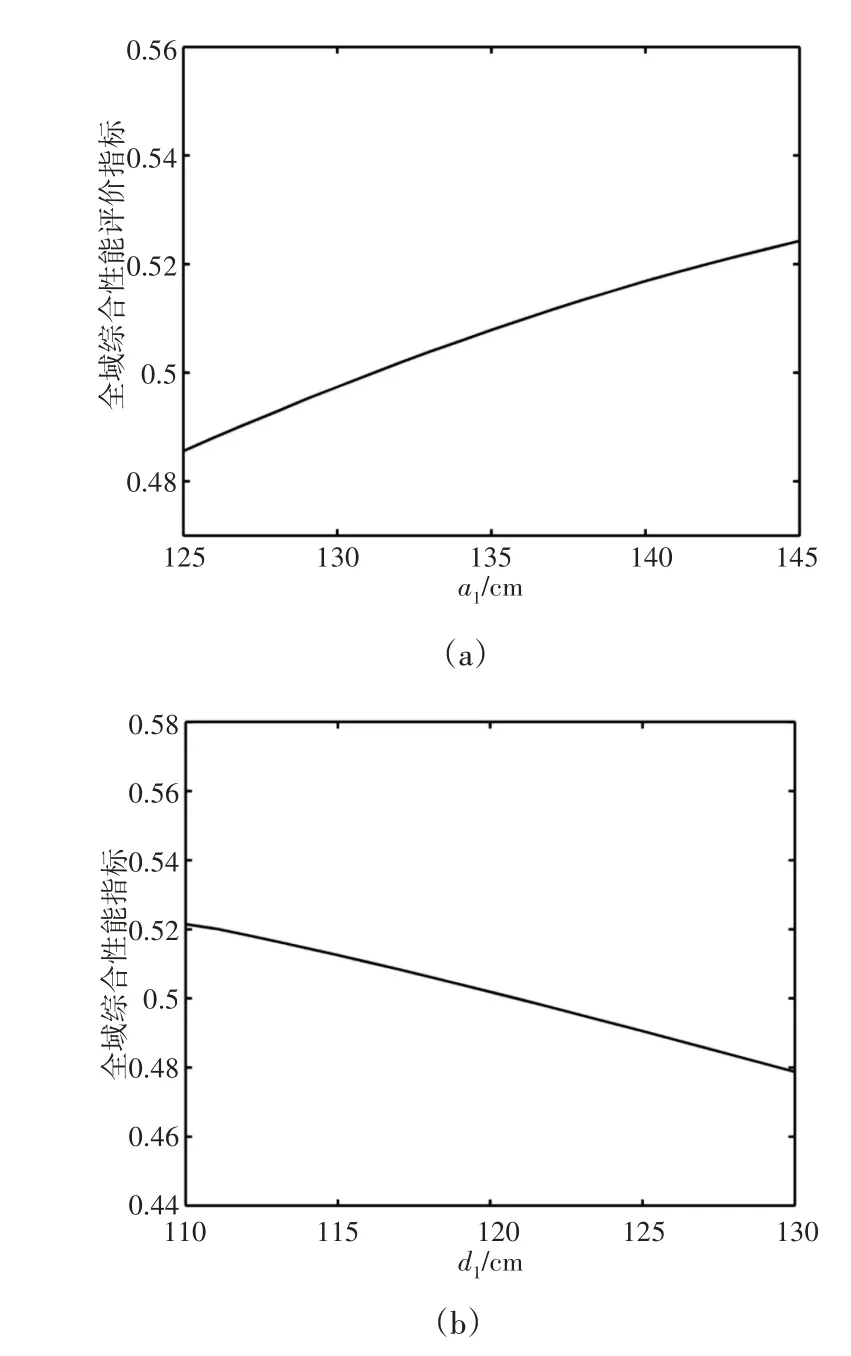
图2 结构参数与ηcξξ的关系Fig.2 Relationship Between Structural Parameters and ηcξξ

从图2可以看出，随着a1值的增大，ηcξξ随之增大，且类似线性规律变化，说明a1值的增大会使机构全域综合性能指标增大，有利于机构的运动控制。随着d1值的增大，ηcξξ随之减小，也类似线性规律变化，说明d1值的增大会使整个机构全域综合性能指标减小，不利于机构的平稳运行。

4 基于遗传算法的全域综合性能指标优化研究

如何确定机器人各构件尺寸是其优化设计的难题之一，机器人优化设计前，常根据其功能及实际应用，给出各构件尺寸的变化范围。

4.1 目标优化函数

对上述性能指标优化的原理是通过加权求和法将多目标优化问题转化为单目标优化问题，可看作为满足不同约束条件下的非线性规划问题，优化目标函数为：

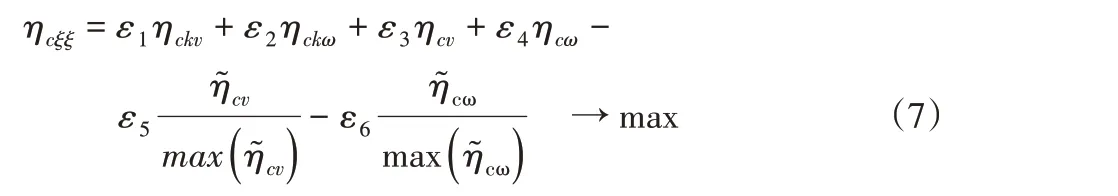
4.2 设计变量

对于本文的6R串联机构，对目标函数影响较大的参数有a1和d1，因此，该目标函数的设计变量可写成如下向量形式：

4.3 遗传算法

遗传算法（简称GA）具有全局搜索能力强、鲁棒性强、易于并行化、效率高、解的可靠性高以及遗传函数不一定连续等优点[13-15]而得到广泛应用，因此，这里采用遗传算法对a1和d1尺寸进行选取，遗传算法进化流程图，如图3所示。

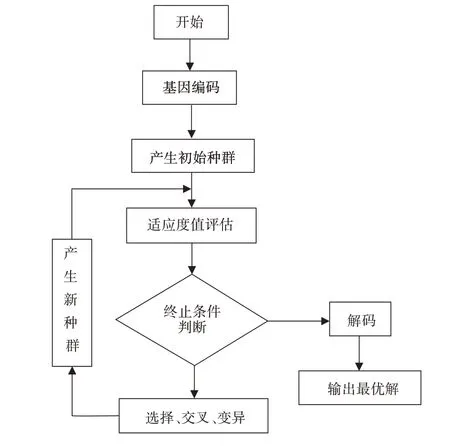
图3 遗传算法流程图Fig.3 Flow Chart of Genetic Algorithm

遗传算法主要由以下内容构成：

（1）基因编码

应用最为广泛的基因编码为二进制编码，其等位基因由（0、1）组成。

（2）适应度函数

由上文知这里的目标优化函数为：

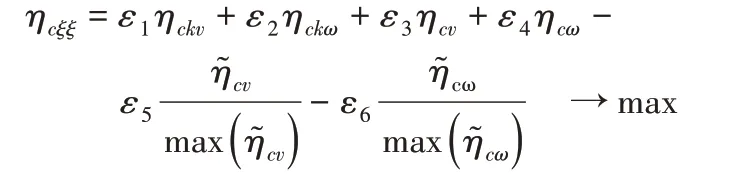
选用单点交叉方法，交叉概率选为0.8，选用变异概率为0.07。

（5）停止准则

根据6R串联机器人整机大体尺寸以及加工装配要求，设主要部件尺寸变化范围为：120cm≤a1≤140cm，120cm≤d1≤140cm，取遗传算法连续两代平均适应度值小于0.001或循环100代作为停止准则。通过遗传算法，最终优化结果为a1=144.999cm，a1=110.0cm，此时，f（x）的最小值为f（x）=-0.541，即全域综合性能评价指标的最大值为ηcξξ=0.541，根据实际需要选取a1=145.0cm，d1=110.0cm，此时机器人各性能指标如表1 所示。6R 串联机构优化前相应指标和结构参数，如表2 所示。优化前，a1=138.0cm，d1=121.0cm，对比表1和表2可以看出，性能指标ηKtv和ηv均得到改善，而性能指标η～v未得到改善，说明各性能指标可能存在互相矛盾的现象，即当一种性能指标较优时，而另一种性能指标可能会变差，即ηcξξ取最大值时，不能满足所有性能指标均为最优。

表1 6R串联机构性能指标优化后结果Tab.1 Optimization Results of Performance Indexes

表2 6R串联机构优化前性能指标值Tab.2 Performance Indexes Value Before Optimization

5 结论

（1）针对串联机器人速度同性指标、灵巧度指标和全域性能波动指标的不足，提出一种串联机器人运动性能的全域综合性能评价指标ηcξξ。

（2）采用单变量分析法，逐个分析了重要结构参数a1和d1对6R 串联机器人全域综合性能评价指标ηcξξ的影响规律，通过分析可知a1值的增大会使机构全域综合性能指标ηcξξ增大，且类似线性规律变化，有利于机构的运动控制；d1值的增大会使6R 串联机构全域综合性能指标ηcξξ减小，不利于机构的平稳运行。

（3）基于遗传算法求得当6R串联机构关键构件尺寸参数为a1=145.0cm，d1=110.0cm 时，全域综合性能评价指标的最大值为ηcξξ=0.541。通过关键尺寸优化前后性能指标对比可看出通过遗传算法优化后，性能指标ηKtv和ηv均得到改善，而性能指标η～v未得到改善，即各性能指标可能存在互相矛盾的现象，即当一种性能指标较优时，而另一种性能指标可能会变差。