振动能量回收装置在电动物流车悬架系统的设计与应用

李 蒙，王 铁，赵 震，王 戎

（太原理工大学机械与运载工程学院，山西 太原 030024）

1 引言

悬架系统是车辆底盘的重要组成部分，在支承车身和吸收振动能量方面起着关键作用[1]。对悬架系统振动能量进行收集，可以为电池充电，提高整车能量利用效率[2]。当前，广大研究者对车辆悬架系统的振动能量收集进行了深入研究。结果表明，采用路面随机高程激励，在不同路面等级下平均回收功率为（40～200）W[3]；典型乘用车在良好的道路上，以97km/h的速度行驶时，回收功率在（100～400）W之间，相当于提高了3%的燃油效率[4]。同时回收功率与振动强度水平有关，簧上质量较大，行驶速度较快，行驶条件较差的车辆具有更好的能量回收应用前景，这在重型卡车和越野车辆的情况下更加明显[5]。在D级路面上，越野车以80km/h的速度行驶时，回收的最大功率可达2048W[6]。

随着压电技术的发展，压电材料越来越多地应用在能量收集领域，同时压电材料具有显著的机电耦合效应，能够有效地进行能量转换。文献[7]通过研究压电悬臂梁发电装置在车身上的安装位置及其工作频率，最大程度利用压电悬臂梁发电装置回收车身振动能量。文献[8]通过改进一种具有多频振动响应的振动能量采集器，提升了压电悬臂梁采集振动能量的能力。文献[9]提出了一种复合L形压电悬臂梁的宽频拓展技术，提高了压电悬臂梁的振动能量采集转换效率。除此之外，文献[10]通过调节压电能量收集装置共振频率与外界激振频率的匹配，提高了回收功率。

以某款轻型电动物流车的前悬架系统为研究对象，设计一种压电能量收集装置，并建立压电发电模型，通过仿真和试验数据对比进行模型验证。结合试验和MATLAB 仿真，讨论并计算不同工况下的发电功率，为今后相关问题的研究提供参考。

2 设计和建模方法

2.1 结构设计和理论建模

四分之一车辆双质量压电收集装置示意图，如图1所示。其中，压电能量回收装置的结构简图，如图1（a）所示。压电陶瓷固定在杠杆的左端和壳体之间，杠杆上有直径4mm的导向固定杆插入到压电陶瓷内孔中，杠杆的右端与钢板弹簧连接架铰接；杠杆的下方通过移动支架进行支撑，移动支架下端和壳体之间安装导轨，在调整螺杆的作用下，移动支架沿导轨左右移动，实现杠杆力臂L1和L2的调整。结构在外界振动源激励下，在杠杆右端施加力的作用，通过调节杠杆力臂调整作用在压电陶瓷上的作用力，以达到最佳的发电效果。

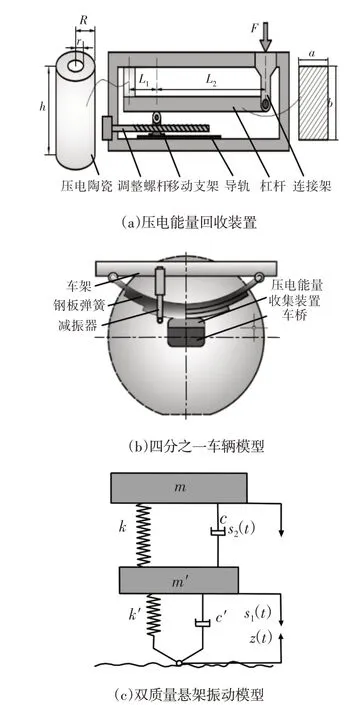
图1 四分之一车辆双质量压电收集装置示意图Fig.1 Sketch of Dual-Mass Piezoelectric Harvester of a Quarter-Vehicle

由于压电陶瓷在一个振动周期中消耗的能量与压电陶瓷产生的能量一致，可得出压电陶瓷阻尼c1，如下式：密度、杆的横截面积和杆的阻尼比。

如图1（b）所示为四分之一车辆模型，压电能量收集装置安装在前悬架钢板弹簧与前桥之间，馈能悬架系统的等效刚度k=k1·k2·k3(k1·k2+k2·k3+k1·k3)，等效阻尼c=c1+c2+c3，k3和c3分别为原悬架系统的刚度和阻尼系数。

根据振动学理论，考虑轮胎阻尼，建立二自由度双质量车辆动力学模型，如图1（c）所示，该模型由簧载质量m、非簧载质量m′、悬架系统刚度k，阻尼c和轮胎刚度k′阻尼c′组成。随机路面不平度z(t)作用到车轮上，引起双质量悬架模型振动，z(t)满足下式：

根据拉格朗日方程，推导出二自由度双质量压电能量收集振动系统的微分方程。如下所示：

式中：s2和s1—簧上质量和非簧上质量相对于它们各自的平衡位置的位移，二自由度双质量压电能量收集振动系统的固有频率为ω1、ω2，振幅比为r1、r2：

系统振动时有阻尼，所受到阻尼力与速度的大小成正比，且速度方向相反。式（3）可以写成下列矩阵形式：

阻尼矩阵可视为质量矩阵与刚度矩阵线性组合的特殊系统，即c=αm+βk。其中，α与β是常数，将阻尼矩阵带入（6）式可得：

将式（12）带入s(t)=Sq(t)，可得到簧载质量和非簧载质量在任意时刻，它们相对于各自平衡位置的位移s2、s1以及速度s˙2、s˙1，簧载质量和非簧载质量的相对位移与相对速度分别为：ti时刻在路面激励的作用下，压电能量回收悬架系统振动，钢板弹簧上变化的力通过杠杆的右端施加到压电陶瓷的极化方向上。

因此，可以获得0到t时刻，压电陶瓷所产生的功率的RMS，如下式所示：

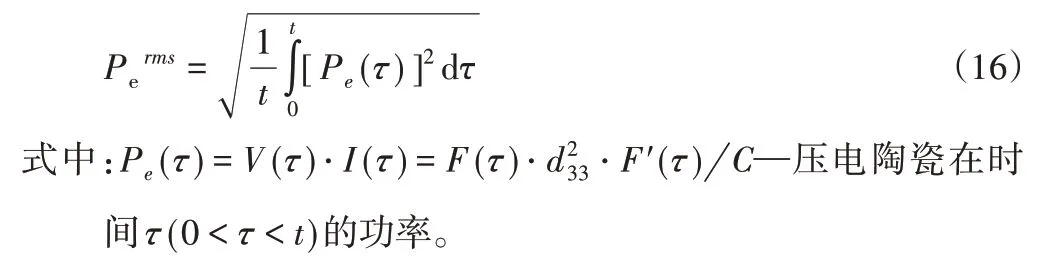
为了计算所产生功率的RMS，可将时间t分成j个时间步长，时间间隔Δt足够短，上式可以用下面的离散形式表示：

2.2 模型验证

为验证前文所建模型的准确性，进行实车试验，B级路面现场试验图，如图2所示。其中，B级随机路面试验，如图2（a）所示。脉冲路面试验，如图2（b）所示。测得车辆空载状态，以20km/h、30km/h、40km/h、50km/h和60km/h的车速行驶在B级路面上，车辆前悬架系统簧上质量的加速度值。运用EEMD（ensemble empirical mode decomposition）方法对采集到的加速度信号进行滤波和降噪处理，提高信号的信噪比。以空载车辆以30km/h速度行驶为例，对馈能悬架簧上质量的加速度信号进行降噪可以得到试验信号的前13阶IMF分量以及残余项RES的计算结果，如图3所示。

图2 现场试验图Fig.2 The Test Site

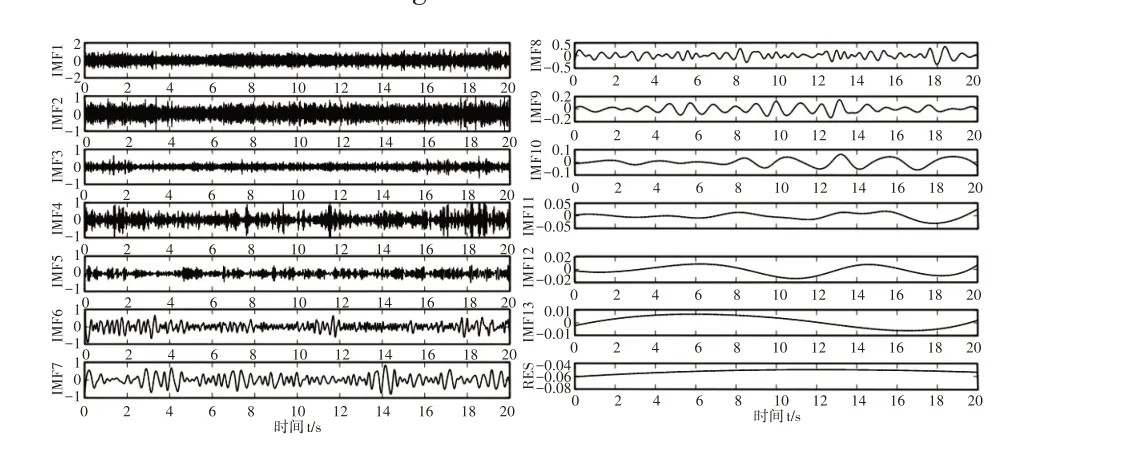
图3 EEMD的分解结果Fig.3 The Partial Decomposition Results of EEMD

根据每阶IMF 的标准差和IMF 与原始信号的相关系数，选取相关的IMF分量进行信号重构。重构信号均方误差越小，表示降噪越有效。相关系数反映重构信号与原始信号的相似程度，其值越大越好。加速度重构信号与原始信号的对比，如图4所示。

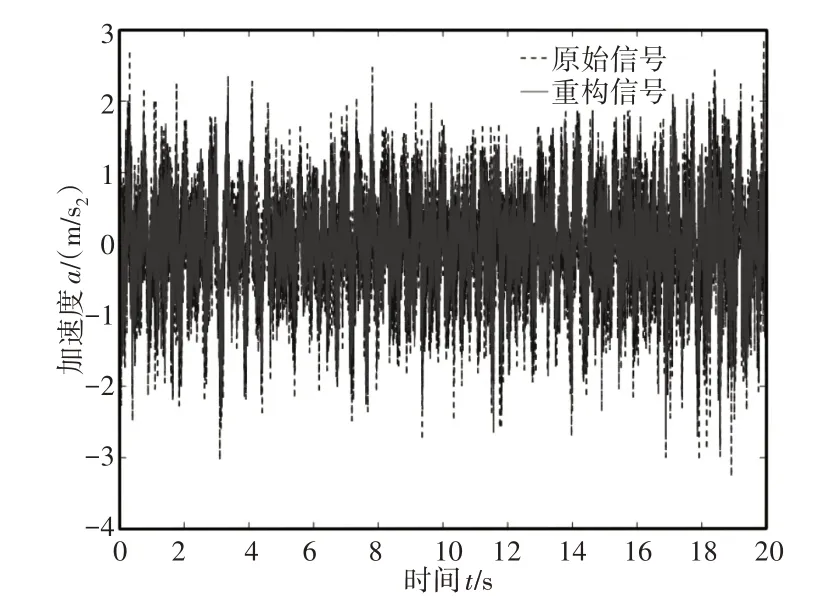
图4 原始信号与重构信号对比Fig.4 The Contrast Between Reconstructed Signal and Original Signal

当空载车辆行驶在B级路面时，不同速度下的路面随机信号可通过式（2）得到，其中，Gq(n0)=64×10-6m3，并可根据表1所列的悬架系统相关参数及双质量压电能量收集悬架系统的振动模型计算出簧载质量在任何时候的加速度值。

表1 馈能悬架系统相关参数Tab.1 The Parameters of Piezoelectric Energy Harvesting Suspension System

为验证振动模型的准确性，表2列出了空载车辆在B级道路上行驶时，不同速度下悬架系统簧上质量加速度均方根值的试验结果和仿真结果之间的比较。

表2 仿真与试验加速度均方根值Tab.2 The Acceleration RMS of Simulation and Test

表中，两组加速度均方根值的变化趋势一致，均随行驶速度的增大而变大，速度为60km/h时，仿真值与试验值出现最大误差13.36%。

对比分析馈能悬架系统簧上质量加速度仿真值与试验值的功率谱密度（PSD）曲线，如图5所示。通过统计学中的统计量拟合优度的可决系数检验模型的精度，进一步说明文中模型建立方法的可行性和有效性，具体如下式：

式中：n—检验模型精度数据的数量；

—第i个模型响应的仿真值；

ai—第i个模型的试验值即真实值；

平均值。

根据图5选取40个样本点来检验模型的精度，得到拟合优度值R2为0.9361，拟合优度值越接近1，说明模型可信度越高。考虑到模型的简化与建立、仿真的计算精度，实际道路路面的平整性、实际测试位置以及驾驶员驾驶技能等因素，认为误差是满足工程实际的，仿真结果符合要求，所建模型是可信的。

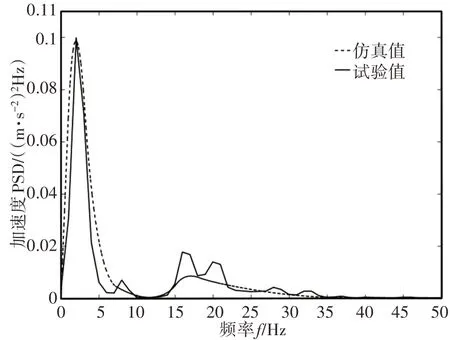
图5 加速度功率谱密度曲线Fig.5 Power Spectral Density of Acceleration

3 结果和讨论

城市电动物流车工作时主要行驶在路况较好的B 级路面上，所以路测试验均在B级路面上进行，现场试验，如图2所示。分别测得车辆空载、满载状态在各种工况下，馈能悬架簧上质量和簧下质量相对速度（s˙21=s˙2-s˙1）和相对位移（s21=s2-s1）。根据试验所得数据，结合式（12）～式（17），可得到在各行驶工况下，馈能悬架系统中压电陶瓷发电功率的均方根值。

3.1 随机路面试验结果及分析

车辆在匀速工况下，车辆行驶速度与载货状态对馈能悬架系统中压电陶瓷发电功率RMS的影响，如图6所示。其中，车速为60km/h时，s˙21和s21随时间变化的曲线，满载时，相对速度最大幅值为0.4578m/s；空载时，相对速度最大振幅为0.2807m/s，如图6（a）、图6（b）所示。图6（c）的结果表明，速度由20km/h 增加到60km/h，空载时发电功率RMS由0.32W增加到5.07W，满载时发电功率RMS由0.35W增加到7.23W。两条曲线的走势一致，发电功率RMS随着速度的增加而增大，且增加速率越来越快。车速为20km/h时，两种载货状态下的发电功率RMS接近，随着速度的增加满载状态的发电功率RMS均大于空载状态下的RMS。

车辆在加速工况下，车辆载货状态对馈能悬架系统中压电陶瓷发电功率RMS的影响，如图7所示。其中图7（a）、图7（b）表示车辆由0km/h均匀加速到80km/h，和随时间的变化曲线，在空载状态下，RMS为1.61W；在满载状态下，RMS为4.47W。空载加速工况下，相对速度和相对位移的幅值均小于满载加速时；满载时最大相对速度幅值为0.5198m/s，最大相对位移幅值为0.01251m。对比图7（a）、图7（b）和图6（a）、图6（b）中的曲线发现，在相同载货和速度状态下，加速过程中和的幅值均小于匀速行驶时的幅值。主要原因是在加速度的作用下，在加速过程中前轴所受的垂直载荷比匀速行驶时所受的载荷小。

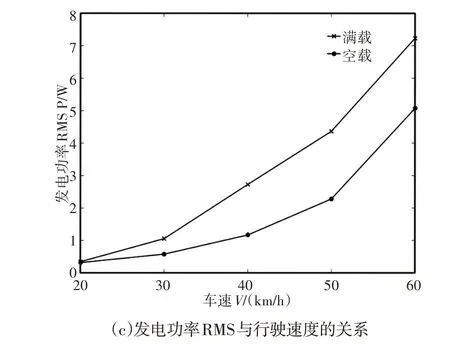
图6 随机路面激励下，相对速度、相对位移和功率RMSFig.6 Relative Velocity，Relative Displacement and RMS of Electric Power Base on Random Road

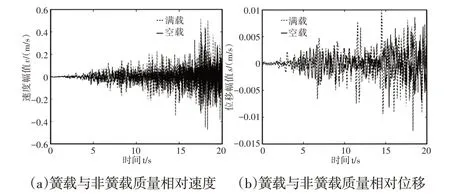
图7 加速期间的相对速度与相对位移Fig.7 Relative Velocity and Relative Displacement During Acceleration Process

3.2 脉冲路面试验结果及分析

城市电动物流车在行驶过程中，会经常遇到减速块，如图2（b）所示，试验时车辆分别以10km/h、20km/h、30km/h 和40km/h的速度通过两组间距为20m的减速块，采样时间均为10s。

车辆在脉冲路面行驶时车速和载货状态对馈能悬架系统中压电陶瓷发电功率RMS的影响，如图8所示。车辆在空载和满载状态下，以30km/h的速度通过减速块时，馈能悬架簧上质量和簧下质量相对速度s˙21和相对位移s21的幅值变化情况，如图8（a）～图8（d）所示。空载时相对速度s˙21和相对位移s21的最大幅值分别为2.493m/s和0.05858m，满载时相对速度s˙21和相对位移s21的最大幅值分别为2.473m/s和0.0536m。车辆在空载和满载状态下的压电能量收集装置发电功率RMS，最大值均出现在以30km/h的速度通过减速块时，最大值分别为102.24W 和88.09W，如图8（e）所示。两条曲线的变化趋势基本一致，速度由10km/h变化到30km/h时，发电功率RMS增大；速度由30km/h增大到40km/h时，发电功率RMS减小。这是因为车速为30km/h通过脉冲输入路面时，产生的振动频率接近车辆自身的固有频率，车辆此时的振动最大。

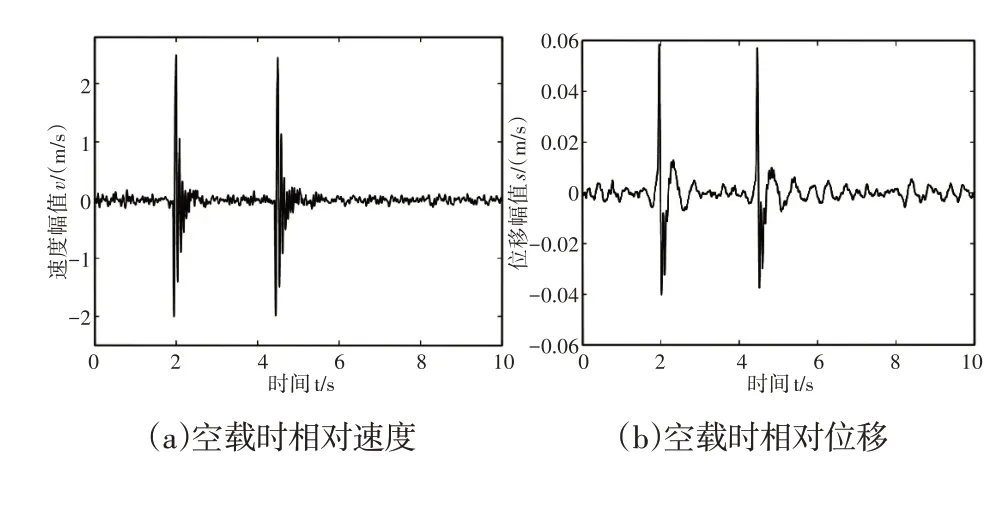
图8 脉冲路面激励下，相对速度、相对位移和功率RMSFig.8 Relative Velocity，Relative Displacement and RMS of Electric Power Base on Pulse Road

在各个车速下，车辆空载状态下的发电功率RMS值均比满载时的发电功率RMS值大，这是由于满载后增加了簧上质量，提高了馈能悬架系统的振动性能。

4 结论

（1）这里设计了一种制造安装方便的压电能量收集装置，该装置可通过调节杠杆力臂比调整施加在压电陶瓷上的激振力，从而提高能量收集装置所产生的发电功率，为压电能量回收提供了新思路。（2）建立了四分之一车辆馈能悬架系统振动模型，并进行随机路面试验，通过对比试验数据和仿真数据，并进行拟合优度计算，验证了模型的准确性，说明了理论分析的合理性，为振动模型的仿真分析提供了基础（3）通过试验与仿真分析，讨论了影响发电功率的工况因素，结果表明在随机路面输入下，发电功率均方根值与车辆行驶速度载货状态成正比，为压电能量收集装置的应用与优化提供了依据。（4）预期在实践中，可以在车辆上安装四个或更多压电能量采集器，以从车辆悬架系统的振动中收集有效和实用的能量，作为车辆的辅助能量源，这为使用压电技术收集悬架系统的振动能量提供了有力的参考。