冲击载荷下不同含水率砂岩动力学特性试验研究

赵恕轲，赵明诚，杨伟玮，

(1.山东省调水工程运行维护中心平度管理站，山东 平度 266700；2.西安科技大学建筑与土木工程学院，陕西 西安 410083)

0 引 言

天然矿物结合体内部包含大量的原生裂隙和次生裂隙，富水环境中的岩体受到地下水渗透作用的影响，水-岩作用导致岩体节理面的力学特性显著降低，进而加剧岩体强度发生劣化。岩体工程经常伴随着机械及爆破开挖等作用引起的岩体活动[1-2]，导致岩体应力环境发生变化，使岩体处于力学扰动环境中[3- 4]，水-岩劣化导致岩体发生失稳破坏。水-岩劣化现象一直备受水利工程领域关注，特别是导流渠及输水管道岩体水-岩耦合作用下的岩体稳定性及强度劣化关系到工程的安全运营。岩体开挖过程中，机械钻凿开挖强度的增强实则提高了冲击波的输入强度，冲击荷载扰动作用也极易导致富水围岩体发生失稳，对岩体的安全运营机制产生影响[5-7]，许多学者对不同含水率岩体进行动力学试验研究。袁璞等[8-9]采用动静组合加载试验装置研究岩石动态力学性能与含水率的相关性发现，自由水的表面张力和Stefan效应抑制了裂纹动态扩展，而裂纹扩展阻力、动态强度与含水率呈正相关；Friedman等[10]基于动力学试验测试水-岩作用下灰岩动力学性能表明，抗冲击强度与含水率呈负相关，而破碎程度与含水率呈负相关，饱水动态强度相比干燥状态降低了35%；楼沩涛[11]利用动静组合加载装置对花岗岩进行的动力应变试验研究表明，加载速率对饱和花岗岩的抗拉强度具有显著影响；Huang等[12]研究了动静组合加载条件下砂岩抗拉力学参数与含水状态的相关性；谢晓锋等[13]研究发现，岩石的动态和静态应力-应变曲线具有显著性差异，岩样峰值强度、弹性模量随饱和时间增大而降低。

以上研究更多关注人为饱和岩石试样的动态力学特性，对实际开挖岩体的自然含水率对其力学特性的影响研究较少涉及。为此，本文以山东平度市大泽山砂岩为试验材料，基于改装的分离式霍普金森压杆(SHPB)，对不同含水状态的砂岩试样进行动态力学试验，测得动态应力-应变曲线，研究自然含水率对动态应力-应变特征、动态峰值应力、动态峰值应变、动态弹性模量以及砂岩微观特性的影响规律。

1 试验材料及装置

1.1 砂岩试样

砂岩取自山东省平度市大泽山镇，主要矿物为石英、氧化铁及少量黏土矿物，呈红褐色，细观颗粒分布均匀、无明显裂隙，见图1。为研究含水率对砂岩动态力学特性的影响，在现场先切取5种不同含水率的30 cm×30 cm×30 cm立方体岩块，密封保存后带回试验室。试验假定临近岩样具有相同含水率，每种含水率岩体制取6个标准试样；取样时两两临近，3个用于测试含水率，3个用于力学试验。基于Davies和Hunter研究结果并考虑试验装置的入射杆直径(Φ=50 mm)，将试样制作成直径约50 mm、高约50 mm的圆柱体。为避免入射杆-试样界面产生应力集中，通过磨石机对试样端面打磨，使其平整度≤0.05 mm。

将试样置于烘干机并于常温下风干48 h，通过试样质量差计算岩样含水率，平均含水率ω为0.75%、1.39%、2.57%、3.89%和5.62%。对备用试样进行测试，砂岩粒径为0.05～2.26 mm，密度为2.33～3.68 g/cm3，孔隙度为2.88%～5.36%。

1.2 试验装置及原理

试验在西安科技大学动力学试验室的改进式分离霍普金森压杆上完成。试验系统由冲击加载装置、轴压加载装置及数据采集设备构成。冲击杆、入射杆、透射杆以及缓冲杆材料为40Cr合金钢，密度为7 810 kg/m3，弹性模量为250 GPa，满足试验要求。应力波采集及显示装置分别为2021AS超动态应变仪(灵敏度为1 mV/με)、855E型示波仪(采集分辨率为10 bit/D，显示频率阈值设置为0.01 Hz)。岩样冲击速度由激光测速仪测试。试验过程中，冲击杆的撞击强度由动力加载装置(高压气体)提供，应力波传播路径为入射杆-砂岩-透射杆。透射杆和入射杆上的应变片可捕捉透射波、入射波(反射波)，最终显示在示波器上。试验装置见图2。

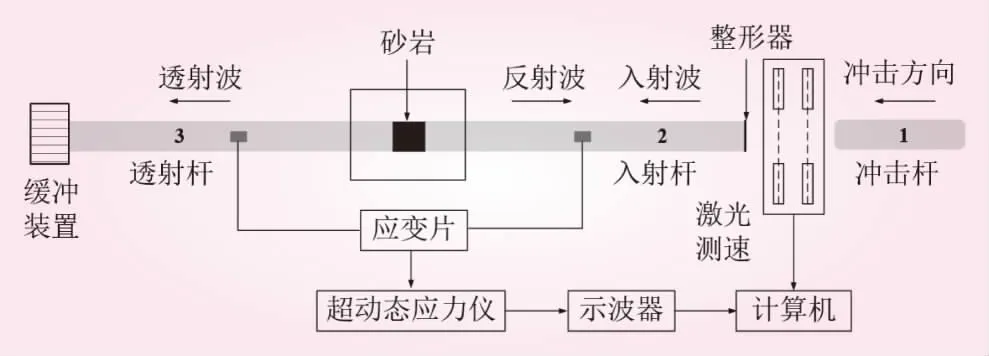
图2 试验装置

根据一维应力波理论，入射应力σI(t)、反射应力σR(t)和透射应力σT(t)间关系表示为[13]

σ(t)=Ae[σI(t)+σR(t)+σT(t)]/2As

(1)

砂岩应变ε(t)为

(2)

根据应力均匀性假定，入射应力、反射应力及透射应力的等效关系为

σI(t)+σR(t)=σT(t)

(3)

平均应力和应变分别表示为

σ(t)=σT(t)Ae/As

(4)

(5)

式中，As和Ae分别为砂岩、弹性杆(入射杆和透射杆)的有效截面面积；L为岩样高度；ρe和Ce分别为弹性杆的密度及波速。

1.3 试验方案

按照试验方案，相同冲击强度下，不同含水率砂岩的动力学试验步骤如下：①调试SHPB装置，确保入射杆、透射杆和缓冲杆满足“三杆一线”，高压气体强度为0.25 MPa(冲击速度约为1.50 m/s)，进行尝试性试验以保证数据采集正常。②按照平均含水率分别为0.75%、1.39%、2.57%、3.89%和5.62%，将砂岩编号为R-1～R-15，将试样放置于入射杆和透射杆中间，涂抹适量耦合剂，并确保试样中心轴与入射杆、透射杆的中心轴处于同一水平线。③安装防爆容器，防止碎岩块飞溅伤人。

2 试验结果

根据试验方案，依次对含水率为0.71%～0.78%(R-1～R-3)、1.36%～1.38%(R- 4～R- 6)、2.44%～2.67%(R-7～R-9)、3.64%～4.15%(R-10～R-12)、5.50%～5.72%(R-13～R-15)的砂岩试样进行冲击速度约为1.50 m/s的冲击试验，获得动态应力-应变曲线。不同含水率ω砂岩的动态峰值应力σd、动态峰值应变εd、动态弹性模量Ed以及实际冲击速度Vd见表1。从表1可知，随着含水率的增大，动态峰值应力、动态峰值应变和动态弹性模量均逐渐减小，这与王文等[14]研究结果一致。由于数据较多，图3仅给出不同含水率状态下(0.75%、1.38%、2.59%、3.88%、5.64%)部分典型砂岩的动态应力-应变关系。

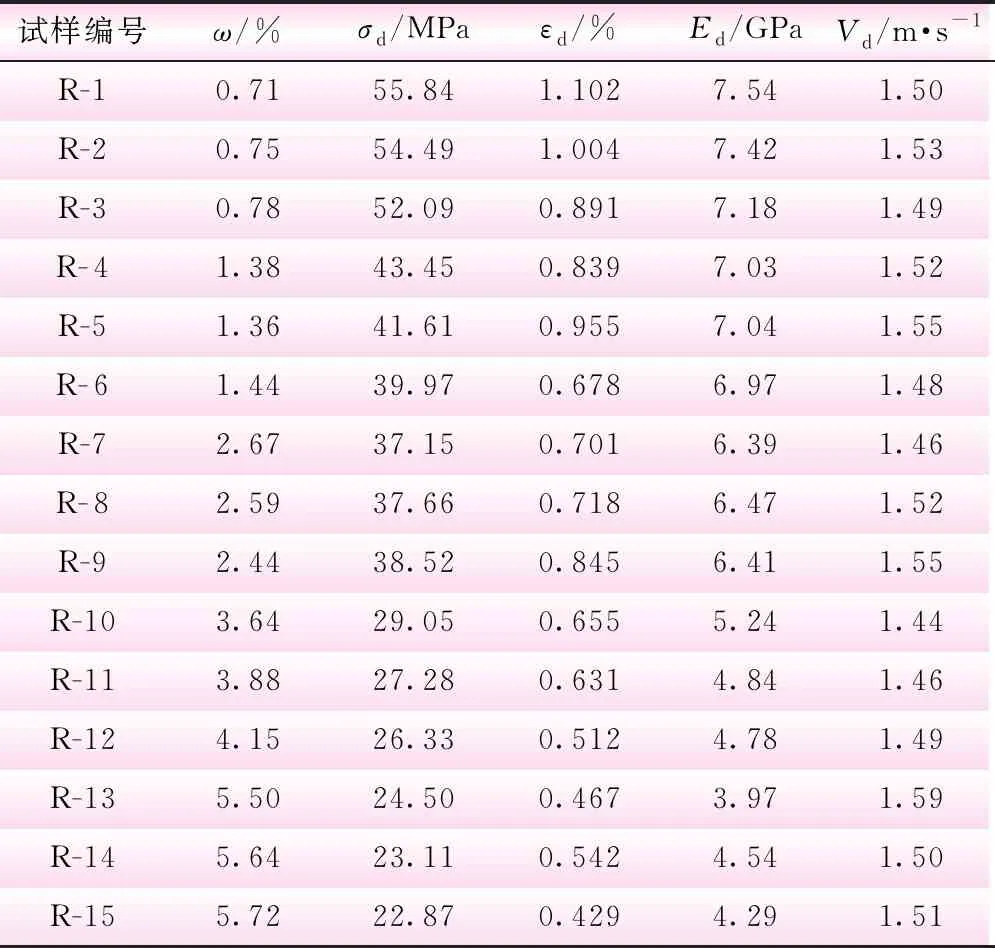
表1 砂岩的动态力学参数

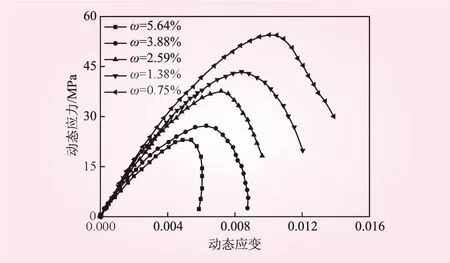
图3 砂岩动态应力-应变关系

3 讨论与分析

3.1 动态应力-应变曲线形态特征

从图3可以看出，砂岩动态应力-应变曲线与静态应力-应变具有显著性差异，即动态应力-应变曲线未出现明显压密变形而直接发生弹性变形；随着岩样应变程度的增加，动态应力-应变曲线依次进入损伤变形和破坏变形阶段。分析原因认为，高强度冲击作用下，岩样内部产生了瞬态变形，岩样未来得及被压缩密实而快速发生弹性变形[15]，进而动态应力-应变曲线未出现压密阶段。对比发现，①砂岩含水率对动态弹性变形阶段具有显著影响，弹性变形阶段的线性斜率与含水率呈负相关，砂岩含水率越大，弹性模量越小。②砂岩含水率对动态应力-应变的演化路径具有显著影响，随着含水率的增大，应力-应变曲线路径相对缩短，峰值应力及应变明显降低。

此外，砂岩由弹性变形到塑性变形的演化特征与静态应力-应变曲线具有一致性，动态应力-应变曲线演化过程包括线弹性、弹塑性和塑性软化3个阶段[15]。当应力达到80%动态峰值应力时，动态应力-应变曲线的上升趋势开始逐渐减缓随后下降，这与文献[16-17]结果一致。

3.2 砂岩动力学参数特征

3.2.1 动态峰值应力规律

从表1可知，砂岩含水率为0.71%～0.78%时，其动态峰值应力为52.09～55.84 MPa，抗冲击能力最大；相比含水率为0.71%～0.78%的平均动态峰值应力，含水率为1.36%～1.38%、2.44%～2.67%、3.64%～4.15%和5.50%～5.72%的平均动态峰值应力分别为41.68、37.78、27.55 MPa和23.49 MPa，降低了23.01%、30.22%、49.11%和56.61%，衰减程度显著增大。砂岩动态峰值应力与含水率的对应关系见图4。从图4可知，含水率为1.38%相比0.75%的平均动态峰值应力降低了23.01%，含水率为2.59%相比1.38%的平均动态峰值应力降低了9.36%；含水率为3.88%相比2.59%的平均动态峰值应力降低了27.08%；含水率为5.64%相比3.88%的平均动态峰值应力降低了14.73%。平均动态峰值应力随着含水率增加总体呈一阶指数函数变化，相关系数R2为0.964 3。因此，砂岩的动态峰值应力的变化曲线随含水率增大逐渐减缓，渗透水对不同位置的砂岩的软化损伤作用具有差异性。

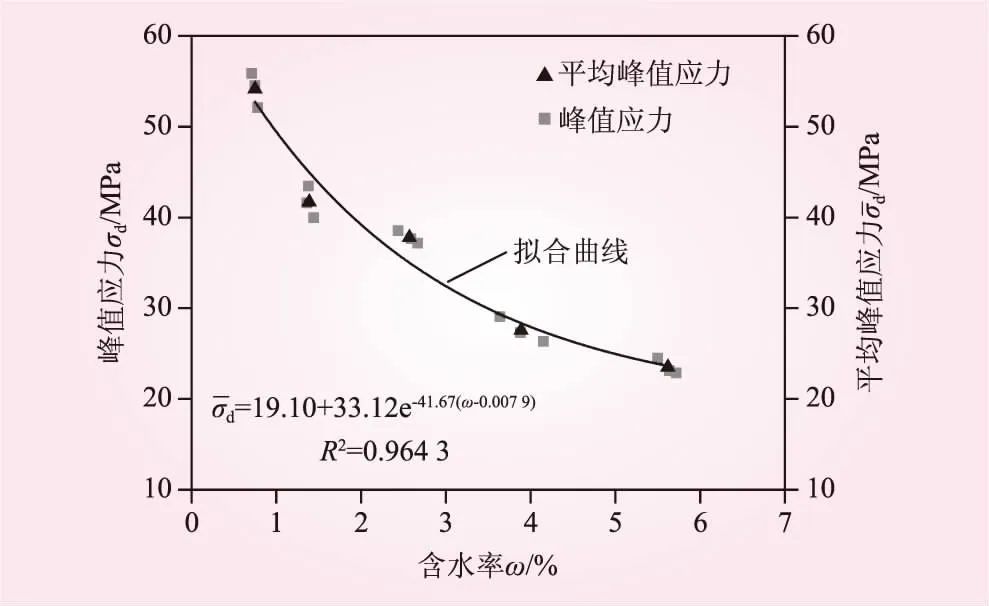
图4 动态峰值应力与含水率的对应关系

3.2.2 动态弹性模量分析

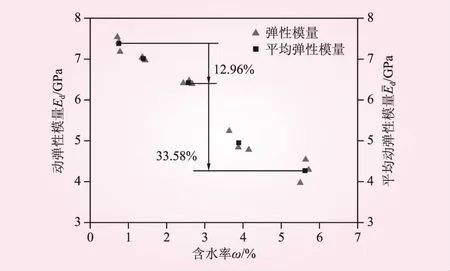
图5 动态弹性模量与含水率的对应关系

3.2.3 动态峰值应变分析

砂岩动态峰值应变与峰值应力具有相似发展趋势，均随含水率的增大而减小。当含水率由0.71%～0.78%分别增大到1.36%～1.38%、2.44%～2.67%、3.64%～4.15%和5.50%～5.72%时，砂岩平均动态峰值应变分别为0.008 24、0.007 55、0.005 99和0.003 51，降低了17.52%、24.46%、40.01%、64.90%。由此可见，动态峰值应变在含水率为2.44%～2.67%时的降低程度显著增大，表明砂岩含水率大于2.44%～2.67%时内部增加的损伤将快速降低其抗冲击能力，进而加快岩样破裂。研究还发现，动态峰值应变快速减小的平均含水率分界点与图5中动态弹性模量的平均含水率分界点相同，均为2.56%。图6为动态峰值应变与含水率的对应关系。从图6可知，相同冲击强度下，不同含水率下的动态峰值应变总体呈缓慢减小的发展趋势。回归数据发现，平均动态峰值应变与含水率呈指数函数关系，这与詹金武等[18]对冲击荷载作用下泥质粉砂岩的应变特性研究成果一致。

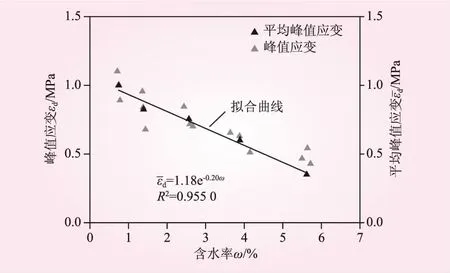
图6 动态峰值应变与含水率的对应关系

3.3 砂岩微观力学特性分析

3.3.1 单位质量进汞体积曲线

图7为不同含水率砂岩单位质量进汞体积曲线。从图7可知，随着孔径的增大，不同含水率的砂岩单位质量进汞体积均经历了先急剧增加(A区域，见图8)、后平稳发展、最后持续增加3个发展阶段，孔径的分界点大致为1.50×103nm和22.50×103nm。当孔径≤1.50×103nm时，砂岩中以小尺寸孔隙为主，较小含水率下的孔隙先达到饱和，单位质量进汞体积先进入平稳发展阶段；当孔径≥1.50×103nm而<22.50×103nm时，砂岩中以中型孔隙为主，单位质量进汞体积显著增大；当孔径≥22.50×103nm时，砂岩中大尺寸孔隙逐渐占据优势，单位质量进汞体积曲线持续增大。这说明砂岩的内部溶蚀(损伤)程度对含水率具有不同敏感性。

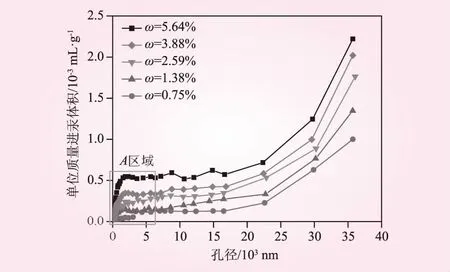
图7 不同含水率砂岩单位质量进汞体积曲线

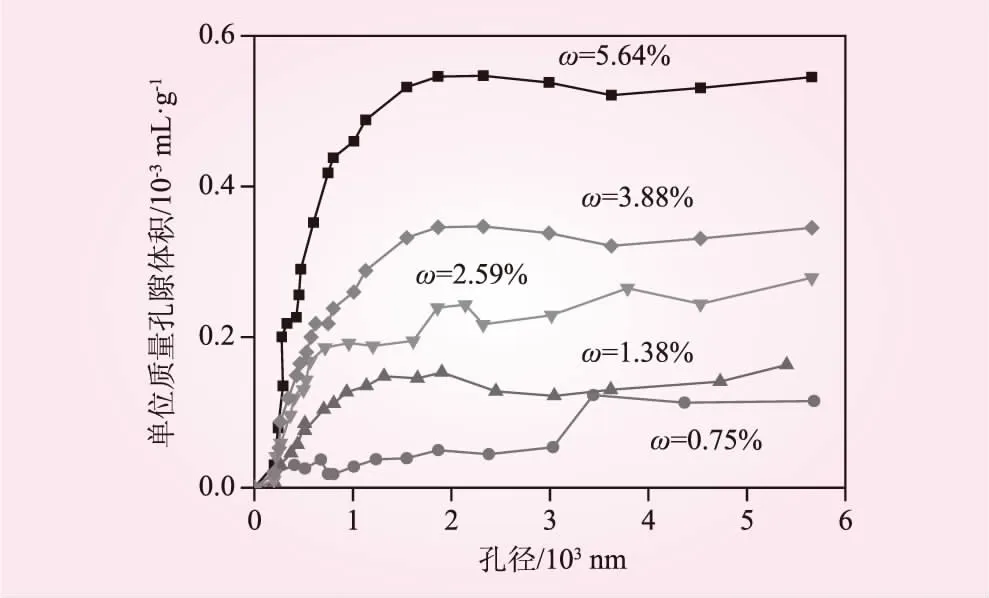
图8 急剧增长阶段发展趋势

从图7还可以看出，同一孔径下，含水率越大，砂岩的单位质量进汞体积越大，这表明增大的含水率显著加剧了砂岩的溶蚀程度。含水率对单位质量进汞体积的初期增长具有显著影响，含水率越大，曲线增长越显著，增长路径越长。分析认为，对于富水岩体，地下水对岩体内部结构面具有显著润滑与溶蚀作用。地下水通过原生孔裂隙、节理深入岩体结构内部后，渗透水可在矿物表面形成润滑水膜，导致岩体结构摩擦力和稳定性显著降低。此外，受到地应力作用影响，地下水往往具有一定渗透压，高压渗透水可加快原生孔隙的张开与贯通程度，加剧内部新生裂隙的生成，导致岩石骨架上矿物粒子迅速剥离成游离状态，最终加剧岩体溶蚀程度。

3.3.2 累积单位质量孔隙体积

以单位质量孔隙体积曲线达到最大发展阶段时对应的累积单位质量孔隙体积衡量砂岩的微观孔隙分布特征。砂岩累积单位质量孔隙体积与含水率关系见图9。从图9可知，砂岩含水率由0.75%增大到1.38%时，累积单位质量孔隙体积提高了53.51%；含水率由1.38%增大到2.59%时，累积单位质量孔隙体积提高了43.98%；含水率由2.59%增大到3.88%时，累积单位质量孔隙体积提高了38.21%；含水率由3.88%增大到5.64%时，累积单位质量孔隙体积提高了39.63%。随着含水率的增大，累积单位质量孔隙体积总体呈增加趋势，增长趋势逐渐趋于平缓且增长速率逐渐减小，说明累积单位质量孔隙体积对含水率的敏感性逐渐减缓，这与赵建平等[19]研究结果一致。回归分析发现，砂岩的累积单位质量孔隙体积与含水率呈较好的对数函数关系。

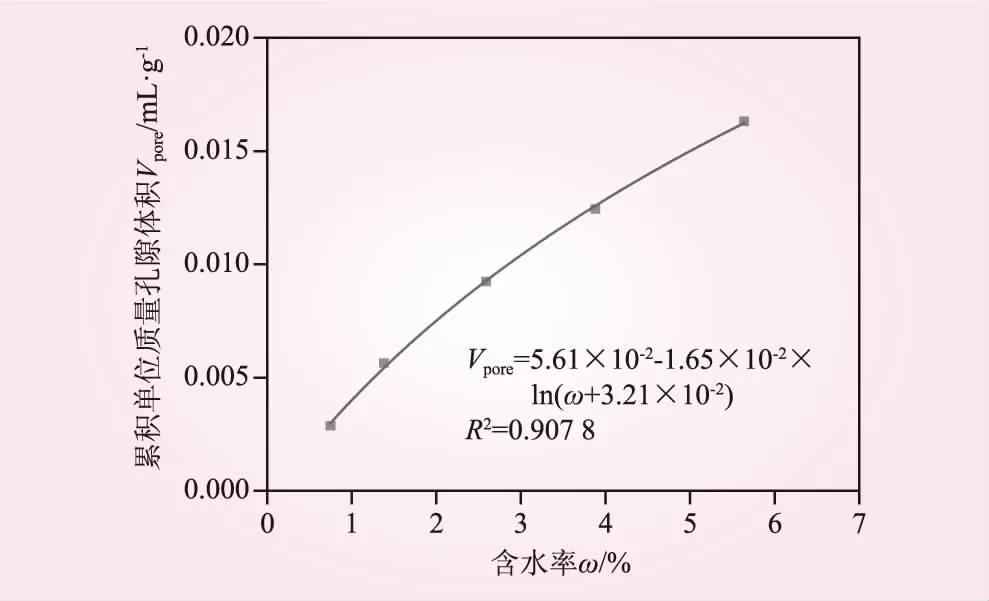
图9 累积单位质量孔隙体积与含水率关系

3.3.3 孔隙体积比演化规律

为研究不同含水率对砂岩中大、中、小孔隙变化趋势的影响程度，定义某一含水率下的孔隙体积比β为

(6)

式中，Vpore为某一含水率下的大孔隙体积Vb、中孔隙体积Vm、小孔隙体积Vs；Vtotal为某一含水率下的累积孔隙体积。

不同含水率砂岩的大、中、小孔隙体积比的变化趋势见图10。从图10可知，随着含水率的增大，砂岩大、中、小孔隙体积比变化范围分别为22.65%～36.88%、43.08%～45.29%和9.01%～34.25%。可见，含水率对大、中、小孔隙体积比的变化趋势具有显著影响。随着含水率的增大，大孔隙体积比总体呈减小趋势，而小孔隙体积比总体呈增长趋势，可见小孔隙体积对含水率的敏感程度显著大于大孔隙体积；随着含水率的增大，中孔隙体积比总体呈缓慢的稳态发展，表明中孔隙对含水率增加的敏感程度较小，这与前人研究具有一致性。砂岩的大、中、小孔隙体积比随含水率的增大总体呈线性变化。

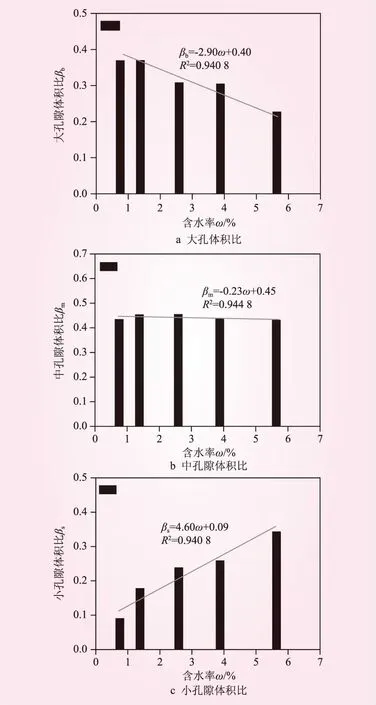
图10 不同含水率砂岩的孔隙体积比变化趋势

分析原因认为，岩石内部含水率增大时，地下渗透水对岩石孔隙内游离态粒子具有显著的冲刷、疏通作用，特别是在具有渗透压作用的富水岩体区域，这种水-岩相互作用更为明显[20]。因此，本试验中增大的含水率导致砂岩内部的原生单一孔隙逐渐向多孔隙结构体演化，导致其单位质量的孔隙体积增大；增大的含水率还会促进砂岩内孔隙的溶蚀与贯通，导致孔隙的孔候尺寸变大，增大渗透水与岩石结构面的接触面积，加剧渗透水的溶蚀深度。

4 结 语

本文基于改装的分离式霍普金森压杆(SHPB)对大泽山砂岩进行了不同含水率下的冲击动力学试验，分析不同含水率砂岩的动态力学特征，并根据压汞试验研究砂岩微观力学特性，得出以下结论：

(1)砂岩动态应力-应变曲线未经历明显压密变形而直接发生弹性变形，应变演化路径与含水率呈负相关，弹性变形及塑性变形的转折点大致为峰值应变的80%。相同冲击强度下，砂岩含水率越大，力学特性劣化效果越显著，抗冲击能力越差。动态峰值应力和弹性模量随着含水率的增大分别呈指数和对数函数衰减。

(2)砂岩溶蚀程度对含水率具有不同敏感性。单位质量进汞体积呈急剧增加、平稳发展、持续增加变化，孔径分界点大致为1.50×103nm和22.50×103nm。累积单位质量孔隙体积随含水率的增大呈对数函数增加。

(3)含水率对大、小孔隙体积比的影响较为明显而对中孔隙体积比的影响不明显；大、小孔隙体积比随含水率的增大分别呈线性衰减、线性增大，而中孔隙体积比变化相对不显著。