基于自适应扩展Kalman滤波的路侧多传感器融合

武一民，郑凯元,2，高博麟，陈 明,2，王义锋

（1. 河北工业大学 机械工程学院，天津300130，中国；2. 清华大学 车辆与运载学院，北京100084，中国；3. 滴滴出行，北京100089，中国）

借着人工智能、云计算、大数据等新一轮的科技革命，自动驾驶技术不断发展与完善，其中准确、全面的环境感知技术是自动驾驶汽车决策与控制的前提，是行驶安全的保障[1]。传感器是感知外界环境的强有力手段，目前车载端传感器感知视野有限、测量稳定性差、成本相对较高；而路侧端传感器探测范围广、安装平台稳定[2]。相机(cameras)、激光雷达(lidars)、毫米波雷达(radars)等单一传感器，各有优缺点，不能独自胜任自动驾驶环境感知任务；为了充分利用不同传感器的特点，实现优势互补，需要进行多传感器信息融合[3]。路侧多传感器信息融合能准确提供动静态障碍物信息，对提高自动驾驶汽车的行驶性能具有重要意义。

按照数据的抽象层次不同，多传感器信息融合方法可分为4类[4]：数据级（像素级）融合、特征级融合、目标级融合[5]、决策级融合。其中数据级融合与特征级融合通常称为前融合，目标级融合与决策级融合称为后融合。

传统估计理论为多传感器信息融合技术奠定了良好的基础，主要包括Bayes理论[6]、粒子滤波[7]、Kalman滤波[8]、证据理论等[9]。其中以Kalman滤波原理为基础的各类算法在多传感器信息融合领域得到了广泛的应用。为了提高基于多传感器融合的目标状态估计的精度，研究者们提出了多种融合策略和滤波算法改进方案。黄文锦等人利用车载激光雷达和路侧双目摄像头，提出了一种基于Kalman滤波的位姿信息融合算法[10]，通过时空同步、数据关联、双层信息融合完成了对自身位姿的估计。由于机动目标是一个非线性系统，而经典Kalman滤波只能处理线性系统[11]。黄彬等人利用车端的相机、毫米波雷达、激光雷达采集到的车辆前方目标物信息[12]，提出了基于扩展Kalman滤波的信息融合算法；为了获取传感器误差特性，给Kalman滤波算法设置合理的量测噪声，该研究利用动静态实验获取了传感器的动静态感知性能，建立了动静态下的传感器感知误差模型。但此种实验手段仅适用于车载端传感器，路侧端传感器的融合方法亟需探索突破。

由于目标远近等客观因素的影响，传感器的感知稳定性差，量测噪声是动态变化的。传统扩展Kalman滤波（extended Kalman filter, EKF)与无迹Kalman滤波(unscented Kalman filter, UKF)算法中，量测噪声协方差矩阵是恒定的，导致融合结果难以动态适应传感器变化特性。针对此类问题，王向华等人提出了一种自适应Kalman滤波算法[13]，通过同一时刻2次不同步长的Kalman滤波结果，自适应的调整量测噪声协方差矩阵，降低了由于量测噪声不准确造成的精度损失。然而在不同的应用背景下，对量测噪声进行调整仍是十分棘手的问题。

针对路侧多传感器融合过程中的传感器误差特性难以在线获取且动态定量描述的问题，本文提出一种基于自适应扩展Kalman滤波器的路侧多传感器融合方法。通过多项式拟合的方式求取各传感器测量值序列的残差，通过方差函数生成初始化量测噪声；通过对传感器测量值稳定性进行检测，生成量测噪声的修正系数，对其进行自适应调整；采用扩展Kalman滤波算法对多传感器信息进行融合。经实车试验，以验证所提方法的有效性。

1 基于自适应扩展Kalman滤波的多传感器融合算法

1.1 路侧多传感器融合框架

路侧多传感器融合框架如图1所示。传感器包含相机、毫米波雷达、激光雷达3种。各传感器通过自带的检测跟踪算法，输出交通参与者的目标级数据，其中包含：时间戳、目标类型、空间位置、速度、加速度、角速度等。由于各传感器的起始时间和数据更新频率不同，在进行融合之前，需对传感器信息进行时间同步，假设一个周期内目标运动属性的变化是线性的，采用线性插值[14]的方式进行时间同步，即利用传感器连续2个时刻的数据，通过插值计算出某一时刻的等效数据。在空间上，所有传感器的目标级数据均已转换到了通用横Mercator格网系统（universal transverse Mercator grid system，UTM）坐标系下。经过时空同步的目标级数据传递到边缘云信息融合平台，再通过本文提出的自适应扩展Kalman滤波算法，对多传感器信息进行融合。

1.2 状态量定义

目标车辆行驶在开放性道路上，需对车辆的状态进行观测，而车辆、行人、非机动车等交通参与者的加速度和角速度在短时间（例如不超过一个采样周期）内近似不变[15]，故采用常角速度常加速度（constant turn rate and acceleration，CTRA)模型来描述目标的运动变化。

令目标的状态向量为

其中：x和y分别表示目标车辆位于UTM坐标系下的绝对横向距离和纵向距离；vx和vy分别表示目标车辆位于UTM坐标系下的绝对横向速度和纵向速度，由合速度v分解得到；ax和ay分别表示目标车辆位于UTM坐标系下的绝对横向加速度和纵向加速度；ω为目标车辆的角速度。

1.3 AEKF融合算法流程

由于传感器的量测噪声会随着运动目标的位置、状态的不同而动态变化，采用定噪声值，易造成滤波不稳定甚至发散，故以扩展Kalman滤波为基础，利用修正系数自适应调整量测噪声协方差矩阵，对EKF算法进行优化改进。AEKF融合算法流程如下：

1） 采用CTRA模型，建立系统状态转移方程。若令T为时间步长，则各状态向量分量的转移公式为：

根据上述状态转移方程，求解状态转移矩阵的Jacobi矩阵Fk。

2） 时间更新阶段。由第一步计算得到的Jacobi矩阵Fk对目标状态xk及状态协方差矩阵Pk进行预测。

3） 确定观测矩阵。采用量测融合的方式对多传感器信息进行融合，如图2所示，量测融合[16]即将所有传感器的测量值以向量的形式组合起来，然后进行滤波。

令量测向量z= [zc,zr,zl]T,其中zc= [xc,yc,vcx,vcy,acx,acy,ωc]T为路侧相机的量测向量，zr、zl同理，分别为路侧毫米波雷达和激光雷达的量测向量，角标c、r、l分别代表相机(camera)、毫米波雷达(millimetre wave radar，或者radar)、激光雷达(laser radar，或者lidar)。根据状态向量x和量测向量z确定观测矩阵H=E7，其中H是状态向量x和量测向量z的映射矩阵，本文为7阶单位阵E7。

3）求解量测噪声。本文通过处理一定时间序列的传感器的测量值，进而求解量测噪声。对传感器一定时间序列的测量值进行拟合，得到不同传感器各种测量值的拟合项：

其中：zik为量测向量z的第i个分量在时间k内的测量值序列，ẑik为量测向量z的第i个分量在时间k内的测量值序列的拟合项，fitf(·)为拟合函数，可为多项式、样条函数、三角函数等。

量测向量z的第i个分量在时间k内的测量值序列的残差为

通过方差函数，计算传感器的量测噪声。

k时刻第i个分量的初始化量测噪声为k时刻的初始化量测噪声矩阵为

R0k会随着时间的增加不断收敛稳定。

4） 量测噪声的自适应调整。考虑到目标运动状态的不确定性以及传感器的动态感知特性，系统中的量测噪声是动态变化的，为保证滤波稳定，通过定义修正系数u，对量测噪声进行动态调整。首先通过对传感器测量值的稳定性进行检测，生成修正系数。k时刻第i个量测分量的修正系数为

其中：zik为k时刻第i个量测分量的测量值，ẑki为k时刻第i个量测分量的拟合值，δi为第i个量测分量的阈值。反应测量值的波动性，可以是常量或时变函数，本文将传感器测量值的波动性约束在一个固定值内，故采用常量δi，δi的数值选取用Δzik绝对值的百分位数来确定，将一段时间内的Δzik的绝对值从小到大排列，选择其合适的百分位数作为δi，将传感器测量值的波动性约束在一个较小的范围内。若k时刻第i个测量值的残差zik-ẑki小于等于δi，表明传感器的测量值稳定，则设定第i个量测分量的修正系数uki等于1；若k时刻测量值的残差zki-ẑik大于δi，表明传感器的测量值不稳定，则设定uki为大于1的值，用以放大该量测分量的噪声方差。

构造量测噪声修正矩阵为

利用Nk对初始化量测噪声矩阵R0k进行自适应调整，得到新的量测噪声矩阵为

2 试验验证

为验证所提路侧多传感器融合方法的有效性，在某丁字路口部署了3个传感器：相机、毫米波雷达、激光雷达。相机采用的是 200 万像素，分辨率为 1 920× 1 080 的工业用途专用相机。激光雷达采用的是Velodyne HDL-64E激光雷达。毫米波雷达采用的是77 GHz的交通检测雷达。各传感器的精度如表1所示。

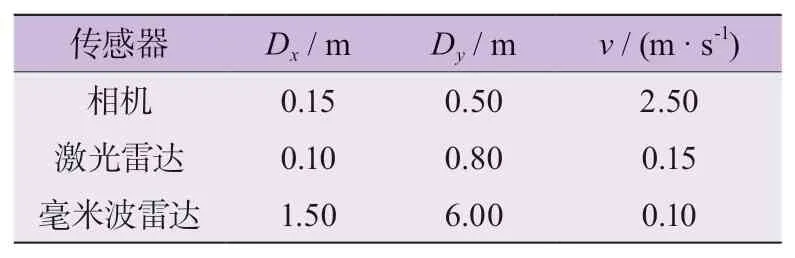
表1 大地坐标下各传感器精度

各传感器通过各自的检测算法获取目标车辆的状态信息：位置、速度、加速度、角速度等。各传感器的部署情况如图3所示。相机、毫米波雷达覆盖范围近似为梯形，激光雷达覆盖范围近似为圆环形，覆盖整个丁字路口。3个传感器架设高度为12.4 m。本实验采用一辆装有差分高精度GPS（global positioning system，全球定位系统）的实验车辆，在3个传感器的覆盖范围内行驶，车载GPS用以获取实验车辆位置及速度的参考值。

图4 —图6所示为横向距离Dx、纵向距离Dy、合速度v这3个参数的不同传感器感知结果、传统EKF算法融合结果以及本文AEKF算法融合结果。相机、激光雷达对目标车辆位置的识别较精准，毫米波雷达的位置识别差异性较大；毫米波雷达、激光雷达对目标车辆合速度的识别较精准，相机对合速度的识别波动性大。本文AEKF算法，相较于单传感器的测量值而言，融合后的结果精度得到了提高，此外相较于传统EKF算法；因此，本文AEKF算法能提高估计的精度，降低噪声干扰。

统计计算出各传感器测量值以及融合算法估计值相对于GPS参考值的均方根误差,对其进行定量比较。表2列出了各传感器的测量值、传统EKF算法以及所提AEKF算法针对横向距离Dx、纵向距离Dy、合速度v的均方根误差RMSE指标。

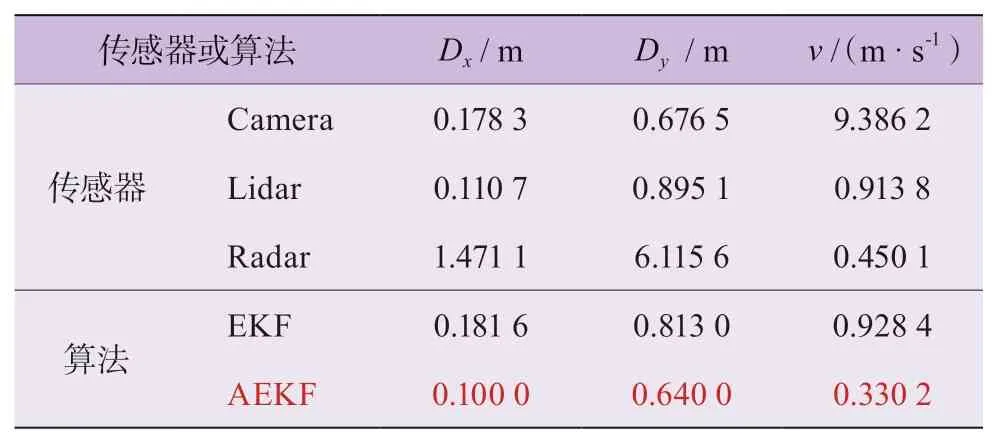
表2 传感器测量值、EKF以及AEKF算法的RMSE指标

据表2可以看出：本文的AEKF算法提高了估计精度；相较于单传感器的测量值而言，横向距离估计精度提高了9.7%，纵向距离估计精度提高了5.4%，速度估计精度提高了26.6%，相较于传统EKF而言，横向距离估计精度提高了44.9%，纵向距离提高了21.3%，速度估计精度提高了64.4%；本文方法使目标速度的估计精度明显提高。

本文AEKF算法和传统EKF算法的相关参数如表3所示（见下页），AEKF算法和传统EKF算法的相关参数初值相同。

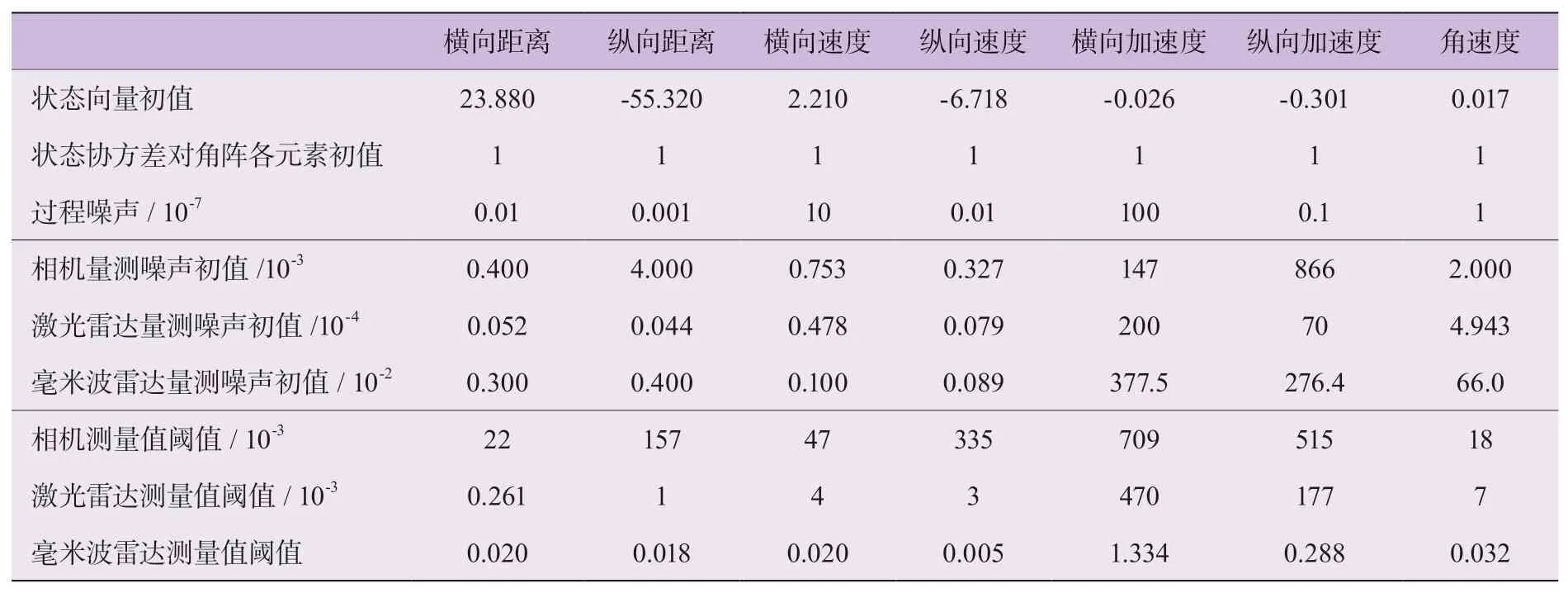
表3 AEKF算法和EKF算法相关参数

3 结 论

针对路侧多传感器融合过程中的传感器误差特性难以在线获取、且动态定量描述困难等制约，本文作者:

1） 提出了一种量测噪声在线获取方法，利用一定时间序列的不同传感器的测量值，通过多项式拟合的方式，求取测量值序列的残差，进而利用方差函数生成初始化量测噪声。

2） 提出了基于AEKF的路侧多传感器融合方法，对多源异质信息进行融合。通过对传感器测量值的稳定性进行检测，利用修正系数自适应的调整量测噪声矩阵，降低了量测噪声对系统估计的影响。实车试验结果表明：相较于单传感器的测量值而言，基于量测噪声自适应调整融合后横向距离估计精度提高了9.7%，纵向距离估计精度提高了5.4%，速度估计精度提高了26.6%。对比于传统的EKF算法，本文AEKF算法提高了估计精度，降低了噪声干扰。

本文研究仅考虑量测噪声对系统估计的影响，由于动态系统噪声是由过程噪声和量测噪声共同组成，同时考虑过程噪声和量测噪声影响条件下，路侧多传感器对交通目标的融合感知方法有待进一步研究。