直达声场试验平台的数值仿真方法研究

荣吉利， 张博涵， 程修妍， 范博超， 秦朝红， 李海波， 魏龙

(1. 北京理工大学 宇航学院，北京 100081；2. 北京强度环境研究所，北京 100076)

航天器在发射和飞行过程中，环境气动噪声[1]以及发动机喷流噪声[2]等极易导致航天器内有效载荷被破坏. 为考核航天器承受噪声环境的能力，有必要在地面真实复现发射过程的噪声环境. 噪声试验是航天器地面试验的一种关键试验技术，用于检验航天器在噪声环境中的抗噪性能[3].

目前针对航天器结构，常用的噪声试验方法主要有混响场试验和行波场试验[4]. 混响场试验应用最为广泛，能模拟航天器所经受的噪声环境从而检验其可靠性. 大型航天器的噪声试验一般在混响室进行，使用气源在混响室内产生需要的声谱以模拟航天器在整流罩内所经受的噪声环境[5]. 但每开展一次试验需要消耗大量气源，且对试验场地也有严格要求[6]，而直达声场试验技术(DFAT)只需将试验件置于扬声器围成的阵列内部，通过扬声器直接对试验件产生噪声激励来模拟航天器外的噪声环境. LARKIN等[7]讨论了直达声场试验优势，与混响试验相比，直达声场试验具有空间自由、成本低、周期短等优点；鲍尔航空航天技术公司利用扬声器阵列代替混响室对航天器开展了噪声试验，节省了时间和物力成本[8]；Sandia 国家实验室[9]用商用扬声器搭建了小型 DFAT 试验系统，节省了试验空间；KOLAINI等[10]研究了影响直达声场试验可靠性的因素，发现试验件结构模态和驻波的耦合作用可能会导致过试验；Maryland Sound International(MSI)使用多输入-多输出(MIMO)控制策略控制扬声器阵列，有效降低试验声场的相关性，使声场与实际飞行声场更接近[11]. 混响声场试验主要针对的试验对象为整流罩、飞行器等系统级试验，而直达声场试验适合仪器、组件等设备级试验，两者分工有所区别，因而需要根据实际情况具体分析需要采取哪一种试验手段.

直达声场试验结果受很多因素影响，因而需要通过仿真预示选取合理的试验区域开展试验. MSI联合ESI软件公司对DFAT进行了仿真分析[12]；Sandia国家实验室在试验基础上利用有限元方法开展了相关仿真工作[13]；ROUSE等[14]采用平面波表征扬声器对直达声场进行了模拟分析；洛克希德·马丁公司利用边界元方法对直达声场展开了仿真分析，采用单极子声源替代扬声器，对DFAT的开展起到了预示作用. 但无论是平面波或是单极子，声源都太过理想化，且不够直观，不能很好表征扬声器的声学特性. 本文利用速度边界代替完整扬声器建模，仿真验证该等效方法的可行性；基于此方法建立直达声场有限元模型，提升计算效率，并比较直达声场与混响声场的响应结果，对直达声场试验的试验平台搭建提出参考建议.

1 混响声场声源模型

1.1 平面波叠加法

混响室试验是航天器噪声试验的主要技术手段，为验证直达声场仿真模型可靠性，首先需要建立混响声场模型作为比较对象. 混响声场是一种声场内各位置声能量向各个方向的传播概率相同、平均声能密度均匀的弥散场，使用平面波叠加的方法是仿真中模拟混响声场的常用方法.

设某瞬时到达声场某位置的两列声波为

(1)

(2)

1.2 混响声场声源模型建立

使用LMS Virtual.lab软件建立圆柱声腔网格，半径850 mm、高1 700 mm；属性定义为空气，其外表面设置为无反射边界面，使得声波能无反射的自由透过外表面，底面定义为反射面模拟地面反射作用；使用分布式平面波作为声源产生混响激励[16]，采用混响试验常用声压级频谱作为输入，如表1所示.

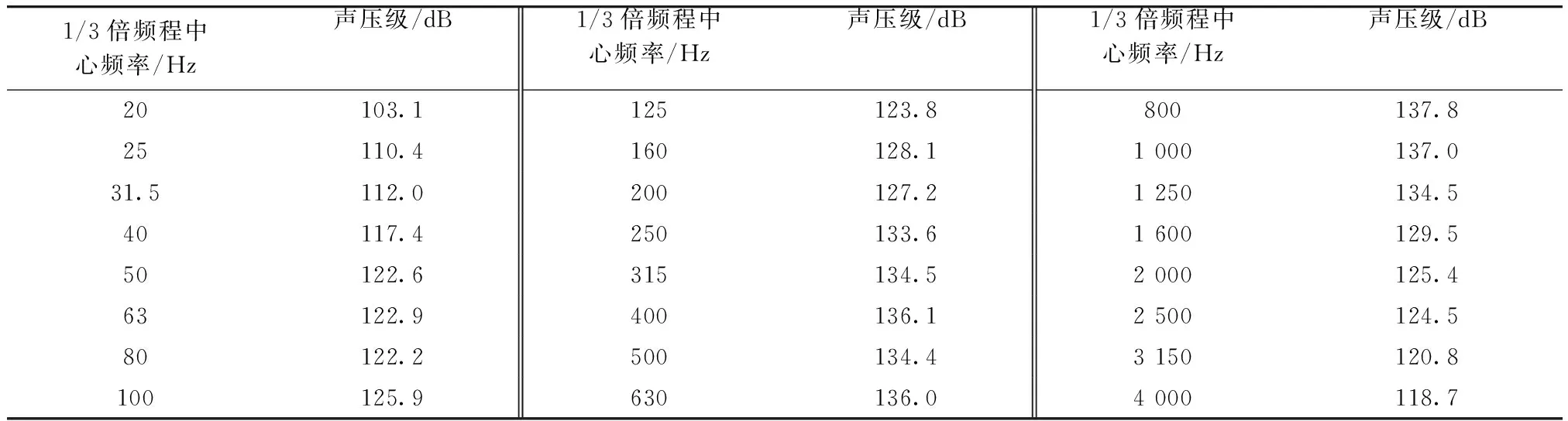
表1 平面波的输入声压级Tab.1 Input SPL of plane waves

混响声场模型如图1所示，计算频率范围20～4 000 Hz. 在声腔内随机取5个测点绘制声压级响应曲线，如图2所示. 可以看出各随机测点声压级响应基本一致，表明声场均匀性良好；声场内声压级响应与输入声压级接近，与理论相符，可用于表征混响声场.

图1 混响声场模型Fig.1 Reverberation field model

图2 混响声场声压级响应曲线Fig.2 SPL response curves of reverberation field

2 扬声器声源等效方法

直达声场试验声源为扬声器阵列，在数值计算时如果直接建立扬声器模型并基于声振耦合计算求解响应需要花费大量时间，还需要考虑扬声器振膜材料、连接方式等问题. 本节提出了一种利用速度边界等效扬声器的仿真方法，仅需测得扬声器振膜附近声压并将之赋值到对应面上即能产生和扬声器相近的激励效果，提高了直达声场数值仿真效率.

2.1 速度边界方法

设想在无限均匀介质中存在一列沿着x方向传播的平面声波，已知其振幅为pa，可利用波动方程解得声场中声压为：

p(t,x)=paej(ω t-k x)

(3)

(4)

通过上式能够将声压以速度边界条件的形式赋值到任意选定的面上，使该面作为声源产生激励. 以扬声器为例，先测得扬声器振膜附近声压，将之赋值到对应的速度边界面上作为声源，就可以省去完整的扬声器建模及声振耦合计算过程，提升计算效率.

2.2 速度边界等效扬声器可靠性分析

2.2.1指向性对比

扬声器的指向性是由扬声器原理、结构、本身特性决定的，是扬声器的重要指标. 为验证速度边界等效扬声器方法的可靠性，本节建立了一个通用扬声器模型，得到其指向性图以及振膜位置处声压，再将振膜处声压通过速度边界条件定义到新的模型振膜面上，得到等效模型的指向性图，对比两种情况下指向性差异.

采用通用的扬声器模型[13]，利用边界元方法，定义介质为空气，导入振膜模态和激振力，计算频率为50～1 000 Hz. 在扬声器振膜表面外布置面场点，如图3所示，测得振膜位置声压，根据式(4)通过速度边界等效的方式定义到扬声器振膜面位置，以此为声源计算等效模型指向性，计算频率为50～1 000 Hz. 指向性圆位置定义为以两振膜之间中心位置为参考点、半径为1 000 mm的半圆周上，如图4所示.

图3 扬声器模型Fig.3 Loudspeaker model

图4 指向性圆位置Fig.4 Position of the directional circle

通过仿真比较6个频率下两种情况的指向性如图5所示，纵坐标为归一化指向性因子，即声压幅值与圆周上声压最大值的比值，表征声场幅度随方向而变化的趋势.

图5 不同频率下扬声器与等效模型指向性对比Fig.5 Directivity comparison between loudspeaker and equivalent model at different frequencies

通过图5可知，等效模型指向性与实际扬声器基本一致，在300，600 Hz由于等效模型速度边界面为平面，而实际的扬声器振膜面是曲面，导致了指向性在小角度范围内存在差异. 在实际的直达声场试验中，小角度范围(0～30°、150～180°)产生的声波对试验件放置位置的影响较小，所以该指向性差异可忽略.

2.2.2声压级对比

在扬声器振膜一侧正中心前方依次布置4个测点，距离振膜面分别为300、600、900、1 200 mm，如图6所示. 计算两种情况下振膜面外不同距离处的声压级响应，如图7所示，峰值以及总声压级如表2所示. 总声压级可由式(5)计算得到.

图6 测点分布Fig.6 Distribution of measurement points

(5)

由图7以及表2可知，两种情况声压级响应趋势接近，峰值误差在2 dB以内，总声压级误差在 3 dB以内，这表明速度边界等效方法建立的仿真模型响应结果与扬声器接近，验证了该方法可靠性.

图7 不同距离处扬声器与等效模型声压级响应对比Fig.7 Comparison of SPL responses between loudspeaker and equivalent model at different distances

表2 峰值及总声压级对比Tab.2 Comparison of peak SPL and OASPL

3 直达声场仿真模型

本文以每列排列4个、共5列，总数20个扬声器为例，建立小型直达声场仿真模型，选择5列扬声器是是因为对称性强的阵列构型易导致驻波影响变大，声场均匀性下降[7]，所以选取了奇数扬声器阵列. 采用第2节提出的速度边界等效方法取代扬声器完整建模，仅需建立扬声器阵列中的空气声腔有限元网格，在网格外表面按照扬声器的空间排布定义出相应的速度边界面用以取代扬声器产生激励，利用反射边界表征扬声器箱体，并设置底面为反射面模拟地面的反射作用. 为更符合实际，扬声器之间的间隙则定义为无反射边界，使得声波能够从这些空隙中散射出去. 直达声场有限元模型建立流程如图8所示.

图8 直达声场模型建立Fig.8 Direct field model establishment

(6)

受地面、扬声器箱体反射等因素影响，直达声场内并非处处均匀. 为更接近混响声场，需要筛选声压分布相对均匀的区域. 仍根据表1定义输入声压pTotal，依据式(6)定义速度边界面作为激励后进行仿真计算，分别在以声腔中心为体心，边长为200，400，600，800 mm的立方体每个面中心取测点，每个区域6个测点，如图9所示. 计算得到声压级响应曲线如图10所示. 对比发现随着测点远离直达声场中心区域，测点间声压级响应差异变大，说明声场均匀性由直达声场中心往外侧逐渐减弱.

图9 声场内测点位置Fig.9 Position of measuring points in direct field

图10 直达声场内不同区域声压级曲线Fig.10 SPL curves of different regions in direct field

将直达声场中均匀性较好的200 mm立方体区域6个测点取声压平均值，与混响场内多个测点平均值进行对比，绘制声压级响应曲线如图11所示，两种情况峰值、总声压级以及差值如表3所示，对比发现直达声场与混响声场声压级趋势接近，峰值声压级以及总声压级差值均在3 dB以内，说明在该区域内直达声场能达到与混响场接近的响应效果，在直达声场试验中可选取该区域对试验件进行噪声测试.

图11 直达声场与混响声场声压级曲线Fig.11 SPL curves of direct field and reverberation field

表3 峰值及总声压级对比Tab.3 Comparison of peak SPL and OASPL

4 结 论

本文通过定义速度边界等效扬声器激励的方法建立了一种直达声场试验平台的仿真模型，与混响声场结果对比验证了该模型的可行性. 所得结论如下：

① 使用平面波叠加法作为声源建立了混响声场声源模型，仿真验证了声场均匀性符合混响场要求，可作为直达声场参照.

② 提出了定义速度边界作为激励简化扬声器模型的方法并与真实的扬声器模型进行对比，结果表明两者指向性吻合良好，各测点声压级响应趋势接近，峰值声压级和总声压级误差在3 dB以内，验证了该方法的可行性.

③ 基于速度边界等效方法建立的直达声场模型，声场内声压均匀性由内向外呈减弱趋势，在声场中心边长200 mm立方区域内均匀性最好，该区域内测点平均值与混响声场相比，峰值声压级和总声压级差值都在3 dB以内，验证了该模型有效性，能为直达声场试验平台搭建提供参考.