土岩复合地层隧道盾构开挖地表沉降Peck公式修正

刘俊杰，刘俊伟，2，任晓敏，贾宁

（1.青岛理工大学 土木工程学院，山东 青岛 266033；2.山东半岛蓝色经济区工程建设与安全协同创新中心，山东 青岛 266033；3.中建八局轨道交通建设有限公司，江苏 南京 210046）

0 引言

如今越来越多的城市都在修建地铁，盾构隧道以其安全性、高效性、实用性等优势被广泛采用。然而地下隧道的开挖会打破原有土体的应力平衡状态，同时由于施工中水土流失、土层固结和施工方法不当等会造成城市地表沉降，地表沉降过大不仅对周边建筑、地下管线造成一定影响，而且严重时会引起地表塌陷，影响隧道施工和周边环境安全。针对此类工程问题已经有许多研究成果，研究方法主要有经验公式法、数值模拟法、模型实验法、理论解析法等。

经验公式法以简便易用的特点被大量研究采用，Peck公式经验法［1］是所有经验公式法中最简便、应用最多的方法，自1969年被提出后在世界各国获得广泛使用，但是由于各地区工程条件和技术手段等不同，Peck公式预测值与各地区实测数据具有一定差距，因此，很多学者根据不同地区的隧道开挖情况对Peck公式进行了适用性修正。胡长明等［2］基于西安富水砂层地铁区间隧道施工引起的地表沉降数据对Peck公式进行修正；路林海等［3］结合Peck公式建立了黏性土地层中小半径曲线隧道盾构施工过程中地表沉降量预测公式；田晓艳等［4］基于叠加理论的经验法预测双线隧道开挖的地表沉降量，并利用FLAC 3D进行了模拟验证；陈春来等［5］基于Peck公式建立双线平行盾构隧道施工中三维土体沉降量的计算方法。

数值模拟应用中，G.W.Clough［6］通过二维平面应变数值模型分析了盾构隧道掘进过程中土体的应力和变形规律；刘红兵［7］运用三维有限差分法对盾构隧道施工引起地表沉降进行全面分析，得到地层变形的三维特征；冯慧君等［8］基于FLAC 3D软件模拟了双线盾构隧道开挖过程，验证双线盾构隧道施工导致地表沉降的叠加效果。

关于隧道开挖的室内模型试验研究较多。刘泉声等［9］采用地质力学模型试验方法全方面研究了特大断面浅埋暗挖隧道周边土层的应力与位移变化情况；YANG S Q等［10］通过三轴大型模型试验系统研究了深埋复合地层中TBM开挖地层的位移变形特征；FANG Y等［11］通过1g模型试验建立了一个基于高斯曲线的方程预测隧道开挖引起的纵向地表沉降量。

理论解析方面，姜忻良等［12］提出了计算不同深度土层沉降槽曲线宽度系数的公式，为计算隧道开挖引起地表以下任一点竖向沉降提供了有效的计算方法；卢海林等［13］根据地层损失的空间分布规律，应用镜像法原理计算得到隧道周围土体的位移和应力分布；谷拴成等［14］运用随机介质理论对隧道开挖过程中地表沉降量进行了预测计算。

上述研究背景集中于软土地层，对于土岩复合地层的相关研究较少，土岩复合地层浅层为软土或软岩，深层为较硬的岩层，整体表现为上软下硬，各层岩土体性质差异性较大。青岛属于此类工程地质条件，地层为上土下岩，竖向分布不均匀，隧道开挖面存在软层、硬层、软硬复合地层等多种情况，这使得青岛地区的隧道开挖与其他地区存在明显差异，施工难度更大，对于此类特殊的工程问题需要一定的理论与技术经验指导。本文采用回归分析对Peck公式进行线性拟合，并结合青岛市地铁8号线某区间隧道盾构掘进时的地表沉降量监测数据对Peck公式做出适用性修正，对比分析计算值与实测值，验证了计算模型的可行性和准确性，研究结果可为青岛地铁隧道的开挖和类似土岩复合地层的盾构隧道施工提供参考与帮助。

1 工程概况及沉降监测

1.1 工程概况

青岛市地铁8号线隧道区间地形较为平坦，地面高程1.9～5.8 m，地下水为孔隙承压水和基岩裂隙水，水位埋深较高。隧道采用土压平衡盾构机施工，隧道内径5.4 m，外径6 m，隧道顶覆土深度约12 m，隧道开挖断面多为土岩复合地层。根据场地勘察情况，该工程场地土层物理力学参数如表1所示，自上而下地质横剖面图如图1所示。

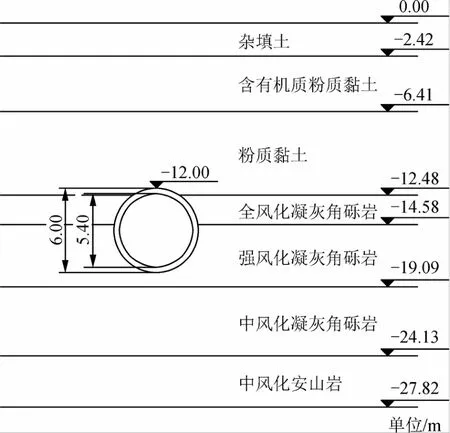
图1 土层地质横剖面Fig.1 Soil geological profile

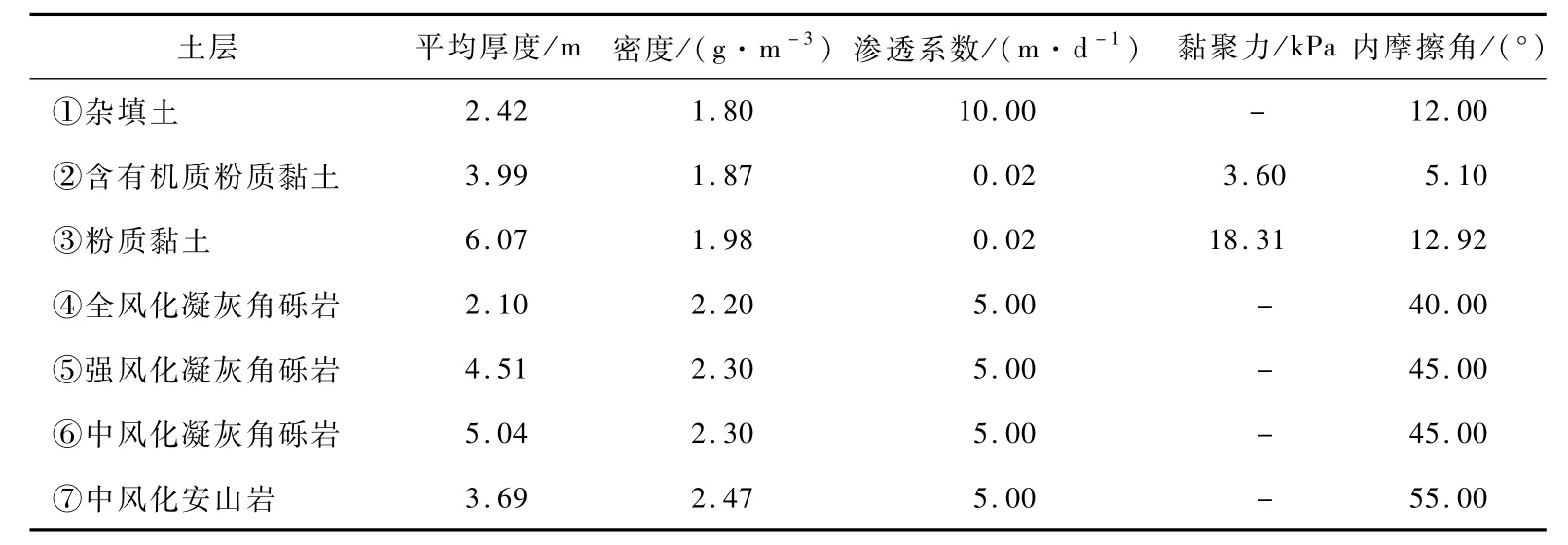
表1 土层物理力学参数Tab.1 Physical and mechanical parameters of soil layers

1.2 地表沉降监测

隧道盾构开挖对地表沉降影响非常大，在采取一定控制措施的同时进行地表沉降监测必不可少。在该地铁线路上全线布置监测点，主要横断面平均布置7个监测点，间距为5 m，各个主断面间距平均为30 m，主断面测点布置如图2所示。采用钻孔中埋入钢筋的方式布置监测点，如图3所示，监测仪器为天宝电子水准仪和配套的铟钢尺，采用几何水准测量方法测量。

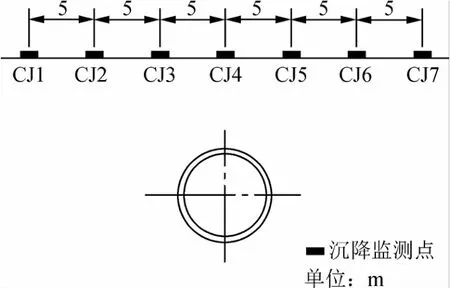
图2 地表沉降监测点布置示意Fig.2 Layout of monitoring points for surface subsidence

图3 沉降监测点Fig.3 Surface subsidence monitoring point

2 Peck公式与线性回归

1969年，Peck结合大量工程实践沉降监测数据和相关工程资料分析认为，隧道盾构施工产生的地表沉降横向分布近似为正态分布曲线。不考虑土体排水固结和蠕变，假定地层损失在整个隧道长度上均匀分布的情况下，隧道开挖形成的地表沉降槽体积应等于地层损失的体积［15］，并在国际土力学大会上系统地提出了地表横向沉降的计算方法，即Peck公式［16］，见式（1），地表横向沉降槽曲线如图4所示。

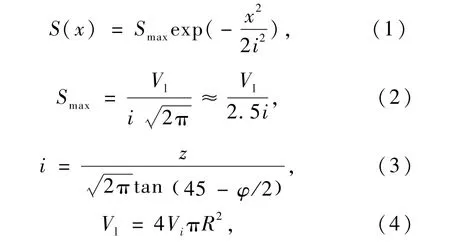
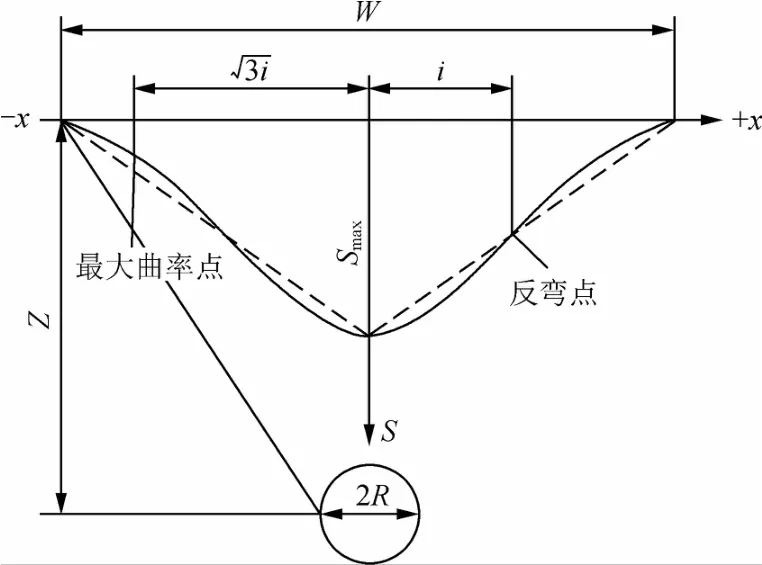
图4 地表横向沉降槽Fig.4 Surface transverse settling tank

式中：S（x）为距隧道中轴x处地表沉降量；Smax为隧道正上方的地表沉降值；i为地表沉降槽宽度；Vl为施工引起的隧道单位长度地层损失量，即隧φ为土体内摩擦角；道施工中实际开挖土体的体积与竣工隧道的体积之差；z为隧道中心轴线处埋深；Vi为地层体积损失率，即单位长度地层损失占单位长度盾构体积的百分比；R为盾构机半径。

选取青岛市地铁8号线隧道4个不同横断面地表沉降监测数据绘制曲线，如图5所示，可以看出，地表沉降量与距离隧道中心轴线距离的关系近似呈正态分布，这与Peck理论十分吻合，两变量之间存在一一对应的关系。

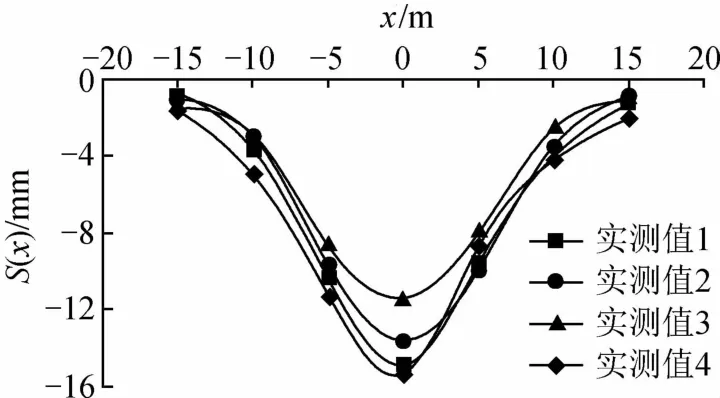
图5 实测地表沉降曲线Fig.5 Measured surface subsidence curves

采用线性回归分析拟合Peck公式中相关关系，对Peck公式两边取对数得到

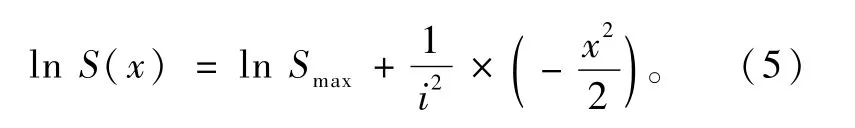
以lnS（x）和-x2/2为回归变量进行求解，令lnSmax为回归后的常数项，1/i2为回归后线性系数，为简化记号，令

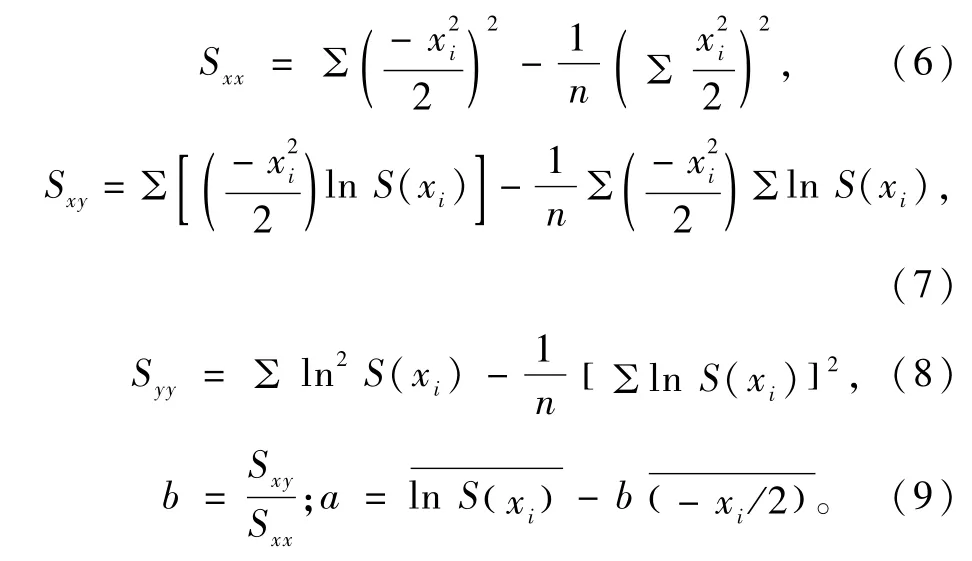
回归后转变为

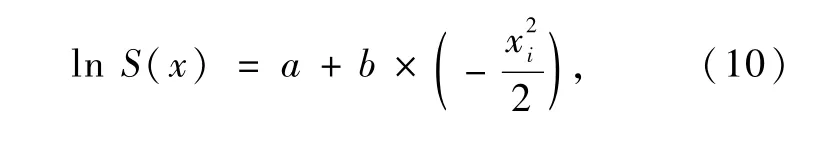
式中：a为回归方程中的常数项；b为回归方程中的线性系数；xi为第i个沉降监测点到隧道中线的距离；n为样本点个数。

由此得到线性回归后Smax值及地表沉降槽宽度i，即：

3 实测地表沉降值回归分析

随机选取青岛市地铁8号线隧道4个断面的地表沉降监测数据进行回归分析。各断面沉降监测数据见表2～5，将表中计算得到的结果代入式（6）～（9）中计算线性回归参数，结果见表6。

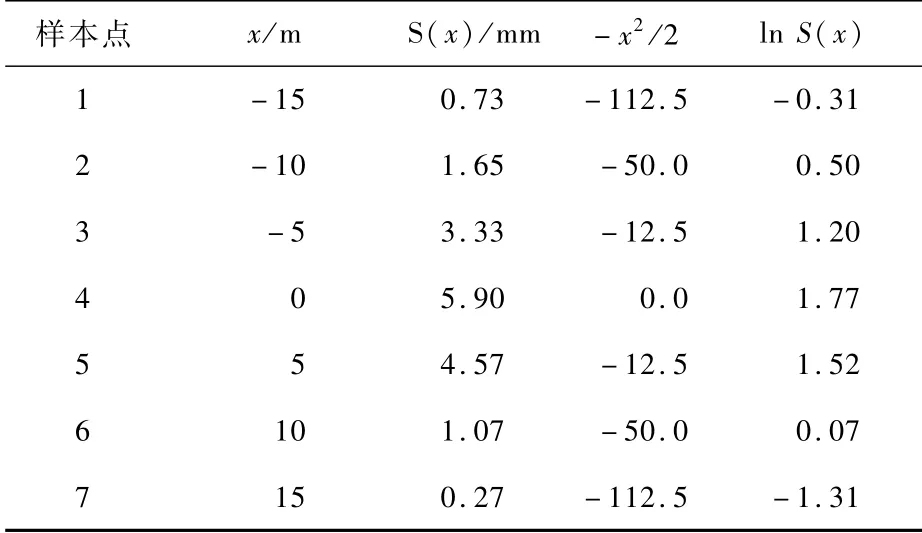
表2 断面1地表沉降数据Tab.2 Surface subsidence data of section 1

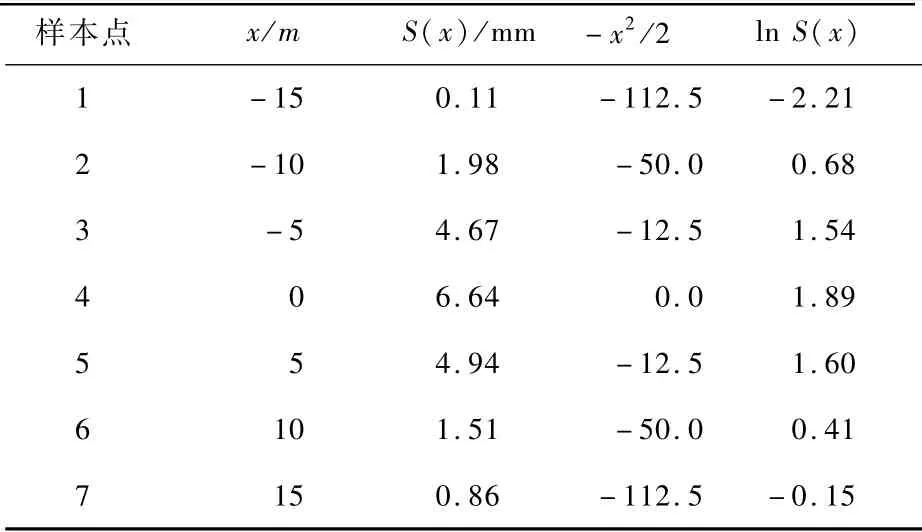
表3 断面2地表沉降数据Tab.3 Surface subsidence data of section 2

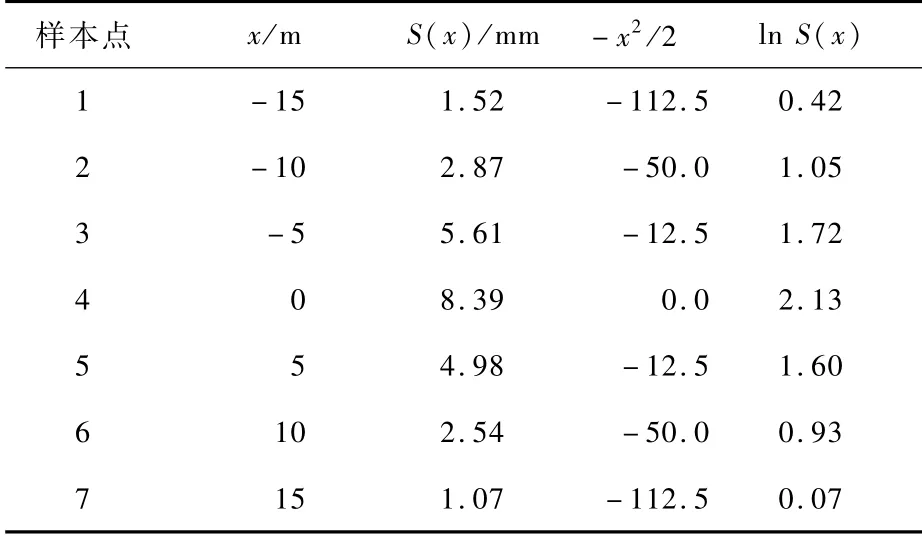
表4 断面3地表沉降数据Tab.4 Surface subsidence data of section 3

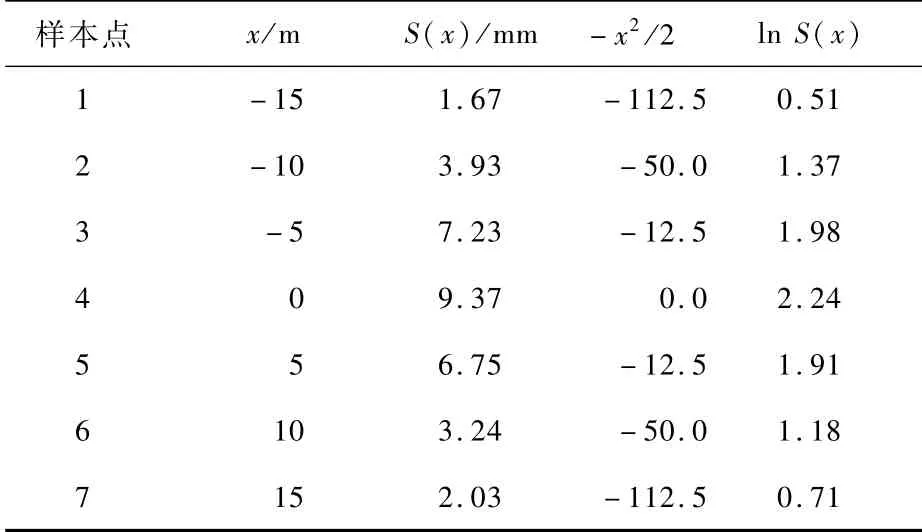
表5 断面4地表沉降数据Tab.5 Surface subsidence data of section 4

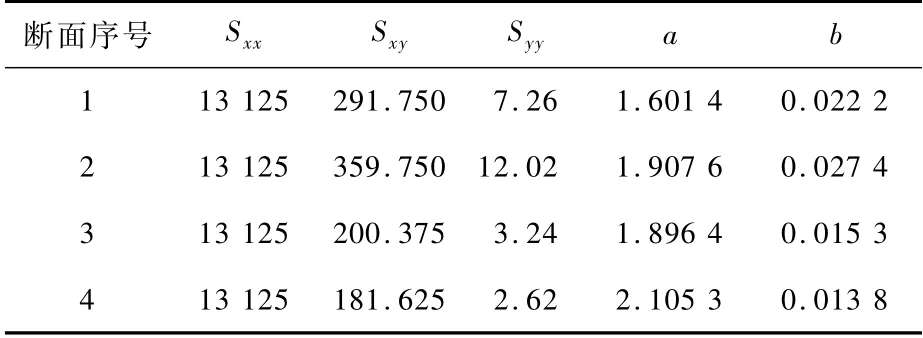
表6 各断面回归参数Tab.6 Regression parameters of each section

由表6中4个断面回归参数和式（10）得到各断面回归后的线性函数

采用数理统计中的r检验法测定拟合程度，即变量lnS（x）的各个监测值点聚在回归曲线周围的紧密程度，通常用线性相关系数r表示，

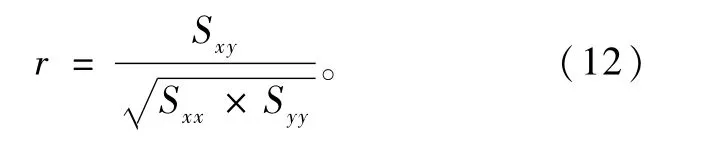
当r＞r0.01（n-2）时，可以判断回归函数线性关系高度显著，其中n为每个断面的监测点数量。计算各断面相关系数分别为r1=0.945，r2=0.905，r3=0.971，r4=0.960，r0.01（5）=0.875，4个断面的相关系数r均大于r0.01（5），线性关系高度显著。绘制回归函数图，与实测数据对比，如图6所示，可以看出运用线性回归拟合分析的方法效果较好，能够很好地表示公式转换后实测数据的相互关系。

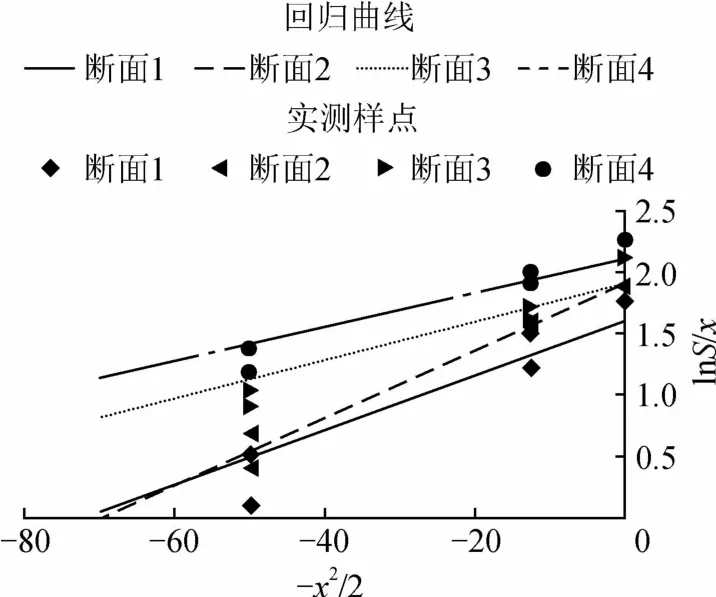
图6 各断面回归函数Fig.6 Regression function of each section

根据计算得到的a、b值由式（11）可以计算出回归后的Smax和i，代入式（1）得到回归分析后的Peck公式。

对比分析各断面的回归Peck公式曲线、实测数据曲线和原始Peck公式曲线，如图7所示。其中原始Peck公式确定需要地层损失量Vl和地表沉降槽宽度系数i两个参数。根据土层参数和地区施工经验，取φ=42°，Vi=0.01［17］，由式（2）～（4）计算可得i=13，Smax=22 mm，Vl=0.7 m3/m。即该地区原始Peck公式为

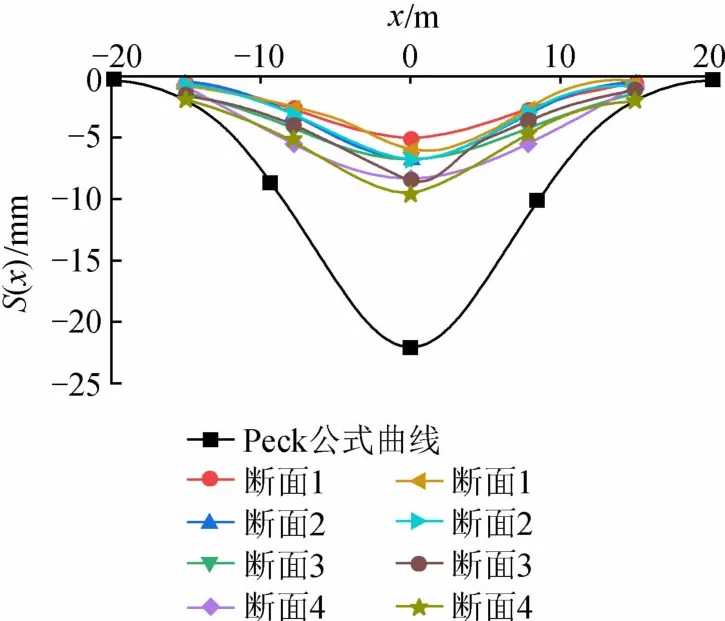
图7 各断面拟合、实测和Peck公式曲线对比Fig.7 Comparison of fitting，measured curves and Peck formula curves for each section

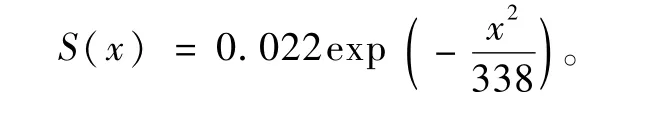
由图6可以看出，采用线性回归拟合的回归Peck公式曲线与实际测量值非常吻合，证明线可用于预测青岛市地铁8号线隧道盾构施工引起的地表沉降。与原始Peck公式相比，该方法在地表沉降预测上的准确度提升明显。

4 Peck公式修正

由于原始Peck公式不能很好地满足实际工程要求，需要对其进行修正以满足精度需求。由图8可以看出，回归Peck公式曲线与原始Peck公式曲线形态上偏度一致、峰度不同，可以分别增加地表最大沉降修正系数α、沉降槽宽度修正系数β对原始Peck公式中的两个关键参数Smax和i进行修正，见式（13）。影响地表沉降的因素非常多，如工程环境、施工方法、人员操作程序等，此处修正系数只考虑综合影响结果。

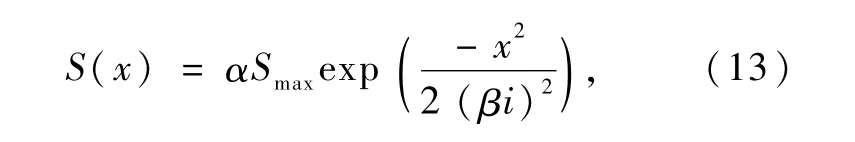
线性转换后得

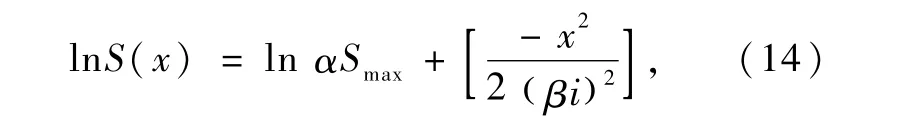
根据式（11）得

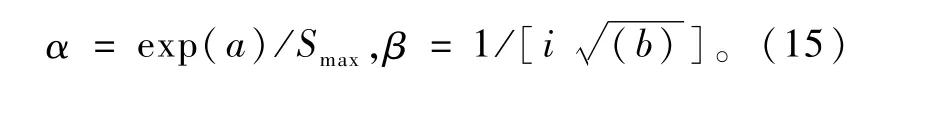
计算4个断面的修正系数分别为α1=0.23，β1=1.00；α2=0.31，β2=0.90；α3=0.30，β3=1.21；α4=0.37，β4=1.27。仅分析4个断面数据并不能反映出青岛土岩复合地层盾构隧道掘进过程中地表沉降的相关规律，因此根据工程资料对青岛市地铁8号线随机50个断面的修正系数统计归纳，其α，β值分布如图8～9所示。

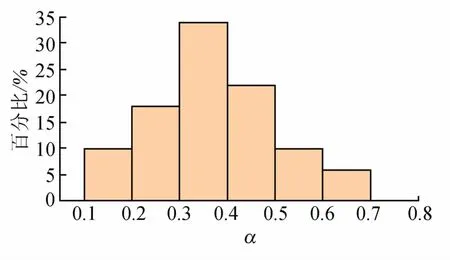
图8 地表最大沉降修正系数α分布Fig.8 Distribution of correction coefficientαfor maximum surface subsidence

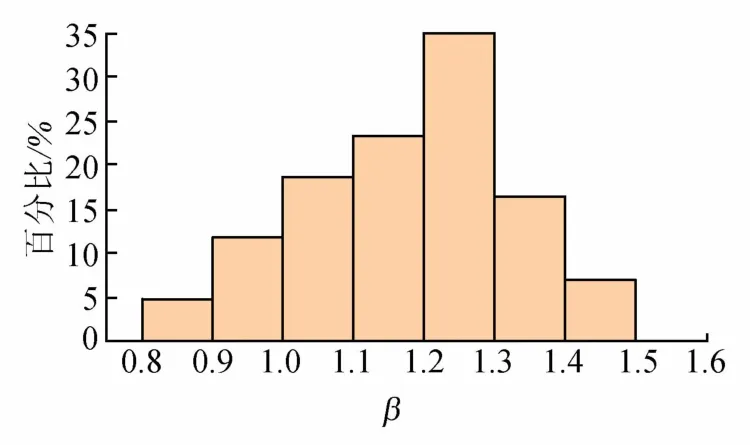
图9 沉降槽宽度修正系数β分布Fig.9 Distribution of correction coefficientβ for settlement tank width

由图8～9可以看出，α主要分布在（0.2，0.5），占全部分布区间的74%，β主要分布在（1.0，1.4），占全部分布区间的80%。这些区间的α，β可以较好地修正Peck公式，使其更好地拟合和预测青岛土岩复合地层盾构隧道掘进时地表沉降量。同时归纳计算得到的a和b，其对应分布如图10～11所示，a主要分布在（1.6，2.8），占全部分布区间的90%，b主要分布在（0.010，0.022），占全部分布区间的84%。

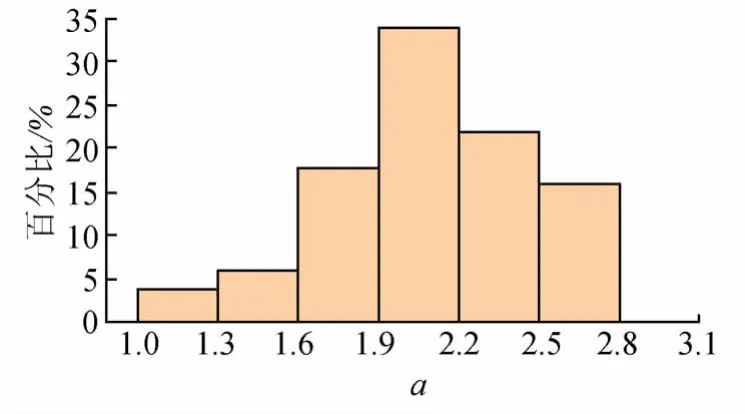
图10 回归常数项a分布Fig.10 Distribution of regression constant term a

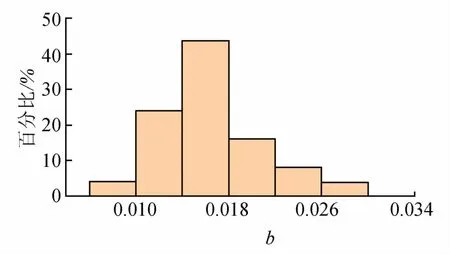
图11 回归线性系数b分布Fig.11 Distribution of regression linear coefficient b

5 结论

（1）青岛土岩复合地层盾构隧道掘进时地表横向沉降曲线同Peck公式曲线形态一致，为正态分布曲线，但Peck公式曲线与实际数据曲线差异性较大，需要修正后才能适用于实际工程。

（2）通过对Peck公式回归分析得到的拟合曲线与实测值吻合度高，引入地表最大沉降修正系数α、沉降槽宽度修正系数β对经验Peck公式进行修正。结果表明，修正后曲线可以比较精准地预测青岛土岩复合地层盾构隧道掘进地表沉降量。由50组实测数据统计，α和β分别在（0.2，0.5），（1.0，1.4）得到的修正Peck公式精度最高，对应a、b所在区间分别为（1.6，2.8），（0.010，0.022）。

（3）Peck公式受地区工程背景影响因素较大，本文结论具有一定局限性，仅适用于相似地区理想预测模型的建立及相关分析，其他地区的公式修正需要结合实际数据和当地经验参数进行分析。