Updating Mass and Stiffness Matrices Using Eigenstructure Assignment Methods

(1.School of Mathematics and Statistics,Hubei Normal University,Huangshi 435002,China;2.Library of Hubei Normal University,Huangshi 435002,China)

Abstract:A novel numerical method is presented to update mass and stiffness matrices simultaneously with measured vibration data by means of the combined acceleration and displacement output feedback.By the method,the required displacement and acceleration output feedback gain matrices are determined,and thus the optimal approximation mass matrix and stiffness matrix which satisfy the required orthogonality relation and eigenvalue equation are found.The proposed method is computationally efficient and the updated mass and stiffness matrices are also symmetric and have the compact expressions.The numerical example shows that the proposed method is reliable and attractive.

Keywords:Model updating;Undamped vibration system;Eigenstructure assignment;Acceleration and displacement feedback;Optimal approximation

§1.Introduction

By the finite element technique,vibrating phenomenon of a mechanical structure with feedback control can be modelled by

whereMa,Ka ∈Rn×nare the analytical mass and stiffness matrices,respectively.In general,Mais symmetric and positive definite,andKais symmetric and positive semi-definite.Equation(1.1) is usually known as the finite element model (FEM).q(t)∈Rn×1is the position vector,B ∈Rn×mis the full column rank control feedback matrix andu(t)∈Rm×1is the control vector.In addition,the output or measurement vectory(t)∈Rr×1is given by

whereCis a realr×noutput matrix,and is generally assumed to be full row rank.For the static output feedback,u(t) could take the following particular form:

whereGdandGa ∈Rm×rare displacement and acceleration output feedback gain matrices,respectively.Substituting (1.2) and (1.3) into (1.1) yields the following closed-loop system

Ifq(t)=xeiωtis a fundamental solution of (1.4),then the natural frequencyωand the mode shape vectorxmust satisfy the following generalized eigenvalue equation

whereis thejth eigenvalue andxjis thejth eigenvector.It has been shown that eigenstructure assignment methods are very efficient for active vibration cancellation in structures,since the eigenvalues and the corresponding eigenvectors can be assigned simultaneously [1,4,6-8,10,12].The aim of this paper is to modify the mass and the stiffness matrices simultaneously by using the acceleration and displacement output feedback so that the modified second-order system (1.4) will contain the measured eigenvalues and eigenvectors.

Specifically,the problem of updating mass and stiffness matrices simultaneously using acceleration and displacement output feedback can be stated as follows.

Problem 1.LetX ∈Rn×pbe the measured modal matrix,Λ∈Rp×pbe the measured natural frequency diagonal matrix,B ∈Rn×mbe a full column rank matrix andC ∈Rr×nbe a full row rank matrix.FindGa,Gd ∈Rm×rsuch that

whereM=Ma+BGaCandK=Ka+BGdCrepresent the corrected mass and stiffness matrices,respectively.

In order to obtain the optimal approximation matrices,we should further solve the following problem.Problem 2.LetSEbe the solution set of Problem 1.Findsuch that

where‖·‖denotes the Frobenius norm of a matrix,that is,Once the solutionof Problem 2 is obtained,then the updated mass and stiffness matrices expressed as

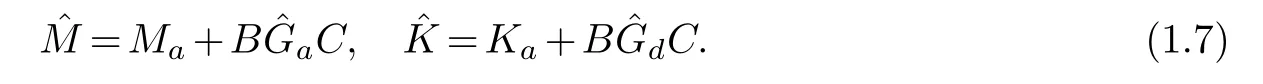
With the help of the eigenstructure assignment technique to solve the model updating problem has been considered by Minas and Inman [9] and Zimmerman and Widengren [17].The method can produce an adjusted FEM on damping and stiffness matrices with symmetric low-rank updating that matches the experimental modal data.Recently,Ouyang and Zhang [11] presented passive structural modifications of mass-spring systems for partial assignment of natural frequencies without frequency“spill-over”.Sen and Bhattacharya[13]adopted an eigenstructure assignment to update the continuous time state space model of a linear time-invariant system.More recently,Yuan,Zhao and Liu [14] developed a direct method to update the mass and stiffness matrices simultaneously using acceleration and displacement state feedback for undamped vibration systems and the explicit expressions of the updated matrices were provided.However,in most practical situations the full states are not directly available.From a practical standpoint,a more attractive procedure would be one which is based upon feeding back only the measured variables,i.e.,static output feedback [15].

It is to be noted that mathematically there is similarity between the problems of model updating and eigenstructure assignment by feedback.However the physical scenario is different.The difficulty is that the feedback used in the second-order control system leads to a nonsymmetric system although the symmetry may not be mandatory.Nevertheless,maintaining symmetry and reproduction of the measured data are the basic requirements for model updating.

Our main contribution in this paper is to provide a new numerical method to solve the FEM updating problem using the acceleration and displacement output feedback technique and the updated model has the following properties:

•The updated model will reproduce the measured eigenvalues and eigenvectors.

•The symmetry of the original model is preserved.

•The difference between the updated FEM and the original model is minimal.

We believe that the method proposed should give considerable insight into the important model updating problem.

§2.Solvability conditions of Problem 1

In order to solve Problem 1,we need the following lemmas.

Lemma 2.1.[3,p.52,Theorem 1] If,then the matrix equationhas a solutionif and only ifIn this case,the general solution of the equationcan be expressed as,whereis an arbitrary matrix.

Lemma 2.2.[5,Theorem 2] Let,then the matrix equationhas a symmetric solutionif and only ifIn this case,the general symmetric solution of the equation is

whereis an arbitrary symmetric matrix.

Let

Assume that the QR-decompositions ofBandare

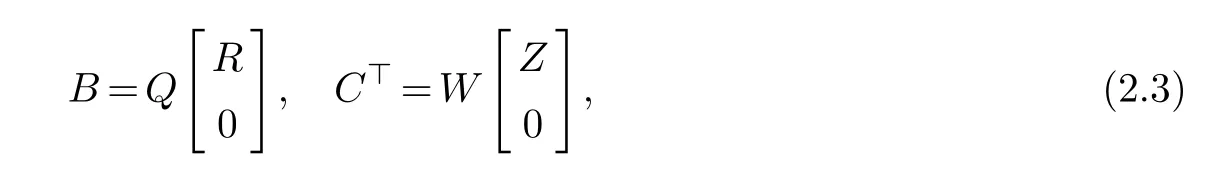
whereQ=[Q1,Q2],W=[W1,W2] aren×northogonal matrices (Q1∈Rn×m,W1∈Rn×r),andR∈Rm×m,Z ∈Rr×rare nonsingular matrices.It follows from Lemma 1 and(2.3)that Equation(2.1) with respect toGahave a solution if and only if

and the unique solution can be represented as

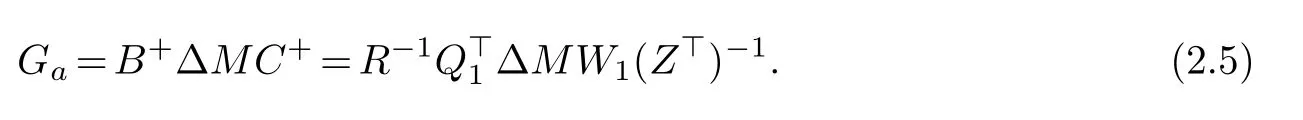
By Lemma 2,the first equation of (2.4) is always solvable with respect to symmetric matrix ΔMand the general solution is

whereSa ∈Rm×mis an arbitrary symmetric matrix.Substituting (2.6) into the second equation of (2.4),we obtain

Let the singular value decomposition ofbe

whereU=[U1,U2]∈Rm×mandV=[V1,V2]∈R(n−r)×(n−r) are orthogonal matrices,and the partitions are compatible with the size of Ω=diag{ω1,···,ωl},ωj>0,j=1,···,l,Using Lemma 2 again,the general solution to equation (2.7) with respect to symmetric matrixSa ∈Rm×mis

whereHa ∈R(m−l)×(m−l) is an arbitrary symmetric matrix.Substituting (2.9) into (2.6),we obtain the general symmetric solution of (2.4) as

whereHa ∈R(m−l)×(m−l)is an arbitrary symmetric matrix.

Similarly,by solving Equation (2.2),we can get

whereHd ∈R(m−l)×(m−l) is an arbitrary symmetric matrix.

Now,to solve Problem 1 is equivalent to finding symmetric matricesHaandHdsuch that

whereP1=Q1U2.Observe that,if letP2=[Q1U1,Q2],thenandbe an orthogonal matrix.Thus,premultiplying the first equation of (2.13)byyields

Assume that the singular value decomposition ofXis

whereL=[L1,L2]∈R(m−l)×(m−l) andF=[F1,F2]∈Rp×pare orthogonal matrices,and the partitions are compatible with the size of Σ=diag{σ1,···,σt},σi>0,i=1,···,t,t=rank.Let

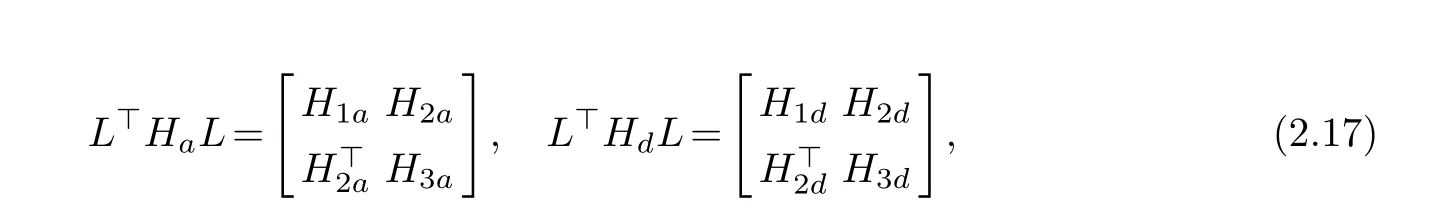
whereH1a,H3a,H1dandH3dare symmetric matrices.Substituting (2.16) and (2.17) into the second equation of (2.13) and (2.15) leads to

where,J=By substituting (2.18) into (2.20),we have

which implies thatSubstituting (2.18) into (2.21) yields

By Lemma 1,the equation of (2.23) with respect toH2ahas a solution if and only if

Thus,if the conditions

are satisfied,then we can get

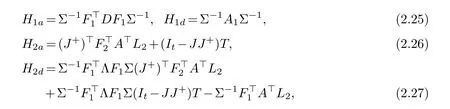
whereT ∈Rt×(m−l−t) is an arbitrary matrix.

As a summary of the above discussion,we have proved the following result.

Theorem 2.1.Assume that the QR-decompositions of B andare given by(2.3),and the singular value decomposition of the matrixis given by(2.8).Let P1=Q1U2,P2=[Q1U1,Q2]and the singular value decomposition of the matrixbe given by(2.16).WriteIf the conditions of(2.14)and(2.24)hold,then Problem1is solvable and the solution set SE of Problem1is

H2a and H2d are respectively given by(2.26)and(2.27),T ∈Rt×(m−l−t) is an arbitrary matrix,and H3a,H3d ∈R(m−l−t)×(m−l−t) are arbitrary symmetric matrices.

§3.The solution to Problem 2

In the preceding section we have shown that if the conditions (2.14) and (2.24) are satisfied,the solution setSEis nonempty.It is easy to verify thatSEis a closed convex subset of Rm×r×Rm×r.From the best approximation theorem (see Ref.[2]),we know there exists a unique solutioninSEsuch that (1.6) holds.Now,for (Ga,Gd) inSE,we can get

whereP=[P1,P2].Thus,by (2.28) we can obtain

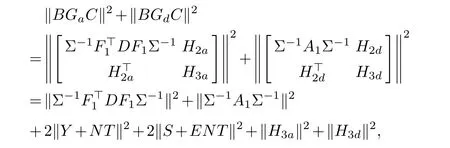
where,Therefore,‖BGaC‖2+‖BGdC‖2=min if and only if

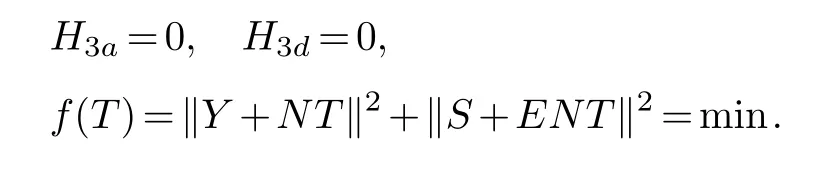
Observe that

Consequently,

Settingand noting that,we obtain

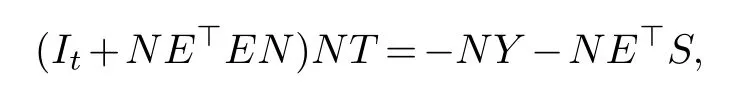
which implies that

By substituting (3.1) into (2.26) and (2.27),we get

Up to now,we have proved the following result.

Theorem 3.1.If the conditions(2.14)and(2.24)hold,then Problem2has a unique solution and the unique solution of Problem2can be expressed as

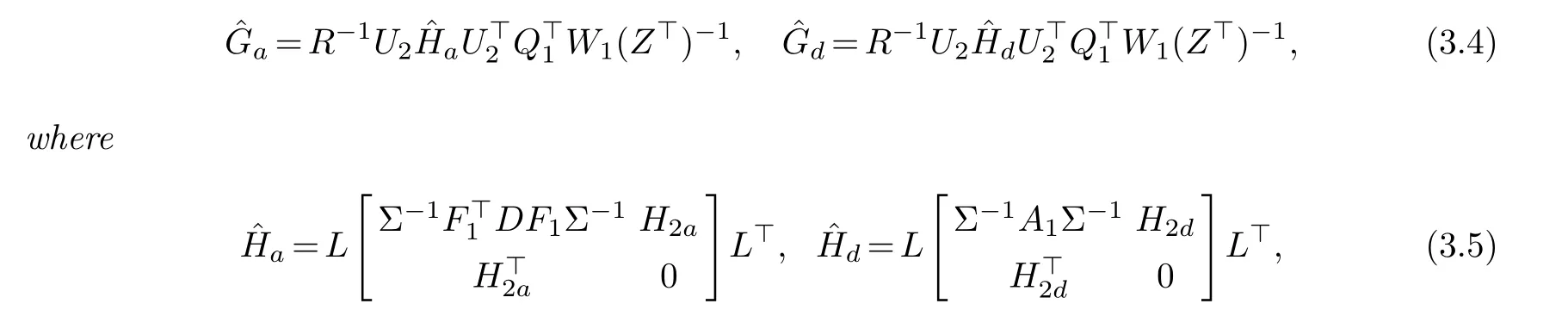
§4.A numerical example

Based on Theorem 2.1 and Theorem 3.1,we can formulate the following algorithm to solve Problem 2.

The finite element analytical matrices of the following example are taken from [16].

Example 4.1.Consider an analytical six-degree-of-freedom system with mass and stiffness matrices given by

The first three measured modal data are given by

Assume that the control feedback matrix B and the output matrix C are given by

It can easily see that the conditions(2.14)and(2.24)hold.By Algorithm 1,we obtain the unique solution of Problem2as follows.

Besides,we have

which implies that the measured modal data are implanted in the new model,and the mass normalized orthogonality constraint is also satisfied.

§5.Conclusions

A new updating method for undamped structural systems has been introduced that uses the acceleration and displacement output feedback technique to adjust mass and stiffness matrices simultaneously.The solvability conditions (Equations (2.14) and (2.24)) and the explicit expression of the unique solution of Problem 2 are presented (see,Equation (3.4)).The numerical example shows that the proposed method has the advantage of being simple and accurate which should find its applicability to a wide range of dynamic problems.