固体推进剂损伤多尺度模拟研究进展

庞维强，周 刚，王 可，李 焕

(1.西安近代化学研究所， 西安 710065； 2.陆装驻西安地区军事代表局， 西安 710065)

1 引言

随着新型含能材料的不断开发、合成及深入研究，其分子间的相互作用越来越至关重要[1]。多年来，新型含能材料的分子间相互作用研究主要以宏观实验表征为主，如DSC-TG-DTG[2]、差示扫描量热法(DSC)[3]、DSC/TG-MS[4]、高压DSC (PDSC)-TG-DTG[5-6]、量气法[7-8]、界面张力仪[9]、表面接触角法[10]、动态热机械仪[11]、扫描电镜(SEM)[12]、傅里叶红外光谱(FTIR)[13]、X-射线衍射(XRD)[14]、X-射线光电子能谱(XPS)[15]、显微红外光谱(MIR)[16]等，这些方法都是以组分直接混合后体系的性能变化来评估其相互作用，这可为新型含能材料的开发奠定坚实的基础，但并未涉及分子间的作用本质。而且从实验的安全角度来说，含能材料的实验研究成本较高，且在其生命研究周期内始终存在安全隐患。另外，固体推进剂在创制、固化降温、加工、运输、使用及贮存等过程中承受温度、加速度、振动、点火冲击等多种载荷，推进剂内部会产生应力应变，可能出现微裂纹、微孔洞，甚至出现裂纹、变形等缺陷，从而使推进剂产生损伤，这将导致推进剂装药或发动机性能严重恶化，甚至发生爆炸事故。

近年来，随着计算机和模拟技术的不断发展和完善，利用计算机模拟技术研究固体推进剂的性能日益受到国内外研究者的广泛关注。采用计算机数值模拟不仅可以比较、验证多种近似理论，还可对实验和构建的模型进行比较，从而实现含能材料的性能预估。另外，某些参数可能无法或难以用实验测试，而这些参数一定程度却可以通过计算机数值模拟被精确地计算出来，从而为实验研究提供可靠的理论依据。推进剂的多尺度模拟可从微观、细(介)观和宏观等多个尺度揭示其结构与性能之间的关系(构效关系)，这不仅有利于新型推进剂的配方理论设计，还可明显缩短推进剂的开发周期，并提高推进剂研究过程的安全性[17-18]。基于以上分析，本文围绕固体推进剂力学损伤的模拟方法，从微观分子动力学、介观耗散动力学，细观和宏观多尺度论述了固体推进剂损伤的研究进展，提出了用模拟方法研究固体推进剂损伤的思考和建议。

2 微观分子动力学模拟

分子动力学(molecular dynamics，MD)模拟是运用经典力学和力场发展起来的一种联系微观世界与宏观世界的强有力的模拟计算方法。该方法可从微观尺度评估含能材料的相容性、结合能、内聚能密度等特性，这不仅为实验提供理论指导，还可大幅节省时间和费用，在微观体系的相互作用探究方面具有独特的优势[19]。固体推进剂是以高聚物为基体，高固体颗粒填充的复合含能材料，采用分子动力学模拟方法研究推进剂组分间的相互作用通常可从共混体系和共晶体系两方面展开。

2.1 共混体系

共混体系是推进剂中两组分通过物理混合，研究其相互作用，多见于含能黏合剂/含能增塑剂体系或含能黏合剂/含能填料体系。对于含能黏合剂/含能增塑剂体系，含能黏合剂如缩水甘油叠氮聚醚(GAP)、聚缩水甘油醚硝酸酯(PGN)、硝化棉(NC)等，含能增塑剂如硝化甘油(NG)、二缩三乙二醇二硝酸酯(TEGDN)、丁基硝酸酯基乙基硝胺(Bu-NENA)等。如文献[20]用MD研究了PGN与癸二酸二辛酯(DOA)、癸二酸二异辛酯(DOS)、邻苯二甲酸二丁酯(DBP)的混溶性，计算了内聚能密度、溶度参数和结合能，并得到了各组分及共混体系的平衡构象。赵昱等[21]用MD方法研究了GAP黏合剂与双(二硝基丙基)缩乙醛/缩甲醛(BDNPF/A，A3)、Bu-NENA和TEGDN的相容性，发现这3种增塑剂与GAP的混溶过程均放热，且3种增塑剂均可与GAP相容。于艳春等[22]用MD计算了GAP/NG/BTTN(丁三醇三硝酸酯)/DNOAF(二硝基偶氮氧化二呋咱)、GAP/NG/BTTN/AlH、PEG/NG/BTTN/DNOAF和PEG/NG/BTTN/AlH3四种多组分混合体系的性能，发现AlH3和DNOAF与黏结剂的结合能较大，表明两者的相容性较好，PEG/NG/BTTN/AlH3体系力学性能更好。齐晓飞等[23-24]用MD方法计算了NC/1,5-二叠氮基-3-硝基-3-氮杂戊烷(DIANP)、NC/NG、NC/聚乙二醇(PEG)和NC/Bu-NENA等共混体系的力学性能、结合能及其分子间的径向分布函数，发现在NC/DIANP体系中，DIANP降低NC刚性、增强其塑性的效果比NG更显著；且NC/DIANP共混体系的力学性能与结合能有关，结合能大的模量高，结合能小的模量低，与DIANP和NC间有强的相互作用有关。在NC/NG体系中，NC分子链的回转半径随温度升高而增大的趋势不明显，而随NG分子数量的增多而增大的趋势十分明显。在NC/PEG体系中，NC与PEG分子间存在较强的相互作用，PEG以碎晶的形式分布在共混体系中。而且与NG相比，Bu-NENA加快了NC的溶塑速率，增加了体系的自由体积，增强了NC分子链内部的作用力，增大了溶塑产物的最大伸长率和最大拉伸强度。图1展示了NC、NG和DIANP及其共混体系模型[23]。

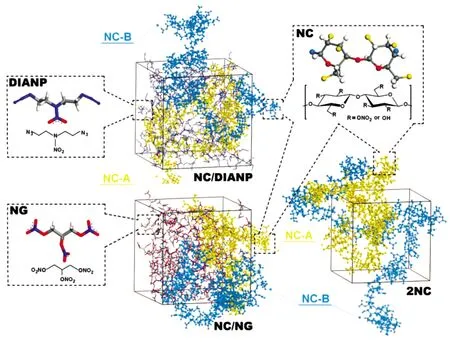
图1 NC、NG和DIANP及其共混体系模型示意图Fig.1 Models of NC，NG，DIANP and their blends

当共混体系中存在较强的分子间氢键作用时，通过结合能、径向分布函数和玻璃化转变温度可评估黏合剂与增塑剂的相容性。蔡贾林等[25]用MD研究了端羟基聚醚(HTPE)与DBP、DOS和邻苯二甲酸二乙酯(DEP)的相容性及HTPE/增塑剂共混体系的玻璃化转变温度(Tg)。通过温度—比容关系得到HTPE与3种增塑剂相容性的优劣顺序为：[HTPE/DBP]>[HTPE/DOS]>[HTPE/DEP]。

对于含能黏合剂/含能填料体系，如肖继军等[26]用MD研究了HMX/含氟聚合物形成的高聚物黏结炸药(PBXs)性能，计算了TATB与氟聚物之间的结合能，发现HMX/氟聚物体系的弹性系数和模量比HMX低，表明混合体系的刚性减弱，且黏结剂组分的加入有效地改善了HMX的力学性能，但同时或多或少地降低了HMX的爆速和爆热。马秀芳等[27]用MD研究了TATB基氟聚物PBXs的力学性能，发现随着氟聚物浓度的增大，PBXs的弹性系数和模量均减小，而结合能增大；同时，随着温度的升高，PBXs的刚性和结合能减小，而弹性增大。许晓娟等[28]用MD计算了ε-CL-20与聚氨基甲酸乙酯(Estane5703)、GAP、端羟基聚丁二烯(HTPB)、PEG和F2314组成PBXs的结合能和相容性，发现PEG与ε-CL-20的结合能最大，相容性最好；HTPB对ε-CL-20力学性能的改善最明显，且HTPB/ε-CL-20的感度最低，而F2314对ε-CL-20消极能量影响最小。屈蓓等[29]用MD研究CL-20与推进剂主要组分间的相互作用。发现CL-20与黑索金(RDX)、奥克托今(HMX)混合体系的引发键N-NO2键最大键长(Lmax)随温度的升高显著增大，导致其更易断裂、分解；而CL-20与NC、NG共混体系的键长相对变化不大，表明CL-20与NG、NC键混合后的稳定性增加，不易发生键的断裂和分解。

以上通过MD模拟方法可有效地计算不同增塑剂对含能黏合剂的增塑效果，含能黏合剂对含能填料力学性能的改善，可为新型含能黏合剂或含能增塑剂的开发与创制及应用的实验研究提供有效可靠的理论基础。

2.2 共晶体系

共晶是一种新的改性技术，是将2种或2种以上不同种类的分子通过分子间非共价键(氢键、离子键、范德华力和π-π键等)及空间效应来影响超分子网络的形成，微观结合在同一晶格中，形成具有特定结构和性能的多组分分子晶体[30]。

国内外报道的多见于如何降低CL-20、HMX等高能高感度炸药的研究。例如卫春雪等[31]研究了HMX/TATB共晶体系的结构与性能，发现HMX的5个主要生长面，TATB在比表面能越小、生长速度越慢的晶面上取代形成的共晶能量越低，结构越稳定。林鹤等[32]研究了HMX/FOX-7共晶体系的结构与性能，预测了共晶形成的可能性，HMX/FOX-7共晶在(0 2 0)晶面上结合能最大，体系能量最低，更加稳定，有利于HMX/FOX-7共晶的形成。武宗凯等[33]研究了CL-20/FOX-7共晶的形成，计算了共晶体系的分子间相互作用，发现FOX-7与CL-20分子间存在较强的氢键和范德华力，且CL-20/FOX-7共晶模型中的(1 0 1)晶面的结合能最大。陶俊等[34]构建了CL-20/HMX共晶模型，模拟了CL-20/HMX的共晶体系的力学性能、结构稳定性及径向分布函数，并与共混体系进行了对比，发现CL-20/HMX共晶能显著改善体系的抗形变能力及延展性。共晶结构的弹性模量明显大于共混结构，Cl-20/HMX共晶体系的CED值远远大于CL-20/HMX共混体系的值。可知，对于温升导致结构不稳定的程度ε-CL-20大于β-HMX的，且CL-20/HMX共混和共晶结构的Lmax值相差很大，表明共晶能使得体系结构稳定性增强，起到“钝化”的作用；共混减弱了体系的稳定性，起到了“敏化”的作用。

因此，基于共晶原理，将具有高能特性的炸药分子与具有低感特性的炸药分子在分子水平上实现相互间的非共价键作用，形成拥有独特结构，同时具有高能低感特性的共晶炸药，为解决现有单质含能材料能量和安全性矛盾，新型高能钝感含能材料的开发，提高武器弹药高效毁伤能力和安全性提供了一条新途径[30]。

3 介观耗散动力学模拟

介观耗散动力学(meso dissipative dynamics，DPD)从20世纪90年代初由Hoogerbrugge和Koelman首次提出，是在分子动力学和格子气模拟的基础上发展起来的。耗散粒子动力学采用粗粒化模型，它将实际流体中的一小块区域或包含大量分子或原子的团簇看作耗散粒子动力学模型的一个作用点。由于耗散粒子动力学在粒子间引入了“软”的相互作用势，从而有效模拟时间和空间尺度介于微观尺度与宏观尺度之间的体系，并给出体系的结构形貌、粒子数密度分布、扩散系数、表面张力等宏观性质。耗散粒子动力学已被广泛地应用在高聚物熔融体、高分子溶液等体系的研究中，已有部分应用在含能材料领域[35]。如Gee等[36]将耗散粒子动力学方法应用到含能体系中，利用经典分子动力学方法模拟了实验观察不到的TATB颗粒的“不可逆长大”。这一创举不仅拓展了耗散粒子动力学在含能体系中的应用，而且还突破了以往在微观尺度和宏观尺度上研究含能混合体系的局限性，这对于发展含能体系在介观尺度上的研究具有重要的历史意义。

2008年，张艳丽等[37]用耗散粒子动力学对4种TATB基PBXs的介观结构及其演变过程进行了研究，发现聚合物在单质炸药TATB中形成线形的网状结构；随着聚三氟氯乙烯重复单元在聚合物中含量比例的增加，聚合物在TATB中的扩散越来越容易；温度升高也会使更多的聚合物扩散到TATB中，且聚合物在400 K时形成蜂窝状结构，能很好地包覆TATB。齐晓飞等[38]用Meso Dyn模拟方法对比了NC与DIANP、Bu-NENA、BDNPF/A和NG共混体系的相结构、演变过程及影响因素，发现相对于NG，DIANP溶塑NC速率较快，且2种共混体系的微观形貌与介观动力学模拟结果相一致。图2是NC/增塑剂共混体系的有序度参数、介观形貌(a)和扫描电镜照片(b)[38]，其中，共混体系的介观形貌用红色表示NC相、绿色表示增塑剂相。由图2(a)可知，与NG相比，DIANP、Bu-NENA和BDNPF/A与NG的混溶性较好，它们与NC共混后体系的熵较小，共混体系没有明显的相分离产生。NC/NG共混体系中两相界面清晰，NC和NG相存在各自团聚、融合的现象，发生了相分离；而其他共混体系中增塑剂均匀分散在NC相中，两相没有发生明显的相分离，而是互相贯穿、缠绕，界面模糊，形成典型的“海-岛”式分布结构。由图2(b)可知，与NG相比，其他3种增塑剂与NC的混溶效果更好，因而混溶产物的微观形貌照片上基本观察不到NC球形药的轮廓。相比之下，NC/NG共混体系的混溶产物存在明显的球形药轮廓，与周围界限分明，表明NG与NC的混溶效果相对较差。

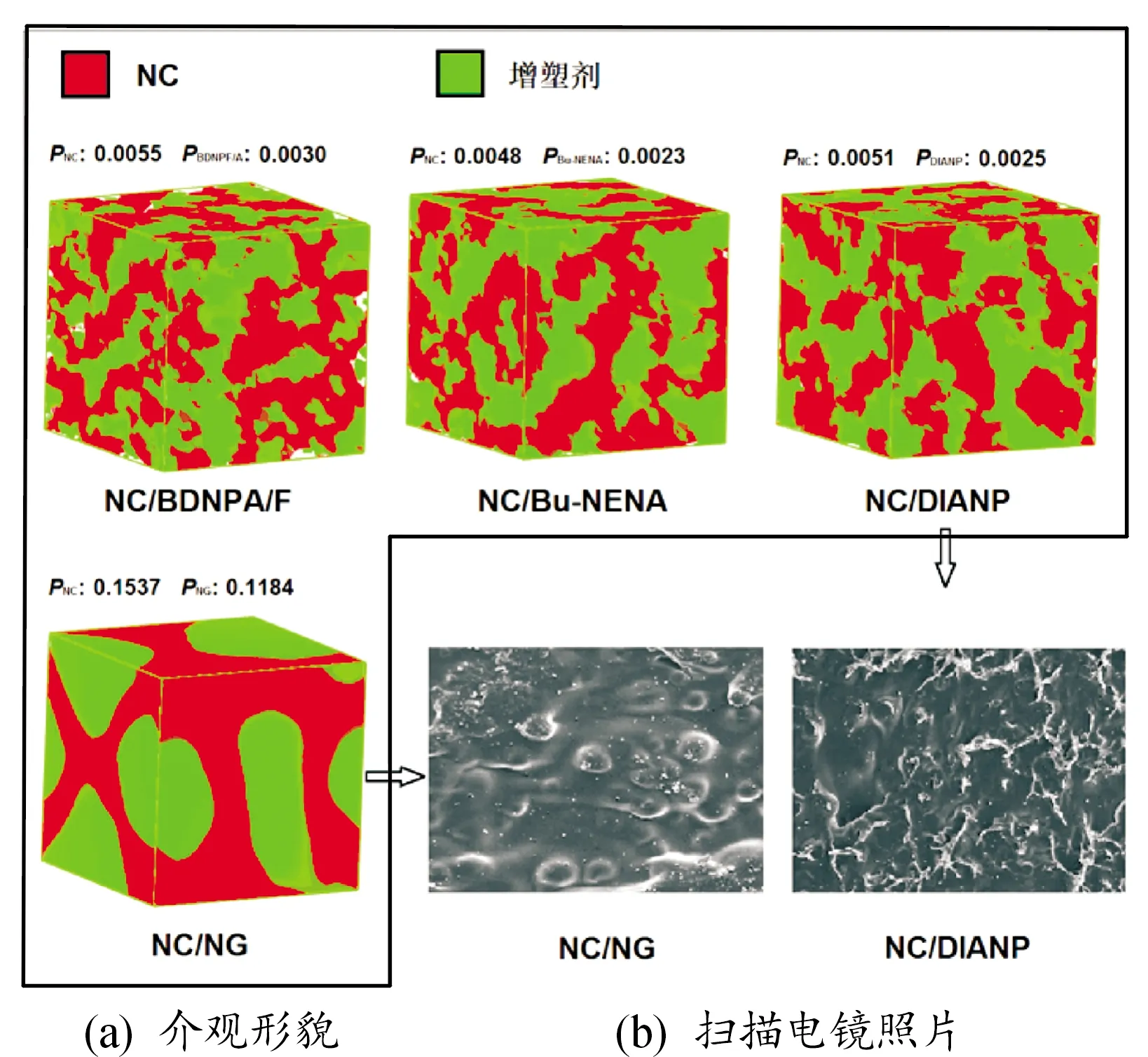
图2 NC/增塑剂共混体系的有序度参数、介观形貌 和扫描电镜照片Fig.2 The ordering parameters，mesoscopic morphology and SEM photos of NC/plasticizer mixtures

随着耗散粒子动力学理论和算法的不断改进和完善，其应用领域也越来越广泛。近年，王可等[39]用MD和DPD多尺度方法研究了不同含量三羟甲基乙烷三硝酸酯(TMETN)对硝化棉(NC，含氮量12%)的增塑效果。发现NC/TMETN质量比为1.3∶1时，体系中NC回转半径最大、氢键作用最强且力学性能最好，表明该质量比下TMETN增塑效果最好；硝酸酯键拥有较小的平均引发键键长和最小的最大引发键键长，故该质量比下体系安全性最好；表明质量比为1.3∶1体系混匀程度和混匀时间均优于1.2∶1体系，即1.3∶1体系中TMETN对NC增塑效果更好。由此可知，将微观和介观尺度结合起来，用介观耗散动力学模拟可较好地作为微观分子动力学的辅助手段。

4 细观损伤模拟

对于固体推进剂细观损伤和裂纹扩展研究，大多采用实验测试手段，如单轴拉伸/压缩[40]、扫描电子显微镜[41]、声发射技术[42]、超声波技术[43]、数字图像处理技术[44]及核磁共振成像技术[45]等。这些研究方法都只是从宏观尺度研究固体推进剂的力学性能，而推进剂的宏观力学性能是由推进剂的微细观结构决定的。为了进一步揭示推进剂的力学损伤机演化机理，采用数值模拟技术建立固体推进剂的细观结构模型，研究推进剂在不同载荷下细观损伤的萌生及演化机理已成为主要技术手段，而且，这些模拟研究技术可为推进剂实验研究奠定坚实的基础[46]。

细观力学有限元方法将有限元计算技术与细观力学和材料力学结合，其本质是根据复合材料具体的细观结构，建立代表性体积单元(RVE)和边界条件，求解受载荷作用下RVE的应力应变，从而建立起细观局部量和宏观平均量的关系，最终获得复合材料的宏观力学性能。该方法最大的优点在于能够获得细观尺度下的应力应变来反映复合材料的宏观性能[47]。通常，黏合剂基体与固体颗粒的粘结界面的应力应变反映了推进剂的细观结构与力学性能的相关性，为了更准确地表征界面粘接性能，近年来广泛采用的方法是引入表征固体颗粒/基体界面的张开量与界面应力间关系的粘聚区模型(CZM)。在CZM中，常用的有双线性、多线性、指数型和多项式等，其中双线性界面粘聚区模型应用较广泛。如2013年，李高春等[48]在复合推进剂的黏合剂基体与颗粒间引入了粘结界面单元，采用双线性模型描述其界面损伤及扩展特性，并对推进剂内部的细观界面脱粘过程进行了有限元分析；发现采用粘结界面单元可有效地模拟推进剂基体/颗粒的界面脱粘过程，且模拟结果与试验结果相吻合。接着，封涛等[49]基于分子动力学的颗粒填充算法构建了HTPB推进剂的细观结构模型，在HTPB/AP基体界面处引入界面粘接接触单元，获得了HTPB基体与AP颗粒界面粘接处的损伤(裂纹)萌生、扩展至宏观裂纹的破坏过程。图3展示了HTPB推进剂的细观填充结构模型[49]。对比发现，损伤内聚力模型能准确地表征推进剂在单轴拉伸过程中HTPB基体与颗粒界面之的间脱黏(脱湿)过程，模拟结果与实验结果的偏差≤10%，从而验证了所构建的细观模型的可靠性及反演所得界面参数的准确性。

图3 推进剂细观模型网格划分及边界条件示意图Fig.3 Mesh generation of propellant meso-scale model and boundary condition

为了对模拟结果进行验证，职世君等[50-51]用表面粘结(Surface-based Cohesive)方法研究了固体推进剂的黏合剂基体/固体颗粒间界面损伤，计算了界面的损伤参数及对推进剂最大延伸率的影响，同时还建立了异质型复合推进剂的细观结构模型，并引入移位因子来体现界面损伤的非线性力学特性。发现随着AP含量的增加，推进剂的最大延伸率减小，形成的宏观裂纹越明显，且界面损伤多从大颗粒附近出现，这和文献[43,48]中研究结果相吻合。

图4为推进剂在不同载荷条件下单轴拉伸过程的细观损伤照片[52-53]。从图4(a)可以看出，随外界拉伸载荷的增加，基体与颗粒界面间产生微裂纹，进一步增大载荷，微裂纹不断扩展。由于界面出现脱粘现象，颗粒在界面脱粘处不再承受应力，使其附近区域的基体在较大载荷作用下产生微裂纹。随着载荷的进一步增大，微裂纹集中，导致宏观裂纹的形成，进而使推进剂遭受破坏。从图4(a)可以看出，基体的变形总体上比颗粒的变形大，其中上半部分整体向上移动，下半部分整体向下移动，在基体中间出现较大左右移动。

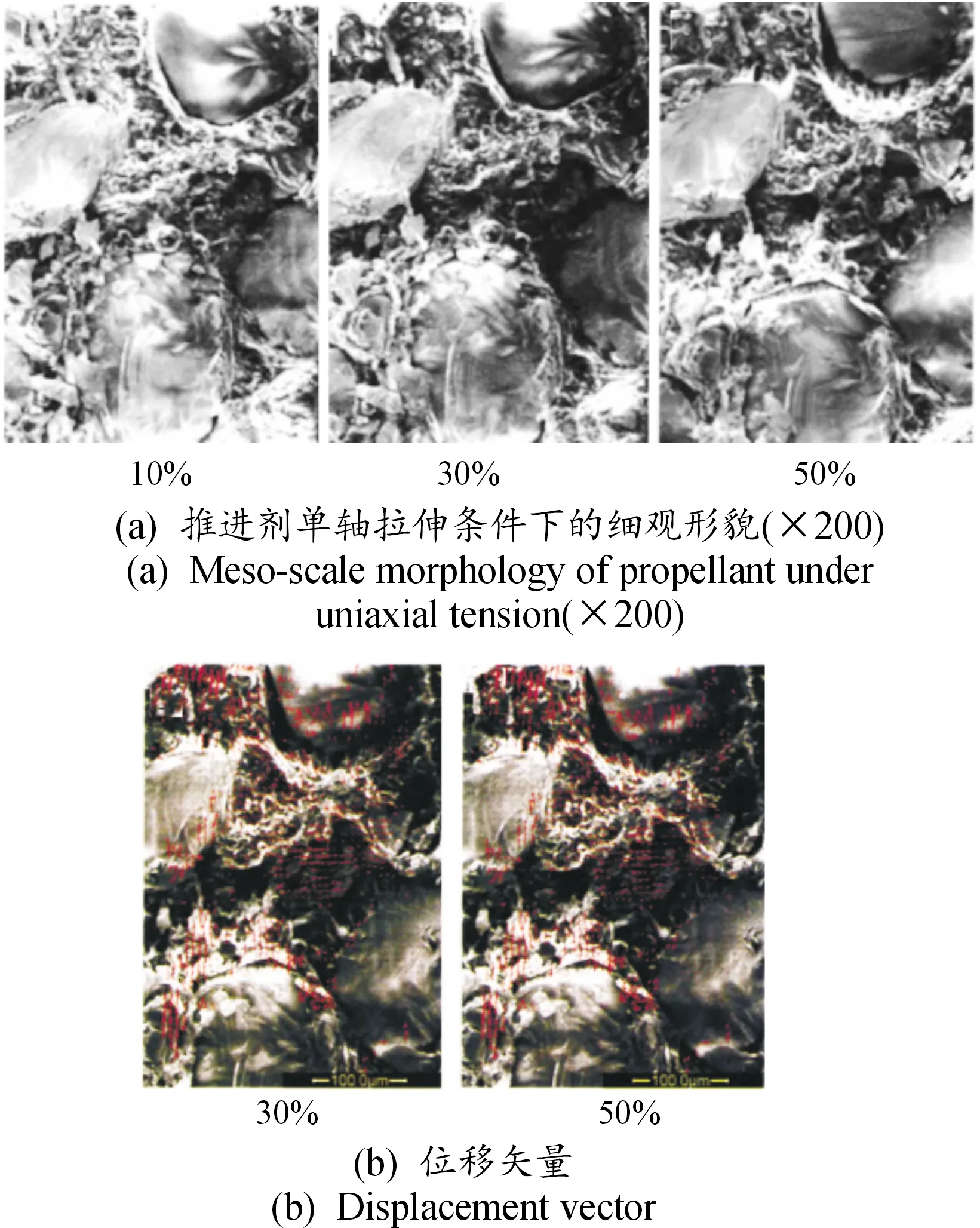
图4 不同载荷下拉伸过程的细观损伤照片Fig.4 Comparison of meso-scale damage simulation and experiment in tensile process under different loads

基于粘结界面单元的引入，史佩等[52]建立了二维颗粒填充模型，用双线性界面力学模型对复合推进剂的界面脱粘进行了分析，得到了细观结构的Mises应力应变分布。韩波等[53]用双线性粘聚区模型构建了推进剂裂纹扩展过程的物理、数学模型，获得了裂纹尖端损伤的应力场分布及裂纹扩展方式。曲凯等[54]基于界面内聚力粘结模型，用Mori-Tanaka方法研究了非线性界面脱粘对推进剂力学性能的影响。发现固体颗粒的大小、体积分数和基体/颗粒间界面粘接强度对推进剂的力学性能有明显影响，内聚力粘接模型可有效评估推进剂基体/颗粒间的脱粘过程。同时，Tan等[55]将Mori-Tanaka方法扩展应用到单轴拉伸载荷作用下的颗粒增强复合材料，发现当颗粒尺寸小于临界尺寸时，这些小颗粒起着强化基体力学性能的作用，而当超过这一临界尺寸时，颗粒的脱粘会导致出现应力软化行为。为了进一步了解颗粒增强基体的力学行为，文献[56-57]构建了率相关粘聚区模型，通过实验的反演识别方法确定了粘聚区参数，分析了推进剂的裂纹扩展和界面脱粘失效行为，可为推进剂的力学性能及损伤失效提供技术借鉴。

在固体推进剂力学损伤研究过程中，为了获得可压缩基体和近似不可压缩AP颗粒的力学行为，Matous等[58-59]将小颗粒与黏合剂黏合剂体系视为均匀化的基体，采用指数型界面粘聚区模型研究了颗粒的界面脱湿的演化过程，实现了基体和基体/颗粒间界面扩展的非均匀应力和变形场的有限元计算，并用堆积算法研究了双尺寸颗粒堆积模型中颗粒脱湿对推进剂宏观力学性能的影响。发现通过粘超弹性复合含能材料粘聚区模型的引入，可更精确化模拟推进剂的细观损伤，实现颗粒增强弹性体在有限变形下多尺度模拟研究宏观颗粒的脱湿萌生、扩展、演化过程及失效的微细观机理。同时，借助数学图像处理方法，刘著卿等[60]通过提取出大颗粒的几何模型，对HTPB推进剂以0.4 mm/min的等速率单向拉伸用双线性界面本构关系进行拉伸载荷下的界面脱粘模拟，预测出推进剂细观损伤的萌生与扩展过程，这些都为联系推进剂损伤的宏观尺度与细观尺度机理迈进了坚实的一步。典型的颗粒填充复合材料在拉伸载荷作用下的微细观损伤如图5所示。

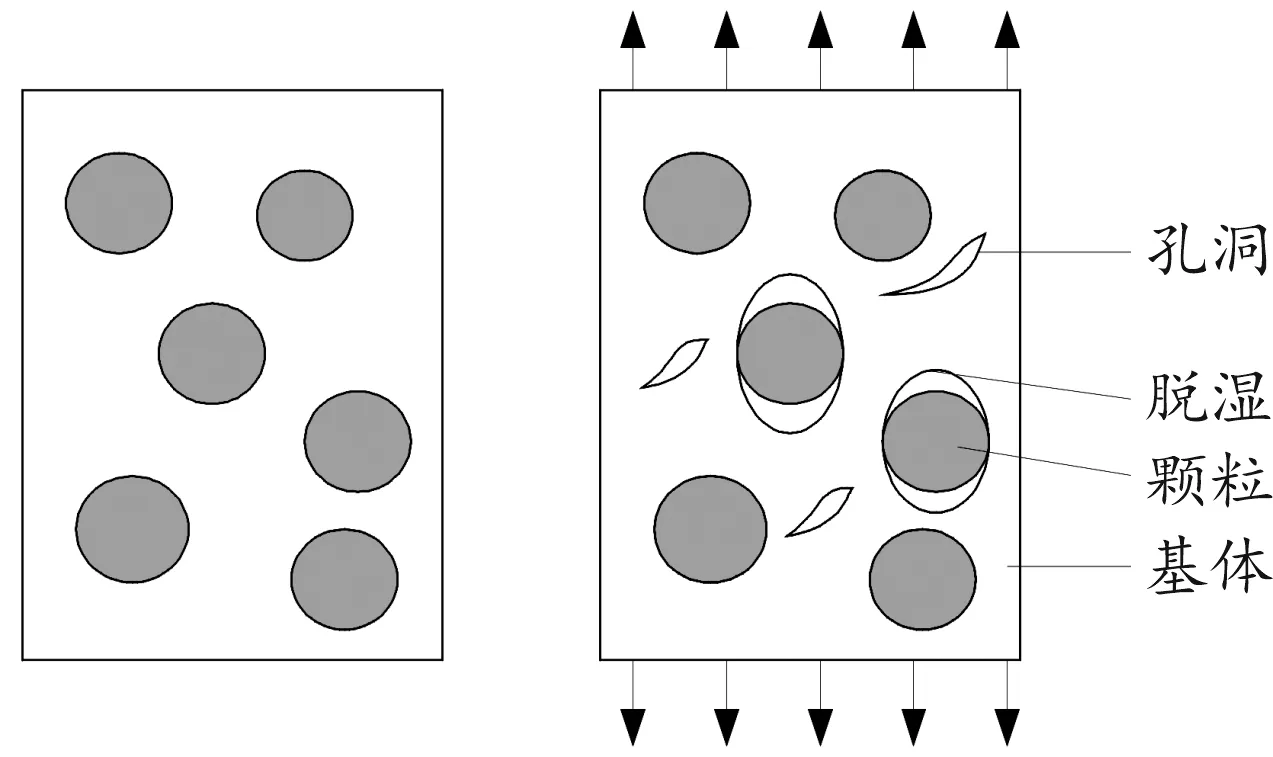
图5 典型的颗粒填充复合材料在拉伸载荷作用下的 微细观损伤示意图Fig.5 The Micro damage diagram of typical particle filled composites under the tensile load

文献[61-62]引入泊松比，将AP颗粒当作线弹性体，黏合剂基体设定为Odgen超弹性本构模型，建立预测界面微裂纹的单颗粒三维胞元有限元模型，通过对三维胞元模型的有限元计算得到不同颗粒含量时(15%、30%和45%)3种界面状况下(界面粘结完好、部分脱粘以及完全脱湿)推进剂的泊松比变化，并对不同体积分数不同脱粘状态下的界面强度进行对比，发现颗粒的体积分数越大，泊松比降低地越多，泊松比可较好地反映出脱湿引起的体积膨胀。另外，彭威和李敬明等[63-64]在建立复合推进剂球形颗粒填充正六方体的有限元计算模型的基础上，研究了不同尺寸的填充颗粒在相同应变下的应力大小及分布,发现在颗粒的极区处通常首先出现微裂纹扩展，且大颗粒界面处的应力明显大于小颗粒的，界面/颗粒间的脱湿是主要损伤形式，这为预测颗粒在粘接单元最先出现界面脱粘及破坏的形式及趋势。

总之，推进剂细观尺度的损伤模拟是联系推进剂宏观尺度损伤破坏和微观裂纹萌生的纽带。通过在基体/颗粒间界面的粘聚区模型的引入和构建及优化，可有效预估固体推进剂在不同载荷条件下损伤出现的时机和位置，分析应力的分布和大小，这也是研究推进剂宏观力学失效与微观机理的关键所在。

5 宏观性能模拟

固体推进剂药柱作为固体发动机的能量来源，其在制造、贮存、运输和使用过程中，受热、冲击、振动、加速度和点火压力等载荷的作用下都会引起推进剂药柱损伤、发动机工作异常等。因此，为了使固体发动机能够正常工作，要求推进剂必须具有非常好的力学性能以承受在发射和运输过程中所产生的巨大应力以及在生产和长期贮存期间温度变化所产生的热应力，保证推进剂结构的完整性。由于固体推进剂组分较多，相互作用关系复杂，因此其力学性能影响因素较多，使得复合固体推进剂力学行为的模拟及预估计算难度大，计算精度需进一步提高[65-66]，因此，建立固体推进剂的本构模型和有限元分析尤为重要。

5.1 本构模型法

在推进剂装药的设计过程中，必须保证推进剂装药结构的完整性，这就需要建立相应推进剂的粘弹性本构模型，以此为基础，对推进剂装药在点火、温度骤升/骤降等载荷下的力学相应进行有限元仿真分析[67]。因此，建立准确的推进剂本构模型是固体推进剂设计与仿真的基础。通常，国内外提出的相关本构模型有广义Maxwell模型[68]、非线性ZWT模型[69]、基于Yeoh函数超弹模型建立的一种粘弹本构模型[70]等。如文献[71-72]依据HTPB推进剂和改性双基推进剂在损伤过程中伴随着细观裂纹的形成和能量的释放过程，用累计损伤模型建立了HTPB推进剂的损伤本构模型和改性双基推进剂的损伤本构模型。邓凯等[73]组合Schapery和Perzyna粘塑性本构模型模拟了HTPB推进剂的粘弹塑性本构模型。沙宝林等[74]使用唯象学统一本构对装药在点火压力载荷下的力学响应进行了有限元仿真分析。

另外，基于三相结构模型(分散相-界面相-连续相)，田德余等[75]建立了推进剂力学性能参数与黏合剂基体的伸长率和弹性模量、推进剂组分固体含量、粒径、级配、黏合剂和键合剂等的数学关系，预估了丁羟推进剂的力学性能，得出的推进剂抗拉强度和伸长率的计算结果与实验值吻合较好。贵大勇等[76]将颗粒填充聚合物三相结构(颗粒相-中间相-基体相)和粘弹模型相结合，构建了NEPE推进剂的三相结构粘弹模型，建立了NEPE推进剂力学性能参数与其配方组成、固体填料粒径及级配、黏合剂基体的拉伸强度和模量等参数的数学关系，结果表明90%的算例中推进剂拉伸强度和伸长率计算值与实验测试结果相对误差小于20%。文献[77]基于Christensen和Lo的三层球模型提出了二层嵌入模型，较好地模拟了颗粒填充高分子复合材料的拉伸强度。上述研究都是对推进剂力学性能预估的有效开拓和补充。

5.2 有限元方法

有限元方法是根据所研究材料具体的细观结构，建立代表性体积单元(representative volume element，RVE)和边界条件，求解受载荷作用下RVE的应力应变，根据所获得的应力应变分析材料的实际损伤过程。Mori-Tanaka方法由于运算简单，广泛地用于复合材料的有效模量预估。例如李高春等[78]采用细观力学有限元法和Mori-Tanaka分析法相结合的方法计算了推进剂的模量，计算所得模量与不同颗粒体积分数推进剂的单向拉伸试验结果吻合。Gdoutos[79]对固体推进剂裂纹的萌生和扩展进行了有限元计算，用Ogden超弹性本构方程计算了裂纹尖端的应力场，并预测了裂纹扩展行为。发现裂纹起始和非稳定扩展的临界位移以及裂纹张开位移受试件的几何形状和裂纹长度影响。即使在较小位移作用下，裂纹尖端附近将产生大变形，并在最终断裂前存在稳定的裂纹扩展。为了检验模拟的有效性和可靠性，强洪夫等[80]用材料试验机和分离式霍普金森压杆(SHPB)对双基推进剂进行了单轴压缩实验，用含损伤朱-王-唐(ZWT)本构模型对实验结果进行了拟合，得到了模型中的本构参数。通过模型预测曲线与实验曲线的对比，发现双基推进剂具有明显的应变率相关性，动态下屈服应力与静态下相比明显提高，且含损伤ZWT本构能较好地描述双基推进剂在0～0.14应变范围内的力学损伤特性。

图6是某HTPB推进剂拉伸过程中变形有限元仿真与实验照片[81]。可以看出，由于内孔处存在应力集中效应，Mises应力在内孔处最大，且随着拉伸载荷的增大，试样中的最大应力值也随之增大。

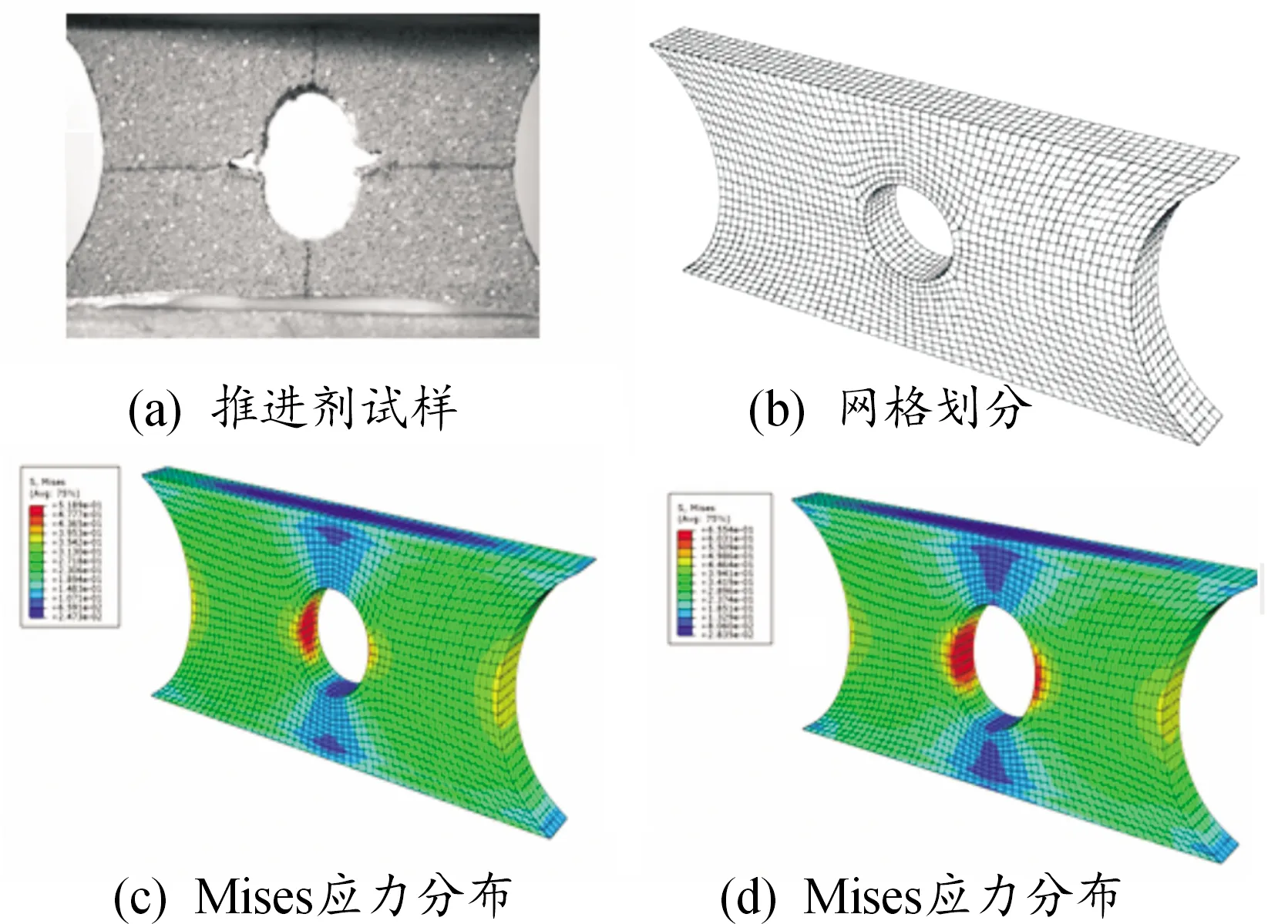
图6 HTPB推进剂拉伸过程中变形仿真与实验照片Fig.6 Simulation and experiment of HTPB propellant deformation in tensile process

宏观力学损伤模型虽可以考虑推进剂的损伤对其力学性能的影响，可用于判断推进剂的破坏与否，但宏观力学模型还需进一步完善，须考虑推进剂的实际组成及在拉伸过程中推进剂内微裂纹的起始和成核进而产生断裂的过程。

6 固体推进剂力学性能数值模拟的建议

通过以上论述和分析可知，数值模拟的优势在于：一方面，可以节省大量的人力、物力和财力，缩短新材料的创制周期，降低开发成本；另一方面，还可以提供在极端条件(辐射、超高压和超高温)下的“实验数据”，代替一些很难或根本不可能实际试验测试完成的研究。因此，数值模拟结合理论分析和实验研究已成为现代科学研究的3种主要方法(图7)[82]。数值模拟在实验测试的基础上，通过理论分析，构建相应的本构模型和方程，通过最优算法对方程进行数值计算或求解，从而计算出符合实验测试的结果和性能。计算机数值模拟可以弥补理论分析和实验研究的不足，既可对实验结果进行预测，提供分析实验结果的理论基础，又可提供与理论分析相比较的模拟数据，验证分析结果的准确性和可靠性。计算机数值模拟已逐渐成为联系理论分析和实验研究之间的一座重要的桥梁。相信随着更高性能计算机的出现及力场、计算方法等力学理论的深入研究，通过理论与实验研究紧密结合，数值模拟方法必将成为研制高性能固体推进剂不可或缺的技术手段[83-84]。

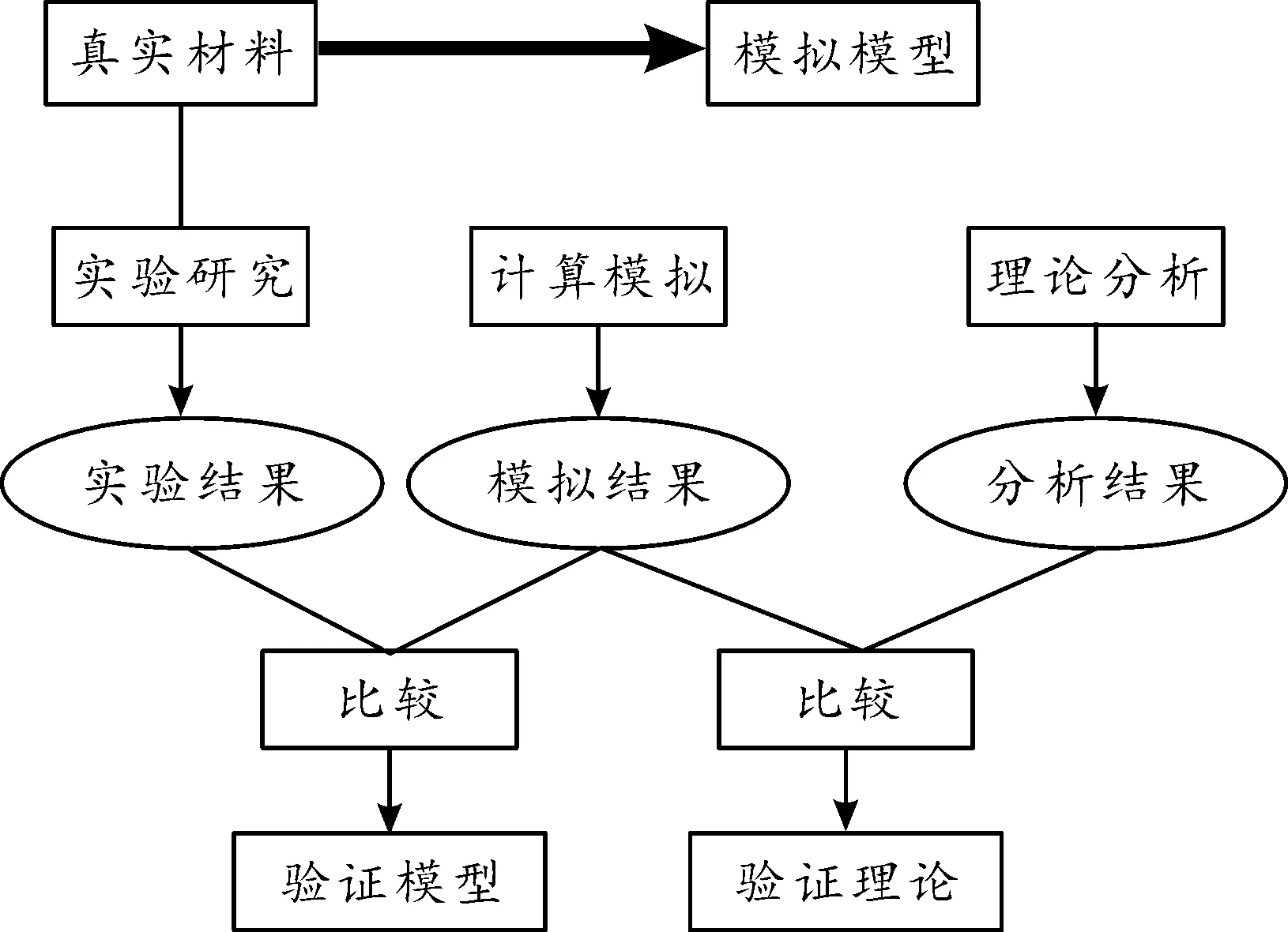
图7 理论分析、数值模拟和实验研究之间的关系Fig.7 The relationship between theoretical analysis， numerical simulation and experimental research

固体推进剂细观尺度的损伤模拟是联系推进剂宏观尺度损伤破坏和微观裂纹萌生的纽带(图8)，对固体推进剂细观裂纹的萌生、扩展和演化机制的研究发展方向主要有：① 优化微细观模型与算法，提高模拟的速度和精度，减少耗时；② 进一步建立数值仿真与实验的相关性和一致性，建立可靠的、精确的推进剂组分和细观结构模型，更加深入研究裂纹萌生、扩展及演化中的机理问题；③ 拓展固体推进剂的微观结构与其宏观性能之间内在关系的研究，通过将低尺度的模拟结果转化为高尺度模拟的输入参数，初步实现了微观-介观-宏观多尺度连贯研究；④ 继续推进多尺度计算机模拟方法的贯通和发展。随着推进剂结构性能研究的深入，从微观到细观(介观)再到宏观研究的多尺度贯通的量传问题亟待得到解决[85-86]。

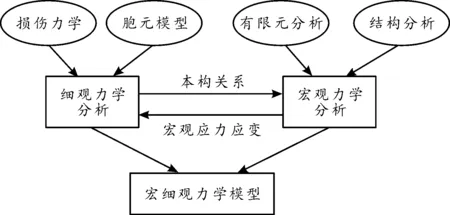
图8 推进剂宏细观力学模型关系框图Fig.8 Relationship between macro and meso mechanical models of Propellants

7 结论

1) 通过分子动力学微观和推进剂细观损伤模拟，可弥补宏观尺度实验研究手段的不足，有助于深入揭示推进剂的结构与性能之间的内在构效关系，且采用微观-细观-宏观多尺度模拟方法不仅能大幅缩短研制周期，降低成本，还可明显提高推进剂研究过程中的安全性。

2) 分子动力学模拟具有沟通固体推进剂的宏观特性和微观结构的作用，对于难以了解的现象可做出一定的微观解释。

3) 通过微观-细观(介观)-宏观多尺度模拟有效链接可系统研究固体推进剂的力学损伤，为进一步揭示损伤机制提供理论指导。