磁浮列车雷击接地模型及其多气隙击穿特性研究*

杨宗元，张健穹，王庆锋，李相强

（西南交通大学 物理科学与技术学院，成都 610031）

磁浮列车是基于电磁力悬浮于轨道的新型高速列车［1］，在空旷地带高速行驶时，有遭受到直击雷的风险。由于磁浮列车特有的供电系统，故其防雷特性与动车组列车、飞行器和建筑物均有所不同。首先磁浮列车上方没有类似动车组接触网的供电结构，在雷雨环境下车体没有额外的地面雷击防护措施。其次磁浮列车高速行驶时车体与地面的轨道处于悬浮状态，没有可见可预计的大电流接地路径。最后由于车体和轨道存在一个短距离的气隙，因此车体遭受雷击后，车体与轨道之间的气隙会被雷电流击穿而形成泄流通道［2-3］。目前对于雷击的防护措施主要通过可靠引流使其进入大地，从而达到避免防护对象遭受雷电直接作用的目的，因此对于磁浮列车的泄流通道及其特性的研究十分重要。基于磁浮列车独特的接地系统，必须对雷击事故做出有针对性的预防，以提高磁浮列车的安全性和可靠性，因此，有必要对雷击磁浮列车的气隙泄流特性开展研究。

国内外对于雷击效应的研究主要在轮轨列车、高空飞行器和地面建筑物等方面。以动车组列车为代表的传统轮轨列车采用接触网供电，受电弓与车体之间安装有浪涌保护器。雷电的首要作用对象为接触网，当雷电流通过接触网和受电弓到达车体后会通过轮轨进入地面轨道，在这一过程中会导致列车车体对地电位上升，形成雷击车体过电压［4］。雷击车体过电压具有幅值高、上升快的特点，严重影响了车内电气设备的安全，危及列车的正常运行［5］。为了抑制雷击车体过电压，国内外学者对车体接地系统做了相关研究，并提出一系列措施提高列车的雷击防护能力［6-9］。对于高空飞行器，其雷击效应及雷击防护的研究主要为直接效应和间接效应，直接效应主要在于通过建立模型和数值仿真确定了飞行器表面各区域对于直击雷作用的风险概率，间接效应主要研究雷电流引起的电磁场分布及其对机上各设备和元件的影响，并通过缩比试验的方法形成了许多重要成果［10-11］。在地面建筑物方面，国内外学者主要通过电路方法和电磁场方法开展了雷电防护系统等效模型及雷电瞬态现象求解方法［12-13］。由于高速磁浮列车的特殊性，对于传统轮轨列车、高空飞行器和地面建筑物的雷击预防措施无法直接用于磁浮列车。同时，针对于磁浮列车雷击效应的研究较少，相关的雷击防护研究还没有形成系统性结论。因此，阐明磁浮列车雷击泄流机理，建立适用于磁浮列车的分析模型，研究抑制雷击车体过电压的方法对于提高磁浮列车在雷电环境下的安全性和可靠性是十分有意义的。

基于国内外相关雷击防护的研究方法，针对磁浮列车开展了雷击车体泄流特性的基础性研究工作。采用了基于Simulink仿真软件的集总参数电路的建模方式，搭建了磁浮列车单节车厢的雷击接地系统模型，分析了雷击车体造成多处气隙击穿从而形成雷电泄流通道的特性及其影响因素，并通过设计雷电流冲击试验平台验证了这一结论。

1 磁浮列车接地结构

磁浮列车按照悬浮机理分为电磁力悬浮型（EMS）、电动力悬浮型（EDS）和混合电磁悬浮型（HEMS），文中所研究的磁浮列车的悬浮机理为EMS中的悬浮和牵引分离型列车［14］。该种磁浮列车车体的接地结构如图1所示。该型磁浮列车采用了电磁力悬浮（EMS）的动力方式，即对车载的悬浮电磁铁通电励磁从而产生强磁场，使得悬浮电磁铁和轨道上的长定子铁芯相互吸引，将列车向上吸起悬浮于轨道上。悬浮电磁铁与支撑滑橇（TK），导向电磁铁（FM）和制动电磁铁（BM）均安装在悬浮臂中，它们分别与轨道形成一系列间距为10～20 mm的气隙。悬浮臂和列车车厢通过连接点和连接线进行等电位连接，车体两侧各有8个连接点，每个连接点有2根连接线连接相邻的2个导向电磁铁。列车通过轨道中的直线电机牵引行驶，车体的供电系统处于载客车厢下方，因此磁浮列车车体上方没有类似接触网的防雷设施。

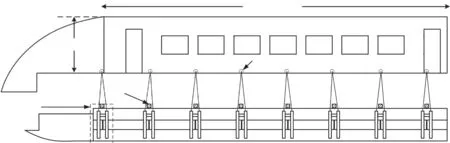
图1 磁浮列车接地结构

在磁浮列车正面侧和背面侧各有8个悬浮臂，悬浮臂的主要作用是架设长条形的电磁铁和支撑车体，每个悬浮臂与车体连接处均有1个支撑滑橇，每相邻2个悬浮臂之间安装有1个导向电磁铁，在每节车体中间位置安装有制动电磁铁，因此对于中间车，每节车共有16个支撑滑橇、2个制动电磁铁和14个导向电磁铁。

当车体遭受直击雷时，雷电流通过车体金属框架流入车体下方的悬浮臂结构，此时悬浮臂中各电磁铁与轨道之间的气隙电压迅速增大，直至气隙电压达到空气击穿阈值后产生等离子体通道，雷电流通过该等离子体通道后接入铁轨，并最终从轨道进入大地［15］。

2 雷击车体接地系统建模

多数雷击放电都在一个以上的点击中地面，雷电落点之间的空间间隔有时长达数公里［16］，由于一列常规8编组磁浮列车总长度仅200 m，相对于这个距离足够短，因此文中假定雷击点仅有1处且位于车厢前端。根据研究结果，目前工程应用中的雷电流采用电流峰值Im、波前时间τ1和半峰值时间τ2来描述，文中根据IEC 62305给出的首次雷击的电流波形进行仿真。雷击电流波形参数τ1/τ2为10/350μs，雷电流峰值Im取20 kA［17-18］，波阻抗为300Ω，如图2所示，数学模型见式（1）：

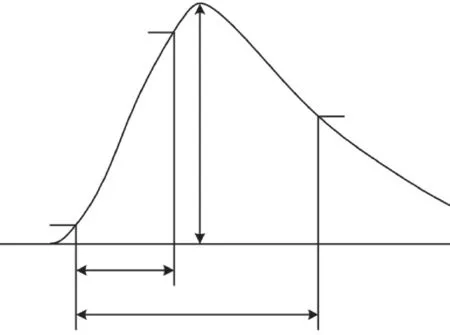
图2 雷击电流波形

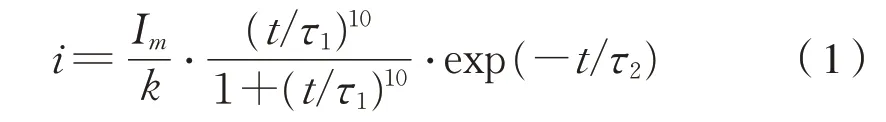
式中：Im为电流峰值；k为峰值电流的修正系数；t为时间变量；τ1和τ2分别为波前和半峰值时间常数。

单节车体的雷击接地系统仿真模型如图3所示。由于单节车厢中存在多个车体与悬浮臂的连接点，因此单节车厢等效为基于8个连接点的阻抗网络结构。文中根据该型磁浮列车车体的典型参数，利用有限元法（FEM）计算了单节车厢的金属框架阻抗，得到车厢单段阻抗Rw为0.1 mΩ，Lw为1.59μH。车厢顶部到底部的纵向电阻Rw为0.47 mΩ，电感Lw为1.49μH。利用Simulink电子电力仿真包搭建了具有分布特性的车厢阻抗等效电路。

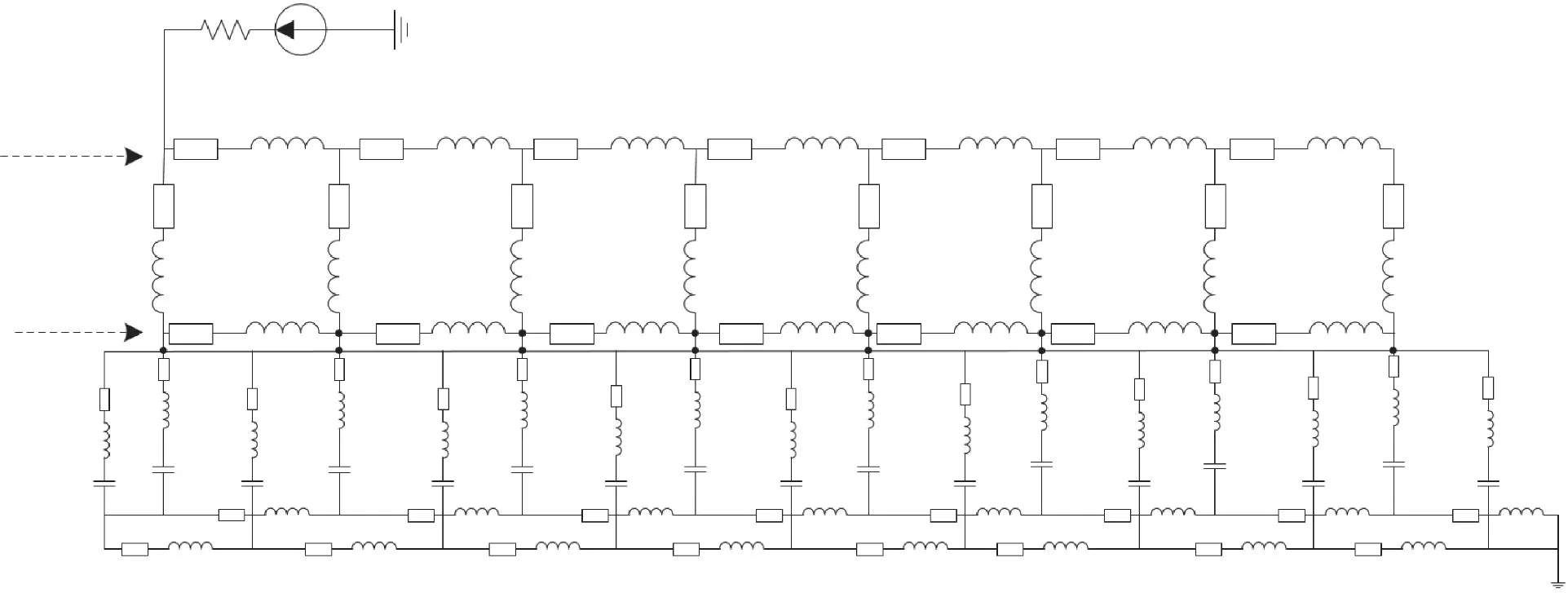
图3 雷击车体接地系统电路模型

悬浮臂通过连接线和连接点与车厢进行等电位连接，其中连接线类型为单芯铜电缆。单节车厢中相邻连接点距离约为3 m，远大于其截面尺寸和长度，因此忽略临近效应。又由于雷电流有丰富的高频分量，因此需要考虑趋肤效应。连接线的等效电感为式（2）、等效电阻为式（3）：

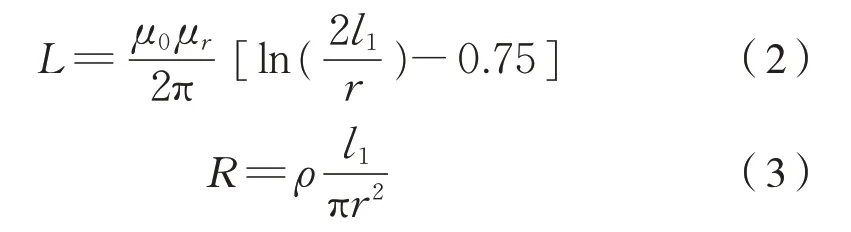
式中：r为铜芯半径；μ0为真空磁导率；μr为相对磁导率；ρ为电阻率；l1为电缆长度。

计算得到同等尺寸下导行电磁铁连接线的等效电阻Rld为0.26 mΩ，等效电感Lld为1.17μH，以及滑橇连接线的等效电阻Rls为0.08 mΩ，等效电感Lls为0.9μH。

在磁浮列车实际工作状态中，气隙的距离处于变化之中，且不同位置的电磁铁与轨道面的气隙距离也不相同。为简化分析，假定磁浮列车在高速运行时，列车各部位的气隙保持恒定。则磁浮列车电磁铁与轨道可视为距离固定的平行极板电容，其填充介质为空气，不考虑空气流动对等效电容的影响。典型的滑橇与轨道的距离为17 mm，导向电磁铁与轨道的距离为10 mm，制动电磁铁与轨道的距离为20 mm，故由极板电容公式可分别计算得到其容值为0.059、0.148、0.038 nF。采用电压控制型开关电路模拟气隙的击穿特性，当气隙电容电压达到空气击穿阈值时，气隙的阻抗特性将瞬变为低电阻，空气击穿阈值取为3 kV/mm。

单节车厢长度为25 m，选取相等长度的轨道作为分析对象，轨道简化为长直导体，其截面尺寸取列车电磁铁的截面尺寸。轨道的等效电感为式（4）、等效电阻为式（5）：

式中：l2为等效轨道长度；b为轨道宽度；c为轨道厚度。

滑橇轨道和导向轨道均由8组RL电路串联组成，其中导行轨参数Rst为0.11Ω，Lst为2.58μH，滑橇轨参数Rgt为28.3 mΩ，Lgt为1.1μH。

3 模型仿真与分析

3.1 多气隙击穿仿真结果

雷电击中车厢表面后，雷电流通过车体金属框架流入悬浮臂，使得各气隙两端电压迅速增大，并最终击穿气隙从而实现接地。由于导向电磁铁与轨道之间的间距大于滑橇与轨道的间距和制动电磁铁与轨道的间距，即该种气隙具有最小的击穿阈值30 kV。从仿真结果来看，有数个导向电磁铁与轨道之间的气隙被击穿，而其他2种气隙两端的电压均未达到相应的击穿阈值。这个结果说明在磁浮列车车体与轨道之间的多种气隙中，导向电磁铁与轨道之间的气隙是雷击磁浮列车的泄流路径。

根据仿真结果，在一次雷击的情况下磁浮列车出现了多处气隙被击穿的特性。雷击车体气隙泄流路径的分布结果如图4所示，由于所有滑橇和轨道形成的气隙均没有被击穿，因此图4中标示的击穿位置均指导向电磁铁与轨道形成的气隙。

图4 雷击车厢的泄流路径分布

被击穿的气隙成为雷电流的泄流通道，车体自身存在一定的阻抗，被击穿的气隙也具有一定的等效电阻，因此雷电流流过这一泄流通道时会产生压降，即形成了车体对地的电位抬升。雷击磁浮列车的过电压波形如图5所示，雷击车体过电压在很短的时间里迅速爬升至34.7 kV，且过电压由于车体的电抗成分而呈现震荡的波形。在车体遭受雷击后的1.54μs后过电压衰减至3.96 kV并逐渐减小，这个时间与气隙承受高压被击穿的时间近似，这是由于被击穿的气隙为雷电流提供了低阻通道，使得车体电位迅速降低。

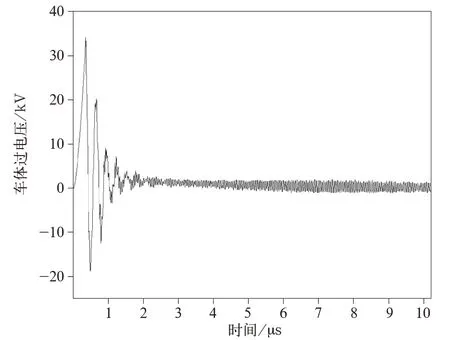
图5 雷击车体过电压波形

3.2 多气隙击穿的影响因素分析

雷电流从车体到大地的流通路径包括车厢、车厢与悬浮臂的连接线、导向电磁铁与轨道的气隙和轨道。在单节车体中相邻2条气隙的等效电路如图6所示，其中假定已有一条气隙被击穿，该气隙阻抗特性为一个10 mΩ的电阻r，另一条气隙的阻抗特性仍为0.148 nF电容CFM。

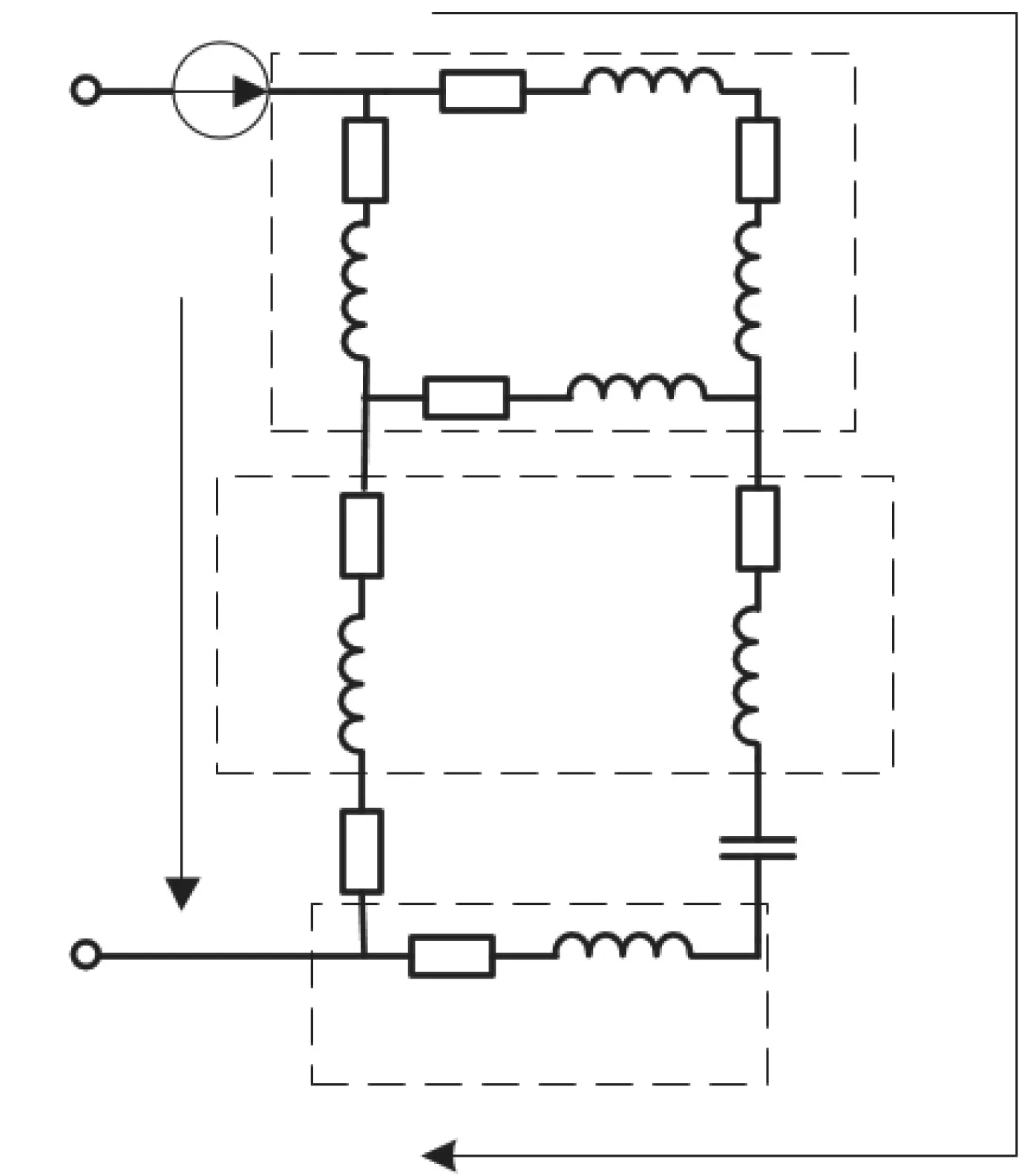
图6 相邻接地路径等效电路

由于车厢阻抗较小，为简化分析，将车厢阻抗视为等电位体，图6简化后其电流支路1和电流支路2为并联结构，故2条支路2端的电压相等，根据基尔霍夫定律，这个等效电路中的电容CFM的电压uC为式（6）：

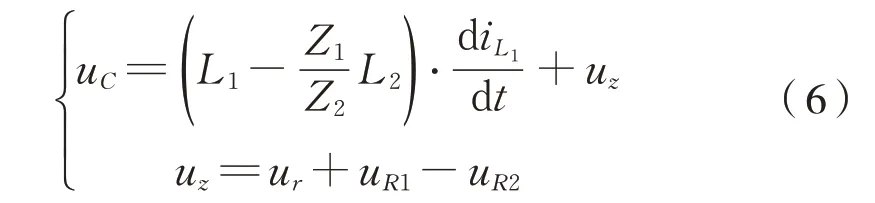
式中：L1和L2分别表示支路1和支路2的总等效电感；Z1为支路1的总等效阻抗；Z2为支路2的总等效阻抗；ur表示已击穿气隙的电压；u R1和uR2分别表示支路1和支路2的总等效电阻电压；iL1为支路1的电流。

从式（6）可以分析得出直击雷作用在磁浮列车车体时出现的多点气隙击穿泄流的原因。由于10/350μs雷电流的前沿具有很大的电流变化率，故作用于电感上将形成高电压差。在电流支路1中，连接线电阻和击穿气隙的等效电阻产生的压降远远小于电感引起的压降，因此电流支路1的电压约等同于电感电压。在电流支路2中，由于电容阻抗远大于电阻和感抗，因此电流支路2的电压近似等于电容电压。由上述可得在磁浮列车已经产生1条击穿气隙的情况下，临近电流支路的气隙电压受2条支路电感差值和连接线电阻影响，其中连接线电阻带来的压降可忽略不计。

由上述分析可知，磁浮列车气隙电压受不同电流支路的电感差值和电流变化率影响，在磁浮列车遭受直击雷后，会由于车体电压上升产生气隙击穿，而在1条气隙击穿后，其他未被击穿的气隙电压将随之升高，最终达到空气击穿阈值而再次产生泄流通道。

由于车厢和轨道的制造工艺及材料属性使得其阻抗恒定，但连接线电感可由型号和使用长度的不同甚至是铺设方式的不同而改变。其中对多气隙击穿特性具有显著影响的是连接线电感，为分析不同电感值对多气隙击穿出现的难易程度，文中根据图6所示的电路仿真了在固定雷电流峰值下，不同连接线电感值对气隙电压的影响，其中已击穿气隙通道的连接线电感值为变量，仿真结果如图7所示。

图7 电感差值对气隙电容电压的影响

随着已击穿气隙通道的连接线电感值增大，未击穿气隙通道与已击穿气隙通道的电感差值也将增大。由图7可知，未击穿气隙的电容电压波形峰值随已击穿气隙通道的电感增大而呈现增大趋势，且衰减时间变得更长。当已击穿气隙通道的连接线电感超过4.67μH后，未击穿气隙的电容电压峰值即可达到气隙的击穿电压阈值30 kV，从而引起气隙的再次击穿。仿真结果解释了图4中磁浮列车多气隙泄流的分布特性，即在磁浮列车雷击泄流过程中，当首条气隙被击穿后，即使雷电流已经存在泄流通道，但由于雷电流具有高峰值、高瞬变率的特点，加之若车体连接线过长导致电感较大，仍会引起车厢后端出现其他被击穿的气隙。

4 雷电流冲击试验证明

为了验证多气隙击穿特性及其影响因素，文中搭建了一个双气隙等效试验平台。该试验件结构如图8（a）所示，试验件共有2组，每组分为3层。第1层等效为车厢。第2层是1根横向长3 m的金属板，它表征悬浮臂中的导向电磁铁。第3层的金属板被表征为轨道。第1层与第2层由1根金属导线连接，导线的电感为1.17μH，第2层和第3层之间的间距被控制在10 mm。金属板的阻抗与图6所示的气隙支路的阻抗特性一致。各层结构由绝缘体所固定。2组试验件的第1层和第3层均由金属导线等电位连接。

试验电路示意图如图8（b）所示。在第1组的第1层和第3层分别引出接线端并与电流冲击源的正负极连接，将第2层与第3层用低阻导线直接短接，以表征1条已被击穿的气隙通道。第2组不作处理。

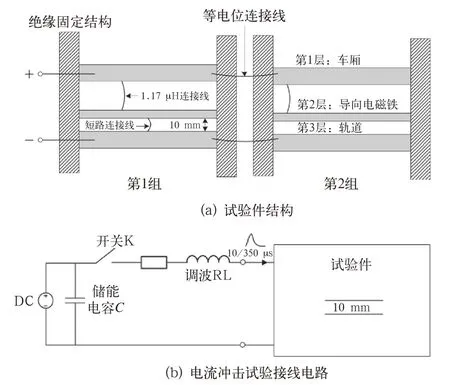
图8 电流冲击试验平台

电流冲击源输出电流波形的前沿为10μs，输出电流峰值为20 kA。将试验件第1组中的连接线电感值作为变量，以0.5μH为步进值，取0.5～5μH的范围，保持其余试验参数和试验环境不变，进行多次雷电冲击试验。采用摄像机记录第2组试验件的平板气隙，捕捉其试验结果图像。

测试得到的雷电流输出电流波形如图9所示，由于试验条件有限，文中未测试气隙被击穿时的瞬态电压波形。试验结果显示，第2组平板气隙随着第1组连接线电感值不同而呈现不同的击穿结果。在第1组的连接线电感值小于3μH时，第2组平板气隙未出现明显异常，而当连接线电感值大于3μH时，第2组平板气隙出现了明亮的火花放电现象。摄像机捕捉到的气隙击穿图像和第2组平板被击穿后的图像如图10和图11所示。第2层与第3层构成的平板电容气隙中释放出明亮的电火花并向四周溅射，如图10所示。多次重复试验后留下的气隙击穿痕迹，如图11所示，第3层金属板留下的斑点即为气隙击穿伤痕。该试验成功证明了磁浮列车多气隙击穿的特性，为进一步开展磁浮列车雷击泄流机理提供了理论支持，同时该试验验证了影响多气隙击穿的因素为气隙支路的电感值这一结论，为工程上研究磁浮列车防雷设施和布线措施提供了参考。

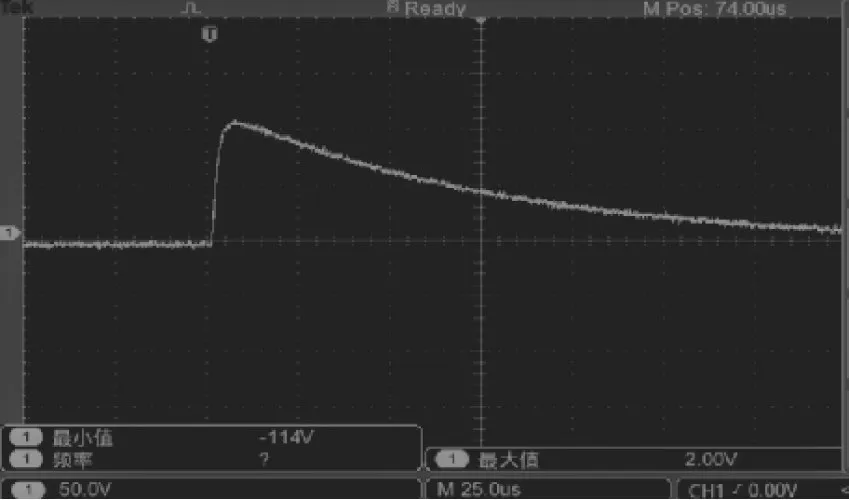
图9 实测输出电流波形

图10 气隙被击穿的瞬间

图11 气隙被击穿留下的痕迹

5 结论

主要研究了磁浮列车雷击车体情况下，导向电磁铁与轨道之间的多个气隙被高压击穿而泄流的特性，通过等效电路仿真和雷电流冲击试验2种方法进行了分析和验证，得到如下结论：

（1）导向电磁铁和轨道之间的气隙为磁浮列车的雷击泄流通道。雷电流击中磁浮列车表面后，经过车体金属框架和连接线到达悬浮臂，巨大的能量将导向电磁铁和轨道之间的气隙击穿，最终由轨道接地装置进入大地。这一过程中，雷击车体过电压峰值达到34.7 kV，当气隙被击穿后，该过电压迅速降低至3.96 kV。

（2）在雷电流泄流过程中，有多个导向电磁铁和轨道之间的气隙被击穿，多气隙击穿主要与雷电流的上升速率和各气隙支路的电感值有关。在同一节车厢中，临近位置的气隙由于支路电感值较小而不能击穿，因此多气隙击穿出现在车厢后端处。

（3）雷电流冲击试验证明了磁浮列车的多气隙击穿特性，并验证了气隙电感值为其影响因素，但由于电流冲击源型号的原因，雷电流上升速率对多气隙击穿的试验需要进一步改进仪器来证明。