高等数学课程中基于GeoGebra软件的信息化教学

李建涛

(辽宁大学 数学院，辽宁 沈阳 110036)

0 引言

高等数学，又称微积分，是现代科学的重要基础.高等数学课程是大学理工科学生最重要的数学基础课，对应的数学分析课程也是数学专业学生最重要的专业基础课之一.但是，目前高等数学课程的教学现状不容乐观.因为高等数学课程知识点多、难度大、理论抽象，所以很多教师在讲授高等数学课程时，已经认识到高等数学里面的无限序列和极限思维是一种本质上与学生上大学前使用的思维方式完全不同的数学思维.学习高等数学，需要学生从中小学时熟悉的有限运算过渡到无限运算，从初等数学到高等数学之间进行思维转换.高等数学中的分类、猜想、分析概括、抽象化、形式化的数学思维，让初入大学的学生较难理解和掌握，致使很多学生学习吃力，对高等数学产生畏惧心理，学习兴趣缺失.因此，就如何提高高等数学课程的教学质量，形成行之有效的教学方法，是目前高等数学教学改革的一个重要课题，而且已有很多高校教师对此进行了探索与实践[1-5].

高等数学的思维方式的形成是一个复杂的过程，是一种循序渐进的过程，包括数学概念的表示，形象化、概括、分类、猜想、归纳、分析、抽象化、形式化等等.例如数学概念的形象化是其中一个非常重要的步骤，通过形象化和可视化的例子，帮助学生建立高等数学的数学思维很有必要.现代科学发展日新月异，计算机技术迅猛提高，使用信息化和可视化的手段辅助教学，可以让学生更形象直观地认识数学思维未知的关联，从而更深刻地理解数学思想，提高学习兴趣.目前，已有很多教师对高等数学的可视化教学模式的改革进行了探索[6-14]，例如用Matlab、Mathematica、GeoGebra等软件进行可视化的设计模拟，将形式化的数学概念和问题形象化，树立了一个值得探索和推广的教学改革实践范例.

本文介绍基于GeoGebra软件进行的信息化教学改革的实践和相关案例分析.GeoGebra是完全免费开源的数学软件，具有强大的代数和几何功能，与专业的Matlab、Mathematica等收费软件相比，界面更友好，需要的预备知识更少，大多数教师和学生都能很快地上手使用.另外，GeoGebra更吸引人的一点是，可以通过滑动条工具进行动态演示一些数学过程，而且还可以通过着色工具和多角度连续的移动，更细致准确地展示相关的数学图像.在教学过程中使用GeoGebra软件进行教学实践暨信息化辅助教学，可以动态化地演示高等数学教材中抽象的概念和例子，与教科书中包含的静态图像不同，这种动态化的演示更形象直观地展示相关数学理论，实现了数学概念的可视化和动态演示，使学生能够直观地理解各种概念，有利于微积分思想的体现.配合GeoGebra的动态演示，可以提高学生对数列收敛性和无穷大的理解能力，如理解分割、近似替代、逼近、取极限等微积分学的主要思想，提高学生的空间想象力，有助于学生的数学思维从初级到高级的转变.

1 GeoGebra软件简介

GeoGebra软件是2002年美国亚特兰大大学数学系Markus Hohenwarter教授研发的用于教学的免费开源软件.软件的名字是由“Geometry”(几何)与“Algebra”(代数)组合而成.GeoGebra是一款动态几何软件，简单易学，不仅能画出静态的平面和立体图形，还能通过滑动条将一些数学过程动态地展示出来；并且具有强大的代数功能，可以进行各种代数运算.正如数学家Germain所说“代数不外乎符号的几何，几何不外乎图形的代数”，GeoGebra软件将代数和几何有机地结合起来，比较完美地解决了一些数学概念的可视化.目前在国内外数学教学的各个阶段，包括中小学和大学数学教学中，得到了广泛的应用.

GeoGebra软件主要有代数窗口和几何窗口，结合它的代数计算能力与几何作图能力，允许我们对高等数学里的各种数学对象进行研究与探索.例如，通过代数方程画出平面的、立体的图形，并且还可以通过使用区域着色的工具，将对应的数学对象更准确、更形象地表示出来.另一方面，GeoGebra软件中具有滑动条工具，可以动态化地演示一些数学过程，这是非常有用的.高等数学中比较难理解的就是一些极限思维，而这些极限思维通常是一种动态化的过程，例如取数列极限、定积分里的分割加细，取极限、逼近的思想.通过GeoGebra软件的滑动条工具，可以探索图像在某些特定作用下行为的可视化，例如可以设计极限、定积分等定义里的一些动态过程等.

GeoGebra软件允许几何和代数性质同时存在，在特定的空间上，实现一些动态化过程演示的可能性.例如，图像的多角度移动、数列动态逼近、极限过程等.通过观察点的逼近过程、定积分里分割加细过程等动态演示，可以激发学生的学习兴趣，对相关问题能够形成猜想，更容易理解相关的定义和性质.

2 动态辅助演示的教学案例

本节介绍在实际的教学实践中，利用GeoGebra软件进行可视化、信息化辅助教学的一些案例.这些案例涵盖了高等数学教材中主要的数学概念，通过教师在课堂上进行动态化演示以及鼓励学生课下利用GeoGebra软件自己动手对数学概念进行可视化的教学实验，促进学生对相关数学问题的理解，提高了学生的空间想象力，激发了学生的学习兴趣，从而取得了良好的教学效果.

2.1 案例一：数列极限

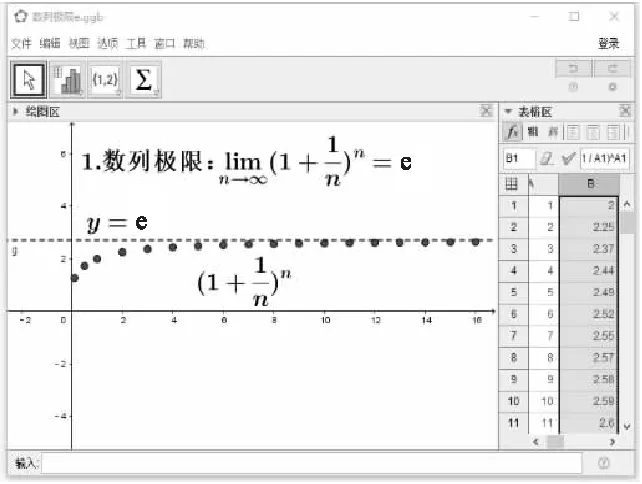
图1 数列极限

2.2 案例二：微分与导数的概念

微分和导数是高等数学中的重要概念.函数在一点处的导数的几何意义是函数对应的图像在此点处的切线斜率.通过GeoGebra软件动态演示，可以让学生形象直观地发现，切线实际上是图像上两个点确定的割线在逼近此点时的极限位置.例如图2中椭圆形的切线，实际上是该点附近的两点确定的割线在两个点逼近该点时的一个极限位置.

图2 切线的几何意义：切线与割线的关系

2.3 案例三：定积分的概念

定积分概念是微积分学中最重要的概念之一，是现代科技发展的一个重要的基础，很多平面的数学和科学问题都是通过求解定积分解决的.定积分的思想来源于这样的一个几何意义，即曲边梯形的面积.具体的过程是将曲边梯形底边分割成一些区间段，在每个区间段上用长方形近似替代曲边梯形，计算面积，最后求和，取极限，得到曲边梯形的面积，从而得到定积分的定义.使用GeoGebra软件做图，将积分区间进行分割，比较容易实现的就是均匀分割；分割之后，用每个区间段上的函数值上界确定的长方形面积代替真实的曲边梯形的面积.所以整个曲边梯形的面积近似等于这些长方形面积之和；然后将滑动条关联成分割的数目n，移动滑动条，可以形象地展示定积分的定义中加细分割和取极限的过程.随着滑动条的移动，设定的分割数目n的值变大，长方形面积之和就越来越接近真实面积.可以看到：图3曲边梯形分割成5份时，长方形面积之和还与其真实面积有较大误差.但是图4分割成30份时，长方形面积之和与其真实面积就相差很小了.通过这样的动态演示，学生完全理解了定积分这个抽象定义.

图3 定积分的定义(n=5)

图4 定积分的定义(n=30)

2.4 案例四：二重积分的概念

二重积分处理的是空间区域的相关计算，在现代科学技术中应用更加广泛.二重积分来源于这样的一个几何意义，即曲顶柱体的体积.具体的过程是首先将曲顶柱体的底部区域进行分割，分割成一些小区域，在每个小区域上用平顶的柱体近似替代曲顶柱体，计算平顶柱体的体积，最后求和，取极限，得到曲顶柱体的体积，从而得到二重积分的定义.利用GeoGebra软件，用类似定积分定义中的做法，将积分区域进行分割，比较容易实现的是分割成一些正方形的并集.将滑动条关联成分割的正方形区域的个数，移动滑动条可以增加区域分块，形象地展示二重积分里的加细分割和取极限的过程；还可以单独或者全部展示分块区域，让学生能够看到所有的细节，更加形象化；教师讲解的时候也可以单独拿出一个分块区域，讲述利用平顶柱体近似替代曲顶柱体的思想.参照下面的图5和图6.

图5 二重积分定义：单独的分块区域

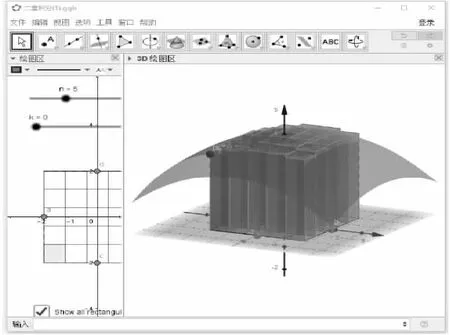
图6 二重积分定义：展示全体分块

2.5 案例五：复杂图形的可视化

高等数学教材中有很多复杂的方程和空间区域，例如心形线、马鞍面等复杂曲线和曲面，计算重积分时涉及的复杂积分区域等.空间想象力不强的学生，在学习相关内容时会十分吃力.GeoGebra软件的几何功能，既具有平面几何的功能窗口，也具有立体几何的功能窗口.利用相关的工具对这些复杂图像进行可视化，可以开发学生空间想象能力，建立空间思维，学起相关内容时更能得心应手.例如：图7给出了平面一个复杂心形线(x2+y2-1)3-x2y3=0的图像，只需要在代数区域内输入图像的代数表达式，在几何窗口就能显示图形.图8给出了高等数学教材中常见的一个积分区域：球面与圆柱面所围部分的空间区域.学生在计算重积分的时候经常弄错空间区域的上下界；单纯使用书本上的静态图像或者教师的手绘图像，即使再细致地讲解，也很难让学生理解相关区域的细节，例如投影区域、积分上下界等.然而利用GeoGebra软件的三维立体几何窗口，在代数窗口输入相关的代数方程，不仅在几何窗口可以画出这些复杂图像，还能用鼠标进行移动，让画出的区域从多个角度进行展示，例如积分区域的投影区域、积分上下界等.学生可以从各个角度观察区域的细节，并可以通过着色功能更细致准确地展示相关区域的细节.

图8 球面与圆柱面相交部分所围区域

3 结语

本文总结高等数学课程中基于GeoGebra软件的信息化教学改革方式.教学改革的目的是使用信息化手段研究高等数学中的一些数学概念和性质，理解高等数学中的极限思维；并利用GeoGebra软件对一些复杂函数进行区域着色和多角度展示，实现数学的形象化和可视化，以提高教学效果.

GeoGebra这个软件允许将代数方程和图形表示结合起来，具有十分强大的功能.而且结合最近的网络教学形式，我们发现GeoGebra这个软件更适应线上线下的混合式教学.在线上线下的混合式教学过程中，通过直播更容易展示这个强大的工具，更方便让它到达最需要的“教室”.学生可以通过直播观察到教师使用GeoGebra软件的所有细节，更方便学生学习和使用这个软件.在实际的教学实践中，学生对使用GeoGebra软件十分感兴趣，很多学生课下自己进行实验，使用这个软件进行画图，更深刻地理解了相关的数学概念和数学思想.

基于GeoGebra软件的信息化教学是非常新鲜和有效的教学手段.通过GeoGebra软件将数学概念可视化并作动态演示，有助于学生直观形象地理解数学相关概念，提高他们的观察能力和空间想象力，激发学生的学习热情，对高等数学课程的教学改革起到了积极的促进作用；课上结合相关图形进行教学，学生们也更深刻地理解了数学里的极限思维，提高了空间想象力，加快了从初等数学的有限空间平稳过渡到高等数学的广维世界.